扩展功能
文章信息
- 顾箭峰, 邬晓光, 李筠
- GU Jian-feng, WU Xiao-guang, LI Yun
- 温变影响下基于自联想神经网络的损伤检测
- Damage Detection Using AANN-based Method under Influence of Temperature Fluctuation
- 公路交通科技, 2016, Vol. 31 (4): 96-101,148
- Journal of Highway and Transportation Research and Denelopment, 2016, Vol. 31 (4): 96-101,148
- 10.3969/j.issn.1002-0268.2016.04.015
-
文章历史
- 收稿日期: 2015-07-22
2. 加拿大阿尔伯塔大学 土木与环境工程学院, 阿尔伯塔 埃德蒙顿 AB T6G 1H9;
3. 石家庄市京昆高速公路京石管理处, 河北 石家庄 050000
2. School of Civil and Environmental Engineering, University of Alberta, Edmonton Alberta AB T6G 1H9, Canada;
3. Shijiazhuang Management Office of Beijing-Shijiazhuang Section of Beijing-Kunming Expressway, Shijiazhuang Hebei 050000, China
自20世纪80年代以来,基于振动的损伤识别法已成为结构健康监测研究的热点,它们通过跟踪动力参数(如:固有频率[1, 2]、振型、阻尼比[3]、曲率模态[4]及柔度曲率[5]等)的变化来评估结构状态。然而实际桥梁结构的动力参数不仅对结构损伤敏感,同时受环境温度变化的影响[6, 7]。温度变化易使结构的真实损伤无法得到有效识别,因此消除其对损伤检测方法的不利影响尤为重要。
作为工程中最实用、易测且测量精度很高的一种模态参数[2],频率被广泛地应用为结构损伤检测方法的敏感特征,而温变使频率波动大小可达到中等程度损伤引起的变化,从而导致损伤检测结果出现误判。Xia等通过不同材质的板和梁结构模型试验结果及青马大桥和广州电视塔的现场实测数据分析表明:结构频率随温变显著变化,且与材料的弹模热力学系数基本相关[8]。Gonzalez分析瑞士某36 m单跨简支铁路桥的全年监测数据显示,年温差引起某些扭转模态频率波动最大达35%,且频率波动与温变呈非线性相关[9]。因此,剔除温变影响已成为结构损伤检测研究的热点和难点,现已提出了多元回归模型[10]等参数化方法及主成分分析[6, 11]和因子分析[12]等非参数化方法。其中参数化法通过拟合模态参数和温度间的关系式来量化温度效应,但是温度值必须可知;而非参数化法通过直接对模态参数进行降维来削弱温度效应,但不确定性较高。这些方法虽在一定程度上可削弱温度的不利影响,但往往需要复杂繁琐的公式推导,且实际桥梁结构的温度分布及温度对动力参数影响模式复杂,制约了这些方法在桥梁结构中的运用。
为寻找简单实用且较可靠的损伤检测方法,本文提出一种自联想神经网络和奇异分析相结合的新技术。以一桥梁SHM Benchmark试验结构为研究对象,考虑温变和横向温差作用,用健康结构的前十阶竖向弯曲模态频率训练AANN,以结构频率与其网络输出间的欧式距离为损伤指标来检测结构损伤,通过对存在多级损伤和噪声干扰的Benchmark结构进行损伤检测,证明该法不仅可有效地剔除温变影响,且具有较强的鲁棒性。
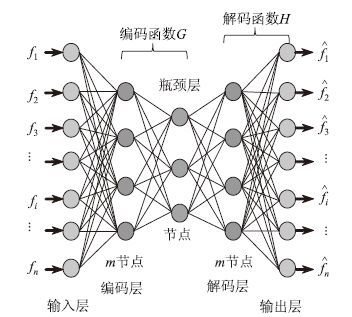
1 自联想神经网络与奇异检测 1.1 自联想神经网络自联想神经网络(AANN)常被用来解决高维空间数据的特征提取、维度缩减和模式识别等问题[13],而温变影响下基于振动的结构损伤检测本质上就属于模式识别问题,因此可用AANN来剔除温变对检测结果的影响。作为一种特殊的前馈反向传播神经网络,AANN结构如图 1所示,含输入和输出层、三个隐含层(编码层、瓶颈层和解码层),其中输入和输出完全一致。由于包含非线性激活函数隐含层的三层神经网络结构可拟合变量间的任何非线性关系[13],所以AANN结构可视为两个BPNN的集合。训练过程中,输入数据传至神经元个数较少的瓶颈层,多维输入数据中最具代表性的特征得到提取,并用来在输出层再生输入数据,可分为编码和解码两步。
|
| 图 1 自联想神经网络(AANN)结构 Fig. 1 Configuration of AANN |
首先,高维数据由输入层非线性映射到瓶颈层完成特征信息的编码,n维数据压缩至l维特征数据,在过滤冗余信息的过程时,保证较小的数据损失。假设Y为输入,X为瓶颈层的映射输出,则该过程可表达为:

其次,隐含变量X由瓶颈层通过非线性函数向量H映射到具有初始数据空间的输出层实现信息的解码,可表示为:

为实现数据损失最小化,用多组数据来训练AANN,寻求合理的G和H,使网络输出$\hat Y$以零误差逼近期望输出Y。
由此,该网络可提取输入变量与隐含变量间的非线性关系,进而重构输入变量。
因此,温度作为隐含变量,运用健康结构在不同温度条件下足够数量的频率数据f=(f1,f2,…,fn)T来训练AANN模型即可提取温度对频率的作用模式,从而可再生相同的频率数据,则网络输出$\hat f$=f。当损伤结构的频率数据输入该模型时,由于损伤的影响,网络输出和期望输出(即:原输入)间将产生显著的差异,即可指示损伤。
1.2 奇异分析技术理想状态下,利用上述过程可直观地识别结构损伤。然而,实际工程中由于测试数据固有的不确定性,仅依据输入与输出间的差异即判定结构频率波动的原因是结构损伤而非温度变化是不可靠的,且多维数据分析较复杂。因此,为从统计学上量化网络输出与期望输出间的差异,可运用多种距离度量、概率密度估计、小波分析等技术来进行奇异分析。
本文以欧式范数[14]为奇异指标来量化网络输出与期望输出间差异。当结构未知状态的频率数据f′={f′1,f′2,…,f′n}T输入一训练好的AANN时,输出 $\hat f$′={$\hat f$′1,f′2,…,f′n}T,那么奇异指标NI可由式(3)计算:
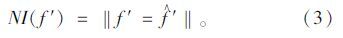
当结构仍处于健康状态时,NI(f′)的大小将趋近0;反之,一旦存在损伤,NI($\hat f$′)的大小将会显著增大,进而指示损伤。
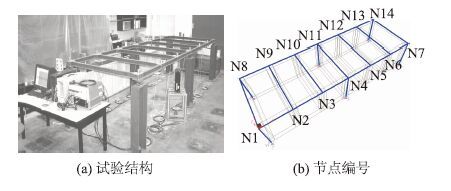
2 桥梁SHM Benchmark模型及仿真分析 2.1 桥梁SHM Benchmark结构试验为促进中小跨径桥梁结构健康监测研究的发展,中弗罗里达大学(UCF)在结构实验室建造了一个Benchmark结构模型,见图 2(a)。该两跨连续框架结构由两根长5.49 m的纵梁(S3×5.7)、7根长1.83 m的横梁(S3×5.7)和6根长1.07 m的支撑(W12×26)组成,用于模拟中小桥梁的动力和静力特性[5]。横梁均匀分布于两纵梁之间,纵横梁采用2个抗剪角钢、2块抗弯缀板和30根螺栓连接(如图 3(a),图中“HC”为“健康状态”),而梁柱间采用螺栓和圆钢来模拟实际桥梁支座,这些可更换构造使试验结构能模拟桥梁结构的多种损伤。
|
| 图 2 桥梁SHM Benchmark结构 Fig. 2 Bridge SHM Benchmark structure |

|
| 图 3 桥梁SHM Benchmark试验结构健康及两损伤工况下纵横梁连接点构造 Fig. 3 Typical details of connections of bridge SHM Benchmark structure in heathy state and 2 experimental damage scenarios |
在Benchmark试验结构中,通过卸掉纵横梁连接构造的螺栓和缀板,如图 3(b)和3(c)所示,构造了两种损伤工况(见表 1中的DC1和DC2)来模拟实际桥梁中普遍存在的局部刚度减小病害。选择图 2(b)中的2,5,6,12这4点为激振点,而在除7,14外的12个节点上布置PCB393加速度计。试验过程中,用力锤对每个激振点进行单点激振,采集各加速度测点的竖向加速度,采样频率为400 Hz,每次持续时间为10.24 s。利用复模态指示函数法识别分析加速度信号和力信号(NFFT=4 096),识别结构在健康状态和各损伤工况下的多阶竖向弯曲模态频率[15],部分频率的试验值见表 2。由这些试验数据可知,损伤会导致频率变化。
| 损伤工况 | 损伤特征 | 试验结构 | 有限元模型 | 损伤位置 |
| DC1(损伤轻微) | 横梁两端铰接 | 卸掉横梁梁端各8个螺栓 | 释放横梁两端的转动自由度 | 节点3,10 |
| DC2 (损伤较弱) | 横梁一端铰接,削弱梁局部的抗弯刚度 | 卸掉缀板和连接螺栓 | 释放横梁一端转动自由度,交点处梁单元均替换成S3×5.7截面 | 节点3 |
| DC3 (损伤适中) | 横梁两端铰接,削弱梁局部的抗弯刚度 | 无 | 释放横梁两端转动自由度,交点处梁单元均替换成S3×5.7截面 | 节点3,10 |
| DC4 (损伤严重) | 横梁两端铰接,削弱梁局部的抗弯刚度 | 无 | 释放横梁两端转动自由度,交点处梁单元均替换成S3×5.7截面 | 节点3,10,5,12 |
为分析温变对Benchmark结构频率的影响,建立了如图 4(a)所示的有限元模型,通过释放梁端的转动自由度和减小梁顶底板厚度来模拟结构损伤,计算参考温度(15 ℃)下其前十阶竖向弯曲模态频率。由表 2中列出的其中三阶频率计算值可知,该有限元模型可较准确地模拟Benchmark试验结构的动力特性。

|
| 图 4 Benchmark结构有限元模型温度分布及钢材的材料属性 Fig. 4 Temperature distribution in FE model of Benchmark structure and material characteristic of steel |
| 工况 | 一阶频率/Hz | 六阶频率/Hz | 九阶频率/Hz | |||||||||||||
| 参考温度下 | 考虑温变影响 | 参考温度下 | 考虑温变影响 | 参考温度下 | 考虑温变影响 | |||||||||||
| 试验值 | 计算值 | 最小值 | 最大值 | 变化率/% | 试验值 | 计算值 | 最小值 | 最大值 | 变化率/% | 试验值 | 计算值 | 最小值 | 最大值 | 变化率/% | ||
| HC | 22.37 | 21.89 | 21.55 | 22.37 | 3.7 | 67.27 | 67.02 | 65.98 | 68.49 | 3.8 | 103.58 | 102.03 | 100.45 | 104.28 | 3.8 | |
| DC1 | 22.38 | 21.89 | 21.55 | 22.37 | 3.7 | 67.01 | 66.85 | 65.81 | 68.32 | 3.8 | 103.54 | 102.02 | 100.43 | 104.29 | 3.8 | |
| DC2 | 22.40 | 21.82 | 21.48 | 22.30 | 3.8 | 67.37 | 66.79 | 65.75 | 68.25 | 3.7 | 104.00 | 101.79 | 100.20 | 104.05 | 3.8 | |
| DC3 | — | 21.75 | 21.41 | 22.22 | 3.7 | — | 66.60 | 65.56 | 68.05 | 3.7 | — | 101.49 | 99.92 | 103.73 | 3.7 | |
| DC4 | — | 21.60 | 21.26 | 22.07 | 3.7 | — | 66.03 | 65.00 | 67.48 | 3.7 | — | 100.97 | 99.40 | 103.21 | 3.8 | |
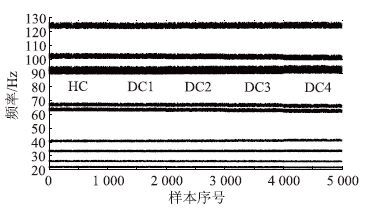
实际桥梁结构监测需考虑温度变化影响,且应考虑结构的横向温差。因此,在有限元模型中,假定温度分布如图 4(a)和4(b)所示,其中T1,T2值在-15~50 ℃范围内变化,且两者间最大差值 为20 ℃。为考虑材料非线性,钢的弹性模量随温度变化如图 4(c)所示[16],同时把结构温度与参考温度的差值作为温度荷载施加在相应构件上。为说明温变对损伤检测的影响,在数值模型中仿真模拟表 1中的4个逐级加重的损伤工况(DC1~DC4)。建立结构在健康和各损伤工况下的1 000种不同温度分布的数值模型,计算各模型的前十阶竖向弯曲模态频率。计算结果如图 5所示,在温变条件下,Benchmark结构的每阶频率在同一工况中均产生较大波动,且不同工况的频率分布范围几乎一致,使得结构状态难以识别。
|
| 图 5 Benchmark结构健康和各损伤工况的前十阶频率分布 Fig. 5 Distribution of the first 10 frequencies of Benchmark structure in healthy state and all damage states |
表 2为各工况下Benchmark结构的三阶竖向弯曲模态频率随温变的波动情况。表中数据表明:温变条件下,结构在各工况下的各阶频率变化率(即:频率最大值和最小值之差与其均值的比值)均较大,且各损伤工况和健康工况结构的每一阶频率值均交叉,难以判断具体频率值对应的结构状态。因此,温变引起的Benchmark结构频率波动湮没了结构损伤导致的频率变化。
3 温变影响下损伤识别以桥梁SHM Benchmark结构健康工况的前十阶竖向弯曲模态频率为损伤敏感特征来构造AANN模型,则网络输入和输出层均含10个节点;而温度为导致频率波动的唯一潜在因素,则瓶颈层只有1个节点。为避免过拟合和欠拟合问题,采用试误法来确定网络编码和解码层的节点数m。m在2~14范围内变化进行逐一试验,对比分析结构健康工况频率的重构误差,误差值在m=4时最小。因此泛化能力最优的AANN模型10-4-1-4-10,其3个隐含层的激活函数均为tansig,而输出层模型激活函数为pureline。
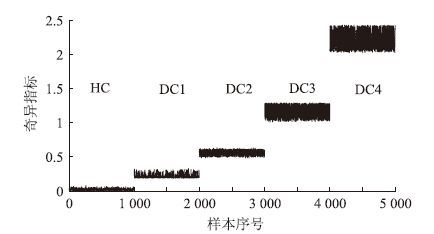
3.1 有效性分析以Benchmark结构健康工况的频率数据为训练集训练得最优的AANN模型,用4个损伤工况的频率为测试集输入该模型,计算各工况的奇异指标(NI)序列如图 6所示。图 6显示各工况NI值变化范围区分明显,并呈递增趋势,则该方法可定性识别结构损伤程度的大小;且即使是微小损伤工况DC 1的NI值,也能有效地与健康工况HC的NI值区分。表 3统计分析结构各工况的奇异指标,各损伤工况的NI均值均远大于HC的相应值,它们相对HC的均值变化率rm值由851.8%递增至9 763.5%,可很容易地准确判断结构是否存在损伤,且其值明显随着损伤程度加剧而递增,再一次验证了图 6得到的结论。因此,本文方法不仅可有效地剔除温变对损伤检测结果的不利影响,能可靠地检测温变条件下结构损伤的存在,且能定性区分结构的损伤程度。
|
| 图 6 温变条件下Benchmark结构健康和各损伤工况的奇异指标序列 Fig. 6 Novelty index sequences for Benchmark structure in healthy state and all damage cases under temperature fluctuation |
| 奇异指标 NI | 平均值/(×10-2) | 标准差/(×10-2) | 均值相对变化率rm/% | 标准差相对变化率rs/% |
| HC | 2.236 | 1.41 | — | — |
| DC1 | 21.286 | 2.84 | 851.8 | 101.5 |
| DC2 | 55.797 | 4.21 | 2 394.9 | 198.3 |
| DC3 | 115.760 | 9.30 | 5 076.1 | 559.1 |
| DC4 | 220.591 | 13.79 | 9 763.5 | 877.2 |
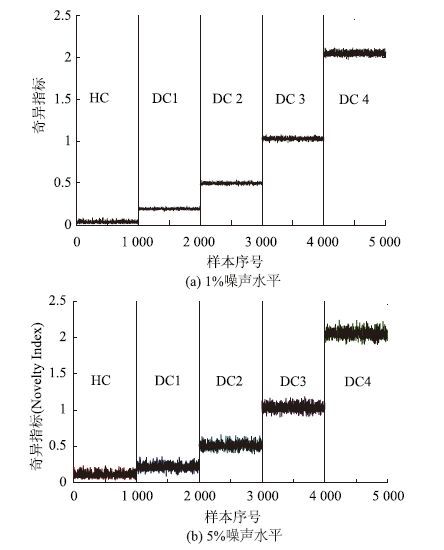
噪声干扰在工程中不可避免地存在[6],且能显著降低损伤检测方法的可靠性,它的存在不仅会导致轻微结构损伤无法检测,且易使健康结构得到误判。为分析本文检测方法的噪声鲁棒性,对各结构工况的频率数据加入高斯白噪声以模拟噪声的干扰,计算它们在不同噪声水平(噪信比为1%~5%)下的NI值。1%和5%噪声水平下的计算结果如图 7(a)和7(b)所示,且表 4对它们进行了统计分析。
|
| 图 7 基于噪声干扰数据的温变条件下健康和各损伤状态 Benchmark结构的奇异指标序列< Fig. 7 Novelty index sequences for Benchmark structure in healthy state and all damage cases under temperature fluctuation based on noisy data |
| 奇异指标NI | 平均值/(×10-2) | 均值相对变化率rm/% | ||
| 1% | 5% | 1% | 5% | |
| HC | 3.274 | 11.306 | — | — |
| DC1 | 19.153 | 21.817 | 485.1 | 93.0 |
| DC2 | 49.719 | 51.138 | 1 418.7 | 352.3 |
| DC3 | 103.013 | 103.698 | 3 046.6 | 817.2 |
| DC4 | 204.839 | 205.452 | 6 157.0 | 1 717.2 |
图 7直观地表明,在不同水平的噪声干扰下,Benchmark结构各损伤工况的NI序列相对于健康工况均明显增大,且它们仍然随损伤程度的加重而递增。由表 4可知,1%和5%的噪声水平下,健康结构的NI均值分别为0.033和0.113,而各损伤工况的均值分别在0.192~2.048和0.218~2.054范围内逐级增大,它们相对健康工况的相对变化率rm分别在485.1%~6 157%和93%~1 717.2%内递增。虽然这些数值相对于表 3中数据明显减小,但仍能有效判断损伤的存在和定性判别损伤程度的大小。因此,本文损伤检测法具有较强的噪声鲁棒性。
4 结论本文为剔除温变对结构损伤检测结果的不利影响,提出了一种结合AANN和奇异分析技术的检测方法。以温变影响下结构的模态频率为损伤敏感特征,首先用健康状态结构的频率数据训练AANN,然后输入未知状态下结构的频率数据,构造网络输出与期望输出间的欧式距离并将其作为损伤识别指标来检测结构损伤。通过仿真分析UCF桥梁SHM Benchmark试验结构模型来验证该法的有效性和鲁棒性,得到如下结论:
(1)这种方法不仅可有效地检测温变影响下结构损伤的存在,且可定性地区分损伤程度的大小。
(2)该法具有较强的噪声鲁棒性,在5%的噪声水平下,仍能准确检测结构损伤的存在及定性判别损伤程度。
(3)通过奇异分析技术把多阶频率数据的多元分析问题转化为奇异指标的一元分析,可显著提高该法的检测效率。
(4)该法基于工程中最简单实用且测试精度高的结构频率数据,而且属于无监督学习,仅需健康结构的频率数据训练网络,可为实际桥梁结构的在线监测提供参考。
| [1] | 孙红跃,董峰. 基于神经网络的建筑结构损伤识别方法[J]. 控制工程,2015,22(2): 287-290. SUN Hong-yue, DONG Feng. Damage Identification of Building Structural Based on Neural Network[J]. Control Engineering of China, 2015, 22(2): 287-290. |
| [2] | 韩东颖,时培明. 基于频率和BP神经网络的井架钢结构损伤识别[J]. 中国安全科学学报,2012,22(8): 118-123. HAN Dong-ying, SHI Pei-ming. Identification of Derrick Steel Structures Damage Based on Frequency and BP Neural Network[J]. China Safety Science Journal, 2012, 22(8): 118-123. |
| [3] | 黄晓敏,韩晓健,顾大鹏. 基于阻尼特性的RC桥梁损伤识别方法[J]. 公路交通科技,2012,29(11): 63-68, 79. HUANG Xiao-min, HAN Xiao-jian, GU Da-peng. Damage Detection of RC Bridge Based on Damping Characteristics[J]. Journal of Highway and Transportation Research and Development, 2012, 29(11): 63-68, 79. |
| [4] | 宋子收,周奎,李胡生,等. 基于曲率模态和小波系数差的损伤识别[J]. 公路交通科技,2010,27(11): 61-66. SONG Zi-shou, ZHOU Kui, LI Hu-sheng, et al. Damage Identification Based on Curvature Mode and Difference of Wavelet Coefficients[J]. Journal of Highway and Transportation Research and Development, 2010, 27(11): 61-66. |
| [5] | CATBAS F N, GUL M, BURKETT J L. Damage Assessment Using Flexibility and Flexibility-Based Curvature for Structural Health Monitoring[J]. |
| [6] | 吴森,韦灼彬. 基于主成分残差的结构损伤识别方法[J]. 公路交通科技,2011,28(7): 113-117, 130. WU Sen, WEI Zhuo-bin. Structure Damage Identification Based on Residual Error of Principal Component[J]. Journal of Highway and Transportation Research and Development, 2011, 28(7): 113-117, 130. |
| [7] | 梁亚斌,李东升,李宏男. 环境温度影响下基于频率协整的在线损伤识别[J]. 大连理工大学学报,2014,54(3): 307-314. LIANG Ya-bin, LI Dong-sheng, LI Hong-nan. Online Damage Detection Based on Cointegration of Frequencies under Influence of Environmental Temperature[J]. Journal of Dalian University of Technology, 2014, 54(3): 307-314. |
| [8] | XIA Yong, CHEN Bo, WENG Shun, et al. Temperature Effect on Vibration Properties of Civil Structures: A Literature Review and Case Studies[J]. |
| [9] | GONZALEZ I. Application of Monitoring to Dynamic Characterization and Damage Detection in Bridges[D]. Stockholm, Sweden: KTH Royal Institute of Technology, 2014. |
| [10] | ZHOU G D, YI T H. A Summary Review of Correlations between Temperatures and Vibration Properties of Long-span Bridges[J]. Mathematical Problems in Engineering, 2014, Article ID 638209: 19. |
| [11] | 孙晓丹,欧进萍. 基于小波包和概率主成份分析的损伤识别[J]. 工程力学,2011,28(2): 12-17. SUN Xiao-dan, OU Jin-ping. Structural Damage Identification Based on Wavelet Packet Energy and PPCA[J]. Engineering Mechanics, 2011, 28(2): 12-17. |
| [12] | 吴森,韦灼彬. 基于小波包能量谱和因子分析的结构损伤识别方法[J]. 解放军理工大学学报:自然科学版,2011,12(5): 12-17. WU Sen, WEI Zhuo-bin. Method of Structural Damage Identification Based on Wavelet Packet Energy Spectrum and Factor Analysis[J]. Journal of PLA University of Science and Technology: Natural Science Edition, 2011, 12(5): 12-17. |
| [13] | KRAMER M A. Nonlinear Principal Component Analysis Using Autoassociative Neural Networks[J]. |
| [14] | 王修勇,温青,杨琪,等. 基于新奇检测技术的斜拉索状态评估[J]. 公路交通科技,2011,28(9): 53-59, 118. WANG Xiu-yong, WEN Qing, YANG Qi, et al. Condition Assessment for Stay Cables of Cable-stayed Bridge Based on Novelty Detection Technique[J]. Journal of Highway and Transportation Research and Development, 2011, 28(9): 53-59, 118. |
| [15] | GUL M. Investigation of Damage Detection Methodologies for Structural Health Monitoring[D]. Orlando, Florida: University of Central Florida, 2009. |
| [16] | YAN A M, KERSCHEN G, BOE P D, et al. Structural Damage Diagnosis under Varying Environmental Conditions—Part I: A Linear Analysis[J]. |
 2016, Vol. 31
2016, Vol. 31
