扩展功能
文章信息
- 江楠, 邓扬, 刘扬, 张海萍, 李明
- JIANG Nan, DENG Yang, LIU Yang, ZHANG Hai-ping, LI Ming
- 持续荷载与腐蚀共同作用下RC梁的抗弯刚度计算方法
- A Calculation Method of Flexural Stiffness of RC Beam under Sustained Load Coupled with Corrosion
- 公路交通科技, 2016, Vol. 31 (4): 66-72
- Journal of Highway and Transportation Research and Denelopment, 2016, Vol. 31 (4): 66-72
- 10.3969/j.issn.1002-0268.2016.04.011
-
文章历史
- 收稿日期: 2015-03-19
钢筋锈蚀已成为影响结构耐久性的最主要因素之一。在实际工程中,变形是衡量结构构件使用性能的重要指标,因此钢筋锈蚀对构件抗弯刚度的影响是研究混凝土结构耐久性的关键问题[1]。目前,国内外研究者就导致RC梁抗弯刚度退化的因素已基本达成共识[2, 3],其原因主要分为以下3个方面:(1)钢筋截面积的减少;(2)材料性能的劣化;(3)钢筋与混凝土间黏结性能的退化。其中,对于黏结性能的退化还存在较大差异,以往的研究通常使用无锈蚀构件的刚度计算公式乘以协同工作降低系数来体现黏结性能的退化,且之前的试验研究大多数是对不受荷载作用的试件施加电流来加速钢筋的锈蚀,然后对试件锈蚀后的性能进行研究[4, 5, 6, 7],一些学者虽然研究了荷载与腐蚀共同作用对RC梁力学性能的影响,但其腐蚀区域仅为纯弯段[8, 9, 10, 11],这与实际状况并不完全相符。在实际工程中,锈蚀是在结构承受荷载的过程中发生的,且在我国超载现象普遍存在[12],超载运营对于桥梁结构的承载性能和耐久性都有着不可忽视的劣化影响[13, 14, 15],因此研究荷载与氯离子侵蚀复合作用对桥梁结构的影响具有现实意义。
本研究进行了5组钢筋混凝土梁的试验(分别为参考组、无荷载作用组、正常使用状态、超载一级、超载二级),通过施加持续荷载和通电加速腐蚀,模拟了正常使用状态及超载状态与腐蚀共同作用对RC梁力学性能的影响,从试验结果入手,总结出持续荷载等级对钢筋锈蚀率影响规律,并结合抗弯试验结果,探讨了考虑不同位置处钢筋锈蚀的抗弯刚度计算方法。
1 试验概况试验中采用电化学方法来实现梁内受拉钢筋的快速锈蚀。将梁体浸入浓度为5%的NaCl溶液中,钢筋作为阳极,不锈钢板作为阴极,连通电源,通过NaCl溶液形成闭合回路,在电流的作用下,受拉钢筋发生锈蚀。梁的计算跨径为1 800 mm。配筋布置如图 1所示。

|
| 图 1 试验梁截面尺寸及配筋(单位:mm) Fig. 1 Cross-sectional dimensions and reinforcement of test beam (unit: mm) |
试验中12片RC梁受拉钢筋均为螺纹钢筋,混凝土采用硅酸盐水泥,设计强度为C40。首先,通过对参考梁进行抗弯极限承载力试验,确定RC梁的抗弯极限荷载,并依据规范中对挠度限值的规定确定超载界限,加载装置如图 2所示;然后,在腐蚀过程中,通过千斤顶对试验梁进行加载以此来模拟持续荷载,荷载水平分为三级,分别为极限荷载(214.35 kN)的50%,65%,80%。荷载大小通过传感器和测力仪来控制。试验梁明细如表 1所示。

|
| 图 2 试验加载装置 Fig. 2 Loading device of test |
| 梁编号 | 荷载等级/% | 加载时长/d | 备注 |
| R1 | — | — | 参考梁 |
| R2 | — | — | 参考梁 |
| CL00-10-1 | — | — | 锈蚀梁 |
| CL00-10-2 | — | — | 锈蚀梁 |
| CL50-10-1 | 50(正常使用) | 10 | 锈蚀梁 |
| CL50-10-2 | 50(正常使用) | 10 | 锈蚀梁 |
| CL65-10-1 | 65(超载Ⅰ级) | 10 | 锈蚀梁 |
| CL65-10-2 | 65(超载Ⅰ级) | 10 | 锈蚀梁 |
| CL80-10-1 | 80(超载Ⅱ级) | 10 | 锈蚀梁 |
| CL80-10-2 | 80(超载Ⅱ级) | 10 | 锈蚀梁 |
| CL80-15-1 | 80(超载Ⅱ级) | 15 | 锈蚀梁 |
| CL80-15-2 | 80(超载Ⅱ级) | 15 | 锈蚀梁 |
| 注:表中C为锈蚀梁(Corroded beam),R为参考梁(Reference beam),L为荷载(Loading),L后面的数字表示持续荷载水平(50%,65%,80%的极限荷载),“-”后面的数字表示腐蚀时间(10 d,15 d),锈蚀时间后“-”后面的数字表示每组试件的编号。 | |||
在完成RC梁的锈蚀试验后,开展锈蚀梁的剩余承载力试验。本文定义平均锈蚀率为纵向受拉筋锈蚀前后质量的减少率。试验梁加载至破坏之后,将纵筋切割成200 mm的小段并标注其所属区段,取各小段的平均值作为不同区段(纯弯段、剪弯段)钢筋的锈蚀率。锈蚀率由式(1)计算:
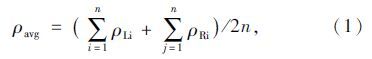
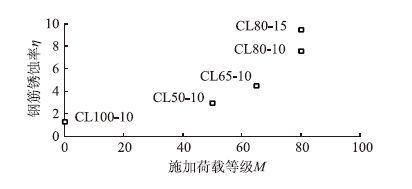
图 3给出了不同工况下RC梁锈蚀率的均值,从中可以看出,持续荷载作用下梁的钢筋锈蚀率要比无荷载作用梁的钢筋锈蚀率大,且受拉钢筋的锈蚀率随荷载等级的升高而增加,说明持续荷载加剧了受拉纵筋钢筋的锈蚀。此外,腐蚀时间相同,荷载作用大的梁锈蚀率也大。钢筋锈蚀速度随荷载等级升高而增大的原因为:(1)受拉区混凝土在拉应力作用下,密实性降低,氯离子的渗透性增强;(2)受拉区混凝土在弯曲荷载作用下达到极限拉应变后,混凝土开裂,且横向裂缝的宽度随弯曲荷载等级的升高而增大;(3)受拉区混凝土出现多条横向裂缝,并在腐蚀过程中保持张开状态,试验过程中发现,锈蚀产物多集中在横向裂缝混凝土表面。上述因素使得受拉区混凝土的渗透性增强,且钢筋的锈蚀程度随弯曲荷载等级的升高而加剧。
|
| 图 3 持续荷载对锈蚀率的影响(单位:%) Fig. 3 Influence of sustained loading on corrosion rate (unit:%) |
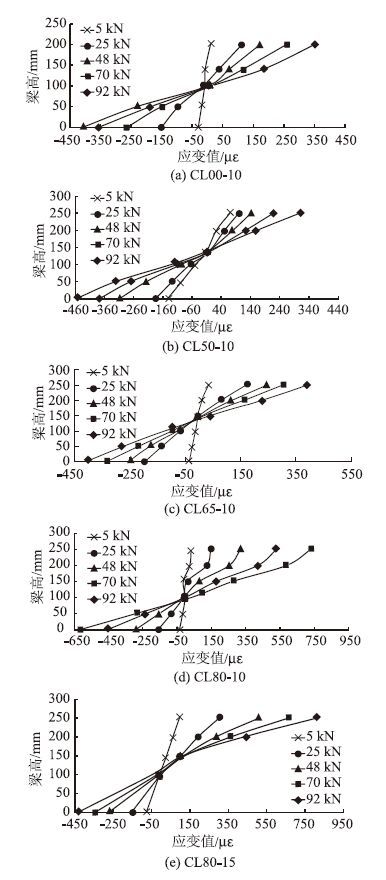
图 4给出了加速锈蚀后RC梁在不同荷载等级下跨中混凝土应变沿梁高的分布曲线。图为每组构件的平均值。观察图 4可以发现,混凝土应变变化呈线性增长,且随着施加持续荷载等级的增加,受压区应变随之减小,应变曲线斜率逐渐降低,但混凝土压应变与拉应变基本成比例增加。这说明钢筋混凝土梁在荷载与氯离子侵蚀共同作用后,混凝土的应变仍服从平截面假定。已有研究表明[16, 17, 18]:当锈蚀率较小时,钢筋应变与同位置的混凝土应变较为接近;但锈蚀率越大,钢筋与混凝土的应变不协调程度越高,混凝土与钢筋间的变形协调将不再成立。而本试验中钢筋的锈蚀率较小(<10%),因此笔者仍认为平截面假定依然适用于本试验中的RC梁。
|
| 图 4 混凝土应变分布曲线 Fig. 4 Strain distribution curves of concrete |
钢筋锈蚀后,由于锈蚀产物不断累积,致使钢筋应变与其周围的混凝土应变间的变形协调关系发生改变,钢筋应变滞后于混凝土应变,且滞后程度随锈蚀程度变化。因此定义钢筋与混凝土应变协调函数:

文献[19]通过试验,给出了不同位置钢筋应变与混凝土应变随锈蚀率的变化,拟合公式为:

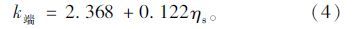
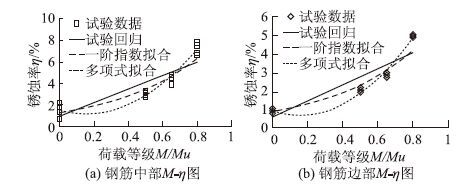
由2.1节可知,锈蚀率随荷载等级的增加而增加,因此将不同荷载作用下钢筋混凝土梁的锈蚀率与施加的持续荷载绘制成散点见图5,并通过线性、多项式、指数增长等方式对试验数据进行拟合回归,找到锈蚀率η与施加的持续荷载M的最佳拟合公式,通过对结果和相关系数的比较,选取最优的回归结果。
|
| 图 5 M-η的关系 Fig. 5 Relation between M and η |
(1)线性回归方程:
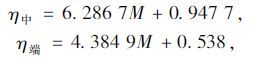
(2)多项式回归方程为:
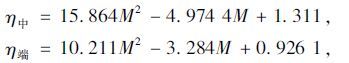
(3)指数增长形式拟合,回归方程为:
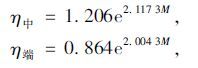
通过比较拟合程度指标R发现,多项式拟合曲线与试验数据最为吻合,即拟合结果最为理想,因此采用抛物线拟合作为荷载与锈蚀率的关系表达式。
将所得回归公式代入式(3)~(4)可以得到荷载与钢筋和混凝土应变不协调系数的关系:
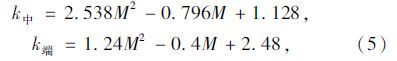
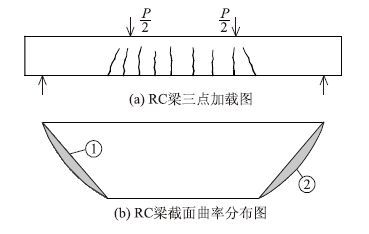
以往的研究为了简化计算,多针对于RC梁中部区域,对端部的刚度研究较少。钢筋截面曲率分布如图 6所示。钢筋锈蚀后,斜裂缝出现较早,较多,斜裂缝的不利影响较大,在以往计算抗弯刚度时采用的截面曲率为图 6(b)中标号为①的曲线,而考虑端部锈蚀影响后的曲率为标号②的曲线,因此在计算截面曲率时,以往的方法忽略了图中阴影部分的面积,造成刚度计算结果偏高。为了使计算结果更加精确,需要考虑端部区域对跨中挠度的贡献。
|
| 图 6 RC梁截面曲率分布 Fig. 6 Distribution of cross-sectional curvatures of RC beams |
剪力作用下简支梁跨中的挠度可以表示为:
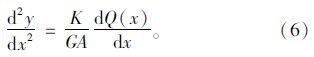
考察简支梁在对称荷载作用下的情况,则对任意截面而言,剪力如下:

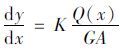 ,则
,则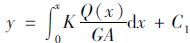 ,代入边界条件可得,y=$\frac{{KPx}}{{3GA}}$。其中,K为应力不均匀系数,此处取值为1,因此对于跨中而言,y=$\frac{{KPl}}{{3GA}}$。由弯曲变形引起的跨中挠度为y=$\frac{{6.81P{l^3}}}{{384El}}$,则剪切变形与弯曲变形引起的挠度之比为0.04,即剪弯段刚度的贡献约占全梁刚度的4%。
,代入边界条件可得,y=$\frac{{KPx}}{{3GA}}$。其中,K为应力不均匀系数,此处取值为1,因此对于跨中而言,y=$\frac{{KPl}}{{3GA}}$。由弯曲变形引起的跨中挠度为y=$\frac{{6.81P{l^3}}}{{384El}}$,则剪切变形与弯曲变形引起的挠度之比为0.04,即剪弯段刚度的贡献约占全梁刚度的4%。
锈蚀钢筋混凝土梁刚度分析采用以下假定:(1)混凝土应变满足平截面假定;(2)受拉钢筋应变滞后于同位置处的混凝土应变,不满足符合平截面假定;(3)不考虑受拉区混凝土的抗拉能力。
根据材料力学,截面抗弯刚度可以表示为:

根据几何方程、本构方程及平衡方程来确定截面曲率,如图 7所示。
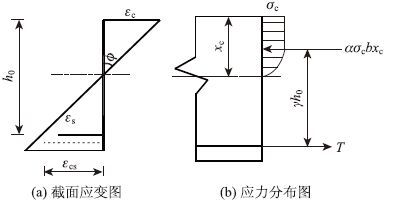
|
| 图 7 计算简图 Fig. 7 Simplified calculation diagrams |
(1)几何方程
根据图 8(a),截面曲率可表示为:

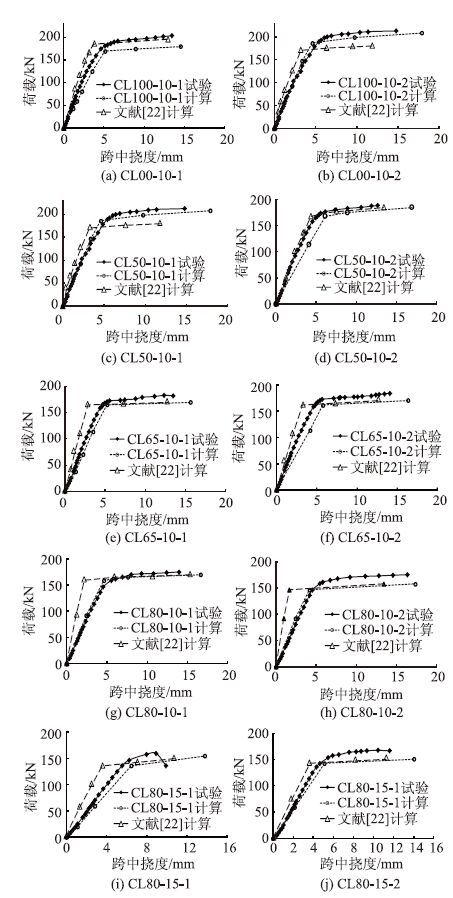
|
| 图 8 计算曲线与试验曲线对比 Fig. 8 Comparison of calculated curves with test curves |
联立式(2)与式(9),则截面曲率可以表示为:
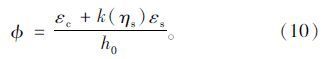
根据文献[20]的研究成果,钢筋的不均匀系数可以通过钢筋黏结系数βE来进行修正,即:
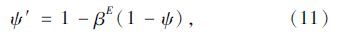
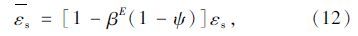
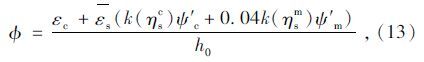
(2)本构关系
在荷载作用下,钢筋混凝土梁受压区应力分布[21]如图 7所示。混凝土压应变和纵向钢筋应变为:


(3)平衡方程
忽略受拉区混凝土的抗拉能力,根据受力平衡可以建立方程:
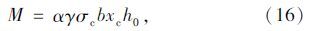

联立式(14)~(17)并代入式(13):
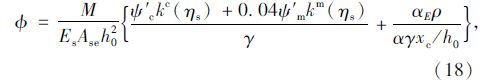
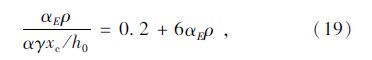
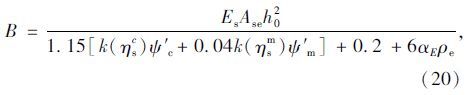
应用上述分析模型对锈蚀钢筋混凝土试件在集中荷载作用下抗弯性能进行了理论计算。跨中截面荷载与跨中挠度曲线的计算结果与试验结果的对比情况如图 8所示。当施加荷载等级较小时,由于横向裂缝的存在,受拉钢筋还是会同时出现均匀锈蚀与局部锈蚀两种状态,虽然锈坑数目较多,但锈蚀深度较浅,将截面锈蚀率转化为区段锈蚀率并代入计算仍能保持较好精度。由此可以得出结论,当锈蚀率较低,且坑蚀状况不明显时,在进行抗弯刚度计算时,可以忽略局部锈蚀的影响,以均匀锈蚀计算为依据。此外还与文献[23]的计算方法进行了对比。从图 8可以看出:锈蚀构件按本文模型计算得到的荷载-跨中挠度曲线与试验所得曲线吻合相对较好,变化趋势相当。而按照文献[23]中建议刚度计算方法得到的挠度曲线,尽管在计算跨中截面换算惯性矩时,忽略了锈蚀后纵向受拉钢筋对截面刚度的贡献,但由于没有考虑端部锈蚀的影响,刚度计算结果仍然相对偏大。因此在对锈蚀后RC梁抗弯刚度进行计算时,需要考虑不同位置处锈蚀状况对于抗弯刚度的影响。
4 结论(1)通过12片室内快速锈蚀的钢筋混凝土矩形截面梁的抗弯试验,得到不同荷载等级下纵向钢筋的锈蚀率及锈蚀钢筋混凝土矩形截面梁抗弯刚度的变化规律;通过回归分析,得出了荷载等级与螺纹钢筋锈蚀率的关系。
(2)考虑了不同位置锈蚀对RC梁抗弯刚度的影响,通过构造几何关系,得出了锈蚀钢筋混凝土矩形截面梁截面曲率的表达式,结合荷载等级对钢筋锈蚀率及钢筋不均匀系数的影响,得出持续荷载与氯离子侵蚀复合作用下RC梁抗弯刚度的计算方法,并结合试验数据对公式进行验证。
(3)锈蚀构件按本文模型计算得到的荷载-跨中挠度曲线与试验所得曲线吻合相对较好,变化趋势相当。但由于应变数据来源于以往的试验,本文中得到的钢筋应变与钢筋位置处混凝土的应变关系有一定的局限性,是否普遍适用于实际工程还值得探讨;在持续荷载作用下钢筋的锈蚀机理尚不明确,因此对于锈蚀钢筋混凝土构件不同荷载作用下锈蚀的发展仍有待进一步研究。
| [1] | 袁迎曙,贾福萍,蔡跃. 锈蚀钢筋混凝土梁的结构性能退化模型[J]. 土木工程学报,2001,34(3):47-52,96. YUAN Ying-shu, JIA Fu-ping, CAI Yue. The Structural Behavior Deterioration Model for Corroded Reinforced Concrete Beams[J]. China Civil Engineering Journal,2001,34(3):47-52,96. |
| [2] | LI C Q, ZHENG J J. Propagation of Reinforcement Corrosion in Concrete and its Effects on Structural Deterioration[J]. |
| [3] | 孙彬,牛荻涛,王庆霖.锈蚀钢筋混凝土梁抗弯刚度分析与计算[J]. 建筑结构,2004,34(10): 42-45. SUN Bin, NIU Di-tao, WANG Qing-lin. Analysis and Calculation of Flexural Stiffness of Corroded Reinforced Concrete Beam[J]. Building Structure, 2004,34(10): 42-45. |
| [4] | 王晓刚,顾祥林,张伟平.碳纤维布加固锈蚀钢筋混凝土梁的抗弯刚度[J].建筑结构学报,2009,30(5):169-176. WANG Xiao-gang, GU Xiang-lin, ZHANG Wei-ping. Flexural Stiffness of Corroded Reinforced Concrete Beams Strengthened with Carbon Fiber Composite Sheets[J]. Journal of Building Structures,2009,30(5):169-176. |
| [5] | 吕毅刚,张建仁,彭晖,等.既有钢筋混凝土л梁正截面抗弯承载力研究[J].中南大学学报:自然科学版,2011,42(2):456-462. LV Yi-gang, ZHANG Jian-ren, PENG Hui, et al. Flexural Bearing Capacity of Existing Reinforced Concrete л Beams[J]. Journal of Central South University:Science and Technology Edition, 2011,42(2): 456-462. |
| [6] | 贺拴海,吕颖钊. 考虑材料耐久性的在役混凝土结构可靠度研究[J]. 建筑科学与工程学报,2005,22(1): 71-75. HE Shuan-hai, LV Ying-zhao. Reliability Research of Existing Reinforced Concrete Structures[J]. Journal of Architecture and Civil Engineering, 2005, 22(1): 71-75. |
| [7] | 张建仁,张克波,彭辉,等. 锈蚀钢筋混凝土矩形梁正截面抗弯承载力计算方法[J]. 中国公路学报,2009, 22(3): 45-51. ZHANG Jian-ren, ZHANG Ke-bo, PENG Hui, et al. Calculation Method of Normal Section Flexural Capacity of Corroded Reinforced Concrete Rectangular Beams[J]. China Journal of Highway and Transport, 2009, 22(3): 45-51. |
| [8] | MALUMBELA G, MOYO P, ALEXANDER M. Behaviour of RC Beams Corroded under Sustained Service Loads[J]. |
| [9] | MALUMBELA G, ALEXANDER M, MOYO P. Variation of Steel Loss and Its Effect on the Ultimate Flexural Capacity of RC Beams Corroded and Repaired under Load[J]. |
| [10] | DU Y, CULLEN M, LI C. Structural Performance of RC Beams under Simultaneous Loading and Reinforcement Corrosion[J]. |
| [11] | MALUMBELA G, ALEXANDER M, MOYO P. Lateral Deformation of RC Beams under Simultaneous Load and Steel Corrosion[J]. |
| [12] | 李剑,孙建渊.超载对大型公路桥梁结构的损伤评估及诊断方法研究[J].重庆交通学院学报,2006,25(6):19-21,58. LI Jian, SUN Jian-yuan. Damage Evaluate and the Method of Diagnose Study of Great Highway Bridge Structure by Over Loading[J]. Journal of Chongqing Jiaotong University,2006, 25(6): 19-21,58. |
| [13] | 孙晓燕,王海龙,黄承逵.超载运营对服役桥梁受弯性能影响的试验研究[J].浙江大学学报:工学版, 2008,42(1):152-156. SUN Xiao-yan, WANG Hai-long, HUANG Cheng-kui. Experimental Investigation on Flexural Performance of Bridge Members under Overloading[J].Journal of Zhejiang University:Engineering Science Edition,2008, 42(1):152-156. |
| [14] | 孙晓燕,黄承逵,赵国藩,等.超载对桥梁构件受弯性能影响的试验研究[J].土木工程学报,2005, 38(6):35-40. SUN Xiao-yan, HUANG Cheng-kui,ZHAO Guo-fan,et al. Experimental Study of the Influence Truck Overloads on the Flexural Performance of Bridge Members[J].China Civil Engineering Joural. 2005, 38(6):35-40. |
| [15] | 刘扬,江楠,邓扬. 持续荷载与氯离子共同作用下RC梁抗弯试验研究[J].公路交通科技, 2014,31(10):65-70. LIU Yang, JIANG Nan, DENG Yang. Experimental Study on Flexure Behavior of RC Beams under Combined Action of Sustained Loading and Chloride Ions[J]. Journal of Highway and Transportation Research and Development, 2014, 31(10):65-70. |
| [16] | CAPOZUCCA R, CERRI M N. Identification of Damage in Reinforced Concrete Beams Subjected to Corrosion[J]. ACI Structural Journal, 2000, 97(6):902-909. |
| [17] | 徐善华. 混凝土结构退化模型与耐久性评估[D]. 西安:西安建筑科技大学,2003. XU Shan-hua. Models of Deterioration of Reinforced Concrete Structure and Durability Evaluation[D]. Xi'an: Xi'an University of Architecture and Technology, 2003. |
| [18] | MALUMBELA G, MOYO P, ALEXANDER M. Longitudinal Strains and Stiffness of RC Beams under Load as Measures of Corrosion Levels[J]. Engineering Structures, 2012, 35(1): 215-227. |
| [19] | 张永利. 锈蚀钢筋混凝土构件粘结性能及承载性能研究[D]. 西安:西安建筑科技大学,2011. ZHANG Yong-li. Bonding Properties and Bearing Capacity of Corroded Reinforced Concrete Member[D]. Xi'an: Xi'an University of Architecture and Technology, 2011. |
| [20] | 任宝双,钱稼茹,聂建国. 在用钢筋混凝土简支桥面梁受弯刚度估算[J]. 工业建筑,2001, 31(1): 13-15. REN Bao-shuang, QIAN Jia-ru, NIE Jian-guo. Evaluation of Bending Stiffness for Existing Simply Supported RC Bridge Beams[J]. Industrial Construction 2001,31(1):13-15. |
| [21] | 过镇海,时旭东. 钢筋混凝土原理和分析[M]. 北京:清华大学出版社,2003. GUO Zhen-hai, SHI Xu-dong. Reinforced Concrete Theory and Analysis[M]. Beijing: Tsinghua University Press, 2003. |
| [22] | GB 50010—2010, 混凝土结构设计规范[S]. GB 50010—2010, Code for Design of Concrete Structures[S]. |
| [23] | 邢国华,牛荻涛. 锈蚀钢筋混凝土梁的受弯分析模型[J]. 中南大学学报:自然科学版, 2014,45(1):193-201. XING Guo-hua, NIU Di-tao. Analytical Model of Flexural Behavior of Corrode Reinforced Concrete Beams[J]. Journal of Central South University:Science and Technology Edition, 2014,45(1):193-201. |
 2016, Vol. 31
2016, Vol. 31
