扩展功能
文章信息
- 张玉平, 谢文昌, 李传习
- ZHANG Yu-ping, XIE Wen-chang, LI Chuan-xi
- 无铺装层PK断面混凝土梁日照温度场分析
- Analysis of Temperature Field of PK Section Concrete Girder without Pavement Caused by Solar Radiation
- 公路交通科技, 2016, Vol. 31 (4): 59-65
- Journal of Highway and Transportation Research and Denelopment, 2016, Vol. 31 (4): 59-65
- 10.3969/j.issn.1002-0268.2016.04.010
-
文章历史
- 收稿日期: 2015-05-04
太阳辐射将使混凝土主梁截面产生非线性梯度温度。当这种梯度温度引起的变形被结构内、外约束阻碍时,会产生相当大的温差应力[1]。近年来,极端高温天气频繁出现,太阳辐射对桥梁结构的影响越来越受重视,这种影响定量分析的关键首先是合理确定其温度场。我国《公路桥涵设计通用规范(JTG D60—2004)》(简称《公路桥规》)[2]给出了桥梁结构梯度温度荷载的相应取值,但仅限于有铺装层的混凝土梁和带混凝土桥面板的钢结构,且是将这一荷载作为可变作用施加于成桥之后的结构。对于施工过程中无铺装层混凝土梁存在的梯度温度在设计计算中是否考虑、如何取值,并未规定。研究表明,桥面铺装对混凝土梁竖向日照温差有明显的削弱作用[3, 4],施工过程中无铺装层混凝土梁的温度效应不容忽视。
近50年来,国内外学者基于热传导理论和实测数据,运用有限元方法对混凝土梁日照温度场进行了大量研究[5, 6, 7, 8, 9, 10, 11]。Soukhov[12]、肖建庄[13]和顾斌[14]先后通过对气象参数的概率分析,拟合得到桥址地区有铺装层混凝土梁出现的竖向梯度温度模式。文献[3]在对无铺装层混凝土梁实测数据的基础上提出了呈指数函数分布的梯度温度模式,但仅适用于桥梁所在地区。另外,国内外对混凝土梁温度场的研究主要是针对形状规则的箱形截面梁,对于平行设置的双幅箱梁桥,叶见曙[15]认为可按照单幅箱梁来考虑。文献[4]中发现双箱对腹板内侧温度没有大的影响,而对腹板外侧影响较大,这种差异主要与桥梁所在地理位置及桥梁走向有关。而PK断面(美国 Pasco-Kennewick 桥首次采用了双三角形边箱形式主梁,这种断面形式简称为 PK 断面)主梁的温度场与普通箱形截面梁分布是否相同,则值得研究。
本文以马鞍山长江公路大桥右汊斜拉桥为工程背景,借助有限元软件ANSYS对无铺装层PK断面混凝土梁的日照温度场进行计算,并与混凝土PK主梁的温度场实测数值进行了对比;对影响混凝土梁温度场分布的主要因素进行参数分析;采用指数函数的形式对其竖向梯度温度进行拟合,并与《公路桥规》、铁路桥规、英国规范等设计规范中有关混凝土梁梯度温度的规定进行比较研究。
1 热传导基本理论及方程处于自然环境中的混凝土梁日照温度场应按瞬态传热问题进行分析,在笛卡尔坐标系中,三维瞬态导热微分方程的一般形式为[16]
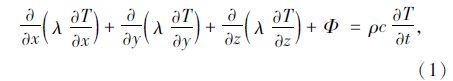
对于混凝土桥梁结构,沿桥纵向温度均匀分布,故可简化为常物性、无内热源的二维瞬态导热微分方程
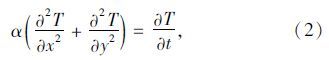
求解混凝土梁的温度分布,实质上是在定解条件下求解微分方程(2)。对于瞬态热传导问题,定解条件包括初始条件和边界条件,初始条件即计算初始时刻混凝土梁的温度分布,可表示为

边界条件则是反映影响物体热传导和温度状态的外部因素,在日照作用下,混凝土桥梁与外界的热交换,主要有来自太阳辐射的热流,以及与周围环境之间的对流及辐射换热,其边界条件是由第二类和第三类边界条件组成的混合边界条件,可以表示为:
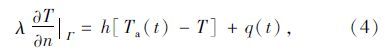
式(4)可以进一步改写成由太阳辐射热流密度qs、对流换热热流密度qc及辐射换热热流密度qr表示的传热边界条件:
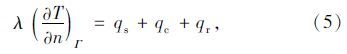

qc根据Newton冷却定律表示为:
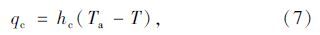
qr根据Stefen-Boltzmann定律表示为:
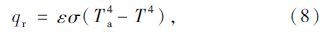
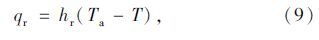
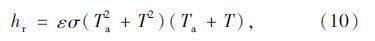
将式(6)、(7)和(9)代入式(5),可将混凝土箱梁的箱外边界条件最终处理为第三类边界:
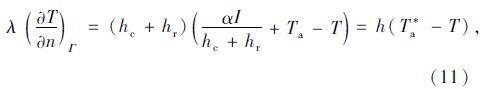
同理,箱内边界条件也可以处理为这种形式,由于箱内没有太阳辐射,相应的综合大气温度中不包含太阳辐射项。
在ANSYS中,将h,Ta*作为荷载施加在相应的边界上,即可求解。
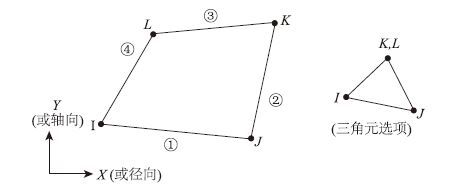
2 有限元模型的建立采用有限元软件ANSYS模拟无铺装层PK断面混凝土梁的日照温度场,选用具有二维热传导能力的平面单元PLANE55模拟平面温度场[17],PLANE55单元具有4个节点,每个节点只有一个自由度,单元示意图见图 1。
|
| 图 1 PLANE55单元示意图 Fig. 1 Schematic diagram of PLANE55 element |
按马鞍山长江公路大桥右汊斜拉桥标准断面的实际尺寸建立模型,对其进行网格划分,整个模型由5 142个节点、4 335个单元组成,如图 2所示。以6:00时刻的箱梁实测温度作为初始条件,将太阳辐射、对流及辐射换热按变换后的第三类边界条件施加。根据实测数据或参考相关文献,确定计算所需的混凝土材料物理参数值和边界参数值,见表 1~表 4[4, 16, 18, 19, 20]。利用Table数组定义荷载,计算时间为2013年9月1日6:00-9月2日6:00,全过程分为25个荷载步,每个荷载步分为3个子荷载步。部分计算结果见图 3。

|
| 图 2 主梁断面模型图 Fig. 2 Model of girder section |
| 参数 | 密度ρ/(kg·m-3) | 比热容c/ [J·(kg·K)-1] | 导热系数k/ [W·(m·K)-1] | 吸收率α | 辐射率ε |
| 数值 | 2 472 | 960 | 2.71 | 0.5 | 0.88 |
| 时刻 | 6:00 | 7:00 | 8:00 | 9:00 | 10:00 | 11:00 | 12:00 | 13:00 | 14:00 | 15:00 | 16:00 | 17:00 | 18:00 |
| 顶板 | 26.4 | 194.2 | 420.7 | 631.8 | 798.4 | 904.4 | 940.8 | 904.4 | 798.4 | 631.8 | 420.7 | 194.2 | 26.4 |
| 底板 | 5.3 | 38.8 | 84.1 | 126.4 | 159.7 | 180.9 | 188.2 | 180.9 | 159.7 | 126.4 | 84.1 | 38.8 | 5.3 |
| 南侧边腹板 | 13.9 | 62.6 | 182.7 | 312.7 | 420.9 | 491.2 | 515.5 | 491.2 | 420.9 | 312.7 | 182.7 | 62.6 | 13.9 |
| 北侧边腹板及中腹板 | 15.4 | 53.6 | 81.6 | 103.8 | 120.4 | 130.6 | 134.1 | 130.6 | 120.4 | 103.8 | 81.6 | 53.6 | 15.4 |
| 注:本文中太阳辐射强度是参照文献[16],根据桥梁所在地理位置和混凝土梁各表面朝向确定太阳常数、太阳时角和太阳入射角等参数,通过计算得到。 | |||||||||||||
| 时刻 | 5:00 | 7:00 | 9:00 | 11:00 | 13:00 | 14:00 | 15:00 | 17:00 | 19:00 | 21:00 | 23:00 | 1:00 | 3:00 | 5:00 |
| 箱外 | 22.0 | 23.0 | 26.0 | 28.8 | 27.5 | 29.0 | 29.5 | 27.5 | 25.5 | 25.0 | 24.0 | 23.0 | 23.4 | 22.0 |
| 南侧箱内 | 28.0 | 27.8 | 27.8 | 28.3 | 28.8 | 29.0 | 29.2 | 29.5 | 29.5 | 29.5 | 29.2 | 28.8 | 28.4 | 28.3 |
| 北侧箱内 | 27.0 | 26.7 | 27.2 | 27.5 | 27.8 | 28.0 | 28.3 | 28.0 | 28.0 | 28.0 | 28.0 | 27.8 | 27.3 | 27.0 |
| 注:箱梁内外温度是通过在相应位置设置测点,实测得到。 | ||||||||||||||

|
| 图 3 实测温度和计算温度变化图 Fig. 3 Variations of measured and calculated temperatures |
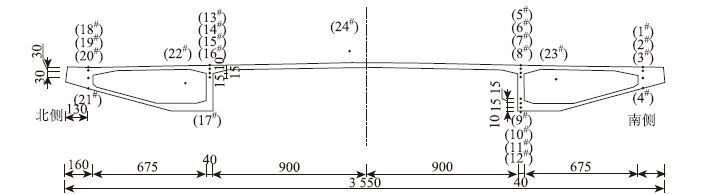
在马鞍山长江公路大桥右汊斜拉桥的施工过程中,选择马鞍山侧主梁(桥面尚未铺装)20#梁段中间断面进行温度场观测,测点布置如图 4所示,全断面共布置了24个测点。测试元件为热电偶传感器。选择无云、微风条件下日照辐射较为直接的天气进行温度场周期性观测,选取一组实测数据(2013年9月1日6:00—9月2日6:00)和对应ANSYS 分析结果进行比较分析。
|
| 图 4 截面尺寸与测点布置图(单位:cm) Fig. 4 Section dimensions and measuring point positions(unit:cm) |
图 3表明,计算值与实测值吻合较好,ANSYS模型较好地模拟了混凝土梁的日照温度场及内部各点温度变化趋势。从图中可以看出,腹板温度与底板温度变化趋势相类似,腹板温度较底板要高,且腹、底板温度峰值时刻较顶板均延迟3 h左右。
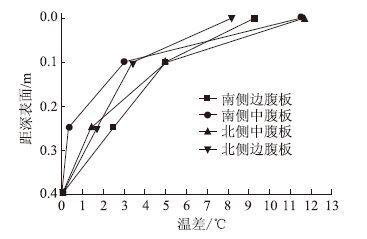
根据《公路桥规》竖向梯度温度取值的规定,本文取PK断面混凝土梁各个腹板距顶面0.4 m范围内竖向温度梯度分布,见图 5。图 5所示的箱梁南侧边腹板、南侧中腹板、北侧中腹板和北侧边腹板的最大竖向温差分别为8.2,11.7,11.5 ℃和9.3 ℃,可见各腹板的最大竖向温差并不一致,中腹板最大竖向温差明显高于边腹板。
|
| 图 5 竖向梯度温度分布图 Fig. 5 Distributions of vertical gradient temperatures |
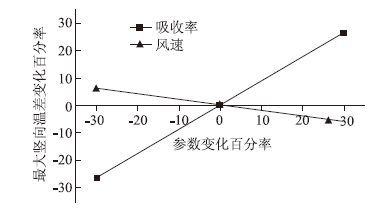
无铺装层PK断面混凝土梁日照温度场的计算模型已得到实测结果的验证,可以用于无铺装层混凝土梁日照温度场的影响因素的参数分析。在无铺装层混凝土梁日照温度场的影响因素中,混凝土密度、比热容可以通过实测得到,导热系数可以通过实测数据反算[4],混凝土辐射率在各文献中的取值介于0.85~0.95之间,离散性均不大;太阳辐射强度可以通过桥址位置和表面朝向等参数计算得到;箱梁内外大气温度可以通过实测得到。受到表面粗糙度、颜色等因素影响,混凝土表面太阳辐射吸收率在各文献中的取值波动较大;影响混凝土表面对流换热系数的主要因素——风速存在一定的随机性。因此,下面研究吸收率和风速对无铺装层混凝土梁日照温度场的影响。应用控制变量法,按照本文取值±30% 的增幅改变二者的取值,对吸收率和风速进行参数分析。计算结果如图 6所示。
|
| 图 6 参数影响分析曲线(单位:%) Fig. 6 Analysis curves of parameter impact(unit:%) |
图 6表明,无铺装层混凝土梁最大竖向温差变化与吸收率变化、风速变化基本呈线性关系,吸收率的影响较大,风速次之。吸收率决定混凝土对太阳辐射的吸收量,吸收率变化±30%会导致最大竖向温差变化±26%左右。风速则是影响无铺装层混凝土箱梁温度场的另一个重要参数,风速的大小影响着箱梁表面与大气对流换热的效率。
5 竖向梯度温度的计算研究温度场的主要目的是确定结构的竖向梯度温度,以便计算结构由于梯度温度产生的应力。对于无铺装层PK断面混凝土梁,可利用已得到验证的模型计算其在极端天气条件下的温度场,从而确定施工过程中存在的最不利梯度温度。根据桥址所在地区的气象数据,2013年当地极端天气出现在8月12日,最高气温和最低气温分别为41 ℃和30 ℃,微风。应用本文第2节中的方法计算太阳辐射强度、综合换热系数。由于每天的大气温度大致按正弦曲线规律变化,可根据最高气温和最低气温按下式计算各个时刻的大气温度[16]:
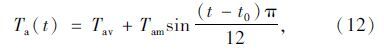
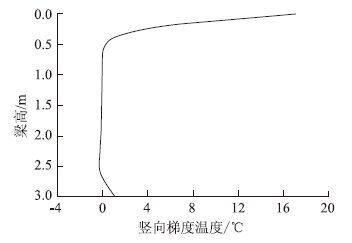
箱内温度变化较为平缓,可按实测数据中大气温度与箱内温度的差值关系进行换算;对于初始条件的确定,可先假设一初始温度,通过计算2个周期(48 h)得到趋于稳定的箱梁温度,以此时的箱梁温度作为初始条件,进行箱梁温度场计算。计算得到的箱梁中腹板竖向梯度温度可用指数函数17.1e-8.3y表示,从图 7中可知,底板温度与腹板相差很小。对于PK断面,计算与实测结果均表明截面下缘基本无竖向温差,建议不考虑截面下缘梯度温度。
|
| 图 7 竖向梯度温度拟合曲线 Fig. 7 Fitted curve of vertical gradient temperature |
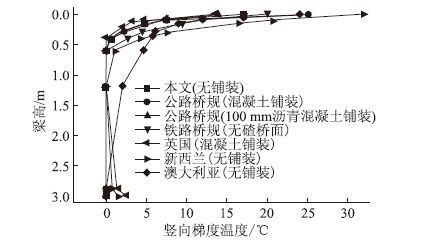
计算得到的竖向梯度温度模式与各国规范规定的梯度温度模式对比见表 5及图 8。对比结果表明,本文研究得到的无铺装层PK断面混凝土梁的梯度温度分布趋势与各国规范相关规定的趋势基本吻合,但具体数值有一定差别,本文取值与新西兰规范相差最大,温度最大值相差14.9 ℃。由于温度分布受地域影响,选取准确的温度荷载是保证结构温度计算准确的前提,且对结构而言无铺装层温度梯度应比有铺装层的温度梯度更加不利,因此有必要补充完善《公路桥规》中关于无铺装层混凝土梁梯度温度的规定。
| 梁高/m | 温度/℃ | |||
| 本文(无铺装) | 铁路桥规 (无碴桥面) | 新西兰(无铺装) | 澳大利亚(无铺装) | |
| 0.0 | 17.1 | 20 | 32 | 24 |
| 0.1 | 7.5 | 12.1 | 20.7 | 12 |
| 0.15 | 4.9 | 9.4 | 16.4 | 9 |
| 0.3 | 1.4 | 4.5 | 7.6 | 6 |
| 0.4 | 0.6 | 2.7 | 4.2 | 5.6 |
| 0.6 | 0.0 | 0.0 | 1.0 | 4.7 |
| 1.2 | 0.0 | 0.0 | 0.0 | 2.0 |
| 2.9 | 0.0 | 0.0 | 0.75 | 0.0 |
| 3.0 | 0.0 | 0.0 | 1.5 | 0.0 |
|
| 图 8 梯度温度模式对比图 Fig. 8 Contrast of curves of gradient temperature modes |
(1)通过建立ANSYS模型,计算了无铺装层PK断面混凝土梁日照温度场,同时采集了实桥温度场数据,计算值与实测值吻合较好。结果表明各腹板的最大竖向温差不一致,中腹板的最大竖向温差明显高于边腹板。
(2)参数分析结果表明,无铺装层混凝土梁最大竖向温差变化与吸收率变化、风速变化基本呈线性关系。吸收率对混凝土梁最大竖向温差影响较大,风速也会产生一定的影响。
(3)计算得到无铺装层混凝土梁竖向梯度温度的指数函数形式,其分布趋势与各国规范的无铺装层温度梯度分布趋势基本一致,但其数值与各国规范相关规定值相比存在一定的差别,建议补充完善《公路桥规》中关于无铺装层混凝土梁梯度温度的规定。
| [1] | 刘兴法.混凝土结构的温度应力分析[M].北京:人民交通出版社,1991:1-4. LIU Xing-fa. Analysis of Thermal Stress for Concrete Structure[M]. Beijing: China Communications Press, 1991: 1-4. |
| [2] | JTG D60—2004,公路桥涵设计通用规范[S]. JTG D60—2004,General Code for Design of Highway Bridges and Culverts[S]. |
| [3] | 方志,汪剑.大跨预应力混凝土连续箱梁桥日照温差效应[J].中国公路学报,2007,20(1):62-67. FANG Zhi, WANG Jian. Sun Light Thermal Difference Effect on Long-span PC Continuous Box Girder Bridge[J]. China Journal of Highway and Transport, 2007, 20(1): 62-67. |
| [4] | 聂玉东.寒区大跨径混凝土箱梁桥温度场及温度效应分析[D].哈尔滨:哈尔滨工业大学,2013. NIE Yu-dong. Analysis of Temperature Field and Temperature Effect for Long Span Concrete Box Girder Bridges in Cold Regions[D]. Harbin: Harbin Institute of Technology, 2013. |
| [5] | 汪剑,方志.混凝土箱梁桥的温度场分析[J].湖南大学学报:自然科学版,2008,35(4):23-28. WANG Jian, FANG Zhi. Temperature Variation of Concrete Box Girder Bridge[J]. Journal of Hunan University:Natural Science Edition, 2008, 35(4): 23-28. |
| [6] | 吴六政.混凝土箱梁桥温度场的模拟[J].公路交通科技,2011, 28(10):65-69. WU Liu-zheng. Simulation of Temperature Field of Concrete Box-girder Bridge[J]. Journal of Highway and Transportation Research and Development,2011, 28(10): 65-69. |
| [7] | ROBERTS-WOLLMAN C L, BREEN J E, CAWRSE J. Measurements of Thermal Gradients and Their Effects on Segmental Concrete Bridge[J]. Journal of Bridge Engineering, 2002, 8(3): 166-174. |
| [8] | MONDAL P, DEWOLF J T. Development of Computer-Based System for the Temperature Monitoring of a Post Tensioned Segmental Concrete Box Girder Bridge[J]. |
| [9] | YAN P. Research on Temperature Field and Temperature Stress of Large Span Concrete Cable-Stayed Bridge Girder[C]//Applied Mechanics and Materials. Yantai:[s.n.], 2012:2073-2080. |
| [10] | LEE J H, KALKAN L. Analysis of thermal Environmental Effects on Precast, Prestressed Concrete Bridge Girders: Temperature Differentials and thermal Deformations[J]. |
| [11] | LARSSON O, THELANDERSSON S. Estimating Extreme Values of Thermal Gradients in Concrete Structures[J]. |
| [12] | SOUKHOV D. Representative Values of Thermal Actions for Concrete Bridge[J]. |
| [13] | 肖建庄,宋志文,赵勇,等.基于气象参数的混凝土结构日照温度作用分析[J]. 土木工程学报,2010,43(4):30-36. XIAO Jian-zhuang, SONG Zhi-wen, ZHAO Yong, et al. Analysis of Solar Temperature Action for Concrete Structure Based on Meteorological Parameters[J]. China Civil Engineering Journal, 2010, 43(4): 30-36. |
| [14] | 顾斌,陈志坚,陈欣迪.基于气象参数的混凝土箱梁日照温度场仿真分析[J].东南大学学报:自然科学版,2012,42(5):950-955. GU Bin, CHEN Zhi-jian, CHEN Xin-di. Simulation Analysis for Solar Temperature Field of Concrete Box Girder Based on Meteorological Parameters[J]. Journal of Southeast University: Natural Science Edition,2012, 42(5): 950-955. |
| [15] | 叶见曙,贾琳,钱培舒.混凝土箱梁温度分布观测与研究[J].东南大学学报:自然科学版,2002,32(5):788-793. YE Jian-shu, JIA Lin, QIAN Pei-shu. Observation and Research on Temperature Distribution in Concrete Box Girders[J]. Journal of Southeast University: Natural Science Edition, 2002, 32(5): 788-793. |
| [16] | 彭友松.混凝土桥梁结构日照温度效应理论及应用研究[D].成都:西南交通大学,2007. PENG You-song. Study on Theory of Solar Radiation Thermal Effects on Concrete Bridges and Application[D]. Chengdu: Southwest Jiaotong University, 2007. |
| [17] | 美国ANSYS公司北京办事处.ANSYS热分析指南[M].北京:美国ANSYS公司北京办事处,2000. Beijing Office of US ANSYS Inc. ANSYS Thermal Analysis Guide[M]. Beijing: Beijing Office of US ANSYS Inc., 2000. |
| [18] | 张建荣,徐向东,刘文燕.混凝土表面太阳辐射吸收系数测试研究[J].建筑科学, 2006,22(1):42-45. ZHANG Jian-rong, XU Xiang-dong, LIU Wen-yan. A Test Study on the Solar Radiation Absorption Coefficient of Concrete Surface[J]. Building Science, 2006, 22(1): 42-45. |
| [19] | 刘照球.混凝土结构表面对流换热研究[D].上海:同济大学,2006. LIU Zhao-qiu. Research for Convection Heat Transfer of Surface of Concrete Structure[D]. Shanghai: Tongji University, 2006. |
| [20] | 张玉平,杨宁,李传习.无铺装层钢箱梁日照温度场分析[J].工程力学, 2011, 28(6):156-162. ZHANG Yu-ping, YANG Ning, LI Chuan-xi. Research of Temperature Field of Steel Box Girder without Pavement Caused by the Solar Radiations[J]. Engineering Mechanics, 2011, 28(6):156-162. |
 2016, Vol. 31
2016, Vol. 31
