扩展功能
文章信息
- 王昌衡, 柏理想, 邓珊
- WANG Chang-heng, BAI Li-xiang, DENG Shan
- 基于熵权组合预测与粗糙模糊集的沥青路面使用性能分析
- Analysis of Asphalt Pavement Performance Based on Entropy Weight Combination Forecast and Rough Fuzzy Set
- 公路交通科技, 2016, Vol. 31 (4): 12-19
- Journal of Highway and Transportation Research and Denelopment, 2016, Vol. 31 (4): 12-19
- 10.3969/j.issn.1002-0268.2016.04.003
-
文章历史
- 收稿日期: 2014-11-12
路面使用性能的评价与预测能够帮助道路管理者判定路面使用性能的好坏并分析路面使用性能变化趋势,是合理制订养护维护计划、进行投资决策的重要依据之一。以往在对沥青路面使用性能进行预测时,多采用单一预测方法进行预测,或者对多预测方法精度比较优选后进行预测[1]。采用单一预测方法时,预测方法的合理性与结果的最优性均无法保证;而采用多预测方法精度比较优选后预测,舍弃了预测精度较次的其他方法的预测结果,但实际上预测对象往往有多种因素对其产生错综复杂的影响,而且不同的预测方法各有其优缺点。每种预测方法对己有数据的处理原则也不尽相同,因此多方法精度优选后预测有可能造成部分有用信息的丢失,降低预测的精确性与可靠性。而以往在对沥青路面使用性能进行评价时,大多是对沥青路面使用性能的优劣进行定性总结,而对沥青路面使用性能与其影响因素之间的关系很少涉及。实际上沥青路面使用性能的定性评价只是结果,找出影响沥青路面使用性能的主要因素,并有针对性地加以改进,才能更加有针对性、更加有效地提高沥青路面使用性能。
组合预测方法是按照一定的规则把不同预测模型的预测值组合起来,综合而全面地利用各个单项预测方法所提供的信息,并以适当的加权平均形式计算得出组合预测模型[2]。在预测实践中,若能把多种单项预测方法通过一定的规则组合起来,就可以让组合预测结果降低对某个精度较差的预测方法的敏感度,所以该方法一般能够提高预测的精确度与可靠度。而且该方法综合考虑了各个预测方法的信息,因此最大程度地避免了信息的丢失,得到的路面使用性能预测结果也更加全面稳妥。组合预测模型预测精度的高低在于能否科学合理地确定各个单项模型的加权平均系数,熵权组合预测法就是组合预测方法中权计算理论成熟、使用较为广泛的预测方法之一[3, 4, 5, 6, 7]。对于路面使用性能及其影响因素之间关系的研究,灰色关联分析法、主成分分析法只能对各影响因素的重要性进行分析,而无法揭示各影响因素与路面使用性能之间的制约关系[8]。而变精度粗糙模糊集不仅可以分析影响因素的重要性,明确影响因素与路面使用性能之间的制约关系,而且相对于一般的粗糙集理论[9, 10, 11, 12, 13],其输出的概率模糊性,更加切合自然推理过程,分析过程更加科学,结果也更加贴近实际。
1 系统建模 1.1 影响因素甄选沥青路面使用性能的影响因素众多,根据相关文献的研究成果[14],影响较大的因素主要可归纳为6类:
(1)交通条件
交通量既是沥青路面的主要使用功能,也是影响沥青路面使用功能的重要外部因素。在其他条件一样的情况下,交通量越大,路面使用性能将越低。
(2)气象条件
不良气象条件较易造成路面沉降、开裂,降低路面使用性能。同时,气象条件也会对诸如路面排水、施工、养护造成影响,间接影响沥青路面使用性能。
(3)水土条件
沥青路面在道路周边水土条件不佳的情况下(如排水不畅,道路土质不佳),很容易造成路面水浸或塌陷,影响路面的使用性能与使用寿命。
(4)材料因素
沥青路面材料多种多样,优良的路面材料将大大提高路面使用性能与耐久性。
(5)施工水平
道路的施工水平对沥青路面使用性能有重要影响,施工队伍的组织结构与操作水平、施工工艺以及施工的机械化程度都会对道路建设质量造成重要影响,进而影响沥青路面使用性能。
(6)养护水平
在道路建成后,较高的养护水平将大大提高沥青路面使用性能与路面使用寿命。
1.2 熵权组合预测根据沥青路面使用性能变化规律,在沥青路面建成后,如无任何养护措施,其使用性能是随着时间而日益下降的,而且下降速度是逐渐变大的。在进行外部养护后,沥青路面使用性能下降过程会因外部养护情况而趋于缓和。沥青路面使用性能下降的过程是随时间这种单一变量而不断变化的,可用单变量模型来进行模拟。在利用单变量模型进行模拟的基础上,再对路面使用性能的预测结果加以组合预测。
组合预测方法按加权系数计算方式的不同分为最优组合预测和非最优组合预测。熵权法通过全面研究各个预测方法的误差指标值,以误差指标值的大小确定各个预测方法在组合预测模型中的权重。它是一种客观赋权方法,也是一种比较常用的非最优正权组合预测模型。
若有m种预测方法进行路面使用性能预测,则熵权法组合预测的基本过程如下:
步骤1:对于某个序列指标{at},有m种预测模型对其进行预测,设第i种预测模型在t时刻的预测值为ait,则第i种预测模型在t时刻的预测相对误差eit为:
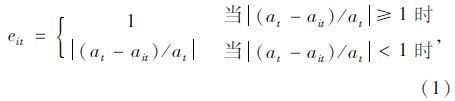
步骤2:将各种单项预测方法预测相对误差序列进行归一化,即计算第i种单项预测方法第t时刻的预测相对误差eit的比例pit:

步骤3:计算第i种单项预测方法的预测相对误差的熵值hi。
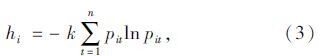
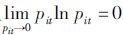 。
。
步骤4:计算第i种单项预测方法的变异程度系数di。
根据系统中某项指标的熵权值的大小与其变异程度相反的原则,得出定义第i种单项预测方法所对应的预测相对误差序列的变异程度系数di为:

步骤5:计算第i种单项预测方法的加权系数wi。
某个单项预测方法的变异程度越大,则它在组合预测中相应的权系数就应越小,据此得到第i种预测单项预测方法的权系数wi:
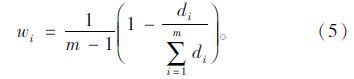
步骤6:计算得到t时刻的组合预测最终值t:

组合预测方法可对任意的单一预测方法进行组合,而神经网络预测法与灰色预测法均为比较常用的单一预测方法。而按照网络的拓扑结构及学习方法,神经网络[15, 16]可以分为多种形式,其中BP神经网络是目前应用最为广泛,理论最为成熟的神经网络模型之一。而灰色预测通常包括模型识别、参数估算和预测3个环节,由于路面使用性能是随时间变量而变化的,因此对其预测比较适用的灰色预测模型[17, 18]为单变量预测模型的GM(1,1)模型、verhulst模型等。
1.3 粗糙模糊集分析粗糙模糊集[19, 20]是粗糙集与模糊集的一种杂合理论。本质上,粗糙集与模糊集都研究信息粒度的问题,粗糙集研究粗糙非交迭类别及粗糙概念,而模糊集研究交迭集合间的模糊性。当知识库中的知识模块都是清晰概念,而近似的概念或输出类别具有病态边界,输入模式集合的不可分辨关系与输出类别的模糊性同时出现,这样就需要粗糙模糊集进行研究。而变精度粗糙模糊集[21]是粗糙模糊集的一种推广与发展,在变精度粗糙模糊集中,近似空间是清晰的,决策属性是模糊的。变精度粗糙模糊集算法设计过程如下:
步骤1:构建城市道路面使用性能的知识表示系统S=(U,A,V,f), 其中U为论域对象空间,即作为分析对象的各条城市道路或路段;A为属性的集合,包括条件属性集合C与决策属性集合D,即A=C∪D,且C∩D=Φ,其中条件属性集合C为交通条件、气象条件等城市道路路面使用性能的影响因素,决策属性集合D为城市道路路面使用性能的模糊划分;V为各类属性值域的并集,即V=∪Va,其中a∈A,Va为属性a的值域;f为信息函数,它指明了U×A→V的规则,对于∀a∈A,∀x∈U,f(x,a)∈Va。
步骤2:对于论域对象空间U,由交通条件、气象条件等条件属性集合C生成不可分辨关系I(x)。对于对象y,z,I(y,z)的定义为:I(x,y)={(y,z)∈U×U: f(y,a)=f(z,a),∀q∈C}。
步骤3:由决策属性集合D,生成决策类集合FX。决策类FX的定义为:
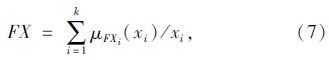
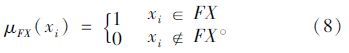
步骤4:对于∀λ∈[0, 1],计算决策类集合FX的λ-截集,形成模糊等价类FXλ,模糊等价类FXλ的定义为:
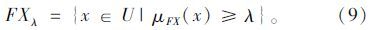
步骤5:计算决策类集合FX的λ-截集FXλ的隶属函数μFXλ为:
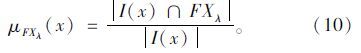
步骤6:根据设定的置信阈值β(理论上β的取值范围为[0,1],实际中β的取值范围一般为(0.5,1]),计算对于所有条件属性集C的分类质量γCβ(D)为:
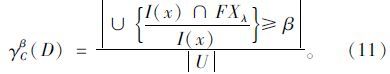
步骤7:在不影响分类质量的情况下,通过缩减条件属性集C,搜寻得到β-约简。
令R=C,S=R,对C中的第j个条件属性cj,计算条件属性集R-{cj}分类质量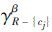 (D)。如果
(D)。如果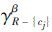 (D)=γSβ(D),则令S= R-{cj},R1=R,R=S。重复以上过程,直至γRβ(D)<γCβ(D)或R=R1。
(D)=γSβ(D),则令S= R-{cj},R1=R,R=S。重复以上过程,直至γRβ(D)<γCβ(D)或R=R1。
步骤8:以搜寻得到的β-约简,生成最少概率决策规则集。
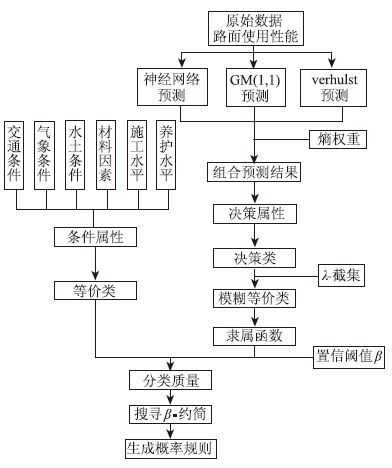
熵权组合预测与变精度粗糙模糊集的沥青路面使用性能系统分析建模流程见图 1。
|
| 图 1 系统建模流程图 Fig. 1 Flowchart of system modeling |
我国西南某市沥青路面设计使用年限一般为20 a,但近些年来,随着该市车流量的不断变大,以及原有部分路段存在施工不当、养护不合理等问题,导致该市部分路段路面损坏严重,路面使用性能下降速度大大超过预期。为对该市路面情况进行准确判断及预估,以便采取针对性措施提高路面使用性能,延长路段使用寿命,经相关部门统计,收集得到该市一批路段近8 a来基础统计数据(包括路段的国际平整度IRI,路面综合破损率DR,路面强度Ls,路面抗滑性能SFC以及路面湿度、温度Tw、w)。根据《公路沥青路面养护技术规范》(JTJ073.2—2001)中的相关计算方法,相应得到国际平整度指数RQI,路面状况指数PCI,路面结构强度系数SSI,路面抗滑性能SFC以及路面环境性能指数PEI,最终根据《高速公路养护质量检评办法》中推荐的公式计算得到反映道路路面使用性能的路面使用性能指数PQI见表 1。
| 路段编号 | 年份 | ||||||||
| 2006年 | 2007年 | 2008年 | 2009年 | 2010年 | 2011年 | 2012年 | 2013年 | 设计寿终年份 | |
| 1# | 90.13 | 89.27 | 88.34 | 87.14 | 86.34 | 85.19 | 83.92 | 82.10 | 2016 |
| 2# | 88.62 | 88.13 | 87.09 | 85.27 | 85.03 | 84.18 | 83.27 | 82.99 | 2019 |
| 3# | 89.41 | 88.09 | 87.21 | 86.32 | 85.17 | 84.08 | 82.53 | 81.48 | 2019 |
| 4# | 91.52 | 90.88 | 89.91 | 89.25 | 89.13 | 88.72 | 88.35 | 87.90 | 2017 |
| 5# | 90.43 | 88.71 | 87.04 | 85.99 | 84.75 | 83.19 | 82.31 | 81.13 | 2017 |
| 6# | 89.62 | 87.87 | 85.04 | 83.55 | 81.08 | 79.12 | 77.27 | 74.89 | 2018 |
| 7# | 88.29 | 86.38 | 85.04 | 83.39 | 81.07 | 79.11 | 77.77 | 75.10 | 2019 |
| 8# | 91.38 | 91.19 | 90.75 | 90.31 | 89.98 | 89.37 | 88.96 | 88.82 | 2016 |
| 9# | 91.07 | 90.82 | 90.44 | 90.63 | 89.71 | 89.10 | 88.59 | 88.38 | 2016 |
| 10# | 89.73 | 87.60 | 85.94 | 82.26 | 80.51 | 77.43 | 74.76 | 71.35 | 2015 |
| 11# | 89.66 | 89.27 | 88.81 | 88.55 | 87.88 | 87.37 | 86.80 | 86.67 | 2016 |
| 12# | 89.32 | 88.48 | 87.72 | 87.25 | 86.49 | 85.74 | 85.06 | 84.22 | 2015 |
| 13# | 91.76 | 88.02 | 86.36 | 84.62 | 82.18 | 80.29 | 77.51 | 75.05 | 2019 |
| 14# | 88.73 | 86.83 | 83.14 | 81.37 | 79.29 | 76.37 | 73.42 | 71.75 | 2016 |
利用多种预测模型分别对各路段的路面使用性能指数进行预测,得到设计使用年份的路面使用性能预测数据。以1#路段为例说明熵权组合预测模型的计算过程。
BP神经网络、GM(1,1)模型以及verhulst模型对1#路段的预测结果见表 2。
由表 2可知,BP模型、GM(1,1)模型以及verhulst模型的预测值与各路段路面使用性能指数的发展趋势一致,而且彼此之间预测精度相差也不大,这也说明BP模型、GM(1,1)模型以及verhulst模型对路面使用性能指数的预测均有其科学性与合理性,利用组合预测模型则能够综合这3类模型的信息特点,因此得到的预测结果也更加全面合理。以表 2中的数据为基础,根据模型中的式(1)~(5)所示的熵权计算过程,得到BP模型、GM(1,1)模型以及verhulst模型的熵权值分别为0.468 5,0.238 5,0.293 0。根据式(6)进而得到1#路段2006—2013年路面使用性能的组合预测值依次为89.31,88.13,87.39,86.38,84.67,83.62,82.97,82.72。组合预测模型的预测精度98.89%,残差平方和9.99,后验比值为0.256 3,小误差概率为100%,不仅预测精度极高,而且后验比值及小误差概率结果也表明组合预测可以进行长期预测。根据组合预测,到设计使用年限时的路面使用性能指数的预测结果为80.82。
| 年份 | 原始数据 | BP神经网络 预测值 | GM(1,1) 模型预测值 | verhulst模型 预测值 |
| 2006年 | 90.13 | 88.39 | 90.13 | 90.13 |
| 2007年 | 89.27 | 86.64 | 89.53 | 89.37 |
| 2008年 | 88.34 | 86.22 | 88.34 | 88.50 |
| 2009年 | 87.14 | 85.28 | 87.17 | 87.51 |
| 2010年 | 86.34 | 82.91 | 86.01 | 86.40 |
| 2011年 | 85.19 | 82.03 | 84.87 | 85.15 |
| 2012年 | 83.92 | 82.10 | 83.74 | 83.74 |
| 2013年 | 82.10 | 83.11 | 82.63 | 82.17 |
| 精度比较结果 | 相对精度/% | 97.44 | 99.76 | 99.86 |
| 残差平方和 | 43.98 | 0.59 | 0.22 | |
| 后验比值 | 0.497 7 | 0.106 4 | 0.058 4 | |
| 小误差概率/% | 100 | 100 | 100 |
依此类推,得到其他路段到设计使用年限时的路面使用性能指数的组合预测结果,最终结果见表 3。
| 路段编号 | 到达设计年限时预测值 | 熵权值 | 组合预测值 | ||||
| BP神经网络 | GM(1,1)模型 | verhulst模型 | BP神经网络 | GM(1,1)模型 | verhulst模型 | ||
| 1# | 84.33 | 79.38 | 76.39 | 0.468 5 | 0.238 5 | 0.293 0 | 80.82 |
| 2# | 81.98 | 77.68 | 79.70 | 0.293 2 | 0.359 1 | 0.347 7 | 79.64 |
| 3# | 85.94 | 75.44 | 73.73 | 0.371 5 | 0.341 8 | 0.286 7 | 76.06 |
| 4# | 87.21 | 86.06 | 87.03 | 0.353 7 | 0.266 1 | 0.380 2 | 86.84 |
| 5# | 79.56 | 76.38 | 77.59 | 0.359 1 | 0.324 1 | 0.316 8 | 77.91 |
| 6# | 73.59 | 65.96 | 64.25 | 0.442 1 | 0.321 1 | 0.236 8 | 68.93 |
| 7# | 72.90 | 65.80 | 60.63 | 0.326 3 | 0.348 0 | 0.325 7 | 66.43 |
| 8# | 88.69 | 87.45 | 87.73 | 0.457 6 | 0.268 2 | 0.274 2 | 88.09 |
| 9# | 88.28 | 87.02 | 86.76 | 0.425 6 | 0.345 5 | 0.228 9 | 87.50 |
| 10# | 67.46 | 67.39 | 64.60 | 0.371 7 | 0.381 1 | 0.247 2 | 66.73 |
| 11# | 85.98 | 85.16 | 85.51 | 0.453 0 | 0.317 3 | 0.229 7 | 85.61 |
| 12# | 83.52 | 82.98 | 82.73 | 0.326 4 | 0.369 6 | 0.304 0 | 83.08 |
| 13# | 72.26 | 64.55 | 63.32 | 0.299 6 | 0.365 3 | 0.335 1 | 66.45 |
| 14# | 66.91 | 65.14 | 64.97 | 0.421 5 | 0.325 9 | 0.252 6 | 65.84 |
根据该市路政、交通及气象等相关部门等提供的资料构建出该市沥青路面使用性能评价知识系统。由于该市所有路段均在同一城市,因此气象条件基本一致,可忽略气象条件的差异影响。将其路面使用性能影响因素作为条件属性(由于各条件属性多为综合评价,因此采用德尔菲法对各路段各因素进行满分100分制评分,分值越高,反映路面使用性能越好),以各路段到达设计年限时路面使用性能指数的组合预测值作为决策属性,构建出该市路面使用性能信息系统见表 4。
| 路段编号 | 条件属性C | 决策属性D | |||||
| 交通条件c1 | 水土条件c2 | 材料因素c3 | 施工水平c4 | 养护水平c5 | 路面使用性能指数d | ||
| 1# | 82.49 | 80.02 | 83.29 | 80.54 | 81.14 | 80.82 | |
| 2# | 77.73 | 78.39 | 75.51 | 80.09 | 72.80 | 79.64 | |
| 3# | 73.95 | 68.47 | 73.64 | 72.09 | 75.17 | 76.06 | |
| 4# | 86.75 | 83.53 | 86.23 | 83.28 | 81.45 | 86.84 | |
| 5# | 78.92 | 80.14 | 79.36 | 79.12 | 74.73 | 77.91 | |
| 6# | 66.37 | 72.28 | 67.44 | 69.84 | 67.09 | 68.93 | |
| 7# | 66.37 | 70.09 | 67.44 | 69.84 | 67.09 | 66.43 | |
| 8# | 85.21 | 84.90 | 80.46 | 87.19 | 82.18 | 88.09 | |
| 9# | 88.47 | 82.73 | 81.99 | 82.52 | 83.41 | 87.50 | |
| 10# | 62.13 | 64.69 | 66.19 | 72.40 | 68.11 | 66.73 | |
| 11# | 86.63 | 83.17 | 84.38 | 77.69 | 84.22 | 85.61 | |
| 12# | 82.95 | 79.33 | 84.19 | 84.26 | 80.57 | 83.08 | |
| 13# | 68.17 | 62.25 | 65.83 | 71.22 | 66.59 | 66.45 | |
| 14# | 67.42 | 69.31 | 69.11 | 63.92 | 67.20 | 65.84 | |
对路面使用性能知识系统中的各属性进行离散,对于条件属性,参考各条件属性取值范围按照人工离散方法将分值为[85, 100]归类为“好”,将分值为[70,85)归类为“中”,将分值为[0,70)归类为“差”。对于决策属性,相关规范中已有推荐分类标准,但是考虑到决策属性中所包含信息按照隶属函数分类将相对更加科学,因此采用隶属函数对决策属性进行离散。参照现有的路面综合评价标准,决策属性的隶属函数设计如下:

离散后得到的模糊决策系统见表 5。
| U | 条件属性C | 决策属性D | 决策属性模糊决策隶属值 | ||||||
| c1 | c2 | c3 | c4 | c5 | d | 优 | 良 | 中 | |
| n1 | 中 | 中 | 中 | 中 | 中 | 良 | 0.221 3 | 0.778 7 | 0 |
| n2 | 中 | 中 | 中 | 中 | 中 | 良 | 0.142 7 | 0.857 3 | 0 |
| n3 | 中 | 差 | 中 | 中 | 中 | 良 | 0 | 0.904 0 | 0.096 0 |
| n4 | 好 | 中 | 好 | 中 | 中 | 优 | 0.622 7 | 0.377 3 | 0 |
| n5 | 中 | 中 | 中 | 中 | 中 | 良 | 0.027 3 | 0.972 7 | 0 |
| n6 | 差 | 中 | 差 | 差 | 差 | 中 | 0 | 0.428 7 | 0.571 3 |
| n7 | 差 | 中 | 差 | 差 | 差 | 中 | 0 | 0.262 0 | 0.738 0 |
| n8 | 好 | 中 | 中 | 好 | 中 | 优 | 0.706 0 | 0.294 0 | 0 |
| n9 | 好 | 中 | 中 | 中 | 中 | 优 | 0.666 7 | 0.333 3 | 0 |
| n10 | 差 | 差 | 差 | 中 | 差 | 中 | 0 | 0.282 0 | 0.718 0 |
| n11 | 好 | 中 | 中 | 中 | 中 | 优 | 0.540 7 | 0.459 3 | 0 |
| n12 | 中 | 中 | 中 | 中 | 中 | 良 | 0.372 0 | 0.628 0 | 0 |
| n13 | 差 | 差 | 差 | 中 | 差 | 中 | 0 | 0.263 3 | 0.736 7 |
| n14 | 差 | 差 | 差 | 差 | 差 | 中 | 0 | 0.222 7 | 0.777 3 |
根据条件属性C,对路段对象集U进行划分,得到等价类U/C={X1,X2,X3,X4,X5,X6,X7,X8},X1={n1,n2,n5,n12},X2={n3},X3={n4},X4={n6,n7},X5={n8},X6={n9,n11},X7={n10,n13},X8={n14}。
根据条件属性D,对路段对象集U进行划分,得到决策类U/D={FH,FM,FL},其中优类FH={n4,n8,n9,n11},良类FM={n1,n2,n3,n5,n12 },中类FL={n6,n7,n10,n13,n14}。
根据式(8)~(10)得到各等价类相对于决策类的粗糙隶属度为:
X1相对优类FH的隶属度为0,相对良类FM的隶属度为0.809 2,相对中类FL的隶属度为0;
X2相对优类FH的隶属度为0,相对良类FM的隶属度为0.904 0,相对中类FL的隶属度为0;
X3相对优类FH的隶属度为0.622 7,相对良类FM的隶属度为0,相对中类FL的隶属度为0;
X4相对优类FH的隶属度为0,相对良类FM的隶属度为0,相对中类FL的隶属度为0.604 7;
X5相对优类FH的隶属度为0.706 0,相对良类FM的隶属度为0,相对中类FL的隶属度为0;
X6相对优类FH的隶属度为0.603 7,相对良类FM的隶属度为0,相对中类FL的隶属度为0;
X7相对优类FH的隶属度为0,相对良类FM的隶属度为0,相对中类FL的隶属度为0.727 3;
X8相对优类FH的隶属度为0,相对良类FM的隶属度为0,相对中类FL的隶属度为0.777 3。
为取得可靠的、概率大的规则,取置信阈值β=0.7=70%,得到所有条件属性集C的分类质量为:
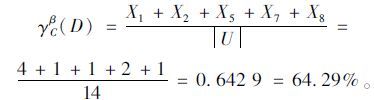
根据粗糙模糊集分析步骤7,在不影响分类质量的情况下,通过缩减条件属性集C,计算缩减属性后的条件属性集的分类质量与原条件属性集分分类质量等值原则搜寻β-约简,得到γC-{c1,c5}β(D)=γCβ(D),得到最小约简为C-{c1,c5},即约简为{c2,c3,c4}。 根据约简生成最少概率决策规则集见表 6。
| 规则 | 支持数 | 置信度/% |
| if水土条件=中,材料因素=中,施工水平=中,则路面使用性能=良 | 4 | 80.92 |
| if水土条件=差,材料因素=中,施工水平=中,则路面使用性能=良 | 1 | 90.40 |
| if水土条件=中,材料因素=中,施工水平=好,则路面使用性能=优 | 1 | 70.60 |
| if水土条件=差,材料因素=差,施工水平=中,则路面使用性能=中 | 2 | 72.73 |
| if水土条件=差,材料因素=差,施工水平=差,则路面使用性能=中 | 1 | 77.73 |
根据约简结果,可知在影响该市道路路面使用性能的所有因素中,决定路面使用性能的因素为水土条件、材料因素以及施工水平。而通过β-约简概率决策规则可知,“水土条件为中,材料因素为中以及施工水平为中,则路面使用性能为良”等5条规则的置信度均大于70%,可信度较高,可为该市沥青路面施工及养护提供参考。按照规则分析结果,该市路政部门对该市沥青路面水土条件差、路面材料差以及施工水平差的路段进行了改良,或采取措施改善了这些路段的排水系统或土质,或者置换了路面材料,甚至有些重新进行了施工。采取这些措施后,这些路段的路面使用性能有了显著提升,不仅路段同行能力有了显著提升,交通事故也有了明显减少。
3 结论(1)利用BP神经网络、GM(1,1)以及verhulst模型对沥青路面使用性能指数进行了预测,并计算出各模型的熵权;根据各模型预测结果及熵权对沥青路面使用性能指数进行了熵权组合预测;根据组合预测结果及相应规范,对沥青路面使用性能进行了基于模糊隶属函数分析的模糊决策评价。
(2)以路面使用性能模糊决策评价结果作为决策属性,以各影响因素作为条件属性,构建路面使用性能评价知识系统,对知识系统进行了基于置信度准则的变精度粗糙模糊集分析,得到了路面使用性能的决定性影响因素为水土条件、材料因素以及施工水平3个影响因素,并得到了5条置信度大于70%的较可靠规则,规则集分类质量为64.29%,分类质量较高。
(3)熵权组合预测模型综合考虑各模型的预测特征,虽然其预测精度可能不如最优预测模型,但却有效避免了次优模型信息的丢失,得到的预测结果更为全面合理。而变精度粗糙模糊集的路面使用性能分析,求解思路清晰,分析过程也更为严谨,且模型的置信度与分类质量可根据实际情况进行人为控制,应用更加灵活机动。经实践检验,该方法对路面使用性能的分析评价是有效的,可在路面使用性能的分析评价及相似领域中应用。
(4)本文的路面使用性能选取的影响因素为综合影响因素,采用评分制进行描述,实际上各影响因素可以进一步细分为定性或定量指标,但指标细化后,为了得到规则,需要海量的样本对象;同时,属性约简与规则生成的计算难度将呈几何级数般增加,在实际应用时,应根据样本对象个数,将影响因素细化到合适程度。
(5)实例中得到的规则支持数普遍较少,这是因为样本集对象较少的缘故。在实际应用中,为了提高规则的可靠性,大量的样本集对象是必要的。原则上,样本集对象越多,条件属性或最优约简所包含的属性数越少,规则支持数会越高,可靠性也会越高。且由于实例中选取的路段全部位于同一地区,因此忽略掉了气象条件的影响,当进行跨区域分析时,气象条件对路面使用性能的影响则不可忽略。
| [1] | 李志刚,邓学钧,顾锋.高速公路沥青路面使用性能评价模型的探讨[J].公路交通科技,2000,17(5):15-17.LI Zhi-gang,DENG Xue-jun, GU Feng. Evaluation Models for Serviceability of Freeway Asphalt Pavements[J]. Journal of Highway and Transportation Research and Development,2000,17(5):15-17. |
| [2] | 罗建科.神经网络与组合预测在高速公路路面管理系统的应用研究[D].成都:西南交通大学,2010.LUO Jian-ke. Research on Application of Neural Network and Combination Forecast in Expressway Pavement Management System[D].Chengdu: Southwest Jiaotong University,2010. |
| [3] | 张星,吴菊薪,陈惠,等.基于熵权的福建粮食产量组合预测模型[J].中国农业气象,2008,29(2):194-196.ZHANG Xing, WU Ju-xin, CHEN Hui, et al. A Combination Forecasting Model for Grain Crop Yield in Fujian Province Based on Entropy Weight [J]. Chinese Journal of Agrometeorology,2008,29(2) :194-196. |
| [4] | 谢正文,孔凡玉. 基于熵技术的矿山安全模糊综合评价[J].中国计量学院学报, 2007,18(1):79-82.XIE Zheng-wen, KONG Fan-yu. Fuzzy Comprehensive Evaluation Method for Mines Based on Entropy Technology[J]. Journal of China Jiliang University, 2007,18(1):79-82. |
| [5] | 郝少峰,方源敏,杨建文,等.基于熵权法的组合模型在滑坡变形预测中的应用[J].测绘工程,2014,23(7):62-64.HAO Shao-feng, FANG Yuan-min, YANU Jian-wen, et al. Application of Combination Model of Entropy Method to Landslide Deformation Prediction[J].Engineering of Surveying and Mapping,2014,23(7):62-64. |
| [6] | 秦志斌,钱国平,马文彬.基于熵权的沥青路面使用性能多目标综合评价[J]. 中南大学学报:自然科学版,2013,44(8):3474-3478.QIN Zhi-bin, QIAN Guo-ping, MA Wen-bin. Multi-objective Comprehensive Evaluation for Performance of Asphalt Concrete Pavement Based on Fuzzy Entropy[J]. Journal of Central South University:Science and Technology Edition,2013.44(8):3474-3478. |
| [7] | 谢正文,胡汉华.基于熵权的灰色沉降组合预测模型及应用[J].矿业研究与开发,2007,27(4)12-13.XIE Zheng-wen, HU Han-hua. A Grey Combination Prediction Model for Settlement based on Entropy Weight and Its Application [J].Mining Research and Development,2007,27(4)12-13. |
| [8] | 张舒,史秀志,古德生,等. 基于ISM和AHP 以及模糊评判的矿山安全管理能力分析与评价[J]. 中南大学学报:自然科学版,2011,42(8):2406-2415.ZHANG Shu, SHI Xiu-zhi, GU De-sheng, et al. Analysis and Evaluation of Safety Management Capability in Mine Based on ISM and AHP and Fuzzy Evaluation Method[J]. Journal of Central South University: Science and Technology Edition, 2011,42(8):2406-2415. |
| [9] | ZHANG Wen-xiu. Incomplete Information System and Its Optimal Selections[J]. Computer and Mathematics with Applications,2010,48(5) : 691-698. |
| [10] | YANG Xi-bei, XIE Jun,SONG Xiao-ning,et al. Credible Rules in Incomplete Decision System Based on Descriptors[J]. |
| [11] | 吴顺详.灰色粗糙集模型及其应用[M].北京:科学出版社,2009.WU Shun-xiang. Gray Rough Set Model and Its Application[M]. Beijing: Science Press,2009. |
| [12] | 陈建宏,郑海力,刘振肖,等. 基于优势关系的粗糙集的巷道支护方案评价体系[J]. 中南大学学报:自然科学版,2011,42(6):1698-1703. CHEN Jian-hong,ZHENG Hai-li,LIU Zhen-xiao, et al. Rough Sets of Laneway Supporting Schemes Evaluation System Based on Dominance Relation[J]. Journal of Central South University:Science and Technology Edition,2011,42(6):1698-1703. |
| [13] | 罗凯,吴超,阳富强. 基于优势关系粗糙集与灰靶决策的矿石自燃管理应对体系[J].中南大学学报:自然科学版,2014,45(1):224-230. LUO Kai, WU Chao, YANG Fu-qiang. Management Response System to Ores Spontaneous Combustion Based on Dominance-based Rough Sets and Grey Target[J]. Journal of Central South University:Science and Technology Edition,2014,45(1):224-230. |
| [14] | 黄文雄.基于混合遗传神经网络的高速公路沥青路面使用性能评价方法研究[D].武汉:武汉理工大学,2003.HUANG Wen-xiong. Study on Performance Evaluation of Expressway Asphalt Pavement Based on Mixed GANN [D].Wuhan: Wuhan University of Technology,2003. |
| [15] | 曾胜.径向基函数网络在沥青路面使用性能评价中的应用[J].公路交通科技, 2008,25(3) :23-26.ZENG Sheng. Pavement Performance Evaluating Model by Using RBF [J].Journal of Highway and Transportation Research and Development,2008,25(3) :23-26. |
| [16] | 何铁军,黄卫.模糊神经网络在沥青路面使用性能评价中的应用[J]. 公路交通科技, 2000,17(4) :11-14.HE Tie-jun,HUANG Wei. Applicction of Fuzzy Neural Network in Bitumen Pavement Performance Assessment [J].Journal of Highway and Transportation Research and Development, 2000,17(4) :11-14. |
| [17] | 张云龙,刘茂.灰色GM(1,1)模型在火灾事故预测中的应用[J].南开大学学报:自然科学版,2009,42(1):11-15.ZHANG Yun-long, LIU Mao. Application of Grey Prediction Model GM(1,1) in Fire Accident[J]. Acta Scientiarum Naturalium Universitatis Nankaiensis,2009,42(1):11-15. |
| [18] | 郭丽萍,孙伟,郑克仁,等.非等时距GM(1,1) 直接模型及其在材料试验数据处理中的应用[J].东南大学学报:自然科学版,2004, 34(6):833-837.GUO Li-ping, SUN Wei,ZHENG Ke-ren, et al. Non-equal Interval GM(1,1) Direct Model and Its Application in Processing of Materials Experimental Data[J]. Journal of Southeast University :Natural Science Edition,2004, 34(6):833-837. |
| [19] | 周献中,黄兵,李华雄,等.不完备信息系统知识获取的粗糙集理论与方法[M].南京:南京大学出版社,2010.ZHOU Xian-zhong, HUANG Bing, LI Hua-xiong, et al. Rough Set theory and Method of Incomplete Information Systems Knowledge Acquisition[M]. Nanjing: Nanjing University Press,2010. |
| [20] | 程温鸣,彭令,牛瑞卿.基于粗糙集理论的滑坡易发性评价——以三峡库区秭归县境内为例[J]. 中南大学学报:自然科学版,2013,44(3):1083-1090.CHENG Wen-ming, PENG Ling, NIU Rui-qing. Landslide Susceptibility Assessment Based on Rough Set Theory: Taking Zigui County territory in Three Gorges Reservoir for example [J].Journal of Central South University:Science and Technology Edition, 2013,44(3):1083-1090. |
| [21] | 菅利荣.面向不确定性决策的杂合粗糙集方法及其应用[M].北京:科学出版社,2008.JIAN Li-rong. Uncertainty Decision-making Oriented Heterozygous Rough Set Method and Its Application [M]. Beijing:Science Press,2008. |
 2016, Vol. 31
2016, Vol. 31
