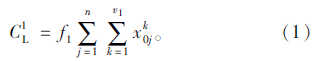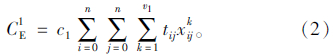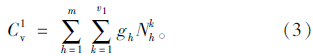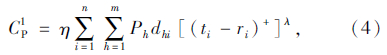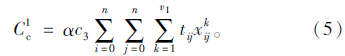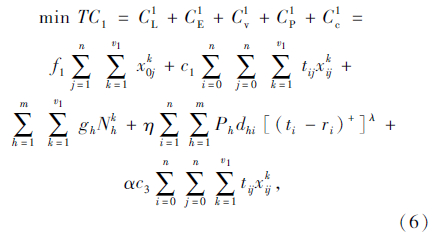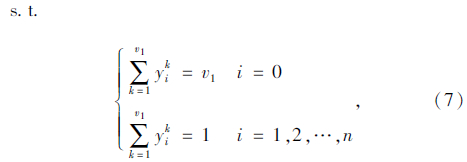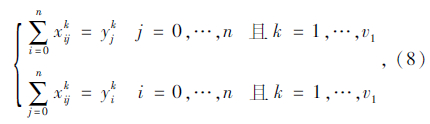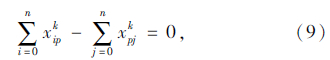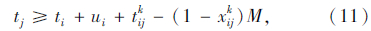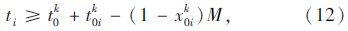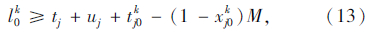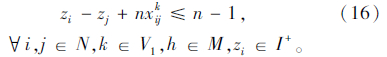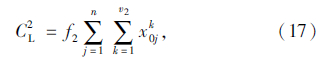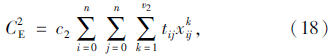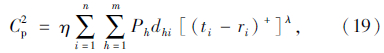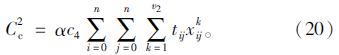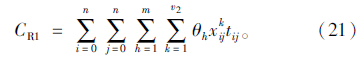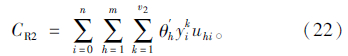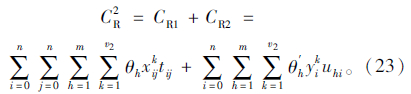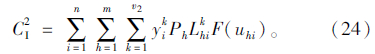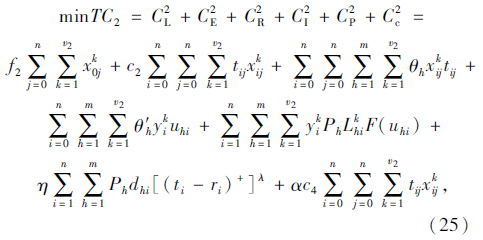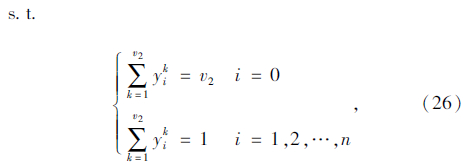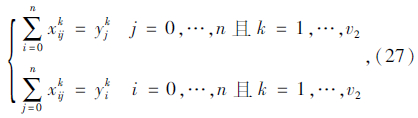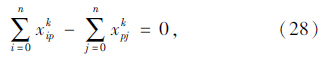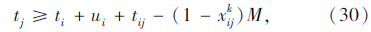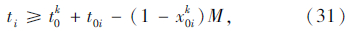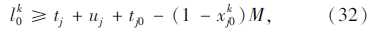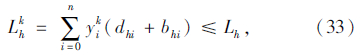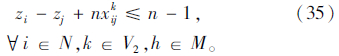扩展功能
文章信息
- 王淑云, 孙虹, 牟进进, 金辉
- WANG Shu-yun, SUN Hong, MOU Jin-jin, JIN Hui
- 冷链品多温共配优化及效益:基于蓄冷式和机械式的比较研究
- Optimization and Efficiency of Multi-temperature Joint Distribution of Cold Chain Products: Comparative Study Based on Cold Accumulation Mode and Mechanical Refrigeration Mode
- 公路交通科技, 2016, Vol. 33 (3): 146-153
- Journal of Highway and Transportation Research and Denelopment, 2016, Vol. 33 (3): 146-153
- 10.3969/j.issn.1002-0268.2016.03.024
-
文章历史
- 收稿日期: 2014-11-12
随着人们生活水平的提高、电子商务的快速发展,消费者对生鲜、冷冻等冷链品的需求量及种类不断增加,冷链品配送呈现出品种多样化、温度需求多层化的特点,冷链物流多温共配便应运而生。多温共配模式改善了传统单一品温配送的弊端,采用一车同时混装各种温层产品,且保证各温层需要的温度条件,旨在既保证产品品质、降低配送成本,缓解交通压力和减少环境污染,进而提升冷链配送的经济效益和环境效益。早在2006年,国际制冷学会就将多温共配运作策略、运输装备性能测试等视为优先研究的问题;剑桥制冷中心爵士Robert Heap在第22届国际制冷大会主题报告中进一步强调了冷链配送中食品安全与节能的重要性,并呼吁加强对多温共配的研究和推广利用。
目前,国内外常用的多温共配模式主要有机械式和蓄冷式两种。机械式多温共配模式使用机械冷冻区隔车辆进行配送,机械式冷冻车辆是在同一车厢用绝缘材料隔离出冷藏、冷冻等几种不同的温度区域,使用冷冻机分别控制每个区域的温度。蓄冷式多温共配模式用常温车和蓄冷保温箱进行配送,以创新设计的保温箱取代机械式冷冻车,利用可抽换、具有不同温度且以颜色区隔的蓄冷器保持保温箱中冷链品所需的温度条件,使用常温车辆即可同时配送各种温层的冷链品。
冷链品多温共配问题是传统单一冷链品配送问题的延伸,国内外有关单一冷链品配送的研究已很多,CHEN、AZI、BRITO、TAS、朱金峰、缪小红、石兆等国内外学者对单一冷链品的配送进行了较充分的研究[1, 2, 3, 4, 5, 6, 7]。在蓄冷式多温共配的研究中,CHO等总结台湾地区蓄冷保温箱的实践经验,论述了蓄冷式多温共配模式的可行性[8];KUO等综合分析食品冷链的框架体系,提出了多温共配的实施模式[9];HSU 等运用层级轴辐式网络,构建了以配送成本最小化为目标的多温共配优化路径模型,并通过算例证明了蓄冷式多温共配对少量多样冷链品配送的适应性[10];王淑云、HSU等通过与传统单品温配送模式的比较,论证了蓄冷式多温共配的经济性[11, 12]。在机械式多温共配模式的研究中,AHMED、ZWIERZYCKI、李锦等从多个角度对多温配送制冷系统进行了较为详尽的数值模拟和试验研究[13, 14, 15]。
相关研究及实践证明传统的机械式多温共配与新兴的蓄冷式多温共配都能够满足冷链品在配送过程中的温度要求和配送产品的品质保证。但以往的研究大多只针对多温共配的经济效益和性能,未将经济效益、安全性等因素考虑在内。然而随着低碳经济、食品安全性、交通拥堵等问题引起了全社会的高度关注,冷链物流企业在选择多温共配模式时,就必须综合考虑配送模式的经济性、环保性、安全性及灵活性等问题。本文充分考虑多温共配过程中所引起的固定成本、行驶成本、制冷成本、变质成本、保温箱成本、违反时间窗的惩罚成本和碳税成本,以配送总成本最小化为目标,分别构建蓄冷式和机械式多温共配的优化模型。随后,以实际算例,对两种模式的经济性、安全性、灵活性和环保性进行对比分析,旨在为冷链配送的运作管理提供理论支撑和实践指导。
1 问题描述与数学模型假设有一个配送中心分别运用蓄冷式多温共配模式和机械式多温共配模式为若干顾客配送冷链品,每个顾客的位置以及对不同种类冷链品的需求量已知,每个顾客都有时间窗要求,并且每辆车的容量已知。配送中心需确定车辆行驶线路,使得在满足车辆容量和时间窗限制下,实现配送成本最小化。
1.1 研究假设配送中心的车辆足够多,且用于同一多温共配模式的车辆规格完全相同;不考虑配送中心缺货,顾客的需求量、地理位置、时间窗已知;车辆由配送中心出发匀速行驶,服务被指定的顾客后,再返回配送中心;同一顾客的各类冷链品只能由一辆车同时送达,各类冷链品同时卸货,且卸货时间相同;冷链品需在保质期之内,且保证适宜温度配送,不考虑其他影响因素,冷链品的腐坏仅与卸货时间有关。
1.2 符号说明M={1,2,…,m}为冷链品种类集合;N={0,1,2,…,n}为顾客节点集合;V1={1,2,…,v1}为常温车辆集合;V2={1,2,…,v2}为机械式冷冻车辆集合。f1和f2分别为常温车辆和机械式冷冻车辆的固定成本;c1和c2分别为常温车辆和机械式冷冻车辆的单位行驶成本;c3和c4分别为常温车辆和机械式冷冻车辆单位时间的碳排放量;Lh为装载第h种冷链品的车厢容量;Lhk为第k辆车装载第h种冷链品的量,其中Lhk≤Lh;Lhik为车辆到达顾客i时车内的冷链品h剩余量;Ph为冷链品h的单位成本;dhi为顾客i对第h类冷链品的需求数量;uhi和ui分别为顾客i卸载冷链品h的时间和顾客i卸载冷链品的总时间;t0k为第k辆车从配送中心出发时间;l0k为第k辆车返回配送中心的时间;tijk为车辆k从顾客i开往顾客j的运输时间;ti为车辆到达顾客i的时间;[ei,ri,Ri]为顾客i的时间窗,最早允许的到达时刻为ei,最迟允许的达到时刻为Ri,其中,超过ri时刻需支付相应的惩罚成本;θh为机械式冷冻车辆行驶过程中,装有h类冷链品车厢单位制冷成本;θ′h 为装卸第h类冷链品过程中单位制冷成本;gh为用于装载第h类冷链品的蓄冷保温箱成本;b为每辆车最多可装载的蓄冷保温箱的数量;q为每个蓄冷保温箱可装载的冷链品总量;α为碳排放价格;F(uhi)为顾客i装卸冷链品过程中的变质比率;Nhk为整数变量,表示第k辆车中装载第h类冷链品所使用的蓄冷保温箱的数量;xijk为0-1变量,若第k辆车连续服务顾客i与顾客j则取1,否则取0;yik为0-1变量,表示顾客i的冷链品由第k辆车配送则取1,否则取0;zi为实数变量,避免产生子回路的变量。
2 模型构建 2.1 蓄冷式多温共配模型蓄冷式多温共配模式利用常温车搭配蓄冷保温箱进行配送,配送成本主要包括固定成本、行驶成本、保温箱成本、违反时间窗的惩罚成本以及碳税成本。
(1)固定成本
固定成本是派遣每辆配送车辆所担负的固定成本,包含配送车辆的固定损耗、驾驶员的工资等。蓄冷式多温共配使用常温车,每辆常温车的固定成本为f1,共需v1辆常温车为n个顾客配送冷链品,x0jk为0-1变量,若第k辆车从配送中心O出发后直接为顾客j服务,则取1,否则取0,则固定成本为:
(2)行驶成本
行驶成本包含配送车辆的油耗、保养等成本。由于配送车辆匀速行驶,行驶成本与行驶时间成正比。常温车单位时间的行驶成本为c1,配送车辆k从顾客节点i到顾客节点j的行驶时间为tij,则配送车辆的行驶成本为:
(3)保温箱成本
保温箱成本主要指蓄冷式保温箱的购买成本、加冷设备的使用成本以及保温箱的维修成本、保养费用等。每个蓄冷保温箱的成本为gh,则保温箱总成本为:
(4)惩罚成本
本研究采用软时间窗约束,即若配送车辆没有在指定的时间范围内到达,则导致一定的惩罚成本。根据Hsu等所构建的违反时间窗的惩罚成本模型[16],惩罚成本为:
其中η,λ为参数,且λ>1,ei≤ti≤Ri。
(5)碳税成本
通过对二氧化碳排放征税,可以实现环境保护。碳排放价格为α,常温车辆单位时间的碳排放量为c3,则碳税成本为:
综上所述,蓄冷式多温共配总成本为:
式(6)表示蓄冷式多温共配模式的目标函数,即配送总成本最小化;式(7)表示每个顾客仅被一辆车服务一次,且每条路线的起止点均为配送中心;式(8)表示每个顾客的流量守恒限制;式(9)表示只有一条最优化行驶路线;式(10)表示每辆车最多只能使用一次;式(11)车辆到达后一个顾客j的时间,大于到达前一个顾客i的时间与顾客i服务时间以及从顾客i到顾客j行驶时间之和;式(12)表示车辆到达第一个顾客i的时间,为车辆从配送中心出发的时间与配送中心到达顾客i行驶时间之和;式(13)表示车辆返回配送中心的时间,位于车辆服务完最后一个顾客j之后;式(14)表示时间窗限制;式(15)表示保温箱数量限制;式(16)表示变量的值域限制。
2.2 机械式多温共配模型机械式多温共配使用机械式冷冻车进行配送,配送成本主要由6部分组成:固定成本、行驶成本、制冷成本、变质成本、违反时间窗的惩罚成本以及碳税成本。其中固定成本、行驶成本、违反时间窗的惩罚成本和碳税成本与蓄冷式多温共配类似,分别为:
(1)制冷成本
机械式冷冻车辆的制冷成本主要是冷藏车辆为了保持冷链品所要求的相应温度而产生的制冷成本,一部分来源于车厢内外温差所造成的热传导,另一部分来源于卸货期间车门开启造成的热侵入。假设各机械式冷冻车辆的规格一致,不同时段的气温变化忽略不计。因此,制冷成本仅与冷链品运送的里程数和服务顾客的冷链品需求数量有关。在机械式冷冻区隔中,因为冷藏区和冷冻区内外温差不同,所以能耗成本包括两部分:冷藏区能耗成本和冷冻区能耗成本。因此,配送过程中的制冷成本可表示为:
在顾客点卸货时,打开车门进行操作过程中造成热量损失,制冷剂通过热交换而消耗,打开车门时的制冷成本表示为:
式中,uhi为卸货时间。综上,机械式多温共配的制冷成本为:
(2)变质成本
根据HSU等构建的配送模型[16],变质成本由两部分组成:一是配送累计时间导致的变质成本;二是因为卸货而开启车门,外界热空气进入车体导致车体内温度上升而造成的变质成本,本文忽略累计时间导致的变质成本。配送过程中变质成本表示为:
令bhi=LhikF(uhi),则bhi表示为节点i装卸所导致的h类冷链品变质数量。
综上所述,目标函数机械式多温共配总成本为:
式(25)为机械式多温共配的目标函数,即配送总成本最小化;式(26)表示每个顾客仅被一辆车服务一次,且每条路线的起止点均为配送中心;式(27)表示每个顾客的流量守恒限制;式(28)表示只有一条最优化行驶路线;式(29)表示每辆车最多只能使用一次;式(30)表示车辆到达后一个顾客j的时间,大于到达前一个顾客i的时间与顾客i服务时间以及从顾客i到顾客j行驶时间之和;式(31)表示车辆到达第一个顾客i的时间,为车辆从配送中心出发的时间与配送中心到达顾客i行驶时间之和;式(32)表示车辆返回配送中心的时间,位于车辆服务完最后一个顾客i之后;式(33)表示车辆的容量限制;式(34)表示时间窗限制;式(35)表示变量的值域限制。
3 配送路径优化蚁群算法(Ant Colony Optimization)是DORIGO等人于1991根据自然界中蚂蚁的觅食行为所提出的,是一种用来在图中寻找优化路径的启发式算法。蚂蚁在觅食过程中,会在食物与巢穴间所经过的路径上留下一种称为费洛蒙的特殊化学物质,蚂蚁觅食路径的选择主要由费洛蒙的浓度决定,此种方式有利于后续出发的蚂蚁决定是否依循此路径继续前进。通常,较短路径上的蚂蚁会较快觅食回巢,其留下的费洛蒙浓度较高,会吸引较多的蚂蚁依循此路径觅食。
本研究以DORIGO等所提出的ACS为基本架构[17],考虑VRPTW问题的限制条件,利用2-opt邻域搜索法作为蚁群算法的变异算子,对每条子路径进行优化,具体步骤如下:
(1)初始化变量和系数。
(2)每一只蚂蚁根据所构建的准则及车容量和时间窗的限制,依序产生一条配送路径,并且每只蚂蚁在完成配送路径之后,马上进行区域的费洛蒙更新。
(3)运用2-opt邻域搜索法,改善每一只蚂蚁所构建的配送路径。
(4)根据部分较佳蚂蚁所构建的配送路径,进行全域的费洛蒙更新。
4 算例及效益对比分析 4.1 算例描述某配送中心向31个顾客配送2种不同品温的冷链品,顾客的位置坐标(xi,yi)、需求量dhi及卸货时间uhi如表 1所示,其他参数值由表 2给出。配送车辆从配送中心O出发,以50 km/h的速度匀速行使,最后返回配送中心O。
| 节点i | 坐标 | dhi | 节点i | 坐标 | dhi | |||||
| x | y | h=1 | h=2 | x | y | h=1 | h=2 | |||
| 0 | 41 | 38 | 0 | 0 | 16 | 44 | 25 | 10 | 10 | |
| 1 | 48 | 22 | 5 | 10 | 17 | 45 | 1 | 25 | 5 | |
| 2 | 25 | 2 | 10 | 25 | 18 | 9 | 16 | 10 | 10 | |
| 3 | 24 | 4 | 15 | 10 | 19 | 46 | 1 | 25 | 5 | |
| 4 | 6 | 3 | 15 | 5 | 20 | 25 | 46 | 10 | 30 | |
| 5 | 14 | 44 | 5 | 10 | 21 | 49 | 7 | 5 | 10 | |
| 6 | 29 | 15 | 30 | 15 | 22 | 2 | 21 | 15 | 25 | |
| 7 | 42 | 19 | 15 | 25 | 23 | 21 | 4 | 10 | 5 | |
| 8 | 7 | 12 | 20 | 5 | 24 | 30 | 31 | 10 | 10 | |
| 9 | 1 | 19 | 10 | 35 | 25 | 4 | 48 | 20 | 25 | |
| 10 | 1 | 41 | 5 | 10 | 26 | 40 | 27 | 10 | 15 | |
| 11 | 2 | 5 | 10 | 5 | 27 | 28 | 34 | 15 | 25 | |
| 12 | 49 | 26 | 20 | 5 | 28 | 11 | 7 | 10 | 10 | |
| 13 | 42 | 12 | 15 | 10 | 29 | 10 | 35 | 35 | 20 | |
| 14 | 30 | 29 | 10 | 20 | 30 | 42 | 30 | 10 | 15 | |
| 15 | 0 | 32 | 5 | 15 | 31 | 49 | 2 | 15 | 5 | |
| 参数 | 参数值 | 参数 | 参数值 | |
| f1/元 | 100 | Ph/元 | 15/25 | |
| f2/元 | 120 | Lh | 90/90 | |
| c1/c2/元 | 50/50 | θh/元 | 5/10 | |
| c3/( kg·h-1) | 15 | θ′h/元 | 10/20 | |
| c4/( kg·h-1) | 30 | α/(元·kg-1) | 0.03 | |
| b/个 | 32 | [ei,ri,Ri] | [0,180,210] | |
| q | 5 | Fhi | 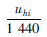 | |
| gh/元 | 1/1 | |||
| uhi/min | 10/10 |
运用蚁群算法,在Matlab中运行,使用蓄冷式多温共配和机械式多温共配2种模式得出的运行路径如表 3和表 4所示。
| 路径 | |
| 第1条 | 0—7—1—12—16—26—30—0 |
| 第2条 | 0—2—3—23—28—4—11—8—0 |
| 第3条 | 0—29—10—25—5—0 |
| 第4条 | 0—6—18—9—22—15—0 |
| 第5条 | 0—13—17—19—31—21—0 |
| 第6条 | 0—14—27—20—0 |
| 路径 | |
| 第1条 | 0—12—1—16—26—30—0 |
| 第2条 | 0—2—3—23—4—8—18—0 |
| 第3条 | 0—5—25—10—15—29—0 |
| 第4条 | 0—6—28—11—9—22—0 |
| 第5条 | 0—7—13—21—31—19—17—0 |
| 第6条 | 0—14—24—27—20—0 |
将算例中的数据分别代入蓄冷式多温共配和机械式多温共配2种模型,得到2种模型的总成本以及固定成本、行驶成本等,如表 5所示。
| 配送模式 | 固定成本 | 行驶成本 | 制冷成本 | 变质成本 | 保温箱成本 | 碳税成本 | 总成本 |
| 蓄冷式 | 600.00 | 485.49 | — | — | 168.00 | 4.37 | 1 257.86 |
| 机械式 | 720.00 | 496.43 | 249.24 | 242.80 | — | 8.94 | 1 717.41 |
下面分别从经济性、安全性、灵活性和环保性带来的效益进行分析。
(1)经济性分析
根据表 5,两种模式的比较分析,发现:
蓄冷式多温共配的总成本低于机械式多温共配。机械式的总成本比蓄冷式高459.55元,分析表 3、表 4和表 5中的路径和成本明细可知,两种模式的配送路径数量相同,但由于机械式多温共配需要使用专门的机械式冷冻车,致使其固定成本高于蓄冷式多温共配模式。而且使用机械式冷冻车配送需不间断制冷,在卸货过程中会产生车厢内外的热交换,致使其产生额外的制冷成本和变质成本。
保温箱的重复循环使用大大提高了蓄冷式配送的经济性。由表 5可知,蓄冷式多温共配需额外支付168元的保温箱成本,这是由于蓄冷式多温共配使用常温车配送,需要利用保温箱来维持冷链品所需的特定温度。
为了进一步分析保温箱成本对蓄冷式多温共配模式选择的影响,现令其他常规设施成本不变,假设单位保温箱成本gh为一变量,其他参数值已知,如表 2所示。为了求得单位保温箱成本gh的临界值,令TC1=TC2,即蓄冷式多温共配总成本等于机械式多温共配的总成本,将算例中的已知数据代入求得gh=3.70。即:当保温箱成本gh<3.70元时,蓄冷式多温共配的总成本低于机械式多温共配;当保温箱成本gh>3.70元时,蓄冷式多温共配的总成本高于机械式多温共配。根据台湾冷链配送实践,单位的可循环、重复使用的蓄冷保温箱成本都在1元之内[12]。为此,虽然使用蓄冷式多温共配需支付额外的保温箱成本,但其随着蓄冷保温箱的重复循环使用其经济效益更加突出。
(2)安全性分析
蓄冷式配送的恒温性更易于保证冷链品品质及食用安全。由表 5知,在机械式多温共配中,由于卸货过程中的开关门所导致的变质成本为242.80元,与之对应的便是冷链品品质的下降,对温度条件要求苛刻的冷链品的影响更甚。而蓄冷式多温共配利用蓄冷器和保温箱维持冷链品所需的温度调节,箱内温度基本不受开启车门影响,有效避免了机械式冷冻车在装卸作业中的冷度流失,能够维持冷链品温度需求的恒定性,这样就可以保证冷链品的产品品质和食用的安全性。
持久的均温性在保持冷链品品质的同时,易于延长冷链品的配送半径。在冷链物流中,配送耗时也是影响产品保质期和最终质量的重要因素。与机械式配送模式相比,“交通拥堵、装卸车所用时间、开门次数以及其他不可预测的随机干扰在带来冷链品冷度流失的同时,也会带来配送时间的拉长,进而降低冷链品的鲜度甚至食用安全。蓄冷式多温共配采用冷融材料高的蓄冷器制冷,替代了车引擎驱动冷冻机组制冷,均温性高,且箱内温度可以维持12 h之久。持久的均温性,不仅使得配送半径达到近千里,也保证了冷链品的品质和食用安全性”[18]。
蓄冷保温箱的使用易于避免断链问题。在意外交通情况下,蓄冷保温箱里的货物可以很容易地转卸至适用型号车辆,基本可以保证在任何路况的畅通配送,很好地避免了可能的断链问题,大大提高了交通路况的配送柔性,并有效地保证了产品品质,减少了配送过程中的资源浪费。
综上,无论从冷链温度、配送时间还是交通状况,蓄冷式多温共配都利于保证产品的品质和安全性。
(3)灵活性分析
机械式多温共配使用机械式冷冻车,各个温层的空间比例通常是固定不变的,如上述算例中2个温层的比例为1∶1。算例中每个顾客对两种冷链品的需求总量都为420,比例为1∶1,与机械式冷冻车两个温层的比例相同。然而,不同种类冷链品的需求比例通常会因季节、气候等因素的变化而变动。在两种冷链品需求总量及其他参数值不变的条件下,将每个顾客的第1种冷链品的数量减少5单位,第2种冷链品的数量分别增加5单位,即第1种冷链品的需求总量变为265,第2种冷链品的需求总量变为575,运用蚁群算法重新规划配送路径,结果是蓄冷式多温共配配送路径不变,见表 3。但机械式多温共配路径发生了很大变化,其配送路径由6条增加到8条,如表 6所示。
| 路径 | |
| 第1条 | 0—12—1—16—26—0 |
| 第2条 | 0—3—2—4—11—18—0 |
| 第3条 | 0—5—25—10—0 |
| 第4条 | 0—6—17—19—31—21—0 |
| 第5条 | 0—7—13—23—28—8—0 |
| 第6条 | 0—9—22—15—0 |
| 第7条 | 0—14—24—27—0 |
| 第8条 | 0—20—29—30—0 |
将数据分别代入蓄冷式多温共配和机械式多温共配两种模型,发现蓄冷式配送成本不变,但调整后的机械式多温共配成本大幅上升,配送成本由1 717.41 元提高到2 091.99元 ,增长率达21.8%,如表 7所示。
通过表 6和表 7,发现:
| 配送模式 | 固定成本 | 行驶成本 | 制冷成本 | 变质成本 | 变动成本 | 碳税成本 | 总成本 | |
| 调整前 | 蓄冷式 | 600.00 | 485.49 | — | — | 168.00 | 4.37 | 1 257.86 |
| 机械式 | 720.00 | 496.43 | 249.24 | 242.80 | — | 8.94 | 1 717.41 | |
| 调整后 | 蓄冷式 | 600.00 | 485.49 | — | — | 168.00 | 4.37 | 1 257.86 |
| 机械式 | 960.00 | 646.86 | 305.82 | 167.67 | — | 11.64 | 2 091.99 |
确定情况下,蓄冷式多温共配具有更高的空间灵活性。由于蓄冷式多温共配不受冷链品种类限制,只需将不同温层的冷链品放入适宜温度的保温箱,即可同一车辆共同配送,无论不同品温需求比例如何变化,总成本都保持不变,如表 7所示,这充分体现了蓄冷式多温共配的空间灵活性。而机械式多温共配受各个温层空间的限制、灵活性差,若客户整体对某一温层冷链品的需求过多或过少,将致使机械式冷冻车的空间利用率进一步降低进而增加配送路径以及大幅度提升配送成本,如表 6和表 7所示,其结果无法体现多温共配的实质和精髓。
随机情况下,蓄冷式多温共配的装载弹性更加突出。本算例仅对顾客需求确定、配送时间确定的情况下,两种冷链品的配送模式进行了比较研究,若推广到顾客需求不确定、配送时间不确定、2种以上冷链品的共同配送情形,将更凸显出蓄冷式多温共配不受品类限制、不受时间限制(12 h以内)的装载空间灵活性及由此带来的经济优越性。
(4)环保性分析
蓄冷式多温共配有效地降低了环境污染。与机械式多温共配相比,蓄冷式多温共配不需要配备冷冻动力,只需将蓄冷器放入保温箱即可制冷,由表 5所示,蓄冷式多温共配避免了制冷成本和变质成本并降低了碳税成本,所有这些都减少了来自机械制冷或电力制冷带来的碳排放及产品腐坏产生的环境污染。机械式多温共配则需要在配送过程中不间断制冷,这势必会造成环境污染、噪音污染,并破坏城市环境。
蓄冷式多温共配可减少资源浪费。由表 5知,在机械式多温共配中,由于卸货过程中的开关门所导致的变质成本为242.80元,这意味着冷链品品质的下降及带来资源浪费。而蓄冷式多温共配的安全性,保证了冷链品的保质保值,避免了任何因食品变质而带来的资源浪费。此外,在意外交通情况下,使用蓄冷保温箱所避免的断链问题,不仅提高了交通路况的配送柔性,也减少了冷链品的腐坏变质,进而减少资源浪费。
5 结论本研究通过对考虑碳排放的蓄冷式多温共配与机械式多温共配2种模式的建模、配送路径优化及算例对比分析发现,蓄冷式多温共配在经济性、安全性、灵活性和环保性等效益方面均优于机械式多温共配。具体体现在:蓄冷式多温共配的总成本低于机械式多温共配,而且随着蓄冷式保温箱的重复循环使用更加强化了蓄冷式配送的经济性;蓄冷式配送的恒温性以及持久的均温性,既易于保证冷链品品质及食用安全,又利于延长冷链品的配送半径并避免任何断链问题;无论在确定情况下还是在随机情况下,蓄冷式多温共配均具有更高的空间灵活性和不可比拟的装载弹性。我国大陆要充分借鉴台湾地区的蓄冷式多温共配技术,积极发展蓄冷式多温共配以更好地实现冷链物流的低碳节能、冷链产品的保质保值和配送半径的延伸扩展。一方面,要发挥政府的推动和政策激励作用;另一方面,服务业者要积极寻求由机械式配送到蓄冷式配送的转变。另外,本研究在建模、配送路径优化及算例分析中,只考虑了静态环境下单配送中心的冷链品配送优化,未来的理论与方法研究可扩展到动态环境下需求量/配送时间不确定的多场站多温共配问题。
| [1] | CHEN H K, HSUEH C F, CHANG M S. Production Scheduling and Vehicle Routing with Time Windows for Perishable Food Products[J]. |
| [2] | AZI N, GENDREAU M, POTVIN J Y. An Exact Algorithm for a Vehicle Routing Problem with Time Windows and Multiple Use of Vehicles[J]. |
| [3] | BRITO J, MARTINEZ F J, MORENO J A, et al. Fuzzy Optimization for Distribution of Frozen Food with Imprecise Times[J]. |
| [4] | TAS D, DELLAERT N, VAN WOENSEL T, et al. Vehicle Routing Problem with Stochastic Travel Times Including Soft Time Windows and Service Costs[J]. |
| [5] | 朱金峰. 城市冷链物流车辆路径模型优化研究[D]. 济南:山东师范大学, 2007. ZHU Jin-feng. Optimization Research on Vehicle Routing Problem of City Cold Chain Logistics[D].Jinan:Shandong Normal University, 2007. |
| [6] | 缪小红, 周新年, 林森, 等. 第3方冷链物流配送路径优化研究[J]. 运筹与管理,2011,20(4):32-38. MIAO Xiao-hong, ZHOU Xin-nian, LIN Sen, et al. Study on Routing Optimization for Cold-chain Logistics Distribution of 3PL[J]. Operations Research and Management Science, 2011,20(4):32-38. |
| [7] | 石兆, 符卓. 时变网络条件下带时间窗的食品冷链配送定位-运输路径优化问题[J].计算机应用研究,2013,30(1):183-188. SHI Zhao, FU Zhuo. Distribution Location Routing Optimization Problem of Food Cold Chain with Time Windows in Time Varying Network[J]. Application Research of Computers, 2013,30(1):183-188. |
| [8] | CHO Y J, LI C C. Application of Multi-temperature Refrigerated Container to Improve the Distribution of Cold Logistics[J]. Journal of the Eastern Asia Society for Transportation Studies,2005,6:2794-2808. |
| [9] | KUO J C, CHEN M C. Developing an Advanced Multi-temperature Joint Distribution System for the Food Cold Chain[J]. |
| [10] | HSU C I, LIU K P. A Model for Facilities Planning for Multi-temperature Joint Distribution System[J]. |
| [11] | 王淑云, 赵敏. 蓄冷式冷链物流多温共配的动力机制[J].公路交通科技,2012,29(2):144-148,158. WANG Shu-yun, ZHAO Min. Impetus of Multi-temperature Joint Distribution Based on Storage-type Cold-chain Logistics[J]. Journal of Highway and Transportation Research and Development, 2012,29(2):144-148,158. |
| [12] | HSU C J, CHEN W T. Optimizing Fleet Size and Delivery Scheduling for Multi-temperature Food Distribution[J]. |
| [13] | AHMED M, MEADE O, MEDINA M A. Reducing Heat Transfer Across the Insulated Walls of Refrigerated Truck Trailers by the Application of Phase Change Materials[J]. |
| [14] | ZWIERZYCKI W, BIENCZAK K, BIENCZAK M, et al. Thermal Damage to the Load in Cold Chain Transport[J]. |
| [15] | 李锦, 谢如鹤, 刘广海, 等. 多温冷藏车降温特性及其影响参数研究[J]. 农业机械学报,2013,44(2):128-135. LI Jin, XIE Ru-he, LIU Guang-hai,et al. Cooling Characteristics and Influence Parameters of Multi-temperature Refrigerated Truck[J].Transactions of the Chinese Society for Agricultural Machinery, 2013,44(2):128-135. |
| [16] | HSU C I,HUANG S F, LI H C. Vehicle Routing Problem with Time-windows for Perishable Food Delivery[J]. |
| [17] | DORIGO M,GAMBARDELLA L M. Ant Colony System:A Cooperative Learning Approach for the Traveling Salesman Problem[J]. |
| [18] | 王倩, 王淑云. 关于发展蓄冷式冷链物流多温共配的思考[J]. 中国海洋大学学报:社会科学版,2012(5):49-54. WANG Qian, WANG Shu-yun. Reflections on the Development of Multi-temperature Joint Distribution Based on Storage Cold Chain Logistics[J]. Journal of Ocean University of China:Social Sciences Edition, 2012(5):49-54. |
 2016, Vol. 33
2016, Vol. 33