扩展功能
文章信息
- 贺政纲, 邹晔, 杨晓
- HE Zheng-gang, ZOU Ye, YANG Xiao
- 报废汽车物流网络选址-路径问题建模与求解算法研究
- Research of Modeling and Algorithm for ELV Logistics Network Location-routing Problem
- 公路交通科技, 2016, Vol. 33 (3): 138-145
- Journal of Highway and Transportation Research and Denelopment, 2016, Vol. 33 (3): 138-145
- 10.3969/j.issn.1002-0268.2016.03.023
-
文章历史
- 收稿日期: 2015-03-19
2. 宜宾职业技术学院 五粮液技术学院, 四川 宜宾 644003
2. Wuliangye Technology Institute, Yibin Vocational and Technical College, Yibin Sichuan 6444003, China
报废汽车资源化具有巨大的经济价值和资源环境价值。在报废汽车回收物流网络中,其结构如图 1所示,拆解中心和中转场的两级选址-路径决策将对整个网络的运作效率与效益有重大影响,进而影响报废汽车的回收利用率。

|
| 图 1 报废汽车回收物流网络结构 Fig. 1 Structure of ELVs recycling logistics network |
赵佳虹等构建了一个危险废物回收物流系统选址-路径问题的多目标改进模型。该模型特别考虑了废物类型与运输车辆的多样性,废物与运输车辆的相容性,并采用暴露人口吨数表示风险,以最小化最大风险区域代表风险公平性优化目标。同时,该模型主要确定了回收中心的位置,回收中心配备的运输车辆类型,以及各类危险废物的车辆运输路径[1]。闻轶对LRP问题进行了多目标优化,以最短时间、客户需求和最小成本为目标建立了多目标随机优化模型,随机性在于论文考虑了客户需求的不确定性、车辆行驶时间的不确定性、以及车辆载重约束等影响因素[2]。张长星对选址-路径问题的算法进行了研究分析,设计了改进遗传算法求解LRP问题[3]。曾庆成等建立了物流配送系统网络优化的双层规划模型。配送中心的选址问题为模型上层,车辆路径优化问题为模型下层。先由上层选址模型给出初始配送中心选址方案,在此基础上再由一下层VRP模型获得最优车辆路径,然后计算上层选址模型中的供应商到已选配送中心的运输成本,构成系统模型目标函数,通过对目标函数的优化过程再对上层选址模型方案进行调整[4]。张潜对LRP问题中的选址配给、路径优化、选址-路径优化3类问题的具体优化算法进行了分析和比较,并提出采用两阶段启发式算法来求解LRP问题[5]。
1 模型构建 1.1 模型描述报废汽车回收物流网络选址-路径问题主要包括:(1)拆解中心选址问题。拆解中心的选址尽可能满足:远离居民区、学校等民用建筑;尽可能靠近中转量大的中转场。(2)中转场选址问题。中转场的选址尽可能满足:回收点到相应的中转站距离最短;报废汽车数量多的回收点尽可能靠近中转站。(3)拆解中心和中转场的建设数目。在模型构建中考虑拆解中心和中转站本身的建设费用。(4)车辆路径问题。车辆路径包括收集车辆及运输车辆的路径问题,需解决收集车辆在每一个周期内的运行路线。
报废汽车回收物流系统可看作由集合G=(V,E) 表示的一个网络图。V为节点位置,V={o|o=1,2,…,p,p+1,p+2,…,p+n,p+n+1,p+n+2,…,p+n+m};节点 H={h|h=1,2,…,p} 为拆解中心候选点的位置; J={j|j=1,2,…,n} 为中转场候选点的位置; I={i|i=1,2,…,m} 为m个回收点的位置。
报废汽车回收物流系统中,共配备两种车型,一种是从回收站点将收集到的废旧汽车运往中转场的收集车辆;另一种是从中转场大批量运送废旧汽车到拆解中心的运输车辆。
报废汽车回收物流网络中选址-路径问题属于两级设施选址、多车型回收并包含车辆载重约束、设施容量约束、无时间窗的LRP问题。选址-路径优化模型构建的目标是使得整个系统的固定投资和周期内的运行成本之和最小,即拆解中心和中转场的建设成本、收集车辆的收集成本及运输车辆的运输成本之和最小。
1.2 模型假设模型的前提假设:(1)拆解中心和中转场候选点的数目、位置及建设费用已知;(2)回收点数目、位置及日回收量已知;(3)每个回收点的报废汽车仅由一辆收集车辆进行收集,车辆运载量不得超过其最大载重,且同类型的车辆最大载重相同;(4)假定车辆在每条路径上行驶的最长时间为1 d;(5)每条路径上回收点的报废汽车收集量小于或等于收集车辆的额定载重;(6)每辆收集车辆的始发点和终点为同一中转场或拆解中心,且只负责一次收集活动;(7)拆解中心具有中转场的全部功能,即拆解中心是一个特殊的中转场,故拆解中心可越级收集报废汽车;(8)车辆收集和运输成本与运输距离和运量成正比;(9)道路状况稳定,不考虑交通堵塞问题或车辆本身故障情况,车辆恒速稳定运行;(10)拆解中心建成后的使用年限为M年,中转场建成后的使用年限为N年。
模型符号假设: H={h|h=1,2,…,p} 为拆解中心候选点集合;J={j|j=1,2,…,n}为中转场候选点集合; I={i|i=1,2,…,m}为回收点集合; U=H∪I为拆解中心和回收点的集合;W=H∪J为 拆解中心和中转场的集合;O=I∪J为中转场和回收点的集合;V=H∪J∪I为拆解中心、中转场和回收点的集合; K={k|k=1,2,…,a} 为收集车辆集合; S={s|s=1,2,…,b}为运输车辆集合;fh为拆解中心候选点h的建设费用;fj为中转场候选点j的建设费用;gh为拆解中心h拆解单位报废汽车的成本;gj为中转场j处理单位报废汽车的成本;ca为收集车辆的单位距离行驶费用;cb为运输车辆的单位距离行驶费用;ph为拆解中心h的拆解能力;pj为中转场j的中转能力;Qa为收集车辆的额定载重量;Qb为运输车辆的额定载重量;M为拆解中心建成后的使用年限;N为中转场建成后的使用年限;qi为回收点i的日报废汽车收集量;dij为从点i到点j的直线距离(其中i∈V,j∈V);djh为从点j到点h的直线距离;dih为从点i到点h的直线距离;Yh=1为在h处建立拆解中心,否则Yh=0; Yj=1为在j点建立中转场,否则Yj=0;Xihk=0为从i点到j点的报废汽车由收集车辆k负责收集,否则Xihk=0;Xihk=1为从i点到h点的报废汽车由收集车辆k负责收集,否则Xihk=0;Zhjs=1为第j(j∈J)个中转场的废旧汽车由运输车辆s运送至拆解中心h,否则Zhjs=0。
1.3 模型建立
由于拆解中心成本F1主要指拆解中心建设成本与拆解成本,成本为: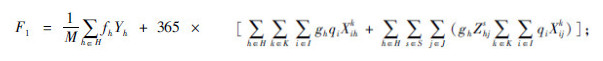 中转场成本主要指中转场建设成本与中转成本,中转场成本为:
中转场成本主要指中转场建设成本与中转成本,中转场成本为: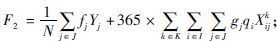 收集车辆年运行成本为
收集车辆年运行成本为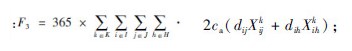 运输车辆年运行成本为:
运输车辆年运行成本为:
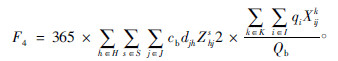
故模型构建如下:
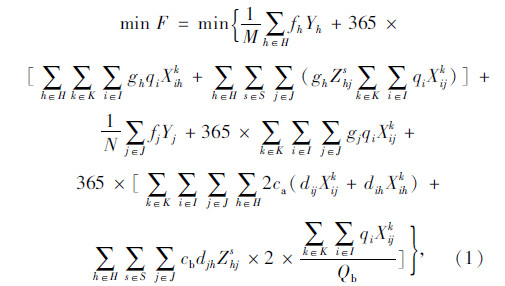
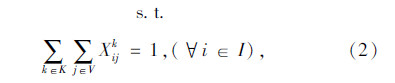
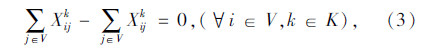
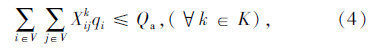
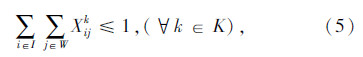
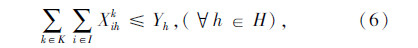
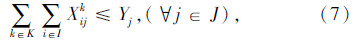
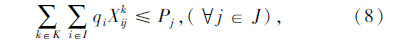
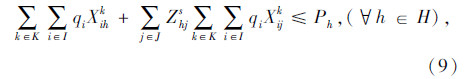
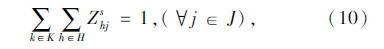
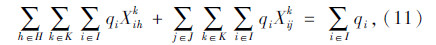
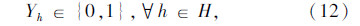
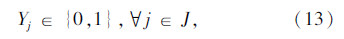
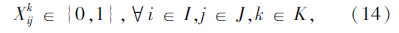

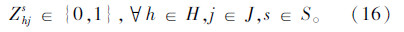
上述式(1)表示总目标函数,即中转场和拆解中心建设及运行成本、各节点间运输成本之和最小;式(2)表示每个回收点仅由一辆收集车辆负责收集;式(3)表示路径连续性约束,即到达任何节点的车辆必须离开该节点;式(4)表示收集车辆最大载重约束;式(5)表示每辆收集车辆在每条收集路径上只经过一个拆解中心或中转场,并保证拆解中心或中转场的每一辆收集车辆都能投入运行;式(6)表示拆解中心一旦为某个回收点服务,该拆解中心一定建设;式(7)表示中转场一旦为某个回收点服务,该中转场一定建设;式(8)表示中转场容量约束;式(9)表示拆解中心容量约束;式(10)表示每个中转场只能被运输车辆访问一次;式(11)表示从回收点运往中转场的报废汽车和回收点运往拆解中心的报废汽车的总和等于回收点的回收量;式(12)~式(16)为决策变量0-1取值约束。
2 算法设计针对遗传算法和禁忌搜索算法各自的搜索不足,文章将构造遗传算法和禁忌搜索的组合算法。采用两阶段算法进行求解:第一阶段进行中转场选址,按照实际问题结合已构建的数学模型初始化问题,设计遗传算法算子以及禁忌搜索算法的参数。其次设定遗传算法和禁忌搜索算法之间的结合条件,规定结合点。执行遗传搜索,在遗传搜索的过程中判定是否满足禁忌搜索的条件,若满足,则进行禁忌搜索,否则继续进行遗传搜索,最终输出最优解。第二阶段在中转场已选的基础上进行拆解中心选址。
2.1 算法设计要素(1)编码
选址-路径问题的解包括四部分内容:选址、分派、车辆分配、路径选择,文章拟采用非定长实数编码方式。①对候选拆解中心、候选中转场、回收站点、车辆进行编号,利用编号进行编码;②根据解的特点构建染色体,染色体的长度各不相等,但所有染色体均由3个子串构成。其中子串3表示各回收点的排列顺序;子串1和子串3一一对应表示为各回收点服务的车辆编号;子串2表示的是子串1中车辆归属的中转场的编号。具体编码过程参照以下实例:现已知收集车辆4辆,编号1,2,3,4;回收点10个,编号4,5,…,14;3个中转场,编号1,2,3;拆解中心2个,编号为4,5。具体编码如下:

其中子串1中1,2,3,4车辆都有,表示没有多余车辆,每辆车都得到合理利用。另外子串1中基因位1,6,7均为1,一一对应的子串3中回收点10,9,13,表示由车辆1按照10-9-13的顺序回收。同理,车辆2按12-8-14的顺序进行回收,车辆3按6-7-11的顺序回收,车辆4单独对回收点5进行回收。子串2按照3-1-4-2的顺序排列,表示车辆1,2,4分别归属于中转场和拆解中心3,1,2,车辆3归属于拆解中心4。
(2)初始化种群
设种群规模为num,随机产生初始种群,方法如下:随机产生一条染色体,判断是否满足车辆容量和中转场容量的限制。若满足,即为可行解,否则另外产生一条染色体,直到产生num条可行染色体为止。其具体的生成步骤如下:①设置种群规模为m。②从待选拆解中心和中转场中随机选择3个作为已选物流节点。③对已选的3个物流节点进行分派,分别计算ru,riu(ru表示拆解中心或中转场与其他拆解中心或中转场之间的最短距离的一半,riu表示客户点与拆解中心或中转场之间的距离)。④判定是否riu≤ru,若是,则将客户点i分配给拆解中心或中转场u;否则,将客户点i分配给距离最近的拆解中心或中转场。⑤已选拆解中心或中转场u从分派的回收点中随机选择产生一条新路径,判定该路线的运载量超限与否,若不超限,继续随机选择客户点插入路线,累加路线的总回收量;否则,进行调整。⑥所有回收站点均加入路线中,并且均满足车容量和场站容量限制,得到一个初始解。
(3)适应度函数
令适应度函数为fi=Zmin/Zl,其中fi为染色体l的适应度函数值;Zmin为同一代染色体中目标函数值的最小值;Zl为第l条染色体的目标函数值。故适应度函数值取值范围为0,1]。
(4)选择操作
采用轮盘赌选择和精英保留相结合的选择策略。①采用精英保留策略。每次生成下一代种群时,先将父代种群以及交叉、变异操作产生的临时种群中的最优个体直接复制进入下一代种群;②对除精英外的其他个体的适应函数值求和,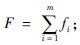 ③对除精英以外的染色体分别进行选择概率计算,
③对除精英以外的染色体分别进行选择概率计算,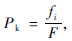 i=1,2,…,m;④以概率分布Pk从除精英外的上一代种群p(t)中随机选择染色体和精英染色体一起构成新一代种群 p(t+1)。
i=1,2,…,m;④以概率分布Pk从除精英外的上一代种群p(t)中随机选择染色体和精英染色体一起构成新一代种群 p(t+1)。
(5)交叉和变异操作
①选择交叉操作的概率 Pc,并生产伪随机数rk[rk∈(0,1),k=1,2,…,n],若rk<Pc,则选择Vk作为父代,然后随机配对选择出的父代(Vi,Vj); ②选择父代Vi和Vj 的子串1和子串2进行单点交叉和两点交叉操作,同时进行对换变异操作;子串3采用顺序交叉和部分匹配交叉操作,并进行逆转变异操作。
(6)禁忌搜索操作
①设定遗传算法迭代过程中,每隔N代对种群中所有染色体执行禁忌搜索算法(设迭代步数为IN,每次迭代共搜索当前解的NS个邻近解,禁忌长度为TL),之后继续执行遗传算法。②在遗传算法计算过程中若当前最优解连续保持L代不变,也对其执行禁忌搜索算法(设迭代步数为IN′,每次迭代共搜索当前解的NS′个邻近解,禁忌长度为TL′),之后继续执行遗传搜索。③当前最优解已连续保持2×L代不变,则对其再次执行禁忌搜索算法,之后继续执行遗传算法。④当前最优解已连续保持3×L代不变,则终止遗传/禁忌混合算法。
2.2 算法求解步骤Step 1:初始化问题。
Step 2:设置遗传算法的种群规模num和最大迭代次数maxgen,交叉概率Pc,变异概率Pm和禁忌搜索算法的参数N,L。
Step 3:生成种群规模为num的初始种群;设遗传算法的当前进化代数gen=0。
Step 4:计算初始种群中每个个体的目标函数值和适应度函数值。
Step 5:将初始种群的最优目标函数值best作为当前最优目标函数值bestnew,记录当前最优解连续保持代数β=0。
Step 6:若β=3L,转Step 16;否则,转Step 7。
Step 7:若β<L,转Step 9;否则,转Step 8。
Step 8:若β%L≠0,转Step 9。否则,对当前最优解执行禁忌搜索算法,将当前种群的最优目标函数值best和bestnew进行比较,若best<bestnew,令bestnew=best,β=0,转Step 9;否则,直接转Step 9。
Step 9:若gen%N=0,对当前种群中所有染色体执行禁忌搜索算法,转Step 10;否则,直接转Step10。
Step 10:采用轮盘赌选择和精英保留策略相结合的选择策略选择染色体。
Step 11:采用替代策略使用种群中最优的染色体替代种群中适应能力较差的个体。
Step 12:按照交叉概率Pc,两两配对执行交叉操作。
Step 13:按照变异概率Pm,在种群中选择进行变异的个体执行变异操作。
Step 14:令gen=gen+1,计算当前种群中每个个体的目标函数值和适应度函数值。将当前种群的最优目标函数值best和bestnew进行比较,若best<bestnew,令bestnew=best,β=0;否则,令β=β+1。
Step 15:若gen>maxgen,转Step 16;否则,转Step 6。
Step 16:算法结束,输出结果。
以上算法步骤中禁忌搜索算法的具体步骤如下:
Step 1:在遗传搜索过程生产的最优解中产生初始解。
Step 2 :令禁忌表为空,制定禁忌长度L及迭代次数StopL。
Step 3:令初始解为当前解和bestnew。
Step 4:若p<StopL,执行Step 5,若否,输出结果;其中,p为当前迭代次数。
Step 5:设计邻域产生策略。
Step 6:产生当前解的25个邻域解。
Step 7:将这25个邻域解进行从小到大的排序。
Step 8:选出其中前面10个邻域解作为候选解。
Step 9:若best<bestnew,令bestnew=best,更新禁忌表,当前解对应的禁忌对象的禁忌长度为n,禁忌表中其他对象分别减1;若否,转Step 12。
Step 10:若该解的禁忌对象的禁忌长度≠0,排名第一的候选解被删除,排名第二的候选解成为排名第一,转Step 13;若否更新当前解;更新禁忌表,当前解对应的禁忌对象的禁忌长度为n,禁忌表中其他对象分别减1。
Step 11:p=p+1转step 4。
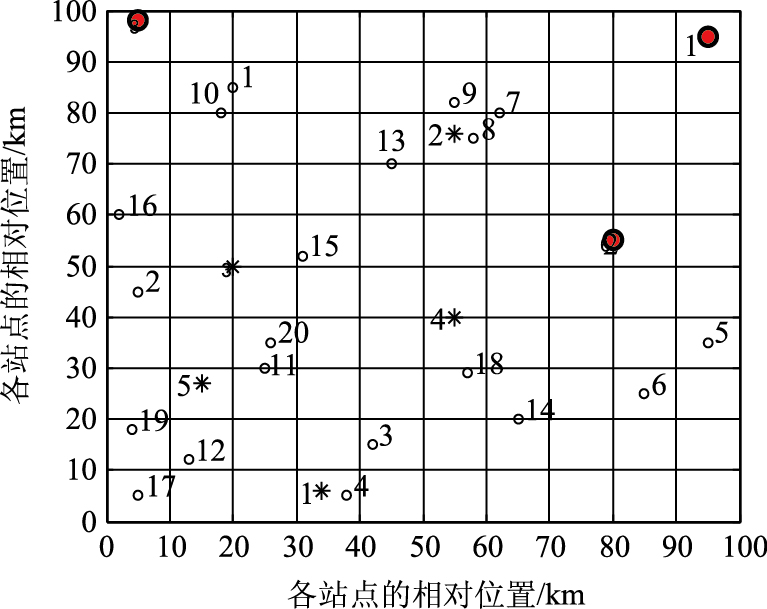
3 算例分析 3.1 数据假设经调研可知,成都市某报废汽车回收拆解公司正面临选址-路径决策。该公司有20家报废汽车回收点,6家中转场候选点,3家拆解中心候选点,其位置如图 2所示。
|
| 注:实心圆圈表示拆解中心候选点;“米”形表示中转场候选点;空心圆圈表示回收点。 图 2 回收站点、中转场和拆解中心的位置图 Fig. 2 Locations of recycling sites,transit depots and disassembly centers |
假定在收集报废汽车过程中,单位运费一致,且假设所有路段的运输条件均相同,即报废汽车运价函数相同。利用网络Google地图测距,得到回收点与候选中转场及拆解中心之间的距离(lz表示回收点到中转场的距离;lc表示回收点到拆解中心的距离)如表 1所示,各中转场候选点至拆解中心候选点距离如表 2所示。
| 回收点编号 | l z/km | l c/km | 回收量/ (veh·d -1) | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 1 | 2 | 3 | ||
| 1 | 43.5 | 60.3 | 71.5 | 76.4 | 80.6 | 45.4 | 22.1 | 38.9 | 24.9 | 3 |
| 2 | 40.7 | 70.2 | 80.1 | 40.7 | 94.9 | 58.1 | 12.5 | 41.3 | 42.4 | 2 |
| 3 | 24.6 | 69.2 | 52.7 | 24.6 | 16.9 | 94.9 | 15.3 | 64.3 | 39.1 | 1 |
| 4 | 29.9 | 80.6 | 68.4 | 43.5 | 35.5 | 100 | 11.6 | 59.2 | 24.9 | 1 |
| 5 | 91.2 | 94.9 | 43.9 | 26.3 | 19.9 | 59.9 | 62.4 | 66.1 | 108 | 2 |
| 6 | 99.3 | 16.9 | 73.5 | 21.7 | 16.9 | 45.4 | 77.9 | 24.9 | 34.6 | 3 |
| 7 | 57.4 | 35.5 | 51.8 | 86.4 | 30.9 | 21.7 | 36.0 | 42.4 | 22.1 | 1 |
| 8 | 68.3 | 19.9 | 18.4 | 47.7 | 21.7 | 86.4 | 62.5 | 39.1 | 12.5 | 1 |
| 9 | 38.9 | 16.9 | 36.9 | 17.3 | 46.4 | 47.7 | 25.4 | 24.9 | 15.3 | 1 |
| 10 | 115 | 106 | 27.1 | 7.1 | 20.7 | 17.3 | 95.4 | 108 | 11.6 | 3 |
| 11 | 30.9 | 8.7 | 9.4 | 28.5 | 37.5 | 7.1 | 1.0 | 34.6 | 62.4 | 2 |
| 12 | 21.7 | 24.3 | 111.3 | 10.7 | 68.4 | 28.5 | 17.8 | 35.5 | 77.9 | 3 |
| 13 | 46.4 | 112 | 20.7 | 90.2 | 43.9 | 10.7 | 27.5 | 19.9 | 36.0 | 1 |
| 14 | 20.7 | 34.6 | 26.1 | 64.3 | 73.5 | 90.2 | 18.5 | 16.9 | 22.1 | 3 |
| 15 | 37.5 | 76.9 | 37.1 | 36.8 | 51.8 | 64.3 | 24.5 | 30.9 | 117 | 2 |
| 16 | 45.4 | 13 | 13.4 | 21.4 | 68.4 | 17.3 | 15.1 | 36.0 | 22.1 | 2 |
| 17 | 58.1 | 67.4 | 118 | 11.3 | 43.9 | 7.1 | 47.5 | 62.5 | 12.5 | 1 |
| 18 | 94.9 | 55.1 | 74.0 | 73.1 | 73.5 | 28.5 | 66.0 | 25.4 | 15.3 | 2 |
| 19 | 100 | 98.3 | 22.5 | 68.9 | 51.8 | 10.7 | 78.7 | 95.4 | 11.6 | 1 |
| 20 | 59.9 | 45.2 | 57.8 | 45.3 | 18.4 | 90.2 | 39.2 | 1.0 | 62.4 | 1 |
| 拆解中心 | 中转场 | |||||
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | 107.9 | 44.3 | 87.5 | 68.0 | 105.0 | 42.7 |
| 2 | 67.2 | 32.6 | 60.2 | 29.2 | 70.8 | 0 |
| 3 | 93.6 | 53.5 | 47.4 | 74.3 | 68.7 | 85.0 |
从回收点到中转场、回收站点到拆解中心以及回收点到拆解中心均采用整车运输,根据对2006年以来的公路货物运输价格指数的分析,结合汽车的平均质量,从回收点到中转场和拆解中心每辆车每千米的运价为0.000 3元/(kg·km),即0.3元/(t·km),中转场到处理中心单位车辆单位里程的运价为0.000 35元/(kg·km),即0.35元/(t·km)。
X公司中转场是基于已有站点的改造扩建,中转场1,2,3,4,5,6的固定建设成本分别为9,10,7,13,12,10。资源整合背景下成立的X公司,其拆解中心采用两条机械拆解线,其专业化和机械化程度较高,拆解中心1,2,3的建设成本分别为500,600,1 000。中转场和拆解中心的建设投资回收期均为15 a。各中转场最大回收能力与最小回收能力、拆解中心最大处理能力与最小处理能力的值如表 3和表 4所示。
| 中转场 | 1 | 2 | 3 | 4 | 5 | 6 |
| 最大回收能力 | 7 000 | 6 000 | 3 700 | 5 400 | 5 800 | 7 600 |
| 最小回收能力 | 600 | 600 | 300 | 610 | 640 | 720 |
| 拆解中心 | 1 | 2 | 3 |
| 最大回收能力 | 7 000 | 8 000 | 9 200 |
| 最小回收能力 | 900 | 600 | 750 |
此外,收集车辆的最大车容量为4辆,运输车辆的最大车容量为12辆。
3.2 模型求解参数设置如下:
(1)遗传算法初始种群规模num=80;最大迭代次数maxgen=500;交叉概率Pc=0.3;变异概率Pm=0.1。
(2)禁忌搜索算法禁忌长度L=10;最大迭代次数stopL=90。
(3)规定遗传搜索过程中gen%N=0(其中N=200),执行禁忌搜索。
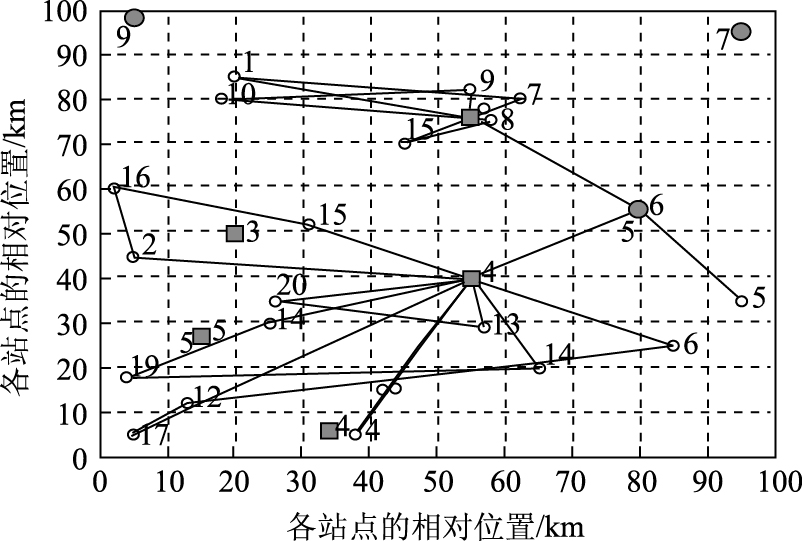
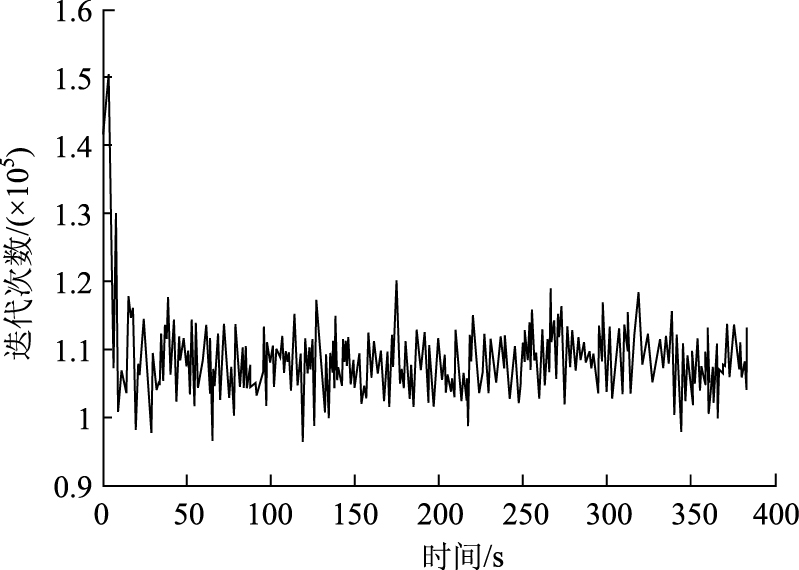
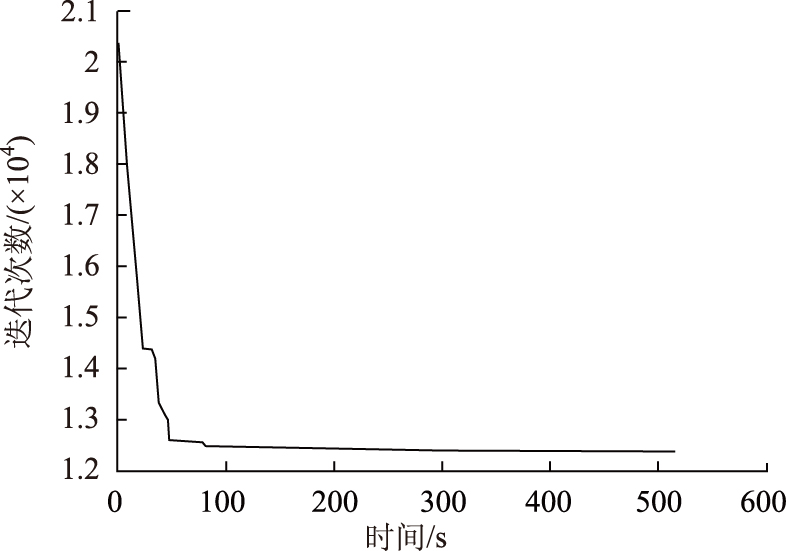
采用仿真计算,使用MATLAB7.9编程实现。最终报废汽车回收网络选址-路径如图 3所示,搜索过程中平均迭代次数变化趋势如图 4所示,搜索过程中最优解迭代次数的变化趋势如图 5所示。
|
| 注: 实心圆圈表示拆解中心;正方形表示中转场;空心圆圈表示回收点。 图 3 废旧汽车回收物流网络选址-选线 Fig. 3 Location-routing inELVs recycling logistics network |
|
| 图 4 平均迭代次数变化趋势图 Fig. 4 Changing trend of average iteration number |
|
| 图 5 最优解迭代次数变化趋势 Fig. 5 Changing trend ofiteration number of optimal solution |
故搜索最终得到的最优解如表 5~表 7所示。
| 选定的拆解中心 | 拆解中心所服务的 中转场 | 拆解中心所服务的 回收站点 |
| 2 | 2,4 | 5 |
| 选定的中转场 | 中转场所服务的回收点 | 中转场所对应的拆解中心 |
| 2 | 1,7,8,9,10,13 | 2 |
| 4 | 2,3,4,6,11,12,14, 15,16,17,18,19,20 | 2 |
| 车辆编号 | 1 | 2 | 3 |
| 对应线路 | 4→15→16→2→4→8 | 2→13→8→2→8 | 8→5→8 |
| 车辆编号 | 4 | 5 | 6 |
| 对应线路 | 2→1→7→2→8 | 4→4→3→4→8 | 2→10→9→2 |
| 车辆编号 | 7 | 8 | 9 |
| 对应线路 | 4→17→12→6→4→8 | 4→14→19→11→4→8 | 4→20→18→4→8 |
我国即将进入报废汽车数量激增的时期,高效率、高效益的回收物流体系是报废汽车回收利用的重要基础,而报废汽车回收物流节点的布局及回收线路的安排在整个回收物流体系构建中又起着举足轻重的作用。本文构建了报废汽车回收物流网络选址-路径优化模型,针对该模型设计了遗传搜索和禁忌搜索组合算法,并以成都某公司为例,采用matlab7.9编程,对模型进行了实例验证。该研究以期能为企业进行报废汽车回收网络设施选址及车辆路径安排提供决策依据,从而实现企业资源利用效率的最大化,并提高报废汽车的回收利用率。文章在各回收点回收量已知的基础上构建模型,将来可以将回收量的不确定性纳入研究范畴,还可进行回收质量、回收时间等的不确定性研究。
| [1] | 赵佳虹,彭艳梅.危险废物回收物流的选址-路径多目标模型[J].交通运输工程与信息学报,2011,9(2):25-29. ZHAO Jia-hong, PENG Yan-mei. A New Multi-objective Model for the Combined Location-routing Problem in Hazardous Waste Recycling Logistics[J]. Journal of Transportation Engineering and Information, 2011,9(2):25-29. |
| [2] | 闻轶. 随机物流选址和车辆径路问题综合优化的研究[D].北京:北京交通大学,2006. WEN Yi. Research on Optimization of Stochastic Location-routing Problem[D].Beijing:Beijing Jiaotong University, 2006. |
| [3] | 张长星,党延忠.定位-运输路线安排问题的遗传算法研究[J].计算机工程与应用,2004,8(3):65-67. ZHANG Chang-xing, DANG Yan-zhong. A Novel Genetic Algorithm for Location-routing Problem[J]. Computer Engineering and Applications, 2004,8(3):65-67. |
| [4] | 曾庆成,杨忠振,蒋永雷.配送中心选址与车辆路径一体优化模型与算法[J].武汉理工大学学报:交通科学与工程版,2009,33(2):267-270. ZENG Qing-cheng, YANG Zhong-zhen, JIANG Yong-lei. Optimization Model and Algorithm of Coordinated Distribution Center Location and Vehicle Routing[J]. Journal of Wuhan University of Technology:Transportation Science & Engineering Edition,2009,33(2):267-270. |
| [5] | 张潜,高立群,胡祥培.集成化物流中的定位-运输路线安排问题(LRP)优化算法评述[J].东北大学学报:自然科学版,2003,24(l):31-34. ZHANG Qian, GAO Li-qun, HU Xiang-pei. Review on Optimal Algorithms of Location-routing Problem(LRP) in Integrated Logistics[J]. Journal of Northeastern University:Natural Science Edition,2003,24(1):31-34. |
| [6] | 汪寿阳,赵秋红,夏国平.集成物流管理系统中的定位-运输路线安排问题的研究[J].管理科学学报,2000,3(2):69-75. WANG Shou-yang, ZHAO Qiu-hong, XIA Guo-ping. Research on Combined Location-routing Problems in Integrated Logistics Systems[J]. Journal of Management Sciences in China,2000,3(2):69-75. |
| [7] | 孙颖荪.汽车回收处理中心的一种选址模型[D].合肥:中国科技大学,2009. SUN Ying-sun. A Location Model for Automobile's Recovery Treatment Center[D]. Hefei:University of Science and Technology of China,2009. |
| [8] | 刘鹤,解棍.基于循环经济理论的汽车逆向物流分析[J].物流技术,2009,28(1):42-43,59. LIU He, XIE Gun. Analysis on the Automobile Reverse Logistics Based on Circular Economy Theory[J].Logistics Technology,2009,28(1):42-43,59. |
| [9] | 李晓玲.报废汽车逆向物流网络构建[D].北京:北京交通大学,2011. LI Xiao-ling. Construction of Reverse Logistics Network of End-of-life Automobile[D]. Beijing:Beijing Jiaotong University,2011. |
| [10] | CHAN Y, CARTER W B, BURNES M D. A Multiple-depot, Multiple-vehicle, Location Routing Problem with Stochastically Processed Demands[J]. |
| [11] | 王勇,张永,毛海军,等.基于改进蚁群算法的多物流中转站选址规划[J].公路交通科技,2011,28(8):140-146. WANG Yong, ZHANG Yong, MAO Hai-jun, et al. Multi-logistics Transfer Stations Allocation Based on Improved Ant Colony Optimization Algorithm[J]. Journal of Highway and Transportation Research and Development,2011,28(8):140-146. |
| [12] | 税文兵,叶怀珍,张诗波.考虑库存成本的配送中心动态选址模型及算法[J].公路交通科技,2010,27(4):149-154. SHUI Wen-bing, YE Huai-zhen, ZHANG Shi-bo. A Dynamic Distribution Center Location Model and Algorithm with Inventory Cost[J]. Journal of Highway and Transportation Research and Development,2010,27(4):149-154. |
 2016, Vol. 33
2016, Vol. 33
