扩展功能
文章信息
- 冯雪, 王喜富
- FENG Xue, WANG Xi-fu
- 考虑自行车流特性的机非混合交通流元胞自动机仿真
- Simulation of Mixed Traffic Flow by Cellular Automaton Considering Bicycle Flow Characteristics
- 公路交通科技, 2016, Vol. 33 (3): 132-137
- Journal of Highway and Transportation Research and Denelopment, 2016, Vol. 33 (3): 132-137
- 10.3969/j.issn.1002-0268.2016.03.022
-
文章历史
- 收稿日期: 2015-06-10
在我国城市支路,机非分隔线作为机动车道与自行车道的划分方式被广泛采用。然而由于自行车道通行能力的限制以及对交通安全性缺乏认识,部分自行车经常穿越机非分隔线行驶在机动车道上,而越行行为引起的机非混行造就了许多不同于匀质交通流的交通特性。因此,深入探讨自行车越线行驶对动态交通流的影响,掌握该影响的作用原理、范围以及程度,将为机动车与自行车道的规划、设计与管理提供理论依据。
近年来,作为自行车的替代出行方式,电动自行车以其更快的运行速度被越来越多的人接受与采用,我国城市的自行车流基本上是以混合自行车流形式出现的。因此,探讨电动自行车比例对越线行驶的自行车数量以及机动车交通流的影响具有重要意义。另一方面,自行车建模过程中通常设定传统自行车与电动自行车的最大速度分别为4 m/s和6 m/s,即实测数据的平均最大速度。而在实际交通环境中,因车辆的结构、性能、使用年限等特性,以及骑行者的年龄、性别、驾驶风格等人为因素,自行车的最大行驶速度具有明显差异性。在已有参考文献中,自行车最大速度的多样性对机动车交通流的影响鲜少提及。
目前,基于元胞自动机的机非混合交通流微观模型的研究较为广泛[1, 2, 3, 4, 5],而充分考虑自行车流特性的微观模型有限。已有的机非混合交通流元胞自动机建模方法主要分为两类:一是以NaSch模型模拟机动车流,并将道路空间进行虚拟子车道的划分,进而借用机动车的多车道元胞自动机模型,并调整相关参数以模拟自行车流[6]。该类方法基本未阐述自行车容易发生侧摆等不同于机动车流的行为特点。为弥补上述缺陷,考虑到自行车骑行时并没有严格的车道概念及跟车行为不典型等原因,Zhao等[7]模糊了自行车换道规则,提出了以NaSch模型模拟机动车流,多值元胞自动机模型[8,9]模拟自行车流的机非混合交通流建模框架,并采用该模型实现了对公交车进出站形成的机非混合交通流的建模与分析。Xie[10],贾宁等[11, 12]进而依据上述建模方法实现了对机非流量、系统输运量随车流密度的变化以及自行车对机动车的干扰模式等研究。尽管多值元胞自动机模型具有建模规则简单,模拟容易实现等优势,然而该类模型对机非干扰的刻画皆基于自行车尽量靠右行驶,与机动车道保持尽可能远距离的假设。该假设在部分交通场景具有局限性,通常适用于特殊路段(如公交车进出站)以及特殊道路结构(如机非共用车道)的建模。
因此在机非分隔线划分车道的场景下,针对上述两类模型的不足,本文在第一类模型的基础上,对机动车流采用修正的NaSch模型,自行车流则结合异质性和最大速度多样性等特性,并引入随机偏移率来表现自行车不遵循车道行驶的行为特点。并辅助数值模拟,以实现自行车行为特点对机动车交通流影响的分析与探讨。
1 模 型本文设定的机非混合交通系统由一条4 m宽的机动车道与一条3 m宽的同向自行车道构成,如图 1所示。考虑到机动车与自行车的车辆占用空间及加速度等参数的差异性,设置元胞的长度与宽度为1 m,进而将机动车道和自行车道划分为并列的4条与3条子车道。自行车占用2×1个元胞,机动车长度7个元胞,考虑到机动车受到自行车的摩擦干扰,机动车宽度依据文献[13]的动态宽度概念进行调整,具体方法如1.2节所述。

|
| 图 1 设置机非分隔线的混合交通系统示意图 Fig. 1 Schematic diagram of mixed traffic system with separated line |
为获取真实速度数据以校正元胞自动机模型,课题组于2014年9月20日至28日期间,在北京市车公庄大街与平安里大街的独立自行车道上对自行车的速度信息进行采集。具体计算瞬时速度的方法如图 2所示。选取l=5 m 的路段,分别记录自行车样本进入及骑出该路段的时刻t1与t2,则自行车的瞬时速度为V=l/(t2-t1)。

|
| 图 2 自行车瞬时速度测量方法 Fig. 2 Method for measuring bicycle instant velocity |
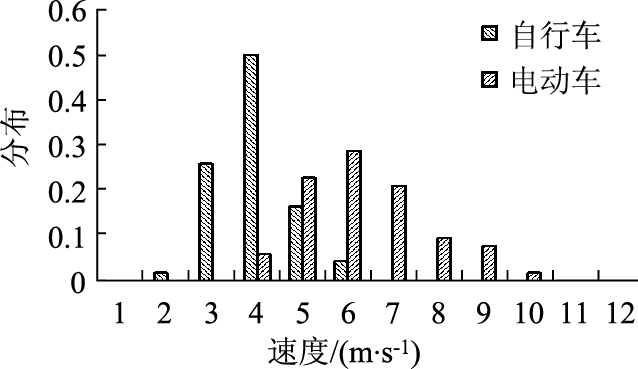
考虑到自行车的车速会不同程度地受到前向与后向自行车的影响,数据采集过程中,筛选不存在过近的前向与后向车辆(车头间距大于10 m)的样本进行记录。最终通过数据采集,分别得到300个自行车与300个电动自行车的样本点,其瞬时速度分布如图 3所示。

|
| 图 3 基于数据采集的传统自行车及电动自行车的瞬时速度分布 Fig. 3 Distribution of data of instant velocities of both conventional bicycles and electric bicycle |
不失一般性,假设基于数据采集的瞬时速度分布可代表自行车随机慢化后的自由速度分布,即任意样本点的瞬时速度代表其自由速度的均值va。设定慢化概率pdec=0.2,则其最大速度可由公式vmax=va+pdec反推产生,因此pdec=0.2时的自行车最大速度分布如图 4所示。
|
| 图 4 pdec=0.2时传统自行车及电动自行车的最大速度分布 Fig. 4 Maximum velocity distribution of both conventional bicycles and electric bicycles when pdec=0.2 |
(1)基本换道规则
如果前方车辆阻碍了自行车j的运行,自行车倾向于为获得更好的骑行条件而变换子车道。自行车子车道变换的前提为:
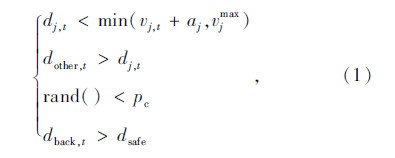
(2)侧向摆动的换道规则
如果自行车在当前子车道与相邻子车道都具有充足的前向距离与安全保证,出于自行车无法直线骑行的运动特点,车辆将按照随机偏移概率pl确定运动方向[14]。自行车侧向摆动的换道规则如下:
如果:

其中pj与pother分别为自行车j选择当前车道以及相邻子车道的概率,N为归一化参数,以保证pj+pother=1。
(3)越线自行车为后方机动车让行规则
当越线行驶的自行车阻碍了后方机动车,则将以一定的概率积极返回自行车道。因此越线自行车j让行规则如下:
如果
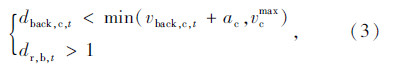
当自行车j完成换道,其纵向运行状态将依据NaSch模型的演化规则进行更新,具体更新规则为:
(1)加速:vj,t+1=min(vj,t+aj,vjmax);
(2)减速:vj,t+1=min(vj,t+1,dj);
(3)随机减速:以概率pdec,vj,t+1=max(vj,t+1-aj,0);
(4)位置更新:xj,t+1=xj,t+vj,t+1。
1.2 机动车子模型已有的机非混合交通流元胞自动机仿真通常只考虑自行车的阻滞行为对机动车的干扰[1, 2],摩擦干扰作为机动车考虑侧向自行车安全而采取的减速行为则较少涉及[14]。Luo等[13]基于由实测数据拟合得到的机动车行车宽度与通过速度的相关关系,提出了一种采用动态机动车行车宽度的修正NaSch模型模拟机动车的行为,并取得了良好的仿真效果。因此,本文借鉴文献[13]的处理方法,制定如下规则以体现自行车对机动车i的干扰:
(1)加速:vi,t+1=min(vi,t+ac,vcmax)。
(2)速度修正:
基于拟合得到的有效路径宽度与车速之间的线性相关关系w+α+β·vi,t=wi,t(其中,w,wi,t分别为机动车物理宽度及有效路径宽度,α与β为拟合参数,分别等于0.309 9,0.131 7),依次计算机动车i前的第k个元胞处(0<k≤vi,t+1)的路径宽度wi,t(k),如果vi,t+1满足w+α+β·vi,t+1>wi,t(k),即当前速度过大,因此,vi,t+1=max{k-1,「[wi,t(k)-w-α]/β },「x
},「x 为小于x的最大整数。
为小于x的最大整数。
(3)随机减速:以概率pcdec,vi,t+1=max(vi,t+1-ac,0)。
(4)位置更新: xi,t+1=xi,t+vi,t+1。
2 数值模拟和分析数值模拟采用周期性边界条件。设定路段长度L=1 000。假设ac=3 m/s2,vcmax=20 m/s,w=1.8 m,pc=0.9,pl=0.2,pg=0.1。初始时刻,机动车与自行车随机分布在机动车与自行车道上,自行车的最大速度依据图 3所示的最大速度分布随机取得。系统每次模拟迭代25 000个时间步。为避免暂态的影响,舍弃前10 000个时间步的数据,模拟结果为后15 000个时间步的平均。
2.1 自行车最大速度多样性对机动车交通流的影响本文首先对考虑最大速度多样性(场景1)和不考虑该多样性(场景2,即设定自行车最大速度为4 m/s,电动自行车最大速度为6 m/s)两种场景下的机动车交通流特性进行对比分析。通过仿真试验得到以Re=0为例,基于不同场景的Nj-ρc以及qc-ρc相关关系曲线,分别如图 5、图 6所示,其中空心符号与实心符号分别表示场景1与场景2中所讨论指标的变化趋势。

|
| 图 5 Re=0条件下,考虑最大速度多样性与不考虑多样性的qc变化规律的比较图 Fig. 5 Comparison of qc variation between scenarios with and without maximum velocity variation when Re=0 |

|
| 图 6 Re=0条件下,考虑最大速度多样性与不考虑与不考虑多样性的Nj变化规律的比较图 Fig. 6 Comparison of Nj variation between scenarios with and without maximum velocity variation when Re=0 |
可以看出,相同机动车密度条件下,两种场景下的机动车的流量皆随自行车密度的增加而降低,且场景1的机动车流量分布、自行车越线行驶数量与场景2的基本一致。该现象可做如下解释:尽管自行车最大速度的多样性增大了速度差及快车试图超越慢车的频率,当自行车道密度相对较低时,自行车具有较充足的行驶空间,场景1中的快车能够通过变换子车道及时超越慢车,因此,越线行驶自行车数量及对机动车交通流的影响不明显。当自行车密度较高时,自行车普遍受到前车的影响从而无法自由行驶,平均车速相对较低,最大速度的多样性对自行车流基本无影响,进而对越线数量及机动车流的影响有限。因此,数值模拟结果表明,在进行机非混合交通流元胞自动机的建模与仿真过程中,可采用每类自行车最大速度的均值代替实测交通流中最大速度的多样性。
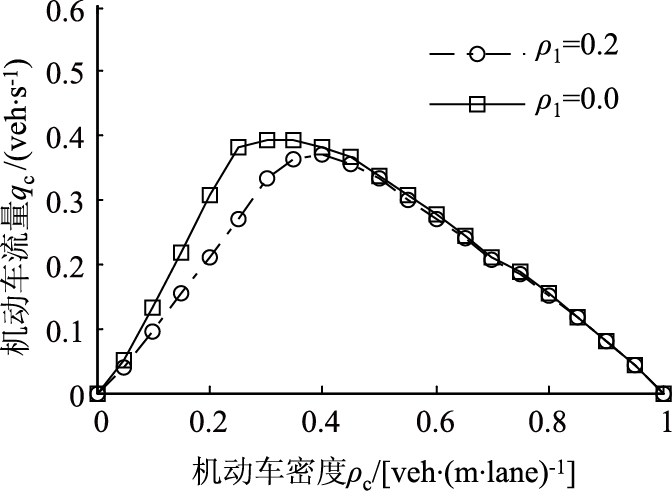
2.2 自行车侧向摆动特性对机动车交通流的影响通过数值模拟,进一步对考虑自行车侧向摆动行为(场景3)和无侧向摆动(场景4)两种场景下的机动车交通流特性进行对比分析。图 7、图 8分别为ρb=0.1,Re=0条件下,基于上述两种场景的qc-ρc,Nj-ρc相关关系的比较图。
|
| 图 7 ρb=0.1、Re=0条件下,考虑自行车侧向摆动行为与无侧向摆动的qc变化规律的比较图 Fig. 7 Comparison of qc variation between scenarios with and without drifting when ρb=0.1 and Re=0 |

|
| 图 8 ρb=0.1、Re=0条件下,考虑侧向摆动行为与无侧向摆动的Nj变化规律的比较图 Fig. 8 Comparison of Nj variation between scenarios with and without drifting when ρb=0.1 and Re=0 |
可以看出,考虑侧向摆动的机动车流量及自行车越线行驶数量分布与无侧向摆动场景存在较大差异:由于自行车的侧向摆动容易干扰后方自行车的前行,进而增大换道率,模拟结果显示在任意机动车密度条件下,侧向摆动的发生对自行车越线数量皆有提升作用。而当机动车流密度较低时,车辆间平均距离较大,机动车之间几乎不存在相互作用,主要受到来自自行车的干扰。因此,场景3中的自行车越线行驶数量增大同时伴随机动车流量的降低。而机动车高密度状态下,机动车行驶将受前车距离的影响。随着机动车车辆间距的减小,自行车如果产生借用车道超车的意愿,出于对交通安全方面的考虑,插入机动车间隙进而干扰机动车的运行的行为基本不会发生,此时机动车的行为与自行车基本无关,因此两种场景下的曲线没有明显差异。综上所述,仿真结果显示,不考虑自行车的侧向摆动将过低估计自行车越线行驶数量、机非干扰的危险性以及机动车中低密度下的机动车流量。因此,自行车的侧向摆动行为应纳入机非混合交通流建模过程中。
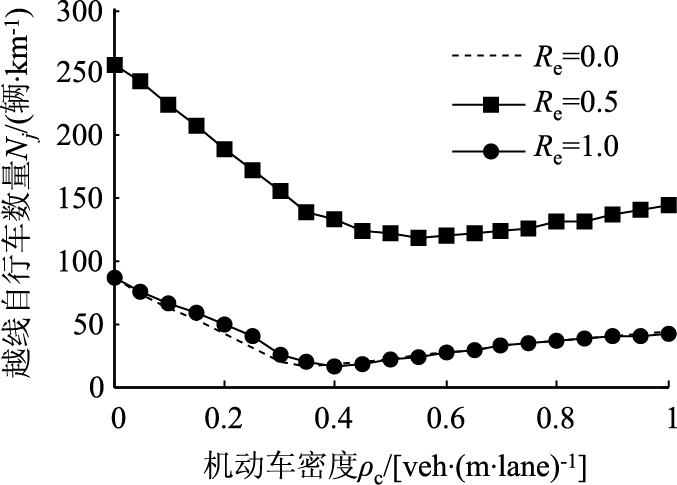
2.3 电动自行车比率对机动车交通流的影响为探讨电动自行车比例对机动车交通流的影响,图 9、图 10分别显示了ρb=0.1条件下,机动车流量和越线行驶自行车数量随机动车密度及电动自行车比例的变化规律。由图 9、图 10首先可以看出,在机动车中低密度条件下,电动自行车流(Re=1)比传统自行车流(Re=0)更易引起自行车越线的发生及机动车流量的下降。该现象可解释为电动自行车具有更快的行车速度及更高的前向距离的需求,因此更易受前车干扰从而发生越行。而与纯自行车流(Re=0)和纯电动自行车流(Re=1)相比较,混合自行车流(0<Re<1)将增大速度的差异性,自行车道上的传统自行车容易形成“塞子”阻碍电动自行车的超车行为,迫使电动自行车更易换道至机动车道。因此,如图 9、图 10所示,混合自行车流在机动车中低密度条件下具有更高的越出自行车数量和更低的机动车流量。而在机动车高密度范围内,尽管混合自行车越线数量始终高于同质自行车流,机动车流的差异性则逐渐消失。如2.2节所述,机动车与自行车间的相互干扰性降低,因此自行车异质性对机动车流的影响较为有限。

|
| 图 9 ρb=0.1条件下,qc随ρc和Re的变化关系 Fig. 9 The variation of qc with ρc and Re for ρb=0.1 |
|
| 图 10 ρb=0.1条件下,Nj随ρc和Re的变化关系 Fig. 10 The variation of Nj with ρc and Re for ρb=0.1 |
机非混合交通流是我国城市长期存在的交通模式,对其进行建模与仿真分析具有较强的理论与现实意义。本文在NaSch模型的基础上,结合自行车交通流的几类典型特性,建立了城市支路混合交通流元胞自动机模型。而通过数值模拟与分析发现,自行车最大速度多样性对机动车交通流基本无影响,因此在混合交通流仿真过程中可采用每类自行车的最大速度的平均值进行替代。而传统自行车与电动自行车的混行、自行车的侧向摆动特性均是增加自行车相互干扰、诱发自行车越线行驶进而干扰机动车运行的重要因素。因此为更加真实地反映道路上机非混合交通流的关键特性,应在元胞自动机建模与模拟过程中,给定车道宽度和非机动车道宽度、机非流量和不同电动车混合率等条件下,充分考虑上述自行车流的典型特性,从而为城市道路设计规范相关参数取值提供借鉴和参考。
| [1] | ZHAO Xiao-mei, JIA Bin, GAO Zi-you.Traffic Interactions between Motorized Vehicles and Non- motorized Vehicles Near a Bus Stop[J]. |
| [2] | JIANG Rui, JIA Bin, WU Qing-song.Stochastic Multi-value Cellular Automata Models for Bicycle Flow[J]. |
| [3] | 李新刚,高自友,赵小梅,等.混合非机动车流的多值元胞机模型模拟研究[J].物理学报,2008, 57(8):4777-4785. LI Xin-gang,GAO Zi-you,ZHAO Xiao-mei,et al.Multi-value Cellular Automata Model for Mixed Non-motorized Traffic Flow[J].Acta Physica Sinica,2008,57(8):4777-4785. |
| [4] | XIE Dong-fan, GAO Zi-you, ZHAO Xiao-mei.Combined Cellular Automaton Model for Mixed Traffic Flow with Non-motorized Vehicles[J]. |
| [5] | GUO Hong-wei, GAO Zi-you, ZHAO Xiao-mei, et al.Dynamics of Motorized Vehicle Flow under Mixed Traffic Circumstance[J].Communications in Theoretical Physics, 2011(4):719-724. |
| [6] | 高自友, 李克平,李新刚.基于元胞自动机的交通系统建模与模拟[M].北京:科学出版社,2007. GAO Zi-you, LI Ke-ping, LI Xin-gang.Models and Simulations of Traffic System Based on the Theory of Cellular Automaton[M].Beijing:Science Press, 2007. |
| [7] | 贾宁,马寿峰.考虑摩擦干扰的机非混合交通流元胞自动机仿真[J].系统仿真学报,2011,23(2):390-393. JIA Ning, MA Shou-feng.Simulation of Mixed Traffic Flow with Friction Interference Using Cellular Automata[J]. Journal of System Simulation,2011,23(2):390-393. |
| [8] | 贾宁,马寿峰.自行车干扰下机动车交通流的元胞自动机模型[J].系统工程理论与实践,2010,30(7):1333-1339. JIA Ning, MA Shou-feng.Cellular Automaton Model for the Motor-vehicle Flow under the Interference of Bicycles[J].Systems Engineering- Theory & Practice, 2010, 30(7):1333-1339. |
| [9] | 谢东繁.基于微观模型的城市道路交通流若干典型问题研究[D].北京:北京交通大学,2010. XIE Dong-fan.Analysis of Typical Problems of Urban Road Traffic Flow Based on Microscopic Models[D].Beijing:Beijing Jiaotong University,2010. |
| [10] | 郭宏伟.城市路内停车影响的建模与特性分析[D].北京:北京交通大学,2011. GUO Hong-wei.Modeling and Properties Analyzing of Influence of Urban On-street Parking[D].Beijing:Beijing Jiaotong University,2011. |
| [11] | 李珊珊.平交路口机动车自行车行人及其相互干扰微观行为模型研究[D].北京:北京交通大学,2013. LI Shan-shan.Research on Microscopic Behavior Models of Vehicle, Bicycle, Pedestrian, and Their Interactive Interferences at Signalized Plane Intersection[D]. Beijing:Beijing Jiaotong University, 2013. |
| [12] | HU Xiao-jian, WANG Wei, YANG Hai-fei.Mixed Traffic Flow Model Considering Illegal Lane- changing Behavior:Simulations in the Framework of Kerner's Three-phase Theory[J]. |
| [13] | LUO Yong-ji, JIA Bin, LIU Jun, et al.Modeling the Interactions between Car and Bicycle in Heterogeneous Traffic[J]. |
| [14] | 邓建华.基于元胞自动机的自行车流蛇行、穿插模型[J].武汉理工大学学报:交通科学与工程版, 2011, 35(1):198-200,204. DENG Jian-hua.A Snaking and Interweaving Bicycle Flow Model Based on Cellular Automata[J].Journal of Wuhan University of Technology:Transportation Science & Engineering Edition,2011, 35(1):198-200,204. |
 2016, Vol. 33
2016, Vol. 33
