公路交通科技  2016, Vol. 33 Issue (3): 120-126,145

扩展功能

文章信息

向勇, 罗禹贡, 曹坤, 李克强
XIANG Yong, LUO Yu-gong, CAO Kun, LI Ke-qiang
基于车-车通信的自动换道控制
Automatic Lane Change Control Based on Vehicle-to-vehicle Communications
公路交通科技, 2016, Vol. 33 (3): 120-126,145
Journal of Highway and Transportation Research and Denelopment, 2016, Vol. 33 (3): 120-126,145
10.3969/j.issn.1002-0268.2016.03.020

文章历史

收稿日期: 2015-03-19
引用本文 0
向勇, 罗禹贡, 曹坤, 李克强. 基于车-车通信的自动换道控制[J]. 公路交通科技, 2016, Vol. 33 (3): 120-126,145.
XIANG Yong, LUO Yu-gong, CAO Kun, LI Ke-qiang. Automatic Lane Change Control Based on Vehicle-to-vehicle Communications[J]. Journal of Highway and Transportation Research and Denelopment, 2016, Vol. 33 (3): 120-126,145.
基于车-车通信的自动换道控制
向勇1 , 罗禹贡1,2, 曹坤1, 李克强1    
1. 清华大学 汽车安全与节能国家重点实验室, 北京 100084;
2. 北京电动车辆协同创新中心, 北京 100081
收稿日期: 2015-03-19
基金项目: 国家重点基础研究发展计划(九七三计划)项目(2011CB711204);汽车安全与节能国家重点实验室自主科研项目(ZZ2011-092).
作者简介: 向勇(1989-),男,四川安岳人,硕士研究生.
摘要: 针对现有自动换道控制策略存在未考虑换道过程中周围车辆运动状态变化影响的不足,提出了一种基于车-车通信的自动换道控制策略,主要包括动态换道轨迹规划和滑模轨迹跟踪控制。其中,动态换道轨迹规划方法能够根据车-车通信所提供的实时信息更新参考换道轨迹,使得换道车辆适应周围车辆运动状态变化,通过求解基于换道时间和换道距离的带约束非线性优化问题,实时地获取换道过程中约束条件增加或发生改变情形下的安全参考换道轨迹。滑模轨迹跟踪控制通过车辆实际位姿和期望位姿之间的偏差计算轨迹跟踪所需期望速度和横摆角速度。仿真结果表明:所提出的控制策略能有效解决在换道过程中周围车辆车速变化或车辆切入等情况下的自动换道难题,从而能够实现安全舒适的自动换道过程。
关键词: 汽车工程     自动换道     约束优化     轨迹规划     轨迹跟踪    
Automatic Lane Change Control Based on Vehicle-to-vehicle Communications
XIANG Yong1 , LUO Yu-gong1,2, CAO Kun1, LI Ke-qiang1    
1. State Key Laboratory of Automotive Safety and Energy, Tsinghua University, Beijing 100084, China;
2. Beijing Collaborative Innovation Center of Electric Vehicles, Beijing 100081, China
Abstract: The present automatic lane change maneuvers seldom consider the change of the motion states of the vehicles around the host vehicle during the lane change process. To overcome the shortcoming, an automatic lane change maneuver based on vehicle-to-vehicle communications is proposed. The maneuver includes dynamic trajectory planning and sliding-mode trajectory tracking control. The dynamic trajectory planning method can update the reference trajectory according to the real-time information acquired through vehicle-to-vehicle communications to adapt to the motion variation of the vehicles around. The solution of the constrained non-linearly optimization problem based on lane change time and lane change distance acquires a real-time safety reference lane change trajectory when the constraints increase or change during the lane change process. The sliding-mode trajectory tracking control method calculates the desired velocity and yaw rate based on the position and pose error between the actual and desired states. The simulation result shows that the proposed automatic lane change maneuver can settle the problem caused by acceleration/deceleration or cut-in of other vehicles during lane change to accomplish the lane change task safely and comfortably.
Key words: automobile engineering     automatic lane change     constrained optimization     trajectory planning     trajectory tracking    
0 引言

汽车行驶过程中因车道变换发生的交通事故不占少数，尤其是造成交通事故后涉及到多条车道，带来的交通延误影响更大[1]，因而为提高道路安全性和道路通行效率，有必要对车道变换行为进行研究。此外，通信技术的进步和计算成本的降低使得自动换道的实现成为可能[2]，因而对自动换道的研究越来越受重视。

Chee等[3]在智能化公路系统的自动换道策略研究中提出了虚拟期望换道轨迹的概念，并以换道过程中的梯形横向加速度轮廓设计换道轨迹。该研究中仅考虑了换道车辆自身的运动学和动力学，而未考虑周围车辆对换道的影响。

李玮等[4]在其研究中总结了现有车辆换道轨迹函数的特点，提出了一种基于正弦函数和双曲正切函数的换道轨迹函数，并通过B样条理论对换道轨迹进行再规划。该研究中的换道轨迹虽然综合了正弦函数和双曲正切函数的优点，但是并未从根本上克服现有换道轨迹函数的不足。

Petrov等[5]设计了一种双层非线性自适应转向控制器来实现自动换道，该策略以摆线为期望换道轨迹，通过轨迹跟踪控制实现自动换道，但只考虑了换道车辆前方有一辆静止车辆需要避撞的情形。

国内外基于多项式函数设计的自动换道轨迹满足换道轨迹的各项需求，是一种理想的换道轨迹函数。现有研究中基于多项式轨迹函数的自动换道研究虽然考虑了周围车辆避撞的问题，但只是在换道初始时刻进行了计算，并不能保证整个换道过程的安全[6, 7, 8, 9, 10]。

总的来说，现有自动换道的研究还未考虑换道过程中周围车辆运动状态变化对换道车辆的影响。利用车-车通信技术能在换道过程中很好地识别车辆周围的环境，从而根据周围车辆运动状态的变化制订相应的控制策略。因此本文提出一种基于车-车通信的自动换道控制策略。跟车安全性和道路通行效率之间的相互制约关系对安全跟车时距存在影响，但是车-车通信技术能提高车辆间传递信息的实时性，缩短反应时间，缩短车与车之间的安全跟车时距，从而提高道路通行效率。得益于车-车通信技术，跟车过程中车辆间的安全车间距理论上可以为零。此外，车-车通信提供的实时信息还能及时监测潜在碰撞危险，存在潜在碰撞危险时，重新规划安全的换道轨迹，避免碰撞的发生。该自动换道控制策略通过优化求解得到换道时间和换道距离，在换道初始时刻以及换道过程中不同约束条件下均能得到合理的换道轨迹。采用滑模轨迹跟踪控制器使得换道车辆能够准确地跟上期望的换道轨迹，并且使得稳态误差接近于零。最后通过Matlab/Simulink和CarSim联合仿真平台对本文所提出的自动换道控制策略进行仿真验证。

本研究主要进行自动换道控制策略的理论研究，基于车-车通信和GPS等传感器的信息获取不作本阶段的重点研究对象。

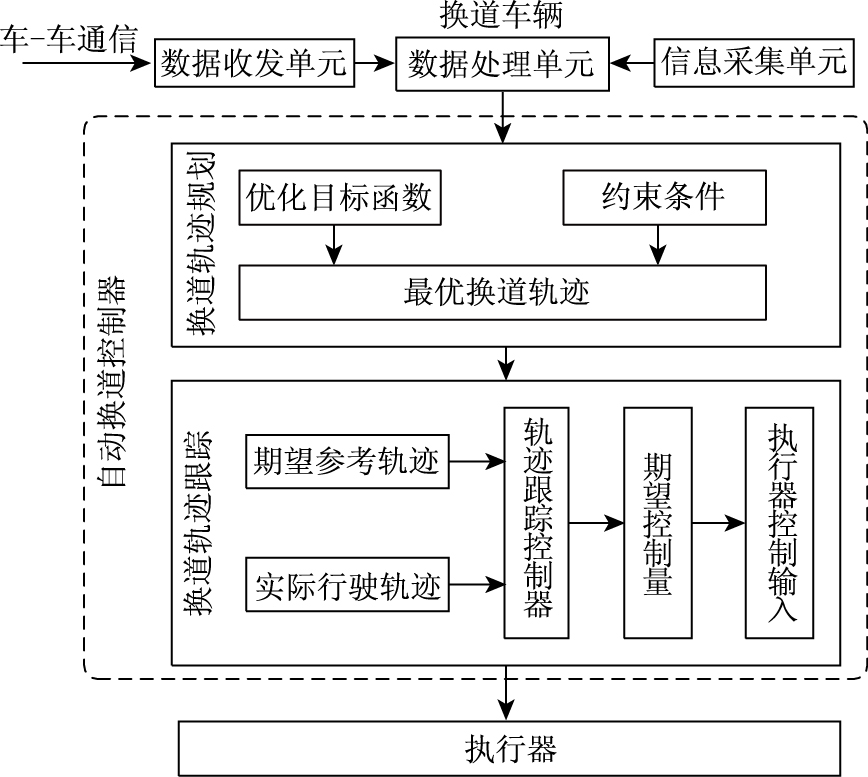
1 动态自动换道控制策略

车辆在车-车通信和自车传感器获得信息的基础上，实现自动换道功能的逻辑如图 1所示。车辆以车-车通信的方式获取周围车辆的位置、速度和加速度等信息。车辆自身信息通过车载传感器获取，如GPS获取位置信息，速度传感器和加速度传感器分别获取速度和加速度信息，摄像头采集到的数据进行图像处理可得到车道宽度等信息。自动换道控制器根据相关信息实时规划一条满足安全性、舒适性和通行效率要求的换道轨迹，然后对其进行轨迹跟踪控制，实现自动换道。

图 1 动态自动换道控制策略 Fig. 1 Dynamic automatic lane change maneuver
图选项
2 自动换道控制器设计 2.1 换道轨迹规划

研究表明，除了加速度，加加速度的变化也是引起乘坐不舒适的重要原因[11]。因而为保证换道过程的舒适性，不仅需要考虑加速度，还要考虑加加速度。另外换道距离影响整个交通流和通行效率，该距离越短，对整个交通流的影响越小，通行效率越高。综合考虑上述因素，本文建立式(1)中以降低加加速度变化和缩短换道距离为目标的代价函数来求取最优换道轨迹。

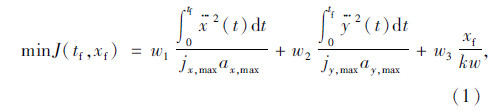
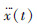式中，tf为换道时间；xf为换道距离；w1，w2和w3为权重系数；为换道轨迹纵向时间函数的三次导数(即纵向加加速度)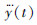；为轨迹函数横向时间函数的三次导数(即横向加加速度)；jx,max为最大纵向加加速度；ax,max为最大纵向加速度；jy,max为最大横向加加速度；ay,max为最大横向加速度；w为车道宽；k为常数。右边第1、第2项分别为纵横向加加速度平方对时间积分后无量纲化的结果，表征加加速度变化；第3项为换道驶过的纵向距离无量纲化的结果。

为实现换道轨迹规划，首先选择理想的轨迹函数形式(即式(2)中的五次多项式函数)作为换道轨迹函数。因为由该函数得到的换道轨迹不仅具有三阶连续可导和曲率连续不突变的优点，还能很好地模拟实际换道轨迹，并将纵横向解耦。

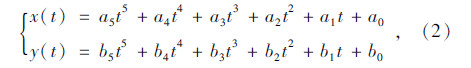
式中,a0～a5，b0～b5为轨迹函数中的未知系数; t为换道开始后的时间。

求解轨迹函数中的未知系数，考虑换道过程的边界条件：换道轨迹起点和换道初始时刻的状态一致，轨迹终点和换道结束时刻期望的状态一致，即式(2)中换道轨迹起点和终点的位置、速度和加速度与对应的实际值或期望值相同，如式(3)和式(4)所示。

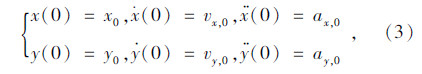
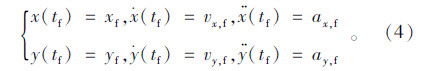
以换道初始时刻的车辆位置为参照建立地面坐标系，即以车辆质心为坐标原点，车辆行驶的方向为x轴，车辆左方为y轴，建立车辆坐标系。0表示换道开始时刻，f表示换道结束时刻。假设车辆沿着车道中心线以原始车道上的平均车速匀速行驶，则x0=y0=0，vx,0=vo。另外假设初始时刻车辆的纵、横向加速度及横向速度均为零，即ax,0=ay,0=0，vy,0=0，以及换道结束后车辆沿着目标车道的车道中心线以该车道上的平均车速做匀速直线运动，则ax,f=ay,f=0，vx,f=vd，vy,f=0。假设各车道宽相同，则换道驶过的横向距离yf为车道宽w。其中v0，vd，w均可从输入换道控制器中的数据得到，但是换道时间tf和换道距离xf却是未知的。

现有研究中大多人为预先给定tf和xf，这样结合式(3)和式(4)中的边界条件就可以将式(2)中轨迹函数的未知系数求解，进而得到换道轨迹函数。但是由其计算过程可知，得到的换道轨迹是建立在给定tf和xf的基础上，而合理的tf和xf需要根据试验数据统计结果来给定。实际上，不同场景下的统计结果存在较大差别，而且为获得准确有效的统计结果需要大量试验数据，这大大降低了其灵活性和实用性。因而本文提出将tf和xf作为待求解的自由变量，依据不同场景下的约束条件进行求解，自动得到适应不同场景的结果，使之能适用于不同场景。这样式(2)中的轨迹函数以及式(3)、式(4)中的边界条件构成了一个包含12个方程和14个未知变量的静不定问题。该问题没有唯一解，不能直接求得解析解。但是式(2)中的未知参数可以据此全部表达为tf和xf的函数，因而轨迹函数(2)也成为tf和xf的函数。

因为自动换道轨迹规划问题不是一个单纯的数学问题，其物理意义决定了它还具有其他约束条件。这包括换道过程中的加速度和加加速度绝对值不能超过阈值，纵向速度不能超过最大值，以及换道过程的安全性由最小安全距离模型来保证[12, 13]。其中，最小安全距离模型是指为避免换道过程中发生碰撞，轨迹规划初始时刻相关车辆间所应该具有的最小纵向距离。该模型建立在对换道过程中车辆的运动学特性分析基础上，具有重要的实际应用意义[14]。

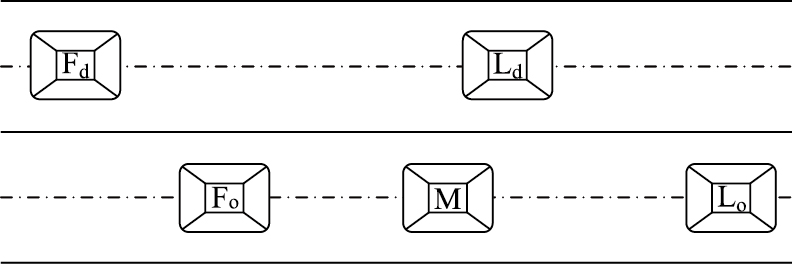
如图 2所示的换道场景中，换道车辆M和目标车道前车Ld、目标车道后车Fd、原始车道前车Lo和原始车道后车Fo之间的最小安全距离MSSLd,M，MSSFd,M，MSSLo,M和MSSFo,M的计算公式分别为[12, 13]：

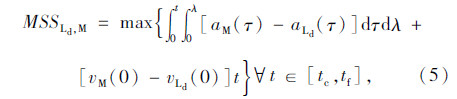
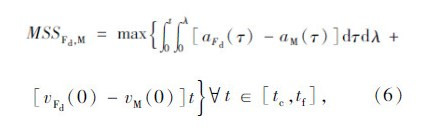
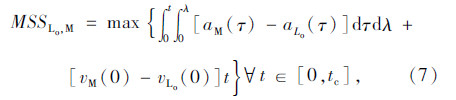
式中，vM，vLd，vFd，vLo，vFo为各车速度；aM，aLd，aFd，aLo，aFo为各车加速度；tc为相应车辆间的临界碰撞时刻；tf为换道结束时刻，τ和λ为积分变量。

图 2 换道场景 Fig. 2 Lane change scenario
图选项

换道过程中存在的约束条件为：

式中，vx,max为纵向速度的阈值；d0为车辆间巡航行驶时所应保持的最小纵向距离；dLd,M，dFd,M，dLo,M和dFo,M分别为M与Ld，Fd，Lo，Fo之间的当前车间距。

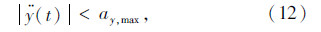
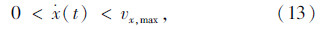
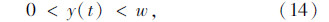
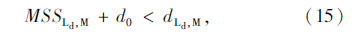
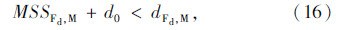
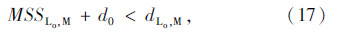
由式(2)～(4)计算可知，式(1)中的加加速度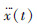和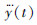是tf和xf的函数。则式(1)中的目标函数和式(9)～(18)中的约束条件描述了换道轨迹规划条件下的以换道时间tf和换道距离xf为自变量的带约束的非线性优化问题。该优化问题能够根据不同环境条件下的约束条件自动求解出优化后的换道时间和换道距离，从而解决不同环境条件下的换道轨迹规划问题,得到的换道轨迹在保证换道安全性和舒适性的同时还保证换道距离最短。

2.2 换道轨迹跟踪

为了实现对上述规划换道轨迹的跟踪，本文以当前车辆位姿和期望位姿之间的偏差为输入，基于滑模控制设计了轨迹跟踪控制器[15, 16]。

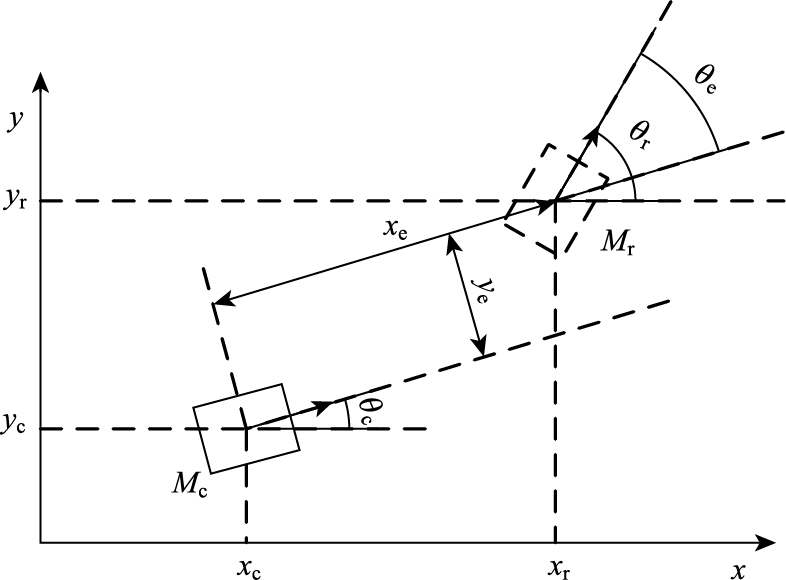
如图 3所示，车辆的位姿由其质心在地面坐标系的位置和其航向角来表示。pc=(xc,yc,θc)T和pr=(xr,yr,θr)T分别为车辆当前实际的纵向位移、横向位移和航向角，对应时刻期望的纵向位移、横向位移和航向角；下标c表示当前时刻的实际状态，下标r表示对应时刻的期望状态。Mc为当前位置的车辆，Mr为期望位置的车辆。令qc=(vc,ωc)T，其中vc和ωc分别为车辆当前实际的速度和横摆角速度，在运动学模型中它们是控制输入。车辆的运动学方程为：

图 3 轨迹跟踪偏差 Fig. 3 Errors of trajectory tracking
图选项

在当前车辆坐标系中，根据坐标变换公式，可得位姿偏差为：

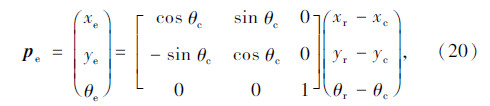
位姿偏差的微分方程为：

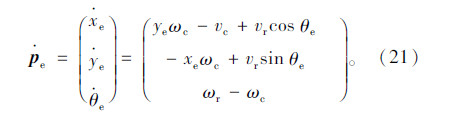
式中，下标c表示当前时刻的实际状态；下标r表示对应时刻的期望状态；下标e表示当前时刻期望状态和实际状态之间的偏差。

车辆的轨迹跟踪控制就是计算控制输入qc=(vc,ωc)T，使得对任意的初始误差，在该控制输入作用下，pe=(xe,ye,θe)T有界，且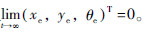

可以证明，只要xe收敛到零且θe收敛到－arctan(vrye)，则ye收敛到零，从而有θe收敛到零[16]。基于反演法设计滑模控制器的切换函数：

为满足达到滑动模态的条件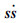<0，选取等速趋近律：

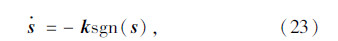
式中，k为常数向量，sgn为符号函数，若x>0，则sgn(x)=1； 若x<0，则sgn(x)=-1； 若x=0，则sgn(x)=0。

在式(22)的滑模控制作用下，系统将于有限时间内达到滑动模态。

为减小滑模控制存在的抖振，采用连续函数(24)取代式(23)中的符号函数：

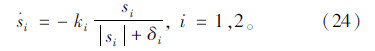
式中，si，ki为向量s，k中的变量；δi为使得式(24)接近式(23)的调节变量。

得到控制律为：

式中，

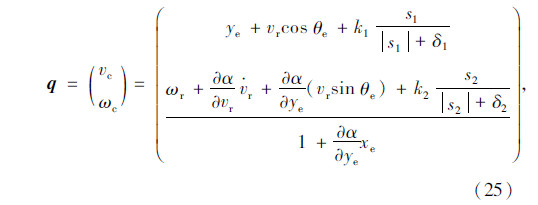
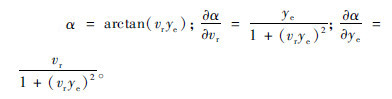3 不同场景下自动换道仿真结果

为验证本文所提出的自动换道控制策略在不同约束条件下的正确性和有效性，设计了如下两种具有代表性的场景。

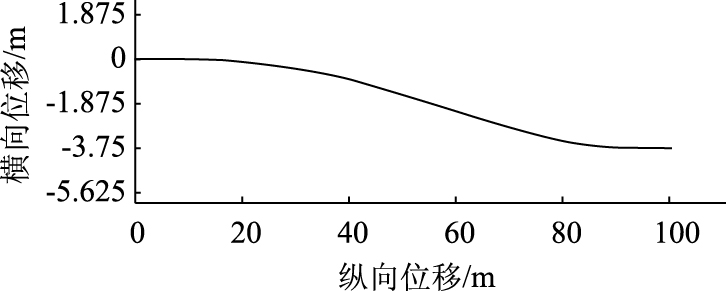
3.1 目标车道平均车速低于原始车道平均车速

当车辆准备驶离高速公路，提前换到出口对应的车道时，通常目标车道上的平均车速低于原始车道上的平均车速。假设目标车道平均车速为vd=14 m/s，原始车道平均车速为vo=20 m/s,M周围没有其他车辆，由式(1)～(4)和式(9)～(14)，以及表 1中参数计算得到图 4中的最优换道轨迹。

表 1 参考轨迹的换道工况1 Tab. 1 Lane change condition 1 of reference trajectory
平均车速/ (m·s -1) 车道 宽/m 最大纵向 车速/ (m·s -1) 最大加速度/ (m·s -2) 最大加加速度/ (m·s -3)
原始车道 目标车道 纵向 横向 纵向 横向
20 14 3.75 20 5 2 2 1
表选项
图 4 最优换道轨迹1 Fig. 4 Optimal lane change trajectory 1
图选项

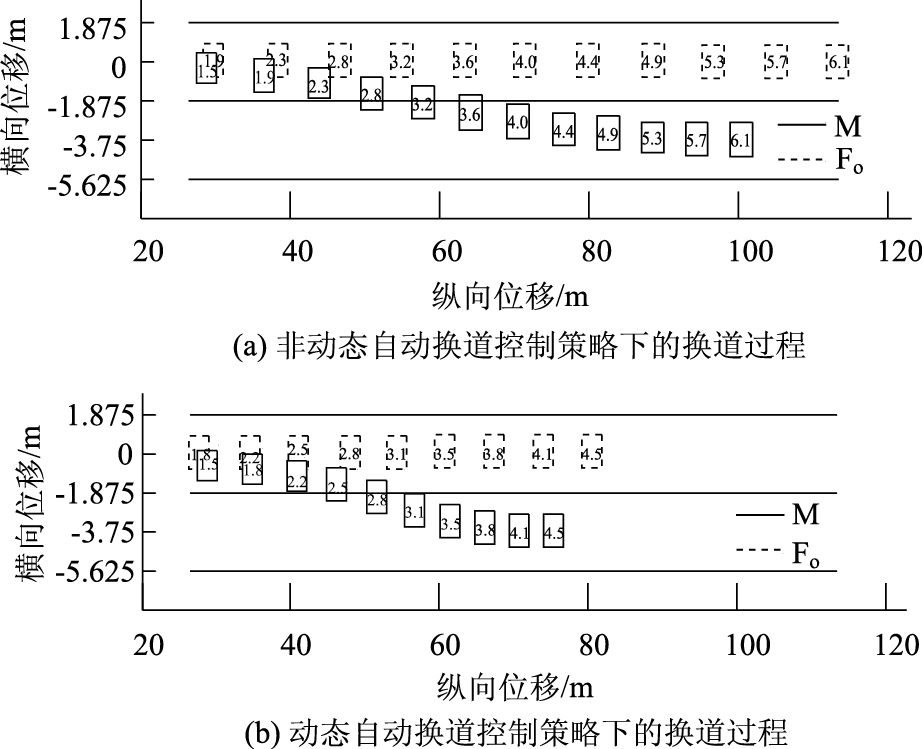
当M沿着该最优轨迹进行换道至1.5 s时，原始车道后面突然出现Fo。此时Fo与M的距离为5 m(得益于车-车通信技术，跟车情形下的安全车间距可以为0 m，因而不考虑换道过程的安全，该情形下是可以进行换道的)，并以vFo=20 m/s的车速匀速行驶。按照M当前的换道轨迹和Fo的运动状态计算出对应的最小安全距离MSSFo,M为3.86 m。由式(15)知道，当M和Fd的车间距小于6.86 m时，沿着原来的轨迹行驶在3 s附近车间距小于3 m，有潜在碰撞危险，如图 5(a)。因而需要对M的换道轨迹进行重新规划。和之前相比，增加了(15)式中的约束条件。以式(1)为目标函数，式(9)～(15)为约束条件，求得新的换道轨迹后的换道过程如图 5(b)所示，车辆之间没有碰撞危险，M能安全地完成换道过程。

注: 图中代表车辆的矩形中的数字是车辆行驶至所在位置的时刻,下同。 图 5 Fo影响下不同换道过程对比 Fig. 5 Comparison of different lane changes under influence of Fo
图选项

和沿着没有Fo的最优换道轨迹换道过程相比，新的换道过程时间更短，换道驶过的纵向距离也更短。由于为了达到目标车道上的车速，整个换道过程中M都在减速,为保持和Fo之间大于d0的车间距，必须增大方向盘转角，尽快到达目标车道。从而缩短了换道时间，换道过程的平均车速也更低。

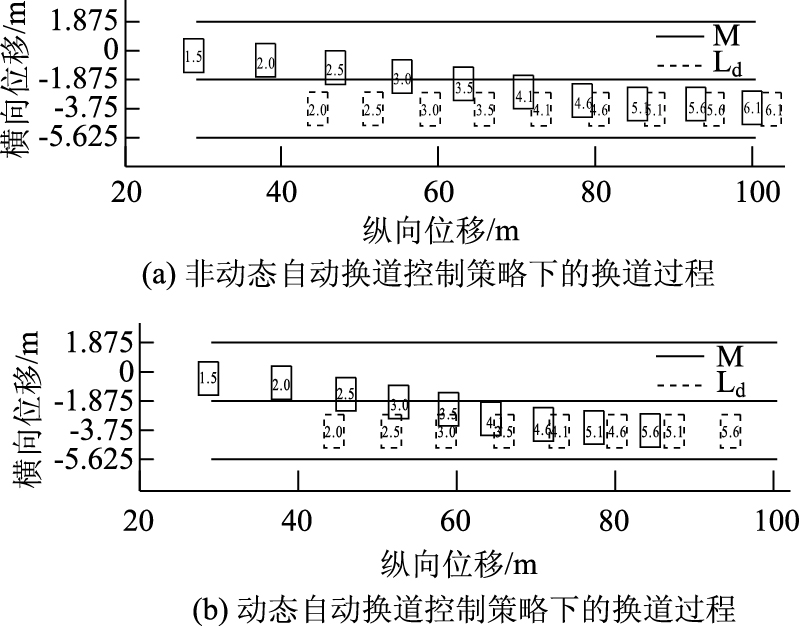
类似地，当M换道进行到1.5 s时，其目标车道前方突然出现Ld，它与M的纵向距离为6 m，并以vLd=14 m/s的车速匀速行驶。由式(5)计算得到的最小安全距离为6.64 m，继续沿着原来的轨迹换道有碰撞危险，因而需根据当前条件重新规划M的换道轨迹。两种情形下的换道过程对比如图 6所示，依据式(1)和式(9)～(15)重新规划后的换道轨迹能避免潜在碰撞。同前面遇到Fo相比，约束条件发生了改变。

图 6 Ld影响下不同换道过程对比 Fig. 6 Comparison of different lane changes under influence of Ld
图选项

为避免碰撞，新的换道过程时间更短，纵向距离也更短。因为新的换道过程中，M必须增大方向盘转角，同时M的车速降低得也较快，与前面遇到Fo相同。

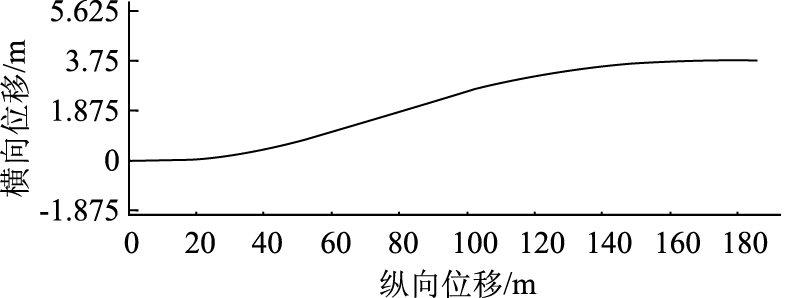
3.2 目标车道平均车速高于原始车道平均车速

当前方车辆车速低于期望行驶车速或车辆准备超车时，车辆通常换到左边车速较高的车道上。假设目标车道平均车速为vd=30 m/s，原始车道平均车速为vo=20 m/s。M周围没有其他车辆，由式(1)～(4)和式(9)～(14)，以及表 2中参数计算得到图 7中的最优换道轨迹。

表 2 参考轨迹的换道工况2 Tab. 2 Lane change condition 2 of reference trajectory
平均车速/ (m·s -1) 车道 宽/m 最大纵向 车速/ (m·s -1) 最大加速度/ (m·s -2) 最大加加速度/ (m·s -3)
原始车道 目标车道 纵向 横向 纵向 横向
20 30 3.75 30 5 2 2 1
表选项
图 7 最优换道轨迹2(单位：m) Fig. 7 Optimal lane change trajectory 2(unit:m)
图选项

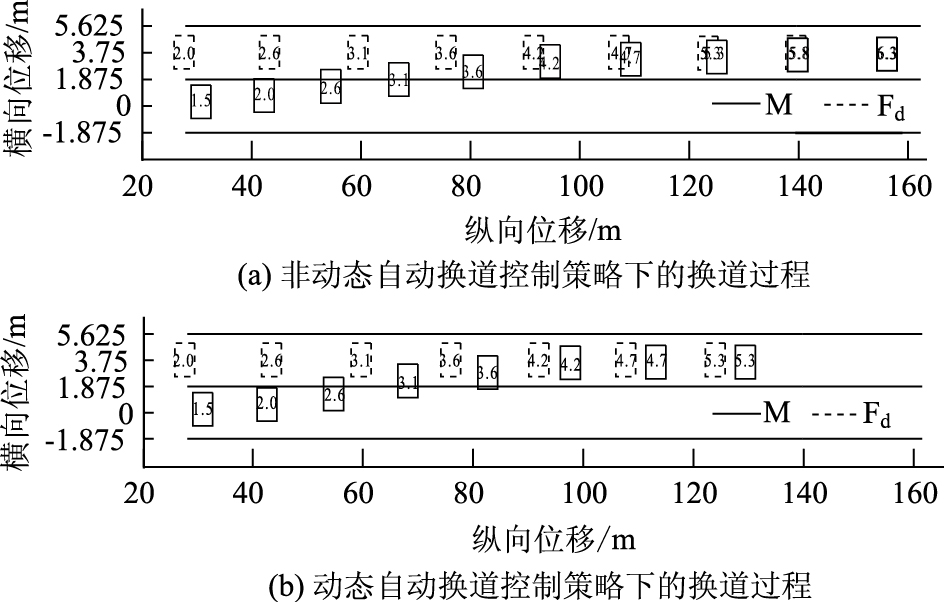
M沿着该最优轨迹换道的过程中，当进行到1.5 s 时，目标车道后面17 m处突然出现Fd，并且此时Fd以vFd=30 m/s的车速匀速行驶。按照M当前的换道轨迹和Fd的运动状态，由式(6)计算出对应的最小安全距离MSSFd,M为17.29 m。由式(15)可知，沿着原来的轨迹行驶在4.5 s附近有碰撞危险，如图 8(a) 。因而需要对M的换道轨迹进行重新规划。增加式(15)中的约束条件后，依据式(1)和式(9)～(15)重新规划换道轨迹后的换道过程如图 8(b)所示，车辆之间没有碰撞危险，M能安全地完成换道。

图 8 Fd影响下不同换道过程对比 Fig. 8 Comparison of different lane changes under influence of Fd
图选项

和最优换道过程相比，换道时间明显缩短，驶过的纵向换道距离也缩短，避免了和Fd的潜在碰撞。因为在新的换道过程中，M需要在加速的同时增大方向盘转角，才能保持和Fd之间的距离，实现安全换道。

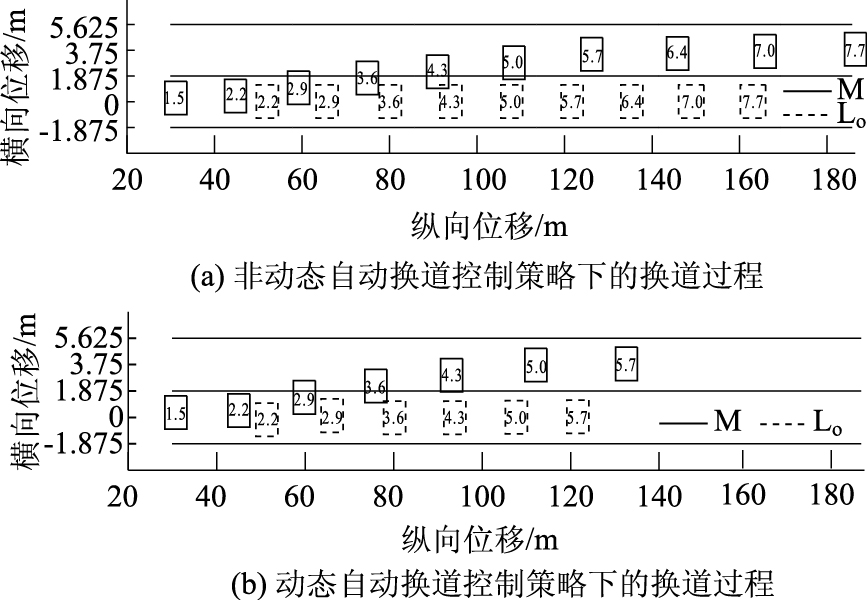
类似地，当M换道进行到1.5 s时，原始车道前面出现离其比较近的Lo(M与Lo距离为5 m)，并且此时Lo以vLo=20 m/s的车速匀速行驶，计算得到所应该保持的安全车间距为7.01 m。为避免图 9(a)中在3 s附近可能发生的碰撞危险，对M的换道轨迹进行重新规划。依据式(1)和式(9)～(15)重新规划换道轨迹后的换道过程如图 9(b)所示，M和Lo之间始终保持安全车距，没有碰撞危险。

和最优换道过程相比，换道时间更长，驶过的纵向换道距离也更长，但可以避免和突然切入的Lo之间的碰撞，因为M和Lo之间距离很小，M不能通过猛打方向盘来避免和Lo的潜在碰撞，而只能通过先减速来实现安全换道。

图 9 Lo影响下的不同换道过程对比 Fig. 9 Comparison of different lane changes under influence of Lo
图选项
4 结 论

本文对自动换道控制策略进行了研究，从上述研究结果可以得出以下几个结论：

(1)提出了基于车-车通信的自动换道控制策略，实现了安全舒适的自动换道过程，并优化了换道时间和换道驶过的纵向距离。

(2)实时动态的自动换道控制策略能适应周围车辆运动状态的变化，解决了换道过程中周围车辆切入带来的安全问题。

(3)提出的基于带约束的非线性优化问题的换道轨迹规划方法在换道初始时刻和换道过程中均能规划相应的换道轨迹。

在上述关于自动换道控制策略所取得的理论研究成果基础上，今后将在研究中搭建实车试验平台，进行测试验证，并对信息获取的准确度以及时效性对控制策略的有效性进行验证和研究。

参考文献
[1] VAN DIJCK T, VAN DER HEIJDEN G A J. Visionsense:An Advanced Lateral Collision Warning System[C]//IEEE Intelligent Vehicles Symposium. Piscataway:IEEE, 2005:296-301.
[2] 杨晓光,黄罗毅,王吟松,等. 基于车车通信的换道超车辅助系统设计与实现[J]. 公路交通科技,2012,29(11):120-124. YANG Xiao-guang, HUANG Luo-yi, WANG Yin-song, et al. A Novel Lane Change and Overtaking Assist System Design and Implementation Based on Vehicle-to-vehicle Communication[J]. Journal of Highway and Transportation Research and Development, 2012, 29(11):120-124.
[3] CHEE W, TOMIZUKA M. Vehicle Lane Change Maneuver in Automated Highway Systems, UCB-ITS-PRR-94-22[R]. Berkeley:California Partners for Advanced Transit and Highways(PATH), 1994.
[4] 李玮,高德芝,段建民. 智能车辆自由换道模型研究[J]. 公路交通科技,2010,27(2):119-123. LI Wei, GAO De-zhi, DUAN Jian-min. Research on Lane Change Model for Intelligent Vehicles[J]. Journal of Highway and Transportation Research and Development, 2010, 27(2):119-123.
[5] PETROV P, NASHASHIBI F. Adaptive Steering Control for Autonomous Lane Change Maneuver[C]//IEEE Intelligent Vehicles Symposium. Piscataway:IEEE, 2013:835-840.
[6] PAPADIMITRIOU I, TOMIZUKA M. Fast Lane Changing Computations Using Polynomials[C]//Proceedings of the 2003 American Control Conference, 2003, 41(1):48-53.
[7] 游峰.智能车辆自动换道与自动超车控制方法的研究[D]. 长春:吉林大学, 2005. YOU Feng. Study on Autonomous Lane Changing and Autonomous Overtaking Control Method of Intelligent Vehicle[D]. Changchun:Jilin University, 2005.
[8] FENG J, RUAN J, LI Y. Study on Intelligent Vehicle Lane Change Path Planning and Control Simulation[C]//2006 IEEE International Conference on Information Acquisition. Piscataway:IEEE, 2006:683-688.
[9] 李玮, 王晶, 段建民. 基于多项式的智能车辆换道轨迹规划[J]. 计算机工程与应用, 2012, 48(3):242-245.LI Wei, WANG Jing, DUAN Jian-min. Lane Changing Trajectory Planning of Intelligent Vehicles Based on Polynomials[J]. Computer Engineering and Applications, 2012, 48(3):242-245.
[10] 马川, 曹凯. 基于多项式理论智能车辆轨迹规划[J]. 农业装备与车辆工程, 2013, 51(3):17-21. MA Chuan, CAO Kai. Intelligent Vehicle Trajectory Planning Based on Polynomial Theory[J]. Agriculture Equipment & Vehicle Engineering, 2013, 51(3):17-21.
[11] HULT R, TABAR R S. Path Planning for Highly Automated Vehicles[D]. Gothenburg:Chalmers University of Technology, 2013.
[12] JULA H, KOSMATOPOULOS E B, IOANNOU P A. Collision Avoidance Analysis for Lane Changing and Merging[J].
[13] 王江锋,邵春福,闫学东,等. 基于虚拟现实的车辆换道最小安全距离研究[J]. 公路交通科技,2010,27(8):109-113. WANG Jiang-feng, SHAO Chun-fu, YAN Xue-dong, et al. Research on Minimum Safety Distance of Lane Changing Based on Virtual Reality[J]. Journal of Highway and Transportation Research and Development, 2010, 27(8):109-113.
[14] KHODAYARI A, GHAFFARI A, AMELI S, et al. A Historical Review on Lateral and Longitudinal Control of Autonomous Vehicle Motions[C]//2nd International Conference on Mechanical and Electrical Technology(ICMET). Piscataway:IEEE, 2010:421-429.
[15] SOLEA R, NUNES U. Trajectory Planning and Sliding-mode Control Based Trajectory-tracking for Cybercars[J]. Integrated Computer Aided Engineering, 2007, 14(1):33-47.
[16] 叶涛,侯增广,谭民,等. 移动机器人的滑模轨迹跟踪控制[J]. 高科技通讯,2004,14(1):71-74. YE Tao, HOU Zeng-guang, TAN Min, et al. Sliding Mode Trajectory Tracking Control of Mobile Robots[J]. High Technology Letters, 2004, 14(1):71-74.