扩展功能
文章信息
- 唐夕茹, 徐丽萍
- TANG Xi-ru, XU Li-ping
- 基于改进型元胞自动机模型的双车道公路交通冲突分析
- Analysis of Traffic Conflict in Two-lane Highway Based on Improved CA Model
- 公路交通科技, 2016, Vol. 33 (3): 109-115
- Journal of Highway and Transportation Research and Denelopment, 2016, Vol. 33 (3): 109-115
- 10.3969/j.issn.1002-0268.2016.03.018
-
文章历史
- 收稿日期: 2014-05-30
2. 城市交通节能减排检测与评估北京市重点实验室, 北京 100035
2. Beijing Key Laborary of Urban Traffic Energy Saving and Emission Reduction Detection and Assessment, Beijing 100035, China
交通冲突是交通行为者在参与道路交通过程中,与其他交通行为者发生相会、超越、交错、追尾等交通遭遇时,有可能导致发生交通损害危险的交通现象[1]。交通冲突的实质是交通行为不安全因素的表现形式,其发展既可能导致事故发生,也可能因采取的避险行为得当而避免事故发生,因而事故与冲突存在着极为相似的形式,两者的唯一差别在于是否发生了直接的损害性后果。交通工程学者认为交通冲突技术是鉴别事故黑点的有效手段[2, 3]。
目前,国内外对交通冲突的研究重点是冲突与事故的相互关系、冲突判别方法和预测、利用冲突的交通安全评价[4, 5],而在实际应用中对冲突数据的获取仍采用简单的距离判别法、时间判别法,甚至是粗略的目测法[6]。这些方法适合对特定对象进行定点观测,大范围冲突数据获取困难且投入成本高,非常不适合对以公路网为代表的大范围路网进行观测。
元胞自动机(Cellular Automaton,CA)交通流模型灵活地引入描述真实交通条件的各种参量,能够有效模拟交通流中车辆的微观运动,便于研究车辆间的相互作用机理,因此在交通流理论的研究中得到广泛应用[7, 8]。本文利用元胞自动机交通流模型,对公路交通特征进行模拟,分析公路交通冲突的属性特征,以此实现以冲突为指标的公路危险状态判别。
1 改进的双车道元胞自动机模型在双车道公路中,按照车辆的爬坡性能可以将车辆分为大车和小车两类。对于驾驶员而言,在以往的研究中,根据驾驶员的性格,将驾驶员分为激进型和保守型[9]。激进型驾驶员在拥挤条件下,会比保守型驾驶员更容易超车,且只要有足够的前车间距,就会尽可能加速;而保守型驾驶员则会与前车保持较大的距离,且超车较少。
根据以上条件,可以在行驶演化规则中区分激进型和保守型驾驶员的规则,给出双车道公路CA规则。
1.1 车辆正向行驶演化规则(1)对于保守型的车辆,按NaSch模型演化规则[9]得出正向行驶车辆演化规则如下。
在t+1时刻,路段上的车辆速度为:
① 若 Vi(t)<gapi(t),Vi(t)<Vimax,则
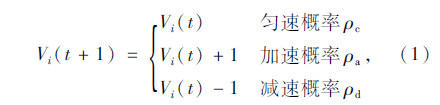
② 若 Vi(t)<gapi(t),Vi(t)=Vimax,则
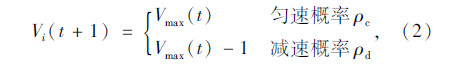
③ Vi(t)≥gapi(t),若满足超车规则,则遵循超车规则;若不满足超车规则,则
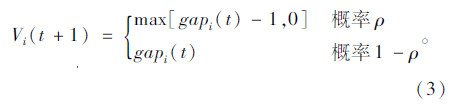
在t+1时刻,路段上的车辆位置为:
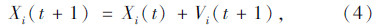
(2)对于激进型的车辆,按FI模型演化规则[10]得出正向行驶车辆演化规则如下。
在t+1时刻,路段上的车辆速度为:
①若 Vi(t)<gapi(t),Vi(t)<Vimax,则

②若 Vi(t)<gapi(t),Vi(t)=Vimax, 则
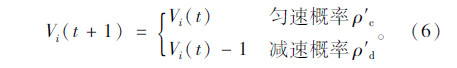
③ Vi(t)≥gapi(t),若满足超车规则,则后车超车。若不满足超车规则,则
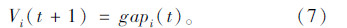
在t+1时刻,路段上车辆的位置为:
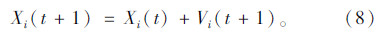
在超车过程中,超车车辆的速度低于其最大速度时,激进型驾驶员直接加速到最大车速,保守型驾驶员每时步速度加1格点/时步;当达到最大速度时,以最大速度匀速行驶。同时,在超车过程中低速车队列中的车辆若满足超车条件,可紧随超车车辆超车,其头车作匀速或减速运动。超车过程如图 1所示。

|
| 图 1超车过程 Fig. 1 Process of overtaking |
此时,超车规则如下。
(1)当前车受到本道前方的低速车队列阻碍时:
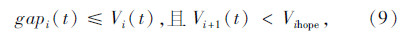
(2)在当前车的超车视距内,低速车队列前有足够的空间时:
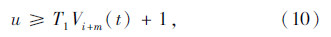
(3)在当前车的超车视距内邻道前方有足够的空间,使得逆向行驶的最长时间T2大于逆向行驶的最短时间T1。
(4)若满足以上3个条件,当前车以概率ρT换道超车。
换道速度如下。
①对于保守型车辆:
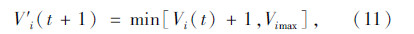
② 对于激进型车辆:
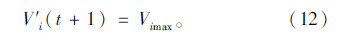
换道车辆的位置:
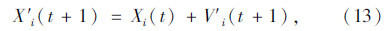
在超车过程中,超车视距内邻道与超车车辆迎面行驶的紧邻车辆作匀速运动,且其后方车辆不对它超车,当迎面行驶车辆可能阻碍超车运行时,作减速规避。
此时,超车逆行规则如下。
逆行速度:

车辆更新位置:
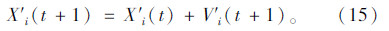
由于是双车道公路,超车需要借助对向车道,属于逆行,因此不能在对向车道上停留过长时间,因此车辆在对向车道停留的时间会有一个时间上限和时间下限。
超车逆行的车辆在对向车道停留的时间下限T1为:
当γ>0时,若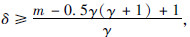 则
则
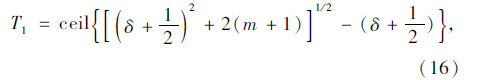
若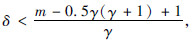 则则
则则
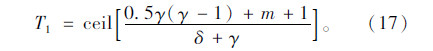
当γ=0时,
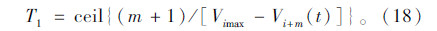
超车逆行的车辆在对向车道停留的时间上限T2为:
当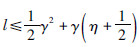 时,
时,
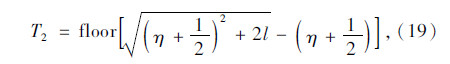
当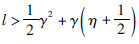 时,
时,
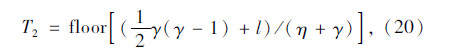
当车辆在对向车道行驶时间达到T1时,完成超车回到本车道。
2 双车道元胞自动机模型的冲突标定借鉴安全间接分析模型(SSAM)的冲突判别原理[11],对元胞自动机模型中的冲突判别方法进行标定。从前文的分析可知,严重交通冲突与交通事故有着直接的相关性,因此在元胞自动机对交通冲突判定上直接利用严重交通冲突的参数进行标定。
通过调研发现,严重冲突对应的交通状态数据既包括高速度、短距离、正向冲突,也可能包括低速度、短距离、正向冲突和高速度、长距离、正向冲突。由此可知,与距离、速度直接相关的加速度是最关键因素。因此,本文在判别严重交通冲突时,将车辆避险时采用的最大加速度作为判别依据。
对严重交通冲突的判定过程如下。
(1)同一车道同向行驶的车辆
设定车辆的最大加速度为a(对于不同车型加速度不同),最大减速度为a′,在t时刻,前后两车的位置分别为xA,xB,前后两车的速度分别为VA,VB。则在t+1时刻,前后两车可能的位置范围为:
前车: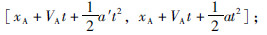
后车: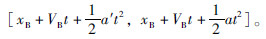
根据前后两车的位置范围(如图 2所示),判定是否有范围交集,如果范围存在重叠部分,则可能发生冲突。在此基础上,如果后车采用最大加速度进行减速时,后车的位置仍在重叠部分,则记为一次严重冲突。
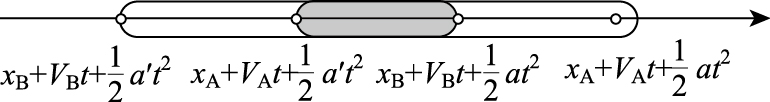
|
| 图 2 车辆位置范围示意图 Fig. 2 Schematic diagram of vehicle position range |
(2)逆向超车车辆
按照元胞自动机模型设置的超车规则和超车保护规则,在当前车的超车视距内,低速车队列前有足够的空间 (u≥T1Vi+m(t)+1),同时在当前车的超车视距内邻道前方有足够的空间,使得T2>T1时,可进行逆向超车。在逆向超车的冲突判别时,可以采用临界状态下的逆向超车规则作为冲突的判定条件,即u=T1Vi+m(t)+1,且T2>T1时,超车记为一次严重冲突。
3 数值模拟 3.1 参数标定考虑到公路上的车辆类型,大车与小车的车长差距较大,为了更真实地描述实际情况,将模型的基础条件设置如下:元胞长度3.5 m(记为1格点)、双向两车道、小车的最大车速Vmax=8格点/时步,大车的最大车速V′max=4格点/时步,期望速度Vihope为车辆保持匀速行驶时的速度,模拟的1时步为1 s。模型的其他参数设置如下。
(1)设置道路长度L为1 000 个元胞(即3.5 km);采用开放式边界条件,初始条件车道为空,将道路入口处第 1个元胞设置为发车区,车辆到达服从泊松分布,到达系数为λ。
(2)车辆进入路段的初始速度:大车满足均值为2,方差为1.3的正态分布;小车满足均值为4,方差为1.84的正态分布(数值来源为北京市平谷县S230路段实测获取)。
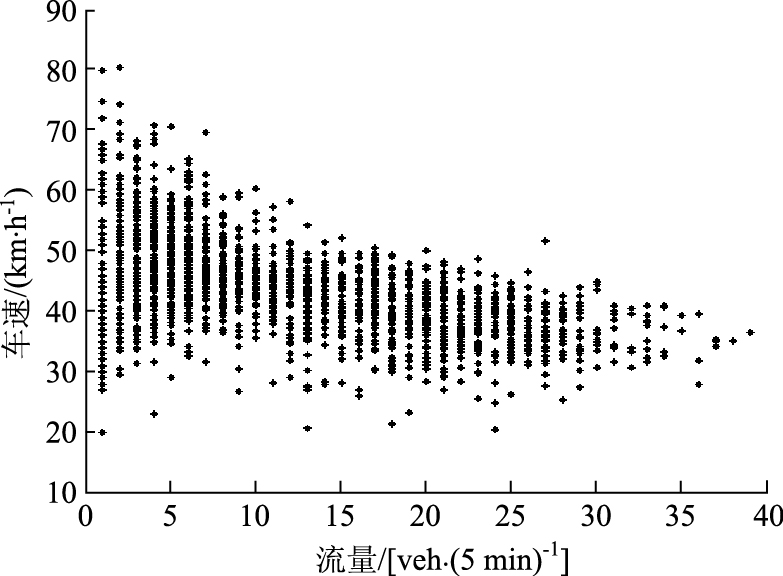
3.2 与实测数据对比图 3为北京市平谷县S230路段每5 min实测数据的平均速度-流量关系图。图中的数据是以2010年9月全月的流量、车速为样本,剔除观测周期(5 min) 无流量情况的数据。可以看出,对于双车道公路,由于其在交通运输中的地位,正常情况下其承担的交通量并不是很大,因此除受到交通事故等外界干扰,很难观测到道路出现阻塞流的情况。此外,由于道路承担较大一部分的货运运输,货车在道路车型中占较大比例,受到大货车加速度较小、爬坡性能较弱的制约。在车流较小时,路段车速与其交通组成有极大关系,其取值非常分散;在流量增大时,车速会呈现中心聚拢的趋势。这与常见的高速公路流量-速度关系有一定的区别。
|
| 图 3 实测速度-流量散点图 Fig. 3 Measured speed-volume scattergram |
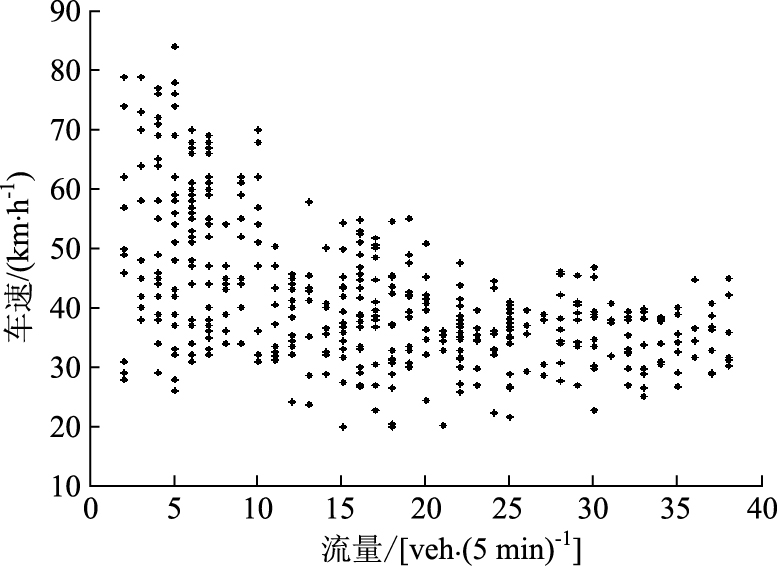
图 4为改进的双车道元胞自动机模型的仿真结果。在参数标定时,为了模拟不同流量的情况,车辆到达系数取值范围为[0.1,1],小型车比例选取值范围为[0,1],激进型驾驶员比例取值范围为[0,1],上述3个参数随机设定。同时, 为了与实测数据保持一致,模拟结果取路段中间格点(第500个元胞)计算断面的交通参数,计算统计时间间隔与实测数据一致(为5 min)。为消除暂态影响和更新车辆对交通流的迟滞影响,模拟结果前4 000时步不记录到输出结果中。
|
| 图 4 模拟速度-流量散点图 Fig. 4 Simulated speed-volume scattergram |
对比图 3与图 4可知,改进的双车道元胞自动机模型能够模拟各种情况的双车道交通状态,且模型输出结果的速度-流量关系与实测数据符合很好。
3.3 车道流量对称情况下的交通冲突分析对车辆到达系数λ从0.1到1.0,按照0.1的增长刻度分别对不同车型比例下和不同驾驶员比例下的公路交通特征进行模拟,求算冲突次数。为了消除系统随机性的影响,模型每次演化10 000时步,取4 000到8 000时步中每一时步的平均值,再对这4 000个平均值根据时间做系统平均。
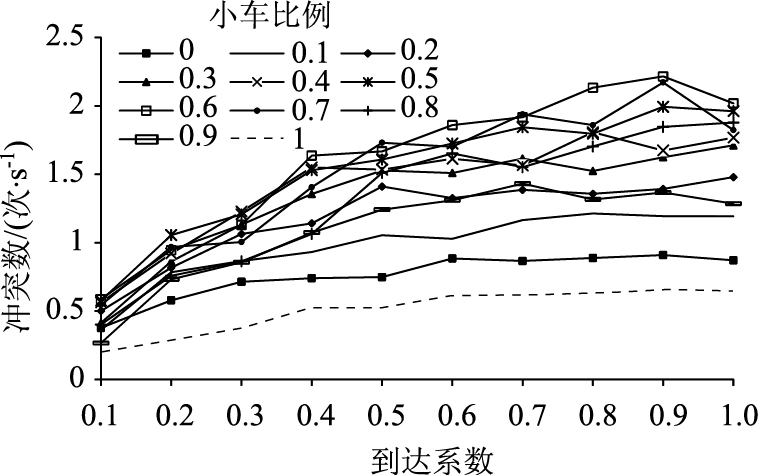
在模拟不同车型比例下的公路交通特征时,驾驶员比例按照激进与保守各占50%标定;在模拟不同驾驶员比例下的公路交通特征时,小车与大车比例各占50%。由于两条车道上车辆的到达系数一致,车道的交通特征也近似相同,因此取车道1的交通参数进行分析,得到如图 5、图 6的分析结果。
|
| 图 5 冲突数与到达系数关系图(车型) Fig. 5 Relationship between number of conflicts and arrival coefficient (vehicle type) |
|
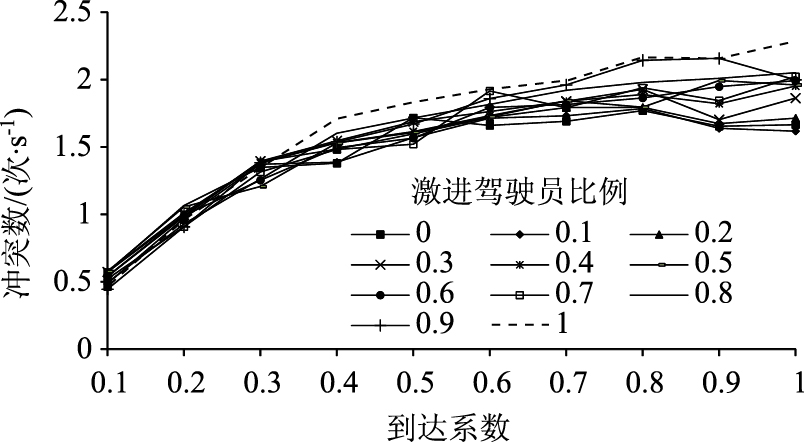
| 图 6 冲突数与到达系数关系图(驾驶员) Fig. 6 Relationship between number of conflicts and arrival coefficient (driver) |
图 5和6分别为不同车型比例和不同驾驶员比例下,冲突数与到达系数的关系图。
在图 5中,冲突数随着到达系数的增加而增大,不同小车比例的冲突数曲线分散非常明显,在车型单纯的情况下(小车比例为1或者0时),冲突数最低,小车比例为0.6和0.7时冲突数最高,可见在道路车辆运行不稳定时发生交通事故的概率比稳定时明显偏大。随着到达系数的增加,路段上车辆增多,车辆间相互影响的次数增加,冲突数增多,这也符合现实情况。
在图 6中,冲突数随着到达系数的增加而增大,对于不同驾驶员比例,在到达系数为0.3以上时曲线开始发散,当激进型驾驶员比例为1(即全为激进型驾驶员)时,冲突数最大且随到达系数的增加而增长最为迅速。
3.4 车道流量非对称情况下的交通冲突分析对车道2车辆到达系数λ保持0.8,车道1车辆到达系数λ从0.1到0.7,按照0.1的增长刻度分别对不同车型比例和不同驾驶员比例下的公路交通特征进行模拟,求算冲突次数。为了消除系统随机性的影响,模型每一次演化10 000时步,取4 000到8 000 时步中每一时步的平均值,再对这4 000个平均值根据时间做系统平均。
在模拟不同车型比例下的公路交通特征时,将驾驶员比例按照激进驾驶员比例标定为70%,保守驾驶员比例占30%;在模拟驾驶员比例下的公路交通特征时,小车比例占70%,大车比例占50%,得到如图 7、图 8的分析结果(即不同车型比例和不同驾驶员比例下,冲突数与到达系数的关系图)。
|
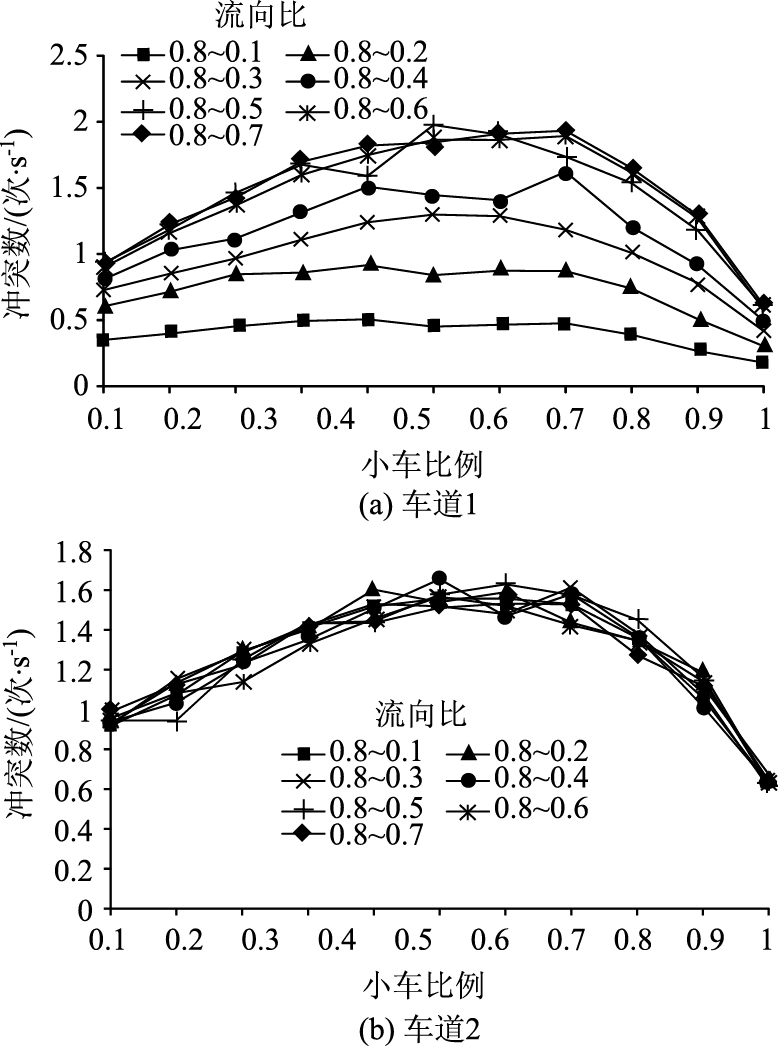
| 图 7 小车比例与冲突数关系图 Fig. 7 Relationship between proportion of small vehicles and number of conflicts |
|
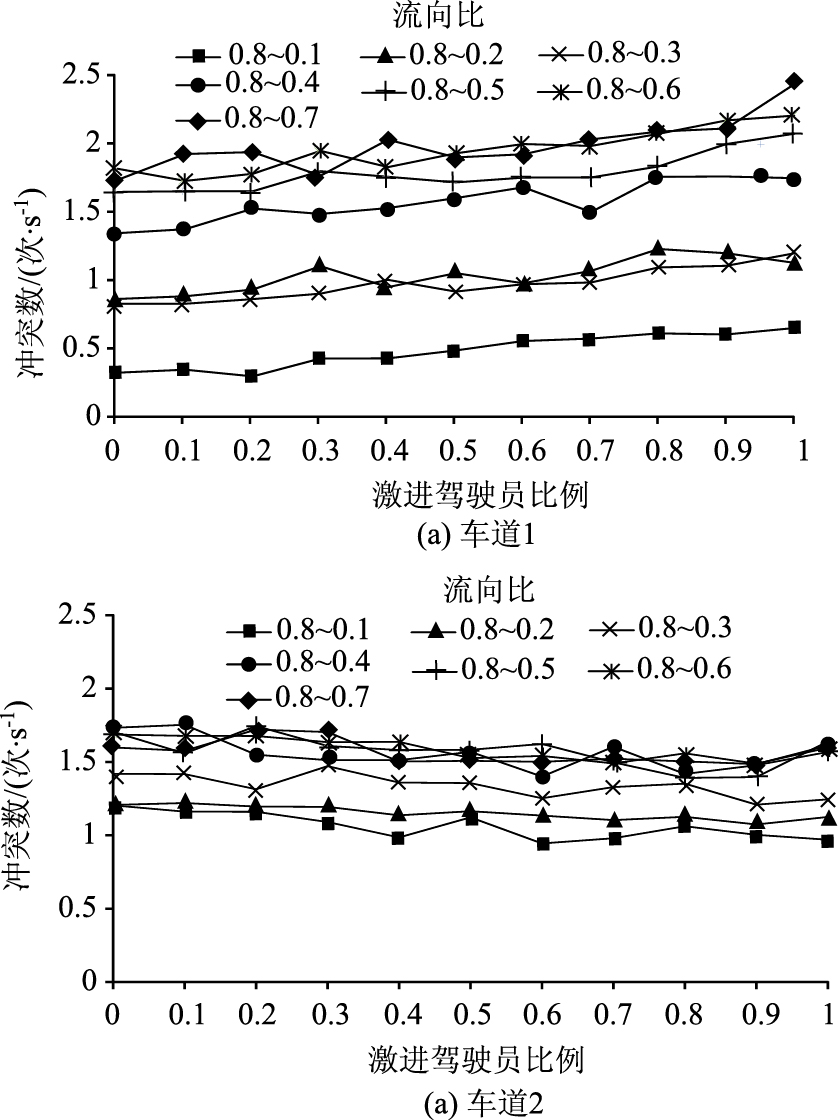
| 图 8 驾驶员比例与冲突数关系图 Fig. 8 Relationship between proportion of vehicles and number of conflicts |
在图 7中,对于低到达系数的车道1,冲突数随着到达系数的增加而增大,曲线呈类抛物线形,对于到达系数在0.3以上的曲线,抛物线的顶点对应的小车比例为0.7;当到达系数小于0.3时,抛物线顶点对应的小车比例逐渐从0.5演化到0.7。此外,随着到达系数的增加,冲突数整体的增加也非常明显。对于高到达系数的车道2,冲突数随着小车比例的增加,曲线呈类抛物线形,抛物线的顶点对应的小车比例为0.7,不同流向比下的曲线非常相近。可见,不同流向比下,小车比例对低流量道路冲突数的影响非常显著,而对高流量道路影响不明显。
在图 8中,对于低到达系数的车道1,冲突数随着激进型驾驶员比例的增加而增加的趋势非常明显。在到达系数为0.1时,由于路段车辆少,尽管超车人数多,但严重冲突发生的次数仍然处于最低水平;在到达系数为0.2和0.3时,冲突数比最低水平有较大增加,但两条曲线比较相近地处于中等水平;在到达系数大于0.3时,道路流量增大到一定程度,车辆间相互作用增强,车辆加、减速和超车越发困难,冲突次数又一次显著提高,且随着激进型驾驶员的增加,车辆强行超车次数增多,冲突数增加迅速,此时车道1流量虽小但冲突数明显高于大流量的车道2。对于高到达系数的车道2,曲线波动平稳,冲突数随驾驶员增加的变化不甚明显,但随着流向比的变化,对向车道到达系数的增加也会增加本车道的冲突数。
3.5 冲突数与其他交通参数的相关性分析上文已经分别讨论了车流对称和非对称情况下不同到达系数、不同驾驶员性格、不同车型比例的冲突数,并且定性解说了不同参数对交通冲突数的影响,而这些因素是综合作用于交通冲突的,因此,本文采用方差分析确定各因素与交通冲突的相关性情况。分析结果如表 1所示。
| 偏差来源 | 偏差 平方和 | 自由度 | 方差 | F检验值 | 显著性 水平 |
| 因素方差 分析模型 | 71.185 | 36 | 1.977 | 88.087 | 0 |
| 47.015 | 1 | 47.015 | 2 094.430 | 0 | |
| 到达系数 | 25.481 | 9 | 2.831 | 126.124 | 0 |
| 流向比 | 0.859 | 3 | 0.286 | 12.762 | 0 |
| 小车比例 | 14.716 | 10 | 1.472 | 65.558 | 0 |
| 激进型驾驶 员比例 | 1.694 | 10 | 0.169 | 7.546 | 0 |
| 误差 | 7.565 | 337 | 0.022 | ||
| 总和 | 656.598 | 374 | |||
| 总离差 | 78.750 | 373 | |||
| 注:1. 黑体数值的拟合优度=0.904 (调整的拟合优度=0.894); 2. 因变量为交通冲突数。 | |||||
由表 1可知,模型的拟合优度R2=0.904,表明方差分析的拟合结果极好;各因素的显著性水平均小于0.005,表明到达系数、小车比例、激进型驾驶员比例这4个因素对交通冲突有显著影响。
4 结 论本文根据双车道公路的交通流特性,充分考虑车辆的驾驶员具有不同的性格特征,以双车道元胞模型为基础,建立了改进型双向双车道元胞自动机模型。同时,采用开放边界条件进行数值模拟,真实地重现了不同性格和不同驾驶员比例情况下的交通状况。结果表明,公路交通冲突次数与车辆到达系数、流向比、小车比例、激进型驾驶员比例都有较强的相关性。在一般情况下,非对称流量条件下的冲突数比对称流量条件下整体要高,冲突数随着到达系数的增加而增大,且在一定范围内冲突数最大且随到达系数的增加而增长最为迅速。此外,随着激进型驾驶员的增加,冲突数也会增加。
| [1] | 海顿C. 交通冲突技术[M].张苏,译.成都:西南交通大学出版社,1994. HYDEN C. Traffic Conflicts Technique[M]. ZHANG Su, translated. Chengdu:Southwest Jiaotong University Press,1994. |
| [2] | 张苏. 中国交通冲突技术[M].成都:西南交通大学出版社,1998:5-10. ZHANG Su. Traffic Conflict Technique in China[M]. Chengdu:Southwest Jiaotong University Press,1998:5-10. |
| [3] | 成卫. 城市交通冲突技术理论与应用[M]. 北京:科学出版社, 2006. CHENG Wei. Theory and Application of Urban Traffic Conflict Technology[M]. Beijing:Science Press, 2006. |
| [4] | 曲昭伟, 李志慧, 胡宏宇, 等. 基于视频处理的无信号交叉口交通冲突自动判别方法[J]. 吉林大学学报:工学版, 2009, 39(增2):163-167. QU Zhao-wei, LI Zhi-hui, HU Hong-yu, et al. Traffic Conflict Automatic Discrimination at Non-signalized Intersection Based on Video Processing[J]. Journal of Jilin University:Engineering and Technology Edition, 2009,39(S2):163-167. |
| [5] | 王学明,姜华平,吴伟阳. 基于交通冲突技术的非机动车交通安全研究[J].公路交通科技, 2011, 28(增1):110-114. WANG Xue-ming, JIANG Hua-ping, WU Wei-yang. Traffic Safety of Non-motorized Vehicle Based on Traffic Conflict Technique[J]. Journal of Highway and Transportation Research and Development, 2011, 28(S1):110-114. |
| [6] | 张学亮, 邓卫, 郭唐仪. 基于冲突率的交叉口交通安全评价方法研究[J]. 交通运输工程与信息学报, 2007,5(1):85-90. ZHANG Xue-liang, DENG Wei, GUO Tang-yi. Development of Traffic Safety Evaluation Method Based on TCT at Grade Crossings[J]. Journal of Transportation Engineering and Information, 2007,5(1):85-90. |
| [7] | BARLOVIC R, SANTEN L, SCHADSCHNEIDER A, et al. Metastable States in Cellular Automata for Traffic Flow[J]. Physics of Condensed Matter, 1998, 5(3):793-800. |
| [8] | 史丹丹,朱正旺,刘好德. 考虑车-车通信的双车道元胞自动机交通流模型[J].公路交通科技,2009, 26(增1):142-146. SHI Dan-dan, ZHU Zheng-wang, LIU Hao-de. A Cellular Automaton Model of Traffic Flow Considering Vehicle-vehicle Communication[J]. Journal of Highway and Transportation Research and Development, 2009,26(S1):142-146. |
| [9] | CHEYBANI S, KERTÉSZ J, SCHRECKENBERG M. Stochastic Boundary Conditions in the Deterministic Nagel-Schreckenberg Traffic Model[J]. Physical Review E, 2001, 63(1):113-130. |
| [10] | 吴可非, 邝华, 孔令江, 等. 元胞自动机FI和NS交通流混合模型的研究[J]. 广西师范大学学报:自然科学版,2005(4):8-12. WU Ke-fei, KUANG Hua, KONG Ling-jiang, et al. Study of a Cellular Automaton FI-and-NS Mixed Model for Traffic Flow[J]. Journal of Guangxi Normal University:Natural Science Edition, 2005(4):8-12. |
| [11] | TRENTACOSTE M F.Surrogate Safety Measures from Traffic Simulation Models[M]. McLean, Virginia:U.S. Department of Transportation Federal Adminis-tration Research, Development and Technology, 2003:79-96. |
 2016, Vol. 33
2016, Vol. 33
