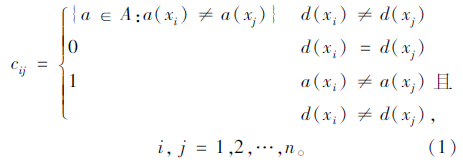扩展功能
文章信息
- 孟祥海, 覃薇, 邓晓庆
- MENG Xiang-hai, QIN Wei, DENG Xiao-qing
- 基于神经网络的山岭重丘区高速公路事故预测模型
- An Accident Prediction Model for Expressways in Mountainous and Rolling Areas Based on Neural Network
- 公路交通科技, 2016, Vol. 33 (3): 102-108
- Journal of Highway and Transportation Research and Denelopment, 2016, Vol. 33 (3): 102-108
- 10.3969/j.issn.1002-0268.2016.03.017
-
文章历史
- 收稿日期: 2015-05-04
山岭重丘区高速公路复杂的几何线形条件往往是诱发交通事故的重要原因之一[1, 2]。分析几何线形指标与交通事故之间的关系,并据此建立高速公路事故预测模型[3, 4, 5],探索交通事故发生的内在规律,对有针对性地提出安全改善对策具有重要意义[6]。
目前我国在道路交通事故预测方面尚未形成完整的、认可度较高的模型和方法体系。Poisson系列事故预测模型多存在数据组织复杂、模型精度较低的缺陷[7]。IHSDM预测模型虽具有良好的模型结构,但不大适用于交通环境差异较大的公路,且其参数标定也主要是基于美国的交通事故数据[8, 9]。基于统计学原理的事故预测模型一般均有自身的假设条件或预定义从属变量与独立变量之间的关系。而神经网络技术一般可不需要这种预定义,大量研究也证明了神经网络技术在处理预测和分类问题上的优势[10]。因此,本文基于我国山岭重丘区高速公路的几何线形条件、交通条件及交通事故数据,探讨基于神经网络的事故预测方法,并建立高速公路基本路段事故预测模型。
1 数据来源与数据描述 1.1 数据来源数据来源于辽宁省交通厅科技项目“高速公路运行安全研究”中的丹阜高速公路桃仙至丹东段(简称“沈丹高速公路”)和广东省交通运输厅科技项目“基于全社会成本的高速公路设计方案评价技术研究”中广东省境内的京珠高速公路粤北段(简称“京珠高速公路”)。沈丹高速公路桃仙至丹东段长66 km,双向四车道,设计速度100 km/h。京珠高速公路全长109.29 km,双向四车道,设计速度80 km/h。这两条高速公路均为典型的山岭重丘区高速公路。
1.2 数据描述依据上述两个课题所开发的“高速公路道路交通地理信息系统”和“高速公路交通事故地理信息系统”,提取出了本研究所需的交通事故、交通量(即年平均日交通量AADT)和几何线形指标数据,交通事故和交通量数据汇总见表 1。
| 区段编号 | 所属高速公路 | 起终点桩号 | 区段长度/km | 事故总数/起 | 事故统计起止年份 | AADT/(pcu·d-1) |
| 1 | 京珠高速公路 | K0+000~K11+925 | 11.925 | 157 | 2006~2009 | 25 549 |
| 2 | K11+925~K22+738 | 10.813 | 166 | 26 224 | ||
| 3 | K22+738~K52+791 | 30.035 | 419 | 19 350 | ||
| 4 | K52+791~K74+691 | 21.900 | 294 | 22 491 | ||
| 5 | K74+691~K86+685 | 11.994 | 172 | 25 743 | ||
| 6 | K86+685~K105+200 | 18.515 | 303 | 27 559 | ||
| 7 | K105+200~K109+292 | 4.092 | 53 | 21 337 | ||
| 8 | 沈丹高速公路 | K42+499~K72+307 | 29.808 | 1 350 | 2006~2012 | 9 097 |
| 9 | K72+307~K86+904 | 14.597 | 611 | 9 054 | ||
| 10 | K86+904~K98+011 | 11.107 | 271 | 8 657 | ||
| 11 | K98+011~K108+419 | 10. 408 | 361 | 9 574 |
两条高速公路2006—2009共发生4 318起交通事故,根据上述两个系统可提取出每起事故的发生原因并据此剔除明显与几何线形无关的事故(如超速、疲劳驾驶等)后,共有4 157起事故数据,这是建立事故预测模型的基础事故样本。提取出的几何线形指标共7个,包括直线长度、平曲线半径、平曲线偏角、竖曲线半径、竖曲线长度、坡长和纵坡坡度。交通事故与几何线形指标的匹配是通过两个地理信息系统中的里程桩号来链接实现的。
2 变量选择及事故预测单元 2.1 基于几何线形条件的路段单元划分本文拟依据几何线形条件来建立山岭重丘区高速公路基本路段的事故预测模型,为此,首先应根据几何线形条件对高速公路路段进行划分,形成路段单元。每个路段单元上的一组数据就是一个最基本的样本,是进行事故预测模型变量选择的基础,而路段单元本身也是构成事故预测单元的基础。
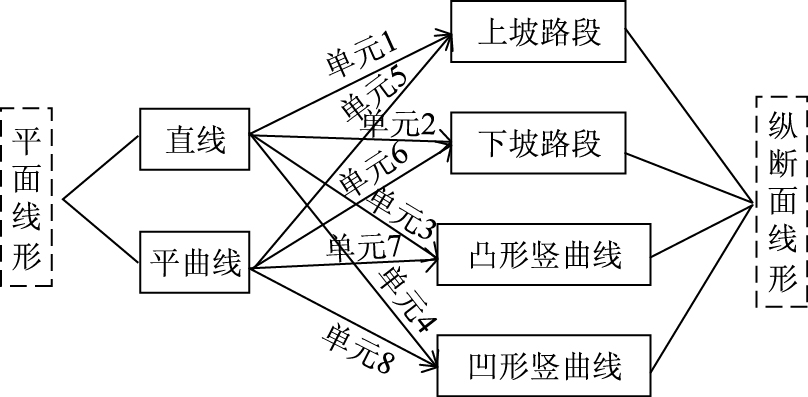
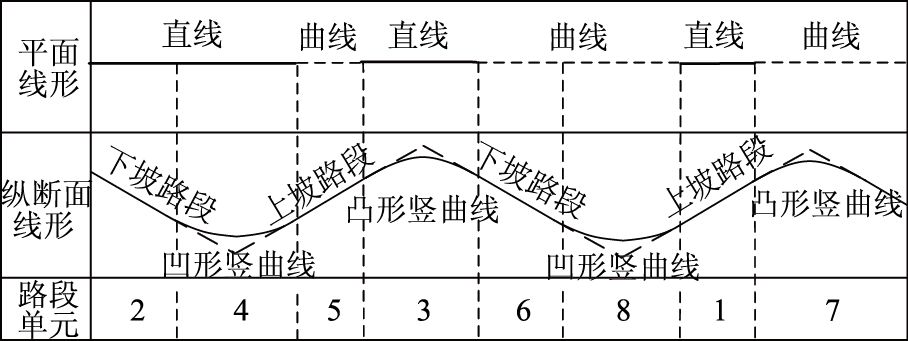
将平面线形分成直线和平曲线两大类,将纵断面线形分成上坡路段、下坡路段、凸形竖曲线和凹形竖曲线4类,则平纵组合后的路段单元有8种,分别为直线-上坡路段(路段单元1)、直线-下坡路段(路段单元2)、直线-凸形竖曲线路段(路段单元3)、直线-凹形竖曲线路段(路段单元4)、平曲线-上坡路段(路段单元5)、平曲线-下坡路段(路段单元6)、平曲线-凸形竖曲线路段(路段单元7)和平曲线-凹形竖曲线路段(路段单元8)。路段单元线形组合见图 1,路段单元划分示例见图 2。
|
| 图 1 路段单元线形组合 Fig. 1 Geometric alignment combination of sections |
|
| 图 2 路段单元划分示例 Fig. 2 Example of section division |
每个路段单元包括的几何信息有直线长度、平曲线半径、平曲线偏角、竖曲线半径、竖曲线长度、坡长、纵坡坡度,这7个变量就是变量选择时的初始变量。另外,每个路段单元还应有年平均日交通AADT信息和事故率数据,事故率采用的是每公里每车道的事故数。
2.2 基于粗糙集理论的变量选择变量选择就是在路段单元的8个变量(1个AADT变量和7个几何线形指标变量)中选择对交通事故发生有突出影响的变量。由于AADT是交通事故发生的前提和基础条件,因此该变量直接保留,不参与变量选择。此时,变量选择主要是筛选几何线形指标变量。
粗糙集理论是一种用来处理不完整和模糊性数据的数学工具[11],其属性约简过程就是变量筛选过程。本文利用基于可辨识矩阵的约简算法来进行几何线形指标变量的选择。
设S=(U,A)是路段单元几何线形数据系统,U={x1,x2,…,xn},xi为第i个路段单元,共有n个路段单元。A={a1,a2,…,a7},a1到a7分别为相应路段单元的7个线形指标变量。设D={d,d(x2),…,d(xn)},d(xi) 为路段单元i的事故率,矩阵M(S)=(cij)n×n为几何线形数据系统S的可辨识矩阵,可辨识矩阵元素cij取值如下:
可辨识矩阵元素cij就是能使路段单元xi与路段单元xj区别开的所有几何线形指标变量的集合,取a1∨a2∨…∨a7的析取范式。显然,把xi与xi+1,xi+2,…,xn区分开的变量应该为合取式ci(i+1)∧ci(i+2)∧…∧cin,则所有可辨识矩阵元素的合取式能将所有路段单元两两区分开。
利用Rosetta软件实现基于粗糙集理论的几何线形指标变量的筛选过程。将1 572个路段单元数据输入Rosetta软件中,并利用Johnson 算法对数据进行约简,共筛选出平曲线半径RP、纵坡坡度i、直线长度LZ、竖曲线长度LS这4个对路段事故发生有突出影响的几何线形指标变量。变量选择结果见表 2。
| 变量类别 | 变量选择结果 | 备注 |
| 交通量变量 | AADT | 直接保留的变量 |
| 几何线形指标变量 | 直线长度 | 基于粗糙集理论 选择出的变量 |
| 纵坡坡度 | ||
| 平曲线半径 | ||
| 竖曲线长度 |
按照变量选择后的几何线形指标进行平纵线形组合后(见图 3),将形成6类路段,这就是事故预测单元,分别为直线-上坡路段(预测单元1)、直线-下坡路段(预测单元2)、直线-竖曲线路段(预测单元3)、平曲线-上坡路段(预测单元4)、平曲线-下坡路段(预测单元5)、平曲线-竖曲线路段(预测单元6)。显然,事故预测单元是由基本路段单元构成的,且能涵盖所有基本路段单元。

|
| 图 3 事故预测单元线形组合 Fig. 3 Geometric alignment combination of accident prediction sections |
按照事故预测单元的定义对京珠高速公路和沈丹高速公路重新进行路段划分,共得到1 472个事故预测单元,详见表 3。这些事故预测单元构成了建立事故预测模型的样本空间。
| 事故预测单元 | 直线-上坡路段 | 直线-下坡路段 | 直线-竖曲线路段 | 平曲线-上坡路段 | 平曲线-下坡路段 | 平曲线-竖曲线路段 |
| 个数/个 | 125 | 94 | 215 | 233 | 271 | 534 |
所有预测单元均存在1个或1个以上的线形指标空值项(即Null项),例如,直线-上坡路段事故预测单元就会存在平曲线半径和竖曲线长度两个空值项。为了实现建立事故预测模型的目的并满足其算法的要求,需对所有空值项进行赋值。
本文的赋值思路是,假设事故预测单元中的无线形指标变量(空值项)均为理想线形条件,即按理想线形条件下的线形指标值对空值项进行赋值。理想的线形条件就是事故率最低时的线形指标值或取值范围。借鉴文献[12]的研究成果(该成果的数据包含京珠高速公路和沈丹高速公路),得到了山岭重丘区高速公路的理想线形条件,见表 4。
| 几何线形指标 | 理想线形条件的取值范围 |
| 直线长度(LZ)/km | 0.5<LZ<1.5 |
| 平曲线半径(RP)/m | RP>4 000 |
| 纵坡坡度(i)/% | 0<i<1 |
| 竖曲线长度(LS)/m | LS>1 500 |
对照表 4具体确定的赋值结果,直线长度空值项取理想线形条件下直线长度的均值(此处为1 000 m),平曲线半径、纵坡坡度、竖曲线长度等空值项分别取4 000 m,0.5%,1 500 m。表 5给出了京珠、沈丹两条高速公路上部分事故预测单元的原始线形指标数据及空值项赋值后的线形指标数据。
| 编号 | 预测单元类型 | 原始数据 | 赋值后数据 | ||||||
| 平曲线半径/m | 直线长度/m | 竖曲线长度/m | 纵坡/% | 平曲线半径/m | 直线长度/m | 竖曲线长度/m | 纵坡/% | ||
| 1 | 直线-竖曲线路段 | — | 212 | 183 | — | 4 000 | 212 | 183 | 0.5 |
| 2 | 直线-下坡路段 | — | 212 | — | -1.7 | 4 000 | 212 | 1 500 | -1.7 |
| 3 | 平曲线-竖曲线路段 | 1 200 | — | 1 500 | — | 1 200 | 1 000 | 1 500 | 0.5 |
| 4 | 平曲线-上坡路段 | 2 200 | — | — | 1.1 | 2 200 | 1 000 | 1 500 | 1.1 |
| 5 | 平曲线-竖曲线路段 | 3 000 | — | 500 | — | 3 000 | 1 000 | 500 | 0.5 |
| 6 | 平曲线-下坡路段 | 1 200 | — | — | -3.4 | 1 200 | 1 000 | 1 500 | -3.4 |
| 7 | 直线-上坡路段 | — | 1 526 | — | 1.08 | 4 000 | 1 526 | 1 500 | 1.08 |
| 8 | 平曲线-上坡路段 | 1 800 | — | — | 2.2 | 1 800 | 1 000 | 1 500 | 2.2 |
| | | | | | | | | | |
| 1 472 | 直线-竖曲线路段 | — | 1 526 | 1 500 | — | 4 000 | 1 526 | 1 500 | 0.5 |
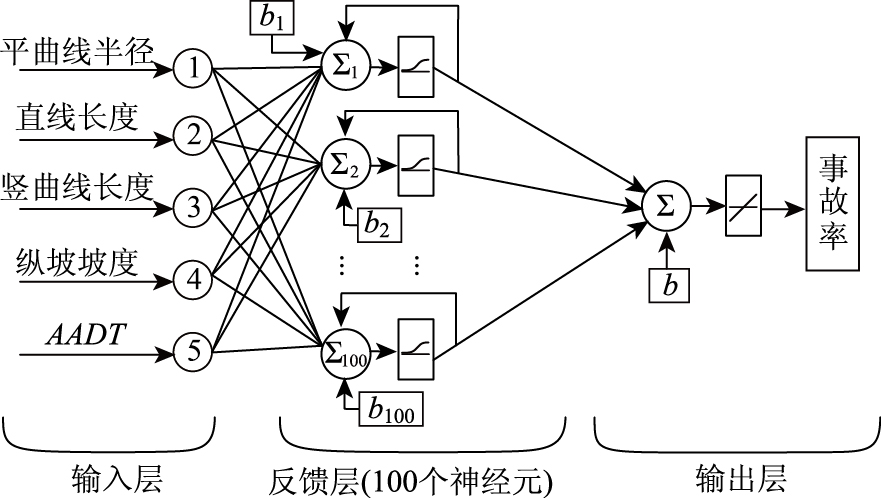
Elman神经网络是一种带反馈的两层神经网络,能以任意精度逼近任意函数,唯一的要求是其隐含层必须有足够的神经元,隐层中的神经元越多,网络逼近复杂函数的能力就越强。由于高速公路的事故率与几何线形之间存在复杂的非线性关系,而目标输出(即事故率)又是确定的,因此Elman神经网络适用于用来建立事故预测模型。本文建立的Elman神经网络事故预测模型的结构如图 4所示。
|
| 图 4 Elman神经网络事故预测模型的结构 Fig. 4 Structure of accident prediction model of Elman neural network |
本文应用MATLAB r2011b神经网络工具箱进行网络的分析和设计研究。
4.2 神经网络模型的训练与测试将京珠高速公路上的1 200个事故预测单元随机分成两组,第1组600个单元,用于网络训练;第2组600个单元,用于网络测试。网络训练精度为0.05,测试精度为0.16,测试结果见图 5。由图 5可知,预测事故率与实际事故率的相对误差小于20%的单元有377个,约占测试单元总数的63%,这说明训练好的模型对绝大多数单元均具有较高的预测精度。但同时也可看到,仍有11个单元(约占测试单元总数的1.83%)的预测事故率与实际事故率相差甚远,属于异常测试样本(见图 5 中的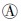 )。分析这些异常样本,本文认为除几何线形因素外,其实际事故率过高的原因可能主要来自人为原因、环境因素及一些随机性事件。总之,由测试结果可知,该网络的泛化能力还是较强的,可根据已确定的权值矩阵和偏置向量进行预测模型应用。
)。分析这些异常样本,本文认为除几何线形因素外,其实际事故率过高的原因可能主要来自人为原因、环境因素及一些随机性事件。总之,由测试结果可知,该网络的泛化能力还是较强的,可根据已确定的权值矩阵和偏置向量进行预测模型应用。
|
| 图 5 网络测试结果 Fig. 5 Result of network test |
用标定好的事故预测模型对各输入变量进行敏感性分析,确定出各线形指标和AADT与事故率的关系,并与基于实际数据统计得到的关系进行对比,从而判断该模型在机理上是否符合交通事故与几何线形之间的基本关系。
5.1 平曲线半径的敏感性分析涉及平曲线半径的路段共有3种,分别为平曲线-上坡路段、平曲线-下坡路段和平曲线-竖曲线路段。在进行敏感性分析时,平曲线半径是唯一变动的量,最小取值为500 m,然后按每级增加500 m 的方式设置平曲线半径的取值。AADT取样本均值,平曲线-下坡路段中坡度取所有下坡路段样本均值(此处为-2.118%),平曲线-上坡路段中坡度取所有上坡路段样本均值(此处为1.971%),平曲线-竖曲线路段中竖曲线长度取所有竖曲线路段样本均值(此处为505.767 m),其他几何线形指标取理想线形条件的指标值。
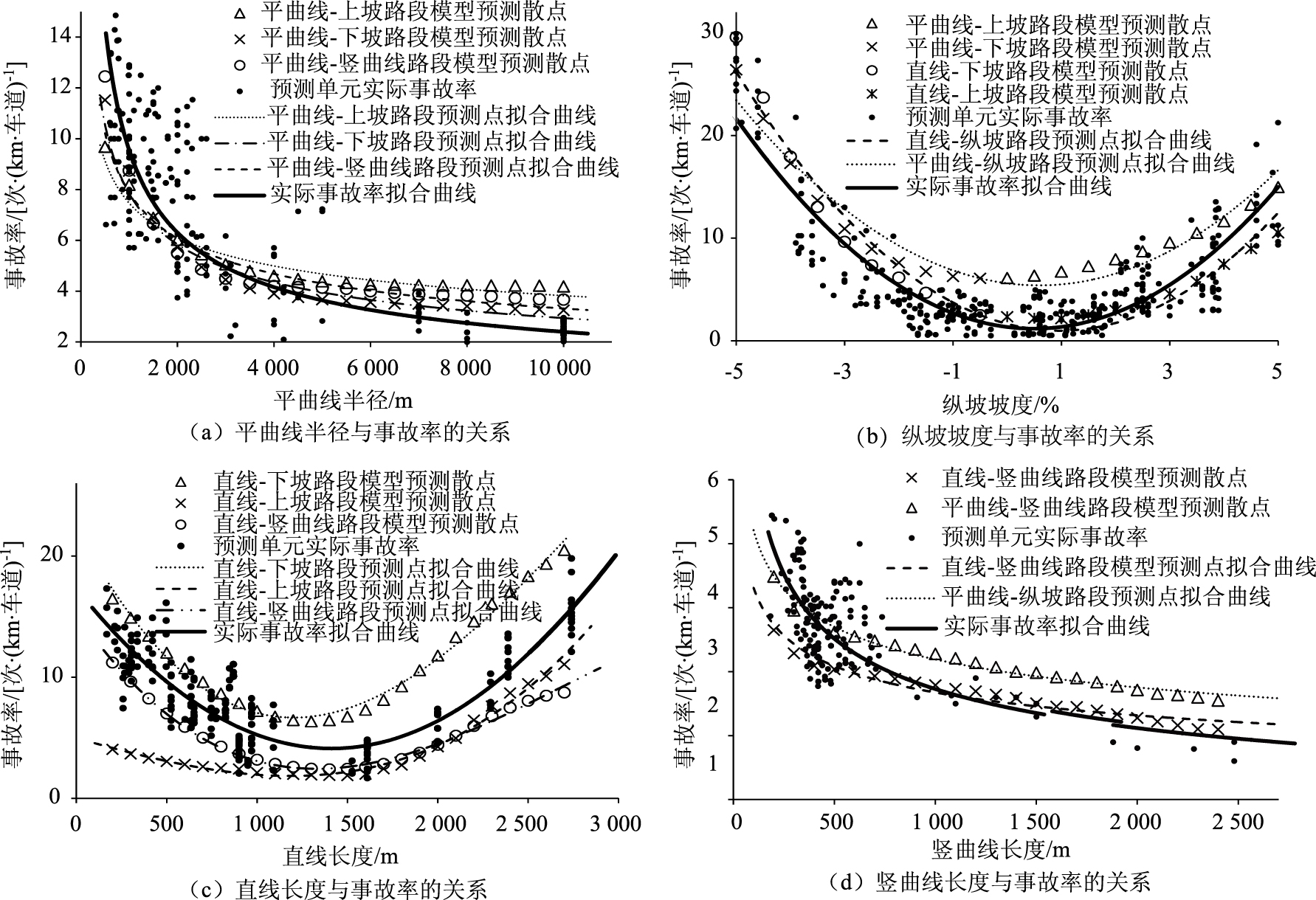
通过敏感性分析所确定的各类路段上平曲线半径与事故率的关系见图 6(a)。显然各类路段上的预测事故率均随平曲线半径的增大而减小,这与基于所有实际数据统计得到的规律(见图 6(a)中的曲线)一致,且符合交通安全中平曲线半径与事故率的基本关系。
|
| 图 6 几何线形指标与事故率的关系 Fig. 6 Relationship among alignment indicators and accident rate |
纵坡路段共有4种,分别为平曲线-上坡路段、平曲线-下坡路段、直线-上坡路段和直线-下坡路段。在敏感性分析时,纵坡坡度最小值取-5%,然后按每级增长0.5%的方式设置纵坡坡度值,直至最大的5%。前两类路段中直线长度取所有直线路段样本均值(此处为1 191.557 m),平曲线半径取所有平曲线路段样本均值(此处为2 137.942 m),其他几何线形指标取理想线形下的指标值。基于敏感性分析所确定的纵坡坡度与事故率的关系见图 6(b),显然,这一关系也符合交通安全中纵坡坡度与事故率的基本关系。
5.3 直线长度的敏感性分析涉及直线长度的路段共有3种:直线-上坡路段、直线-下坡路段和直线-竖曲线路段。直线长度最小值取200 m,然后按每级增加100 m的方式设置直线长度取值。AADT取样本均值,下坡路段坡度、上坡路段坡度、竖曲线长度分别取-2.118%,1.97%,505.767 m(同5.1节),其他几何线形指标取理想线形条件下的指标值。通过敏感性分析确定的直线长度与事故率的关系见图 6(c),显然,不同类型路段上的直线长度与事故率的关系有一定区别(直线-上坡路段和直线-竖曲线路段总体上更安全一些),但总体趋势是一致的。
5.4 竖曲线长度的敏感性分析涉及竖曲线长度的路段只有平曲线-竖曲线和直线-竖曲线两种。竖曲线长度最小取值为200 m,然后按每级增加100 m的方式给出竖曲线长度取值。AADT取均值,直线长度和平曲线半径分别取1 191.557 m 和2 137.942 m(同5.2),其他线形指标取理想线形条件下的指标值。两类路段上竖曲线长度与事故率的关系见图 6(d),显然预测事故率均随竖曲线长度的增大而减小,这与基于所有实际数据统计得到的规律一致,且符合交通安全中竖曲线长度与事故率的基本关系。
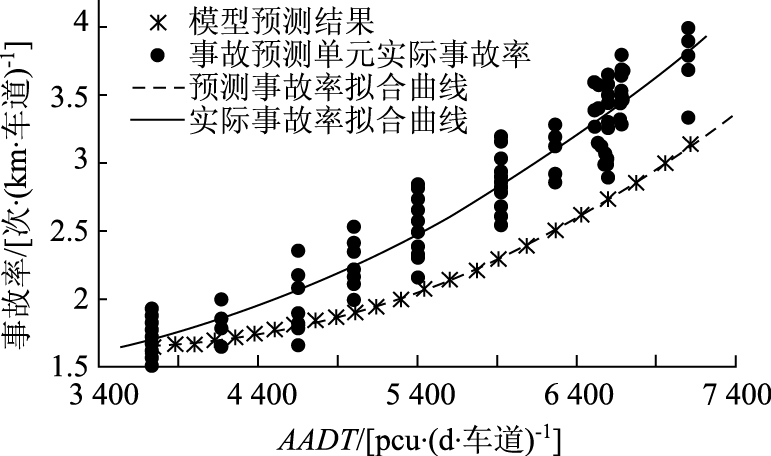
5.5 AADT的敏感性分析进行敏感性分析时,AADT最小取值为3 750 pcu/(d·车道),然后按每级增加125 pcu/(d·车道)的方式设置AADT的取值,其他几何线形指标均取理想线形条件下的指标值。 AADT与事故率的关系见图 7,显然,预测事故率随AADT的增大而增大,这与基于实际数据统计得到的规律一致,且符合AADT与事故率的基本关系。图 7中预测事故率整体低于实际事故率,原因是敏感性分析时将所有几何线形指标均取理想线形条件下的指标值。
|
| 图 7 AADT与事故率关系 Fig. 7 Relationship between AADT and accident rate |
本文得出的平曲线半径、纵坡坡度、直线长度和AADT与事故率的关系曲线与文献[13]中相应规律曲线的一致性较高。
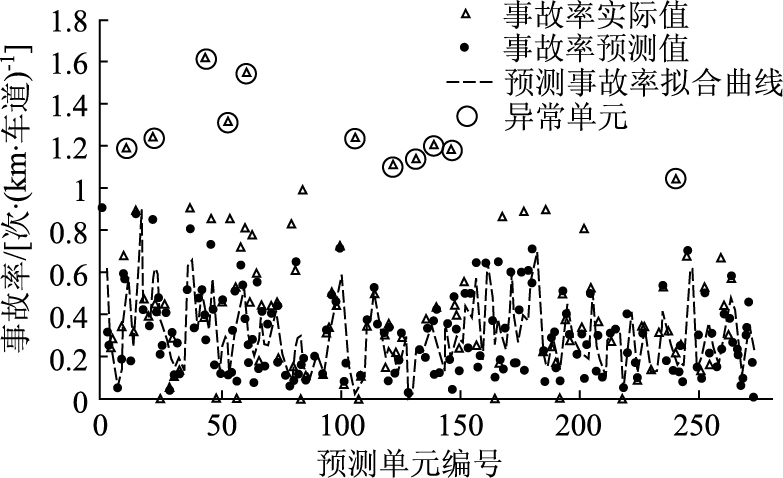
6 模型应用研究应用已标定出的山岭重丘区高速公路交通事故预测模型对沈丹高速公路上的272个事故预测单元进行事故预测,结果见图 8。272个预测单元事故率与实际事故率的平均相对误差绝对值为0.29,相对误差小于0.3的单元有168个,占预测单元总数的62%,通过质量控制法对11个异常单元(图 8中的○单元)进行分析,发现这11个单元均属于事故率较高的事故多发点,因此模型预测结果误差较大,扣除11个异常单元后,预测模型在绝大多数单元上均具有较高的预测精度。
|
| 图 8 沈丹高速公路事故预测单元上的预测事故率与实际事故率 Fig. 8 Predicted and actual accident rates of Shenyang-Dandong expressway accident prediction section |
另外,标定模型得到的京珠高速公路事故预测单元的平均事故率为3.32次/(km·车道),平均AADT为5 854 pcu/(d·车道),而模型应用的沈丹高速公路事故预测单元的平均事故率为0.32次/(km·车道),平均AADT为2 272 pcu/(d·车道),这是两条事故率和交通量相差较大的高速公路,但在沈丹高速公路上应用后仍具有较高的精度,这在一定程度上说明标定的事故预测模型具有一定的可移植性和对山岭重丘区高速公路的通用性。
7 结论由于山岭重丘区高速公路复杂的几何线形条件是诱发交通事故的重要原因,因此尝试开展了基于几何线形指标和AADT的事故预测研究并取得了以下结论:(1)针对事故率与几何线形、交通量之间复杂的非线性关系,建立了Elman神经网络事故预测模型,可对基本路段的事故预测单元进行事故预测。(2)利用粗糙集理论对几何线形指标进行了筛选,简化了模型输入变量,提升了事故预测精度。(3)界定了基于几何线形条件的事故预测单元,利用理想线形条件给出了事故预测单元空值项的赋值方法,解决了模型算法实现的问题。敏感性分析试验表明,本文建立的Elman神经网络事故预测模型在交通安全基本原理上是正确有效的,模型的应用也证明了该模型具有较好的泛化能力和可移植性。
事故预测尤其是微观的事故预测是一个非常复杂的问题,涉及人、车、路、环境以及随机性等很多方面。本文仅从公路几何线形方面建立了事故预测模型,这还远远不够,今后还应逐步考虑并引入其他影响因素,从而不断提高事故预测精度。关于神经网络模型的选择也是一个值得深入研究的问题,本文仅从网络逼近能力方面进行了考虑,还应从神经网络原理上对模型进行进一步的优化和调整。
| [1] | FU R, GUO Y, YUAN W, et al. The Correlation between Gradients of Descending Roads and Accident Rates[J]. Safety Science, 2011(3):416-423. |
| [2] | CHAO W, QUDDUS M A, ISON S G. Predicting Accident Frequency at Their Severity Levels and Its Application in Site Ranking Using a Two-stage Mixed Multivariate Model[J]. |
| [3] | MENG Xiang-hai, GUAN Zhi-qiang, ZHENG Lai. Safety Evaluation of Mountainous Expressway Based on Geometric Alignment Indexes[J]. China Journal of Highway and Transport, 2011, 24(2):103-108. |
| [4] | ANASTASOPOULOS P C, MANNERING F L. A Note on Modeling Vehicle Accident Frequencies with Random-parameters Count Models[J]. |
| [5] | SAWALHA Z, SAYED T. Transferability of Accident Prediction Models[J]. |
| [6] | 孟祥海, 关志强, 郑来. 基于几何线形指标的山区高速公路安全性评价[J]. 中国公路学报, 2011, 24(2):103-108. MENG Xiang-hai, GUAN Zhi-qiang, ZHENG Lai.Safety Evaluation of Mountainous Expressway Based on Geometric Alignment Indexes[J]. China Journal of Highway and Transport, 2011, 24(2):103-108. |
| [7] | WAHLBERG A E A. Some Methodological Deficiencies in Studies on Traffic Accident Predictors[J]. |
| [8] | DOMINGUEZ-LIRA C A, CASTRO M, PARDILLO-MAYORA J M, et al. Adaptation and Calibration of IHSDM for Highway Projects Safety Evaluation in Spain[C]//Proceedings of the 4th International Symposium on Highway Geometric Design. Valencia, Spain:[s. n.], 2010. |
| [9] | MARCHIONNA A, PERCO P, FALCONETTI N. Evaluation of the Applicability of IHSDM Crash Prediction Module on Italian Two-lane Rural Roads[J]. |
| [10] | CHANG L Y. Analysis of Freeway Accident Frequencies:Negative Binomial Regression versus Artificial Neural Network[J]. |
| [11] | 王彪, 段禅伦, 吴昊,等. 粗糙集与模糊集的研究及应用[M].北京:电子工业出版社,2008. WANG Biao, DUAN Chan-lun, WU Hao, et al. Research and Application of Rough Sets and Fuzzy Sets[M]. Beijing:Publishing House of Electronics Industry, 2008. |
| [12] | 侯芹忠. 基于IHSDM框架的高速公路交通事故预测模型[D]. 哈尔滨:哈尔滨工业大学, 2014. HOU Qin-zhong. Expressway Traffic Accident Prediction Model Based on IHSDM Framework[D]. Harbin:Harbin Institute of Technology, 2014. |
| [13] | 孟祥海, 侯芹忠, 史永义. 基于线形指标的山岭重丘区高速公路事故预测模型[J]. 公路交通科技, 2014, 31(8):138-143. MENG Xiang-hai, HOU Qin-zhong, SHI Yong-yi. An Accident Prediction Model for Expressway in Mountainous Hilly Area Based on Alignment Indexes[J]. Journal of Highway and Transportation Research and Development, 2014, 31(8):138-143. |
 2016, Vol. 33
2016, Vol. 33