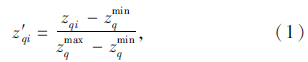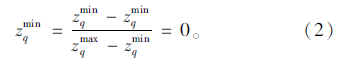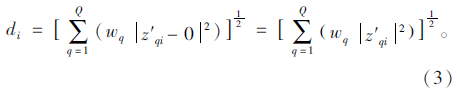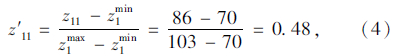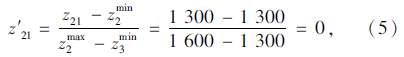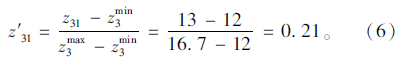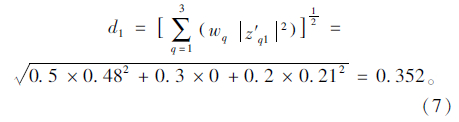扩展功能
文章信息
- 冯树民, 吴海月, 王弟鑫
- FENG Shu-min, WU Hai-yue, WANG Di-xin
- 基于理想点法的多目标最短路求解算法研究
- Study of Multi-objective Shortest Path Algorithm Based on Ideal Point Solution
- 公路交通科技, 2016, Vol. 33 (3): 97-101
- Journal of Highway and Transportation Research and Denelopment, 2016, Vol. 33 (3): 97-101
- 10.3969/j.issn.1002-0268.2016.03.016
-
文章历史
- 收稿日期: 2015-03-19
现实生活中许多问题都属于多目标最优化问题,如工程设计、货物运输、经济规划、金融决策、资源分配等。由于各个目标之间通常存在一些冲突,不可能同时达到最优,因此多目标优化问题一般不存在最优解集,而是一个满意解集,也称为Pareto解集[1, 2]。多目标最短路问题属于特殊的多目标最优化问题,如交通网络上的货物运输问题,它需要同时考虑成本、风险、时间等因素并且尽可能使它们最小。目前多目标最短路求解方法主要包括3类:(1)效用函数法,利用决策者的先验信息确定效用函数,比较常用的方法是线性加权法[3];(2)交互法,利用决策者的先验信息与分析者进行对话,逐步求出最终解[4];(3)产生法,直接求解Pareto解集,然后决策者根据需要找出满意解,主要包括动态规划法、Pareto标记法和Pareto等级法等[5, 6, 7]。对多目标的最短路算法,通常的处理方法是对不同的目标进行线性加权或将某些目标转化为约束条件,但对于线性加权法而言,其权重的确定却很困难。而对于有约束的最短路问题,已经被证明是NP-hard问题[8]。
理想点法[9]的思路是利用决策者的先验信息构造满足所有目标的理想点,然后在约束条件内寻找与该理想点最接近的可行解,该方法在多目标决策及多目标优化中已有广泛应用。郭惠昕等[10]将理想点法用于多目标模糊优化设计,以可行解与正理想点和负理想点的距离构造模糊判决,提出了基于理想点的求解算法。武新宇等[11]应用理想点法对梯级水电站多目标优化模型的非劣解集进行了最优解选择。魏航等[12]在求解双目标最短路问题中定义了双目标最短路的理想点,为多目标最短路问题理想点的构造提供了参考。
本文通过构造多目标最短路问题的理想点,结合k-最短路,提出了基于理想点法的多目标最短路求解算法,这种算法的优势包括:解决具有不同度量单位和相互冲突的多目标决策问题;采用软约束,消除一般多目标函数中存在的“硬约束”(即必须满足的约束条件,这样的硬约束实际上有时候满足不了,因此就产生矛盾方程组,使得问题无解);理想点法的目标函数是求偏差量的最小,而这种偏差是线性距离,计算更加容易。
2 算法分析 2.1 基本模型假设运输路径由Q个目标决定(第q个目标对应的目标值为zq)。在单目标下,对于第q个目标必然存在最短路路径Lq0,其对应的目标值为zqmin,那么zqmin即为第q个目标的理想点,(z1min,z2min,…,zQmin)即为多目标最短路问题的理想点。目标q在路径Li上的目标值为zqi,对于每个目标必然存在目标值最小的路径(即该目标的最短路路径)和目标值最大的路径,因此,目标q的目标值的范围为Xq=[zqmin,zqmax]。
第i条路径Li上所有目标的目标值构成的集合为(z1i,z2i,…,zQi)。 由于各目标值的量纲不同,因此,需要对这些目标值进行归一化处理,消除量纲的影响,同时将所有目标值映射到取值区间0,1。
归一化处理后,目标值变为(z′1i,…,z′qi,…,z′Qi),理想点的目标值变为(0,…,0 ,…,0)。 根据加权欧几里得距离可得到归一化处理后路径Li上的目标值与理想点间的距离di:
式中wq为第q个目标的权重。因此,利用上述方法,多目标最短路问题的目标函数转换为单目标函数mindi。
2.2 算法说明定义:(1)设l1和l2为起点到终点之间的某两条路径,如果目标值z1(l1)≤z1(l2),z2(l1)≤z2(l2),且至少有一个是严格不等式,那么就称l1比l2更有效,有效路径组成的集合即为有效路径集合。(2)设lq*为起点到终点之间考虑第q个目标的最短路,lq*∈Lq*,q=1,2,…,Q,其中Lq*是使得第q个目标对应目标值zq最小的最短路径集合,相应的(minz1(lq*),minz2(lq*),…,zq(lq*),…,minzQ(lq*))为有效解的集合。
实际问题中由于网络复杂,起点到终点的路径不可能一一列举,可以先求解每个目标的最小目标值zqmin,确定目标值上限zqmax,相应地确定每个目标的k-最短路,得到最短路路径集合Ω,集合Ω是多目标问题的有效路径集合。
证明:假设集合Ω中根据第q个目标确定的最短路径lq*不是多目标问题的有效路径,那么肯定存在路径l,使得z1(l)≤minz1(lq*),Z2(l)≤minZ2(lq*),…,zq(l)≤zq(lq*),…,zQ(l)≤minzQ(lq*),且至少有一个是严格不等式,由前提条件可知lq*是使得目标zq达到最小的最短路,则zq(l)=zq(lq*),然而对于其他目标值不可能有zi(l)≤minzi(lq*),i=1,2,…,q-1,q+1,…,Q,与假设矛盾,说明l*q为多目标最短路问题的有效路径,[minz1(lq*),minz2(lq*),…,zq(lq*),…,minzQ(lq*)]为有效解,Ω为有效路径集合。
同时,多目标问题的最优路径肯定是在某个目标的k-最短路中取得。
证明:假设l为多目标问题的最优路径,但l∉Ω,那么对于l而言,必然存在z1min≤z1(l)≤z1max,z2min≤z2(l)≤z2max,…,zQmin≤zQ(l)≤zmaxQ,而对于任一目标值在[zqmin,zqmax]范围内的路径均包括在有效路径集合Ω中,这与l不是集合Ω中的路径的假设矛盾,所以多目标最优路径一定是在某个目标的k-最短路中取得,包含在集合Ω中。说明该方法不会遗漏最优解。
因此可以首先求解各目标对应的k-最短路路径来确定起点到终点间各目标的最短路径集合,即有效路径集合Ω,然后在集合Ω中寻找与理想点距离最小的路径,该路径即为多目标最短路问题的满意解。
3 算法流程在算法分析的基础上,提出基于理想点法的多目标最短路求解算法,具体步骤如下:
(1) 运用Dijkstra算法分别求解各目标的最短路路径Lq0。
(2) 若L10=L20=…=LQ0,则该路径为多目标最短路问题的最优解,算法结束;否则,确定理想点,令k=2,转入步骤(3)。
(3)运用k-最短路算法分别求解各目标对应的k-最短路路径。
(4)根据各目标的k-最短路路径确定起点到终点间的路径集合Ω,并计算集合Ω中所有路径在各目标下对应的目标值zqi,确定各目标对应的取值区间Xq=zqmin,zqmax。
(5)对集合Ω中各条路径上的目标值(z1i,z2i,…,zQi)和理想点(z1min,z2min,…,zQmin)进行归一化处理。
(6)计算归一化处理后的目标值与理想点间的加权欧几里得距离di,确定最小距离所对应的路径。
(7) 令k=k+1,转入步骤(3),若两次所求得的路径相同,则该路径即为多目标最短路问题的满意解,算法结束;否则,继续令k=k+1值,直到前后两次所求得的路径相同为止。
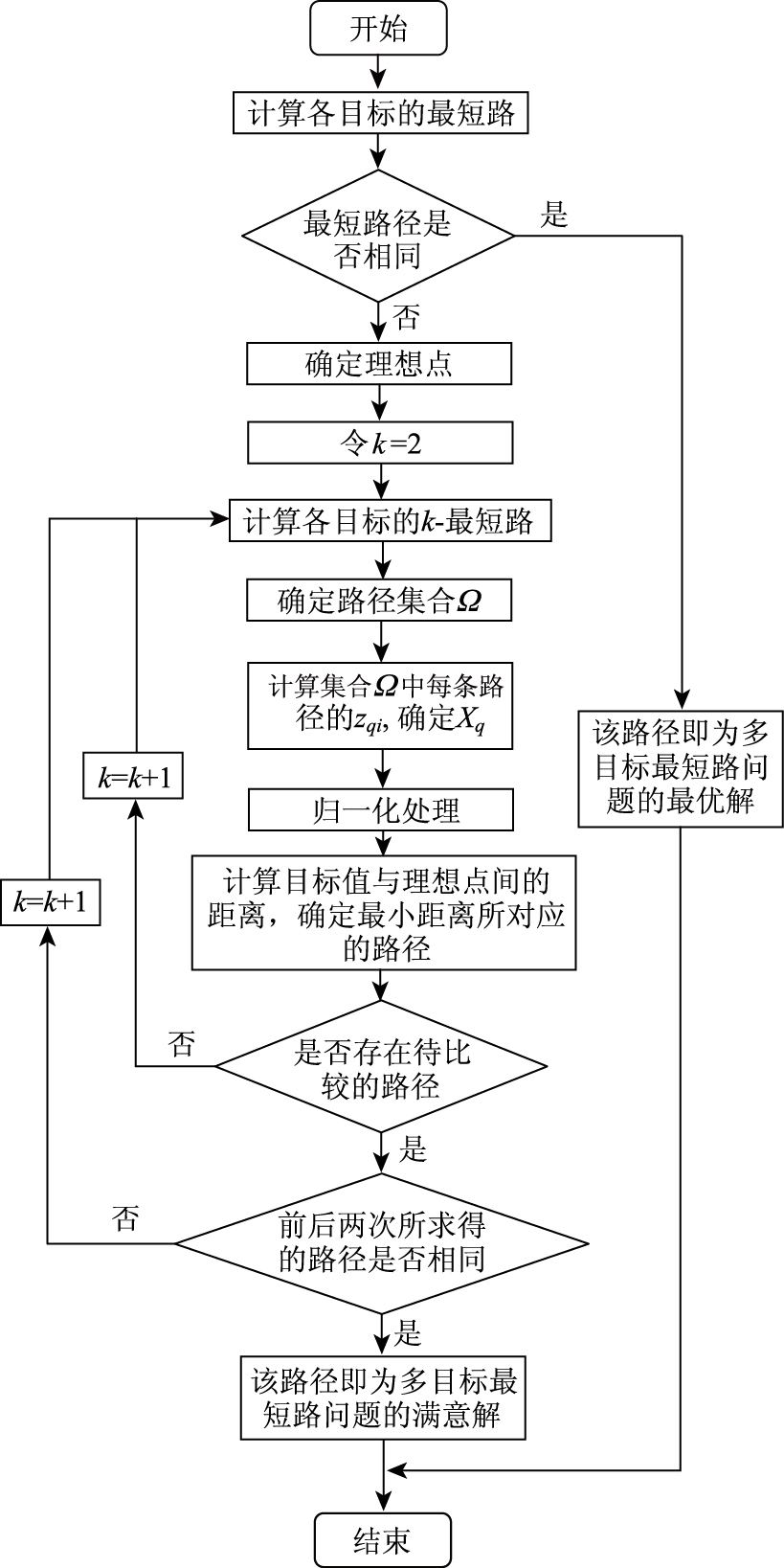
算法流程图如图 1所示。
|
|
图 1 算法流程图 Fig. 1 Flowchart of algorithm |
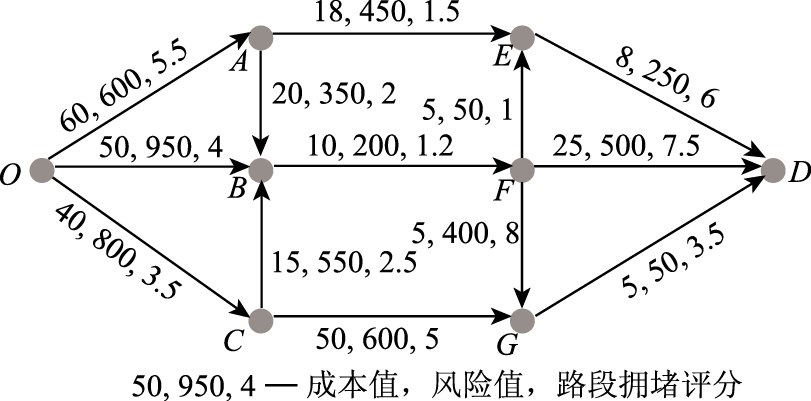
如图 2所示的虚拟运输网络,运输起点为O,终点为D,运输路径选取时考虑成本、
|
| 图 2 运输网络 Fig. 2 Transport network |
风险及路段拥堵程度,其中路段拥堵程度采用路段拥堵评分来度量(路段拥堵评分介于0和10之间,路段拥堵评分越大则路段拥堵越严重)。因此,起点O与终点D间运输路径的选取是一个三目标最短路问题,其中目标1成本最小,对应权重为0.5;目标2风险最小,对应权重为0.3;目标3路段拥堵程度最小,对应权重为0.2。
(1) 求解单目标下各目标的最短路路径
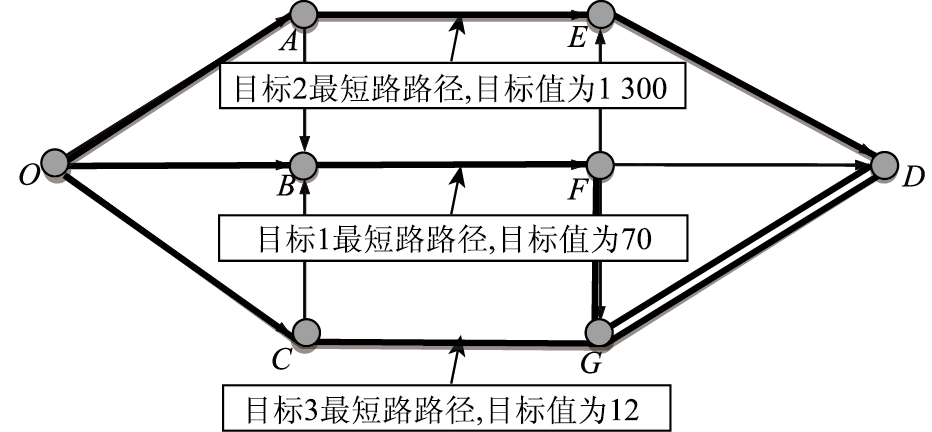
在单目标下,运用Dijkstra算法分别求得各目标的最短路路径及对应的目标值,如图 3所示。
|
| 图 3 各目标最短路路径 Fig. 3 Objective shortest paths |
根据图 3可知,这3个目标的最短路路径均不相同,该多目标最短路问题不存在最优解,只存在满意解。根据各目标最短路路径的目标值可知理想点为(70,1 300,12)。
(2)计算k-最短路路径
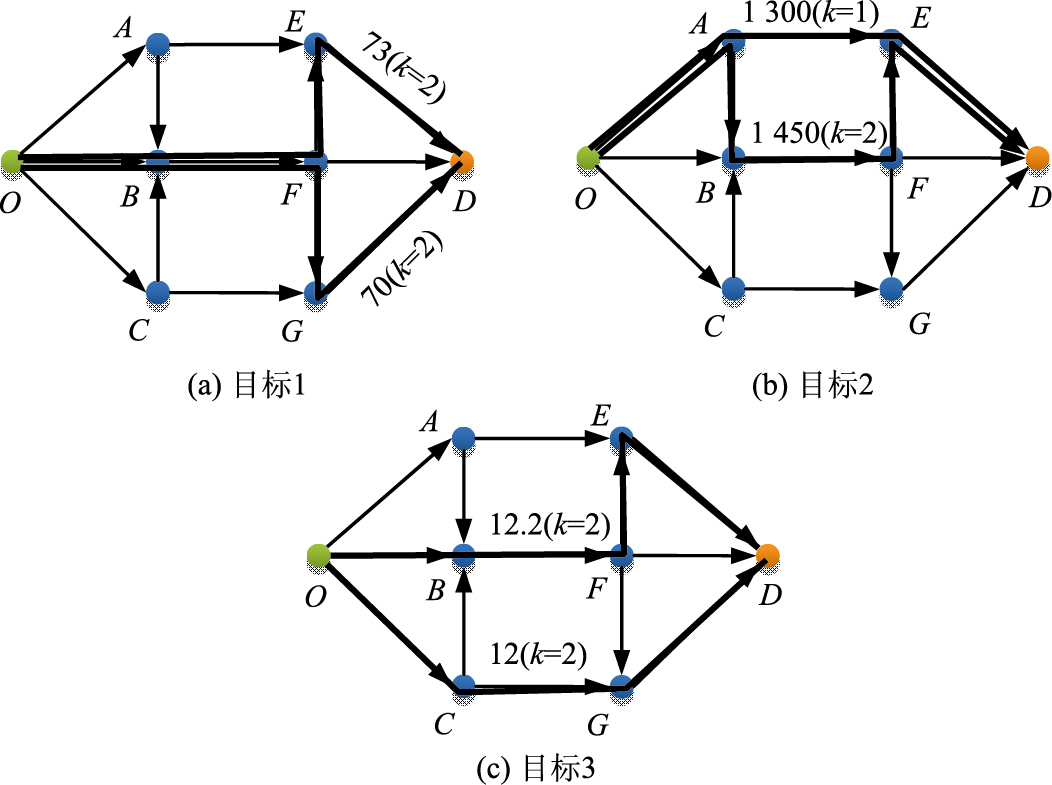
令k=2,在单目标下分别计算各目标的k-最短路路径,计算结果如图 4所示。
|
| 图 4 各目标的k-最短路路径 Fig. 4 Objective k-shortest paths |
(3) 确定最短路径集合Ω
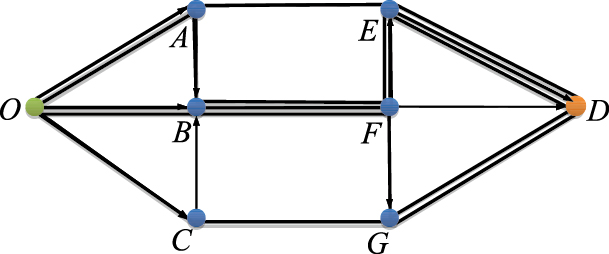
根据图 4中的路径确定最短路径集合Ω,如图 5所示。
|
| 图 5 路径集合Ω中的所有路径 Fig. 5 All the paths in path set Ω |
分别计算集合Ω中每条路径上3个目标的目标值,如表 1所示。
| 目标值 | 路径 | ||||
| OAED | OABFED | OBFED | OBFGD | OCGD | |
| z1 | 86 | 103 | 73 | 70 | 95 |
| z2 | 1 300 | 1 450 | 1 450 | 1 600 | 1 450 |
| z3 | 13 | 15.7 | 12.2 | 16.7 | 12 |
根据表 1可知,3个目标值的取值区间分别为X1=[70,103],X2=[1 300,1 600],X3=[12,16.7]。
(4)归一化处理
根据式(1),对理想点与目标值进行归一化处理。以路径OAED为例,处理后的值为:
(5) 计算目标值与理想点间的距离
根据式(3),计算目标值与理想点间的加权欧几里得距离。以路径OAED为例,计算结果为:
同理,计算其余路径上的目标值与理想点间的加权欧几里得距离,计算结果如表 2所示。根据表 2,最小距离为0.282,对应的路径为OBFED。
| 路径 | OAED | OABFED | OBFED | OBFGD | OCGD |
| di | 0.352 | 0.837 | 0.282 | 0.707 | 0.603 |
(6) 检验
令k=3,按上述步骤再次计算所求得的路径为OBFED,前后两次所求得的路径相同。因此,路径OBFED为该多目标最短路问题的满意解。
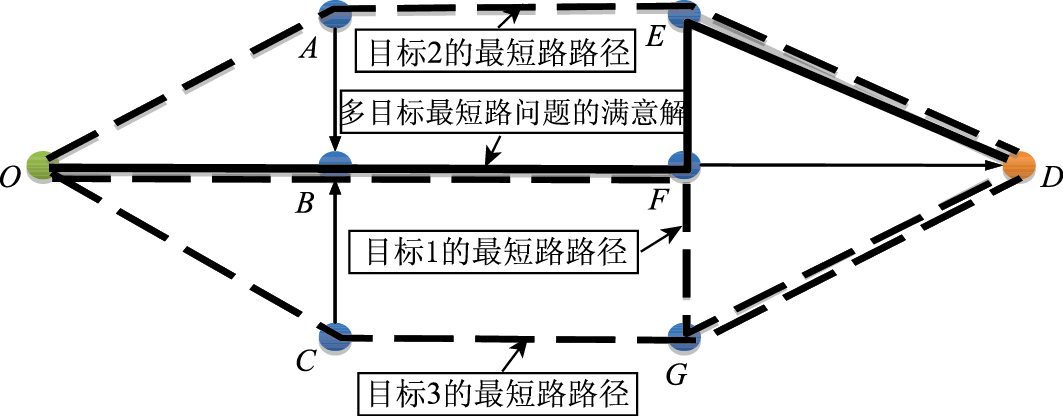
|
| 图 6 多目标最短路满意解 Fig. 6 Satisfactory solution of multi-objective shortest path |
通过运用理想点法对多目标最短路求解进行研究,得到以下结论:
(1)多目标最短路问题的理想点只需通过在单目标下求解各目标的最短路路径便可构造,构造方法简便、直观,有利于理想点法的应用。
(2) 结合k-最短路算法,提出了基于理想点法的多目标最短路求解算法,并给出了算法流程。该算法的核心是在确定理想点的基础上,通过计算k-最短路路径确定起点和终点间的路径集合,然后计算路径集合的每条路径与理想点间的距离,最小距离所对应的路径即为多目标最短路问题的满意解。
(3) 该算法通过判断从各目标的最短路路径是否相同来确定多目标最短路问题是否存在最优解,在此基础上,逐次增加k值并计算k-最短路路径,从这些路径中寻找多目标最短路问题的满意解。该算法计算过程循序渐进,其检验过程防止了潜在的满意解被遗漏。
(4) 该算法简便、易于理解,通过案例分析,验证了算法流程。
| [1] | GRANATA J, GUERRIERO F. The Interactive Analysis of the Multicriteria Shortest Path Problem by the Reference Point Method[J]. |
| [2] | GUERRIERO F, MUSMANNO R. Label Correcting Methods to Solve Multicriteria Shortest Path Problems[J]. |
| [3] | BRUMBAUGH-SMITH J, SHIER D. An Empirical Investigation of Some Bicriterion Shortest Path Algorithms[J]. |
| [4] | GRANATA J, GUERRIERO F. The Interactive Analysis of the Multi-criteria Shortest Path Problem by the Reference Point Method[J]. |
| [5] | SKRIVER A J V, ERSEN K A. A Label Correcting Approach for Solving Bicriterion Shortest Path Problems[J]. |
| [6] | IORI M, MARTELLO S, PRETOLANI D. An Aggregate Label Setting Policy for the Multi-objective Shortest Path Problem[J]. |
| [7] | MACHUCA E, MANDOW L, DE LA CRUZ J L P, et al. A Comparison of Heuristic Best-first Algorithms for Bicriterion Shortest Path Problems[J]. |
| [8] | 郝光, 张殿业, 王东梅. 双目标最短路有效解的快速算法[J]. 公路交通科技, 2007, 24(11):96-99,104. HAO Guang, ZHANG Dian-ye, WANG Dong-mei. A Fast Algorithm for Biobjective Shortest Path[J]. Journal of Highway and Transportation Research and Development, 2007, 24(11):96-99,104. |
| [9] | 范祥莉. 梯级水电站群中长期多目标优化调度方法[D]. 大连:大连理工大学, 2010. FAN Xiang-li. Multi-objective Optimization Scheduling Method of Mid-and-long Term for Cascade Hydropower Station Group[D]. Dalian:Dalian University of Technology, 2010. |
| [10] | 郭惠昕, 张龙庭, 罗佑新,等. 多目标模糊优化设计的理想点法[J]. 机械设计, 2001,18(8):16-18. GUO Hui-xin, ZHANG Long-ting, LUO You-xin, et al. The Ideal Point Method of Multi-target Fuzzy Optimal Design[J]. Journal of Machine Design, 2001,18(8):16-18. |
| [11] | 武新宇, 范祥莉, 程春田,等. 基于灰色关联度与理想点法的梯级水电站多目标优化调度方法[J]. 水力学报, 2012, 43(4):422-428. WU Xin-yu, FAN Xiang-li, CHENG Chun-tian, et al. Multi-objective Optimal Operation Based on Grey Correlation and Ideal Point Method for Cascaded Hydropower Systems[J]. Journal of Hydraulic Engineering, 2012, 43(4):422-428. |
| [12] | 魏航, 蒲云, 李军. 一种求解双目标最短路的方法[J]. 系统工程, 2005, 23(7):113-117. WEI Hang, PU Yun, LI Jun. An Approach to Biobjective Shortest Path[J]. Systems Engineering, 2005, 23(7):113-117. |
 2016, Vol. 33
2016, Vol. 33