扩展功能
文章信息
- 左生荣, 刘杰, 张亚昆, 赵君, 杨吉新
- ZUO Sheng-rong, LIU Jie, ZHANG Ya-kun, ZHAO Jun, YANG Ji-xin
- 规则波浪对不同类型深水桥墩影响的数值分析
- Numerical Analysis of Effect of Regular Waves on Different Types of Deep Water Pier
- 公路交通科技, 2016, Vol. 33 (3): 82-88
- Journal of Highway and Transportation Research and Denelopment, 2016, Vol. 33 (3): 82-88
- 10.3969/j.issn.1002-0268.2016.03.014
-
文章历史
- 收稿日期: 2015-03-01
2. 武汉理工大学 交通学院, 湖北 武汉 430063;
3. 中交泰兴投资建设有限公司, 江苏 泰州 225400
2. School of Transportation, Wuhan University of Technology, Wuhan Hubei 430063, China;
3. CCCC Taixing Investment Construction Co., Ltd., Taizhou Jiangsu 225400, China
近几十年来,随着深水桥墩的建设数量越来越多,规模越来越大,其在施工及使用阶段受到波浪力的影响是关系结构安全与正常运行的关键性问题。国内外很多学者对作用于墩柱结构上的波浪力作了许多实质性的研究,但仍无法全面有效地描述作用于墩柱上复杂的波浪力效应。因此,如何计算作用于墩柱结构上的波浪荷载并提供可靠的理论依据,无论是运用于理论研究和实践设计上,这一直都是国内外学者关注的问题[1]。
由于跨海大桥中下部结构的桥墩长期跟海水接触,受到海洋中的环境荷载影响较大,尤其在波浪或者水流的作用下对桥墩的水平方向受力会有很大的影响,因此波浪荷载应作为深海桥梁下部结构的主要控制外力。而目前对于跨海桥梁的设计规范中并没有对波浪荷载的计算提供明确的公式和方法,由此作为主要控制外力的波浪荷载对桥墩的结构设计成了一个受关注的问题[2]。
1 波浪理论和流固耦合计算方法介绍目前,学术界流行的波浪理论有水波理论(规则波理论)和随机海浪理论(不规则波理论),这两个理论的本质是相互联系、相辅相成的,是海浪对桥墩墩柱结构作用力的研究也是对两个理论的结合[3]。
国内外对波浪力的计算方法非常多,但由于各自的计算原理和适用范围不同,计算结果有较大的差异[4, 5, 6]。我国对波浪要素方法主要采取的公式有:莆田试验站公式、官厅水库公式、鹤地水库公式、安德列扬诺夫公式、SMB法公式等半理论半经验公式,这些不同的公式都是针对某一具体项目测试得到的,因此在其使用上都有一定的适用范围和局限性[7]。为了提高计算精度,在选取计算波浪要素的公式时一定要根据波浪变形、非线性等诸多因素来进行选择。
波浪与桥墩的作用本质上是流固耦合的问题,目前流固耦合问题的计算方法,可以概括为以下两个方面:一类是分别对结构部分和流体有限元法进行离散,并建立流体与固体耦合振动方程式[8],国外学者对于流体为无限域的情况,用有限元法和无限元法结合的方法来进行处理,但由于解的稳定性和衰减长度的不确定性,限制了无限元法的进一步发展。然而,国内不少学者[9, 10]运用流体边界元和结构有限元联合求解流固耦合问题,采用迭代法求解流固耦合振动的特征,用结构在空气的振动模态(干模态)作为初始迭代向量,经过若干次迭代,收敛于湿模态。该法能有效地处理无限域流场流体的水动力计算问题。安泽幸隆[11]等人将结构部分用有限元、流体部分采用边界元离散,同时对流固耦合的交界面模型做出假设,计算结果证明假设是合理的;另一类是结构部分按有限元法进行离散,对流体部分用边界元法离散。其中应用较多的边界元法是在定义域的边界上划分单元,用满足控制议程的函数去逼近边界条件,然后建立流固耦合振动方程式。边界元方法只对边界积分方程离散求解,可大大减少计算量,因此该方法在工程中广泛应用。
其中CFD数值计算方法经过众多实践证明是研究波浪和墩柱结构的一种行之有效的方法[12]。该方法可以运用强大的计算机仿真系统,模拟现实的流体情况,研究其对结构产生的作用。本文基于CFD数值计算方法研究波浪与墩柱结构作用,通过按规律变化的波浪参数来进行数值计算,对结果进行比较分析,找出两者在相互作用过程中的规律,分析对结构安全影响较大的波浪参数。
1.1 波浪与墩柱的相互作用研究运用CFD数值计算方法,选取不同形式的波浪与各种类型深水墩柱的相互作用为研究对象,对计算结果进行分析,得到二者相互作用的规律。
本文选取的对比模型是直径为4.0 m的圆形实体桥墩和边长为4.0 m的方形实体墩,墩高30 m,水深(自由面)20 m,桥墩材料如表 1所示。波浪参数中波长10 m,波高0.4 m,波浪周期为2.53 s,数值方法中海水体密度为 1 030 kg/m3。传播方向从左至右沿x轴正方向。另外文中桥墩模型是非刚体,需要考虑其变形,因此必须设置桥墩的材料参数。另外,本文计算仅考虑水对桥墩的作用,而不考虑桥墩变形对水流的影响,即所谓的单向流固耦合效应。
| 参数 | 墩柱密度ρp/(kg·m-3) | 弹性模量E/Pa | 泊松比γ |
| 数值 | 2 550 | 3.1×1010 | 0.2 |
在有限元理论上,对于计算域的边界条件一般取无穷远处,但受限于计算条件,一般假定对于流体水槽的计算域的选择是结构距入口和出口距离都是5D(D表示圆形墩柱体横截面的直径),本模型为了保证流体的运动得到充分的发展,取值的范围是10D[13]。
运用ANSYS workbench中FLUENT模块进行建模计算,网格划分和数值模拟如图 1、图 2所示。

|
| 图 1 圆形墩柱截面网格示意图 Fig. 1 Gridding of circular pier section |

|
| 图 2 方形墩柱截面网格示意图 Fig. 2 Gridding of square pier section |
图 3、图 4给出了波浪与大直径圆形墩柱和方形墩柱相互作用的的波面变化图,波浪从左至右沿x轴正方向传播。
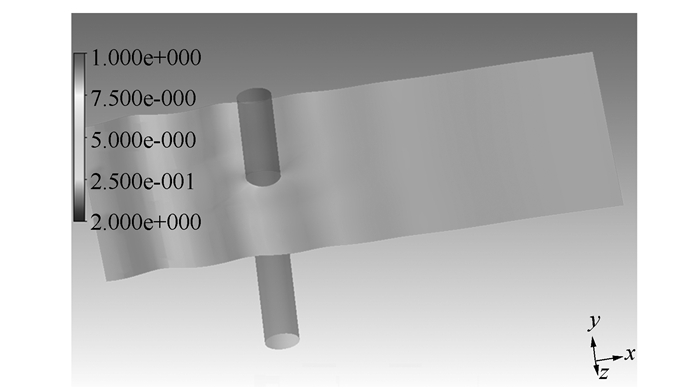
|
| 图 3 波浪与圆形墩柱作用示意图(单位:kN) Fig. 3 Nephogram of wave acting on circular pier (unit:kN) |

|
| 图 4 波浪与方形墩柱作用示意图(单位:kN) Fig. 4 Nephogram of wave acting on square pier (unit:kN) |
通过计算得到如图 5、图 6所示的波浪力时程曲线图。可以得到不同时刻作用在直径4 m圆形墩柱上的波浪力。波峰作用时最大波浪力是23 187.9 N,为正值;波谷作用时的最大波浪力是-23 880 N,为负值。波浪力的周期与波浪周期基本保持一致[14]。波浪作用于方形墩柱时波浪力的振幅整体保持在一个稳定的范围内,波峰作用时最大波浪力正值为25 225 N,波谷作用时最大值达到-27 277.2 N,方形墩柱的波浪力要比圆形墩柱的大。
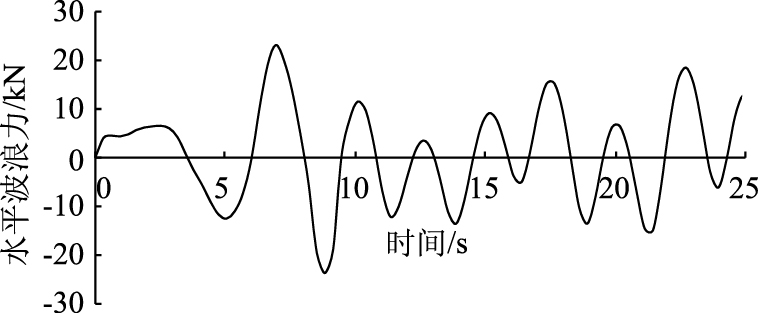
|
| 图 5 圆形墩柱波浪力时程曲线图 Fig. 5 Time history curve of wave force acting on circular pier |

|
| 图 6 方形墩柱波浪力时程曲线图 Fig. 6 Time history curve of wave force acting on square pier |
对于规则线性波浪,波浪参数主要体现在波长和波高上,波长和波高对波浪力大小的影响程度决定波浪参数对墩柱结构设计的重要性。下面分别研究规则波参数中波长和波高的变化对波浪力的影响以及变化规律。
为了分析波长对波浪力的影响,在10 m波长的计算基础上,在其他波浪参数不变的情况下分别把波长变为14 m和18 m。然后分别计算其作用在圆形墩柱上波浪力的大小。
在其他参数不变的情况下,把波高分别增加至0.6 m和0.8 m,然后分别计算其对圆形墩柱产生波浪力的大小。
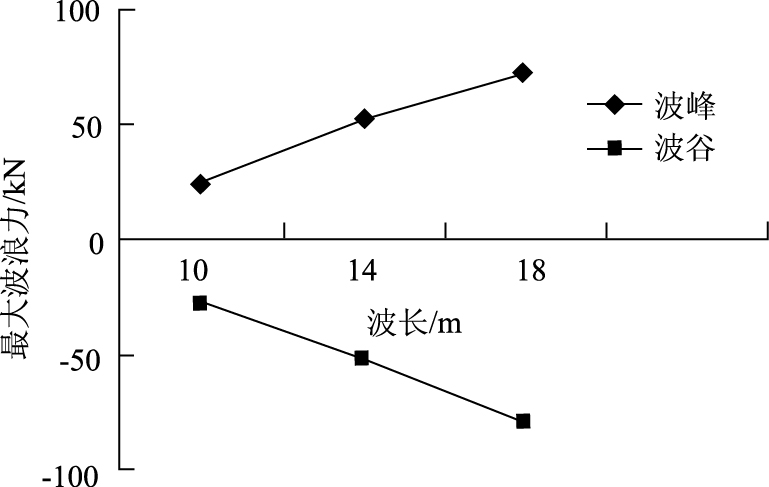
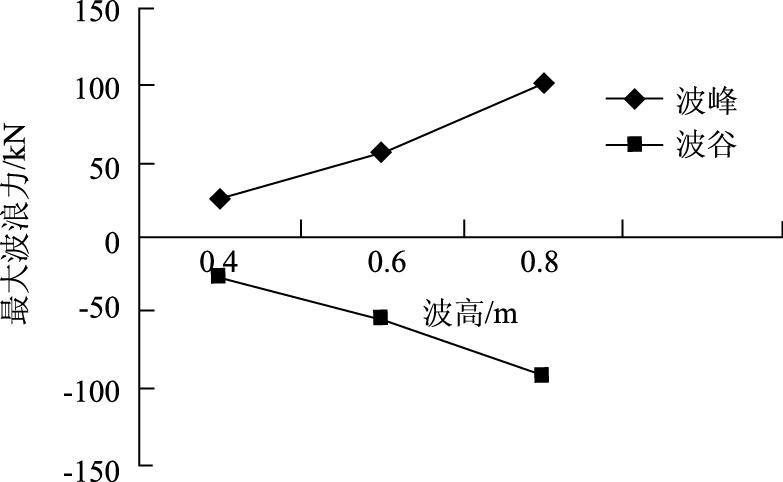
仅选取波高是0.6 m和0.8 m时的波浪力时程曲线图,如图 7、图 8所示。不同波长和波高的波浪力值如表 2及图 9、图 10所示。
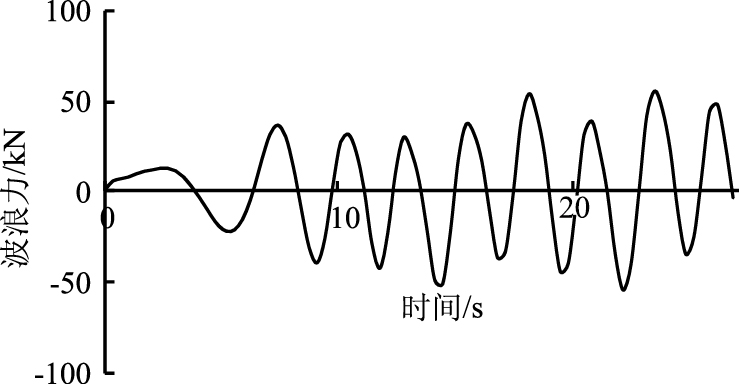
|
| 图 7 波高0.6 m时波浪力的时程曲线图 Fig. 7 Time history curve of wave force when wave height is 0.6 m |
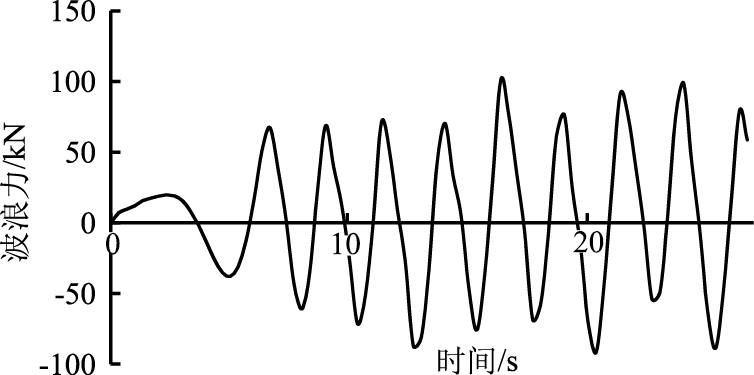
|
| 图 8 波高0.8 m时波浪力时程曲线图 Fig. 8 Time history curve of wave force when wave height is 0.8 m |
| 波浪力/N | 波长/m | 波高/m | ||||
| 10 | 14 | 18 | 0.4 | 0.6 | 0.8 | |
| 波峰 | 23 187.9 | 51 993 | 72 931.6 | 23 187.9 | 55 317.8 | 101 553.6 |
| 波谷 | -23 880 | -51 477.3 | -79 099.2 | -23 880 | -54 663.3 | -90 282 |
|
| 图 9 不同波长对应的最大波浪力图 Fig. 9 Maximum wave forces in different wave lengths |
|
| 图 10 不同波高对应的最大波浪力图 Fig. 10 Maximum wave forces in different wave heights |
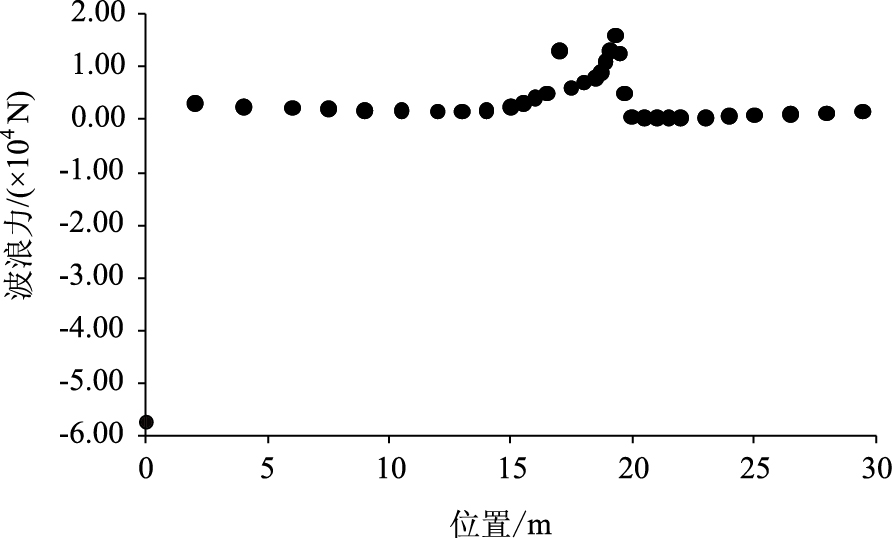
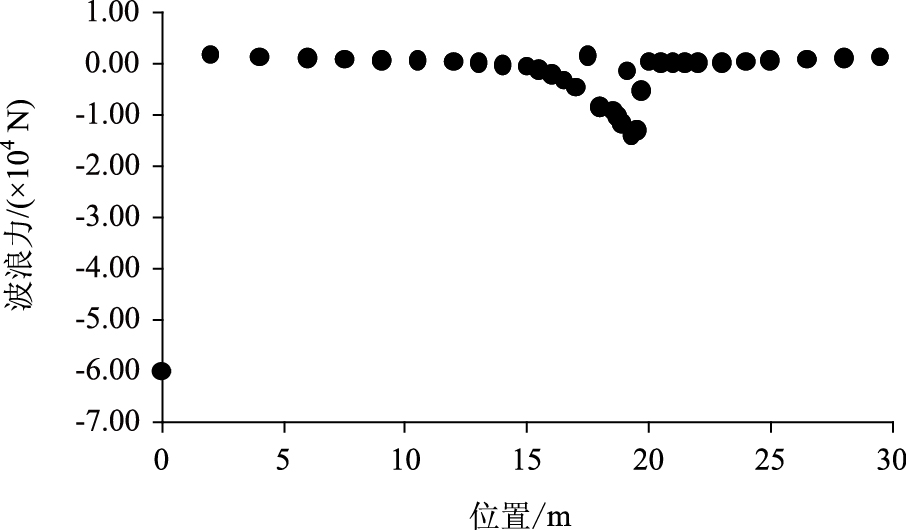
选取墩柱上不同深度对应的波浪力建立如图 11、图 12所示的坐标系,得到波浪力随深度变化的曲线。
|
| 图 11 波峰作用时波浪力随水深的变化图 Fig. 11 Wave force varying with depth under wave peak action |
|
| 图 12 波谷作用时波浪力随水深的变化图 Fig. 12 Wave force varying with depth under wave trough |
从图 11、图 12中可以看出,当波峰作用于墩柱时,在距离墩柱底部越高的迎浪侧处,波浪力越大,在沿墩柱深度往下波浪力逐渐减小至零。
波高和波长变大后,其对波浪力在桥墩深度上的分布规律与之前一致。波浪参数的波长和波高变大后,波浪力在圆形墩柱垂直深度上的影响范围也增大。
4 波浪力作用下的墩柱结构响应分析根据波浪力大小和变化规律,把最大波浪力加载到墩柱结构上,可求得不同形式墩柱结构的应变和应力分布情况,也可得出不同形式墩柱的动力相应。
4.1 波峰作用时大圆形墩柱的响应分析以波长10 m、波高0.4 m的波浪作用时的最大波浪力分别作用于两种形式的桥墩上为例,把波峰的最大作用力加载到圆形墩柱上,如图 13所示。

|
| 图 13 波峰载荷加载图(单位:MPa) Fig. 13 Nephogram of wave peak loading(unit:MPa) |
加载后产生的响应:墩顶的位移和墩底的应力如图 14、图 15所示。

|
| 图 14 波峰作用时圆形墩柱位移云图(单位:mm) Fig. 14 Nephogram of displacement of circular pier under wave peak action(unit:mm) |

|
| 图 15 波峰作用时圆形墩柱应力云图(单位:MPa) Fig. 15 Nephogram of stress of circular pier under wave peak action(unit:MPa) |
把波峰的最大波浪力加载到方形墩柱上,加载后产生的响应,即墩顶的位移和墩底的应力如图 16、 图 17所示。

|
| 图 16 波峰作用时方柱墩位移云图(单位:mm) Fig. 16 Nephogram of displacement of square pier under wave peak action(unit:mm) |

|
| 图 17 波峰作用时方柱应力云图(单位:MPa) Fig. 17 Nephogram of stress of square pier under wave peak action(unit:MPa) |
各种形式的墩柱在规则波(波浪参数是波长10 m,波高是0.4 m)作用下的响应见表 3。
| 结构类型 | 波浪位置 | 墩顶最大位移/mm | 墩底最大应力/MPa |
| 大圆形墩柱 | 波峰 | 0.233 | 0.288 |
| 波谷 | -0.184 | -0.270 | |
| 方形墩柱 | 波峰 | 0.137 | 0.379 |
| 波谷 | -0.147 | -0.381 |
从表 3中可以看出相同波浪条件作用下,相同参数条件的墩柱,外形尺寸越大,在墩顶最大位移越小,在墩底产生的最大应力越大。
4.2 波浪与墩柱作用的模态分析模态分析是研究结构力学特性的一种近代方法,通过分析方法可搞清结构物在某一易变影响的频率范围内各阶主要模态的特性,就可以预言结构在此频段内在外部或内部各种振源作用下产生的实际振动响应。在跨海大桥中的墩柱结构基本上都是大尺度的结构形式,在进行墩柱结构分析时应充分考虑到波浪力作用下结构的动力响应分析[15],从而可以预防和避免结构在这些接近的频率范围内产生较大的响应。
当波浪作用于桥梁墩柱的时候,尽量避免波浪的频率与墩柱的固有频率太接近,易导致共振,长期作用下会引起墩柱的破坏。因此在进行波浪作用下的墩柱结构动力响应分析时,考虑到低阶频率更易发生,首先应进行墩柱的固有频率计算。
结构固有频率大小通过计算可知,大圆形墩柱的固有频率是2.228 8 Hz,方形墩柱的固有频率2.565 4 Hz,而波浪的频率0.395 26 Hz。而且通过计算可知,墩柱尺寸越大,固有频率越高。本文的两个模型中,由于尺寸比较大,固有频率的值相应较高,比波浪的频率高出6~7倍而不易产生共振,结构较安全。
5 结论(1)在相同波浪条件作用下,相同参数条件,不同截面形状的墩柱产生的波浪力的规律是尺寸越大的墩柱产生的波浪力越大。
(2)改变波长和波高两个波浪参数,在一定范围内波长和波高的增长率与波浪力的增长率近似呈线性关系。波浪力在墩柱垂直深度上的分布规律为:从自由液面由上向下沿着墩柱逐渐减小,在距离墩底某个深度后波浪力趋于零,并且随着波长和波高的变大,这个深度的影响范围也相应增大。
(3)相同波浪条件作用下,相同参数条件的墩柱,尺寸越大,在墩顶产生的位移越小,在墩底产生的最大应力越大;墩柱尺寸越大,固有频率越高,与波浪的频率相差较大而不易产生共振,结构相对安全。
| [1] | DEAN R G. Relative Validities of Water Wave Theories[J]. Journal of Waterways, Harbors and Coastal Engineering Division, 1970, 96(1):105-119. |
| [2] | 李玉成,何明.作用于小尺度方柱上的正向波浪力[J].海洋学报,1996,18(3):107-119. LI Yu-cheng, HE Ming. Positive Wave Force Acting on Small-scale Square Column[J]. Acta Oceanologica Sinica,1996,18(3):107-119. |
| [3] | 易家训. 流体力学[M].章克本,等.译:北京:高等教育出版社, 1983. YI Jia-xun. Fluid Mechanics[M]. ZHANG Ke-ben, et al translated. Beijing:Higher Education Press,1983. |
| [4] | 王俊杰.求解声波散射问题的几种方法和大尺度墩柱上的波浪力的数值模型[D].西安:西北大学, 2008. WANG Jun-jie. Several Methods for Solving Acoustic Scattering Problems and Numerical Model of Wave Force Acting on Large Scale Cylinder[D].Xi'an:Northwest University, 2008. |
| [5] | 左其华.方形墩柱上的非线性波浪荷载[J]. 海洋工程,1993,11(1):50-57. ZUO Qi-hua. Nonlinear Wave Loads on Square Cylinder[J]. The Ocean Engineering,1993, 11(1):50-57. |
| [6] | 赵耀南.作用在桩柱上的最大波浪荷载的波浪周期[J].海洋学报,1981,3(3):487-499. ZHAO Yao-nan. Wave-period of Maximum Wave-load Acting on Piles[J]. Acta Oceanologica Sinica, 1981,3(3):487-499. |
| [7] | JTJ213-9,海港水文规范[S]. JTJ213-9,Seaport Hydrology Spectification[S]. |
| [8] | 周锡礽,孙克俐,程庆阳,等.大圆柱壳结构系统的力学机理与数值分析[J].天津大学学报,1996(增1):56-63. ZHOU Xi-reng,SUN Ke-li,CHENG Qing-yang,et al. The Mechanical Mechanism and Numerical Analysis of Large Cylindrical Shell Structure System[J]. Journal of Tianjin University,1996(Sl):56-63. |
| [9] | 沈庆,陈徐均.系泊多浮体系统流固耦合和浮体间耦合动力分析[J].中国造船,2002,43(2):81-84. SHEN Qing,CHEN Xu-jun. Dynamic Analysis of a Mooring Multi-body System Coupled with Fluid and among Bodies[J]. Shipbuiling of China,2002,43(2):81-84. |
| [10] | 沈惠明,赵德有, 罗志雍.流固耦合振动问题的特征值解法[J].大连理工大学学报,1990,30(3):369-372. SHEN Hui-ming, ZHAO De-you, LUO Zhi-yong. Solution to Eigenvalues of Fluid-solid Coupling Vibration Problem[J]. Journal of Dalian University of Technology, 1990, 30(3):369-372. |
| [11] | YASUZAWA Y, SAITO Y. Vibration Analysis of Stiffened Plate in Contact with Water Using Finite Elements and Boundary Elements[J]. Transaction of the West-Japan Society of Naval Architects, 1993,42(86):147-160. |
| [12] | 阎超,于剑.CFD模拟方法的发展成就与展望[J].力学进展,2011,41(5):562-589. YAN Chao, YU Jian. On the Achievements and Prospects for the Methods of Computational Fluid Dynamic[J]. Advances in Mechanics, 2011,41(5):562-589. |
| [13] | 杨吉新,雷凡.水下桥墩结构的振动分析[J].世界桥梁,2009,3(3):40-42. YANG Ji-xin,LEI Fan. Analysis of Vibration of Underwater Bridge Pier Structure[J].World Bridges, 2009,3(3):40-42. |
| [14] | 严开,邹志利,李献丽.不同二阶绕射波浪力理论公式的结果互比[J].工程力学,2013,30(4):31-37. YAN Kai,ZOU Zhi-li,LI Xian-li. The Results Contrast with Different Theory Formula of Second-order Diffraction Wave Force[J].Engineering Mechanics, 2013,30(4):31-37. |
| [15] | 居艮国, 吕风梧,王彬.波浪力作用下钢管桩施工平台随机动力响应分析[J].铁道科学与工程学报,2006,3(5):70-74. JU Gen-guo,LV Feng-wu,WANG Bin. Random Dynamic Response Analysis on Steel-pipe Pile Construction Platform Based on Wave Force[J].Journal of Railway Science and Engineering,2006,3(5):70-74. |
 2016, Vol. 33
2016, Vol. 33
