扩展功能
文章信息
- 杨强, 马如进, 胡晓红
- YANG Qiang, MA Ru-jin, HU Xiao-hong
- 基于抗风性能的高墩连续刚构桥桥墩体系研究
- Study of Pier System of High-rise Pier Continuous Rigid Frame Bridge Based on Wind Resistance Performance
- 公路交通科技, 2016, Vol. 33 (3): 76-81
- Journal of Highway and Transportation Research and Denelopment, 2016, Vol. 33 (3): 76-81
- 10.3969/j.issn.1002-0268.2016.03.013
-
文章历史
- 收稿日期: 2015-03-30
随着我国山区高速公路建设事业的飞速发展,连续刚构桥已成为跨越沟谷最常见的桥型之一。山区地形复杂多变,局部风环境影响因素多,风特性与平原区相比有很大差异[1]。受制于自然地形及设计线型,墩高几十米乃至上百米的刚构桥已屡见不鲜[2]。由于其上部结构悬臂施工长度长、自重大、墩体又常采用薄壁墩,其最大双悬臂状态的振动频率往往较低[3],加之西部山区地形风荷载比较复杂,因而风致振动响应就成为桥梁设计、施工者们十分关心的问题[4]。高墩大跨连续刚构桥本身受力复杂,施工状态多变,有必要对其采用超高墩结构形式所引起的受力、变形及稳定性等力学行为进行分析,以保证施工安全性及线形、受力符合设计要求[5]。
对于分离式的连续刚构桥,为减小横桥向桥墩计算长度及保证横桥向结构的稳定性,通常会在左、右幅桥墩之间设置系梁。双肢薄壁桥墩之间增设墩间系梁可增强双薄壁墩连续刚构桥的稳定性和减小墩顶纵向位移[6, 7, 8, 9]。但设置系梁后,结构地震响应呈增大趋势,而墩中设横梁是横梁设置位置中的最佳方案[2]。横梁的数量和位置以及墩高不仅关系到结构本身的动力特性,也对结构静力性能和抗风性能影响很大,一定程度上还影响桥梁施工设计的便捷经济。为此,本文以西部山区某预应力连续刚构桥作为研究对象,通过分离式桥墩间横系梁设置以及墩高参数分析,进行桥梁动力特性、静风作用下的静位移及脉动风作用下抖振响应研究。
1 结构模型西部山区某连续刚构桥跨径布置为120 m+3×175 m+96 m,桥墩采用钢筋混凝土空心墩。两主墩高度分别为143 m和148 m。利用有限元分析软件建立有限元模型,对该模型进行结构动力特性分析。其中主梁与墩柱采用三维空间梁单元模拟,基础、承台未加以考虑,整个桥梁的上部结构在承台处固结。
在原模型两横梁的基础上共选取如下7种体系:(a)不设墩横梁;(b)远墩顶位置设一道墩横梁(距墩顶68.5 m);(c)近墩顶位置设一道墩横梁(距墩顶1 m);(d)原模型,即两横梁状态;(e)三道墩横梁:在原模型上再加设一道墩横梁,加设在原结构中间墩横梁下侧中点处;(f)三道墩横梁:在原模型上再加设一道墩横梁,加设在原结构两个墩横梁中间处。(g)四道墩横梁:在原模型上再加设两道墩横梁,分别加设在原模型两个墩横梁中间处、原模型中间墩横梁下侧中点处。不同桥墩体系时的成桥状态有限元模型如图 1所示。

|
| 图 1 不同桥墩体系的有限元模型 Fig. 1 FE models of different bridge pier systems |
由于不设墩横梁时两幅桥无横向连接,故两幅桥可作为单幅桥进行比较。动力特性不仅对成桥状态进行了参数分析,同时也针对施工最不利悬臂状态进行了比较,通过分析得出在结构主要振型对应的振动频率随墩横梁数量和位置的变化规律分别如图 2和图 3所示。

|
| 图 2 成桥状态结构频率 Fig. 2 Frequency of bridge in finished state |

|
| 图 3 施工最大悬臂状态结构频率 Fig. 3 Frequency of bridge in longest cantilevered state |
图 2为成桥状态各体系条件下前七阶结构频率分析结果。由图可知,主梁竖弯振型与桥墩横桥向连接体系基本无关,这也符合连续刚构桥的基本结构特点。然而,上部主梁结构侧弯振型受连接体系的影响较大。主梁一阶侧弯振型频率在体系a横桥向无连接时的0.15 Hz可提高到体系g横桥向四横梁连接时的0.279 Hz。同样,主梁二阶侧弯振型频率也由体系a时的0.248 Hz提高到体系g时的0.32 Hz。其中值得注意的是,当主梁高度处不设横梁即体系b时,高阶侧弯振型频率明显低于其他体系。可见,主梁高度处设置横梁对提高横桥向刚度有明显作用。图 3给出了主梁施工最大悬臂状态下前六阶振型分析结果,与成桥状态类似,桥墩扭转、顺桥向弯曲振型及主梁竖弯振型受横桥向连接体系影响很小。桥墩横桥向振动受连接体系影响很大,振动频率可由体系a的0.124 Hz提高到体系g时的0.293 Hz。
综上比较可见,对于连续刚构桥侧向刚度而言,双幅桥横桥向连接体系对横桥向刚度影响较大,在进行初步结构选型时,可基于此进行结构体系优化比较。
2.2 墩高对结构动力特性的影响为研究的方便,这里仅取体系a即设置一道横隔梁进行研究,并取墩高变化从30 m到150 m,间隔10 m。由于施工最大悬臂状态是桥梁最不利的结构状态,这里重点针对不同墩高下最大悬臂施工状态的结构动力特性开展研究。图 4给出了结构主要频率随墩高的变化规律。

|
| 图 4 主梁施工最大悬臂状态前五阶频率随墩高变化规律 Fig. 4 Change law of first five-order frequencies of main beam in longest cantilevered state |
由图 4可见,随着墩高的增加,桥梁各主要振型对应的振动频率都在下降;墩高的变化引起桥墩侧弯、一阶扭转和一阶顺桥向振动频率的明显变化,墩高30 m和150 m时的桥墩侧弯频率为0.925 Hz和0.223 Hz,频率降低约4.1倍;一阶扭转频率为0.481 Hz和0.209 Hz,频率降低约2.3倍;一阶顺桥向振动频率为0.497 Hz和0.149 Hz,频率降低约3.3倍。可见墩高变化对桥梁的横向刚度、扭转刚度和顺桥向刚度影响较大,墩高越高,刚度越小,其中尤其对桥墩横向影响最大。而主梁竖弯振型振动频率变化较小,150 m时的频率与墩高30 m时相差不大,说明墩高变化对主梁竖弯影响较小。
综上来看,墩高的变化对桥墩自身的一阶振动频率影响很大,而对主梁的振动影响较小。桥墩一阶扭转和一阶顺桥向振动的振型较早出现,说明施工悬臂阶段桥墩自身的振动对桥梁起控制作用,而主梁振动对桥梁影响较小。
3 静风荷载响应比较研究 3.1 桥墩横桥向体系对静风荷载效应的影响针对不同桥墩横桥向体系的抗风性能研究,选取设计基准风速Vd=31.6 m/s。根据《公路桥梁抗风设计规范》[10],在横桥向风作用下主梁或桥塔单位长度上的横向静阵风荷载为:

通过对不同结构体系成桥状态和主梁施工最大悬臂状态进行分析,图 5给出了横桥向静风荷载作用下成桥状态桥梁跨中和墩顶部横向位移与桥墩横桥向结构体系的关系。由图可见,在横桥向静风荷载作用下,桥墩横向连接体系对中跨跨中和中墩顶部横向位移影响较大,而对边跨跨中和边墩顶部以及背风侧影响较小。中跨跨中和中墩顶部迎风侧横向位移随墩横梁数量增加和位置的提高而显著减少,这与动力特性分析时墩横梁可以显著提高横桥向刚度是一致的。体系a,b背风侧位移比体系c~g横向位移还小,说明不设墩横梁或位置较低时两幅桥协同性不好,受力性能不佳。与不设墩横梁相比,横梁能有效减少迎背风侧横向位移之比,提高桥梁横向整体刚度,使两幅桥协同受力。

|
| 图 5 成桥状态关键节点横桥向位移 Fig. 5 Lateral displacement of key nodes in finished state |
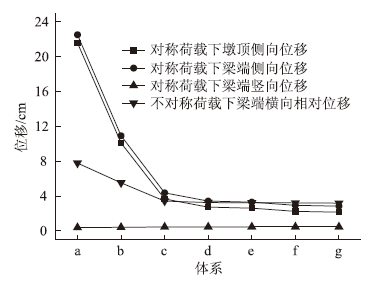
图 6给出了主梁施工最大悬臂状态关键节点横向和竖向位移与桥墩横桥向结构体系的关系。由于对背风侧位移影响较小,故只讨论迎风侧位移。与成桥状态类似,桥墩横向连接体系对横向位移影响较大,而对竖向位移影响很小。墩横梁数量越多、位置越高,横向刚度越大,横桥向位移越小。同时桥墩横向连接体系能够有效减小不对称横向风荷载作用下主梁的扭转,说明桥墩横向连接体系还可以提高扭转刚度。同时可以看出,两横梁体系d与四横梁体系g位移相差不大,说明两横梁体系d是比较合理的体系。
|
| 图 6 主梁施工最大悬臂状态关键节点位移 Fig. 6 Displacement of key nodes in longest cantilevered state |
对主梁施工最大悬臂状态不同结构体系的静风荷载效应进行分析,得到关键节点位移随墩高的变化规律如图 7所示,可知在静风荷载作用下,墩高对梁端竖向位移的影响很小。在顺桥向静风荷载作用下,桥梁顺桥向位移随墩高的增加有明显增大的趋势,墩顶顺向位移在墩高30 m时为0.053 cm,墩高150 m时为3.255 cm,是墩高30 m时的61.4倍。横桥向静风荷载作用随着墩高的增加,梁端及墩顶部横向位移明显增大,墩高对梁端及墩顶横向位移影响比较明显,墩顶横向位移在墩高30 m时为0.106 cm,墩高150 m时为3.855 cm,是墩高30 m时的36.4倍,悬臂端部横向位移在墩高30 m时为0.676 cm,墩高150 m时为4.56 cm,是墩高30 m时的6.7倍。同时在不对称荷载作用下梁端横向相对位移随着墩高增加而增大,且趋势逐渐减缓,说明墩高不仅对横向刚度、竖向刚度有影响,对扭转刚度也有影响,墩高越大,扭转刚度越小。

|
| 图 7 主梁施工最大悬臂状态关键节点位移随墩高的变化规律 Fig. 7 Law of displacement of key nodes of main beam varying with pier height in longest cantilevered state |
基于随机抖振分析理论,采用时域分析法,利用谐波合成法模拟脉动风场,基于抖振力风荷载模型,开展不同结构下的抖振响应分析。分析采用时间步长为0.01 s,结构阻尼比为0.02。应用MATLAB软件对脉动风速进行模拟,得出脉动风速时程曲线,为风致振动分析提供数据[11, 12]。
抖振响应分析中结构受到的风荷载包括静风力、抖振力。由于混凝土连续刚构桥刚度较大,可不考虑自激力作用,抖振力采用Davenport抖振力模型如下[13, 14, 15]:

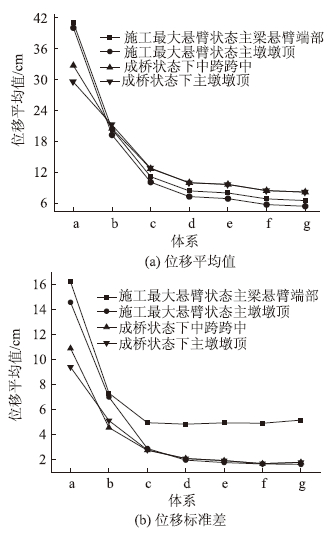
由于墩横梁数量和位置对顺桥向位移影响不大,故只取横桥向位移来研究。图 8给出了成桥状态和施工最大悬臂状态关键节点抖振位移响应与桥墩不同连接体系的关系,其中8(a)和8(b)分别为抖振位移响应的平均值和标准差。从图中可以看出,随着墩横梁数量的增加和位置的提高,桥梁结构横向刚度提高,成桥状态和主梁最大施工悬臂状态下中跨跨中和主墩墩顶抖振位移响应平均值和标准差均随之减小。图 8(a)中施工最大悬臂状态时主梁悬臂端部位移平均值由体系a时的41.04 cm下降到体系g时的6.57 cm,下降为体系a的6.25倍,但体系d时为8.45 cm,与体系g相差不大;图 8(b)中施工最大悬臂状态时主梁悬臂端部位移标准差由体系a时的16.24 cm下降到体系d时的4.86 cm,下降为体系a的3.34倍,而体系d到体系g基本不变,性能基本接近,说明设置一定的墩横梁对改善结构抖振响应有明显的效果,但墩横梁数量增加到一定程度后,这种改善效果明显减小。其他关键节点类似。由此得出结论,从抖振响应角度看,体系d即设置两道墩横梁,为高墩连续刚构桥中桥墩连接体系最优的选择。
|
| 图 8 关键节点抖振位移响应与桥墩连接体系的关系 Fig. 8 Relationship between buffeting displacement response of key nodes and bridge pier connection system |
通过对施工最大悬臂状态下不同墩高结构抖振响应的研究,得到抖振位移响应随墩高的变化规律如图 9所示,从图 9(a)中可以看出,主梁悬臂端部和主墩墩顶抖振位移响应平均值随着墩高的增加而增加,且主梁悬臂端部位移响应大于主墩墩顶;而图 9(b)中主墩墩顶抖振位移响应标准差随墩高增加而增加,且明显小于主梁悬臂端部,主梁悬臂端部抖振位移响应标准差先随墩高增加而增加,在墩高为110 m左右时达到最大,然后基本维持在一定范围,略有减小的趋势。分析原因,主要由于桥墩扭转模态下结构基频在墩高超过110 m时逐渐低于0.22 Hz,此时脉动风谱能量基本保持在高位恒定水平,因此在抖振激励下,墩高持续增加并不会引起振动幅值的大幅增加。

|
| 图 9 施工最大悬臂状态关键节点抖振位移响应与墩高的关系 Fig. 9 Relationship between buffeting displacement response of key nodes and pier height |
通过分离式桥墩间横系梁设置以及墩高参数分析,对桥梁动力特性、静风作用下的静位移及脉动风作用下抖振响应研究可得:
(1)桥墩横梁的数量和位置对桥墩低阶侧弯频率影响较大,而对桥墩扭转、顺桥向弯曲振型及主梁竖弯振型影响较小。同时,墩高的变化对桥墩自身的一阶振动频率影响很大,而对主梁的振动影响较小。桥墩一阶扭转和一阶顺桥向振动的振型较早出现,说明施工悬臂阶段桥墩自身的振动对桥梁起控制作用,而主梁振动对桥梁影响较小。
(2)在横桥向静风荷载作用下,桥墩横梁的数量、位置对桥梁横向位移影响较大,墩横梁数量越多及位置越高,横桥向位移越小,随墩高的增加,墩顶横向位移明显增大,但两横梁体系d与四横梁体系g位移相差不大,说明两横梁体系d是比较合理的体系。同时,设置一定的墩横梁对改善结构抖振响应有明显的效果,但墩横梁数量增加到一定程度后,这种改善效果明显减小。基于抗风性能角度,体系d即设置两道墩横梁,为高墩连续刚构桥桥墩连接体系最优的选择。
(3)在横桥向风荷载作用下,墩高对梁端及墩顶横向位移影响明显,随着墩高的增加,梁端及墩顶横向位移明显增大,同时在顺桥向风荷载作用下,桥梁顺桥向静风位移随墩高增加有明显增大的趋势。墩顶抖振位移响应标准差随墩高增加而增加,且明显小于主梁悬臂端部,主梁悬臂端部抖振位移响应标准差先随墩高增加而增加,在墩高为110 m左右时达到最大,然后基本维持在一定范围,略有减小的趋势。
| [1] | 叶征伟. 山区高墩大跨连续刚构桥风环境及风荷载研究[D]. 杭州:浙江大学,2012. YE Zheng-wei. Study on Wind-environment and Wind Loads of Long-span Continuous Rigid Frame Bridge with Tall Piers in Mountainous areas[D]. Hangzhou:Zhejiang University, 2012. |
| [2] | 尚维波, 张春宁. 高墩刚构桥系梁抗震分析[J]. 长安大学学报:自然科学版,2012,32(1):62-65. SHANG Wei-bo, ZHANG Chun-ning. Seismic Analysis of Tie Beam of Rigid Frame Bridge with High Pier[J]. Journal of Chang'an University:Natural Science Edition, 2012,32(1):62-65. |
| [3] | 郑史雄, 廖海黎, 周述华. 大跨度刚构桥悬臂施工状态的抗风性能研究[J]. 西南交通大学学报,2001,36(1):8-11. ZHENG Shi-xiong, LIAO Hai-li, ZHOU Shu-hua. Study on Wind Resisting Performance of Long-span Rigid Frame Bridge in Its Cantilever Construction Stage[J]. Journal of Southwest Jiaotong University, 2001,36(1):8-11. |
| [4] | 刘榕, 张志田, 刘海波. 大跨度分离式高墩连续刚构抗风性能研究[J]. 中外公路,2012,32(6):160-163. LIU Rong, ZHANG Zhi-tian, LIU Hai-bo. Study on Wind Resistance Performance of Long-span Separated High-rise Continuous Rigid Frame Bridge[J]. Journal of China and Foreign Highway, 2012, 32(6):160-163. |
| [5] | 周维. 大跨度预应力混凝土连续刚构桥超高墩行为分析[D]. 成都:西南交通大学, 2008. ZHOU Wei. Analysis on Mechanic Behaviors of Super High-piers of Long-span PC Continuous Rigid Frame Bridge[D].Chengdu:Southwest Jiaotong University, 2008. |
| [6] | 王淳. 高墩大跨连续刚构桥动静力计算与稳定性研究[D]. 武汉:武汉理工大学, 2006. WANG Chun. Static & Kinetic Computation and Stability Research of Long-span Continuous Rigid Frame Bridge with High-pier[D]. Wuhan:Wuhan University of Technology, 2006. |
| [7] | 张昌伟. 雷堡坳大桥高墩稳定性分析[J]. 交通科技,2012,2(2):25-28. ZHANG Chang-wei. Stability Analysis of Leibaoao Bridge With High Pier[J]. Transportation Science and Technology, 2012, 2(2):25-28. |
| [8] | 马玉全,王景奇.墩间系梁对双肢薄壁高墩连续刚构稳定性的影响[J]. 广东公路交通,2013,7(2):27-29. MA Yu-quan, WANG Jing-qi. Influence to Stability of Continous Rigid Structure of Double-shaft and Thin-wall High-rise Pier by Collar Tie Beams[J]. Guangdong Highway Communications, 2013, 7(2):27-29. |
| [9] | 王应槐. 高墩大跨连续刚构桥静动力及稳定性研究[D]. 长沙:长沙理工大学, 2009. WANG Ying-huai. Static & Dynamic Analysis and Stability Research of Long-span Continuous Rigid Frame Bridge with High Pier[D]. Changsha:Changsha University of Science and Technology, 2009. |
| [10] | JTG/T D60-01-2004, 公路桥梁抗风设计规范[S]. JTG/T D60-01-2004, Wind-resistant Design Specification for Highway Bridges[S]. |
| [11] | 胡登峰.高墩大跨连续刚构桥风致响应研究[D]. 昆明:云南大学, 2014. HU Deng-feng. Wind Response Analysis of Long-span Continuous Rigid Frame Bridge with High Pier[D]. Kunming:Yunnan University, 2014. |
| [12] | 韩万水,陈艾荣. 考虑桥塔风场效应的斜拉桥抖振时域分析[J]. 工程力学, 2007,24(1):123-128. HAN Wan-shui, CHEN Ai-rong. Time-domain Buffeting Analysis of Cable-stayed Bridge Considering Pylon Wind Field[J]. Engineering Mechanics, 2007, 24(1):123-128. |
| [13] | DAVENPORT A G. Buffeting of a Suspension Bridge by Storm Winds[J]. Journal of Structural Division, 1962, 88(3):233-268. |
| [14] | 陈政清.桥梁风工程[M]. 北京:人民交通出版社,2005:100-103 CHEN Zheng-qing. Wind Engineering of Bridge[M].Beijing:China Communications Press, 2005:100-103. |
| [15] | 项海帆, 葛耀君, 朱乐东, 等. 现代桥梁抗风理论与实践[M].北京:人民交通出版社, 2005. XIANG Hai-fan, GE Yao-jun, ZHU Le-dong, et al. Modern Theory and Practice on Bridge Wind Resistance[M]. Beijing:China Communications Press, 2005. |
 2016, Vol. 33
2016, Vol. 33
