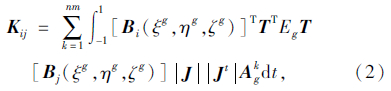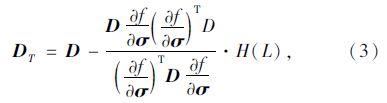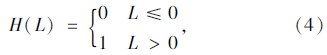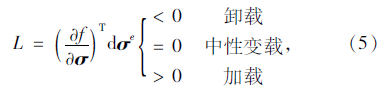扩展功能
文章信息
- 景强
- JING Qiang
- 基于实体退化虚拟层合单元预制桥墩承载力分析
- Analysis of Capacity of Prefabricated Bridge Pier Based on Degenerated Solid Virtual Laminated Elements
- 公路交通科技, 2016, Vol. 33 (3): 71-75
- Journal of Highway and Transportation Research and Denelopment, 2016, Vol. 33 (3): 71-75
- 10.3969/j.issn.1002-0268.2016.03.012
-
文章历史
- 收稿日期: 2015-06-18
港珠澳大桥跨越珠江口伶仃洋海域是连接香港、珠海市和澳门的重要大型跨海枢纽,其主体工程范围自粤港分界线至珠澳口岸之间区段,总长29.6 km,其中桥梁长约22.9 km,沉管隧道长5.99 km(不含桥隧过渡段),为实现桥隧转换设置两个长度各为625 m的隧道人工岛[1, 2]。
由于该项目受阻水率限制,将承台全部埋于海床,同时为能确保混凝土施工质量,避免做混凝土封底,减少开挖量,减少现场工作量,缩短工期,减小对环境影响,施工风险小,提出对下部结构进行预制的设想,即桥梁下部结构工程采用了“预制埋床式墩台”方案[3]。由于首次采用埋床法预制墩台及钢管复合桩技术,无相关规范及经验可供参考,设计、施工技术难度均较大。该技术施工过程中体系转换频繁、受力状态复杂,亟需通过采用先进的数值模拟分析技术,对港珠澳大桥预制埋床式墩台桥墩的安全性和承载力进行评估。
由于桥墩是典型的实体结构,采用传统有限元方法进行承载力分析需要划分大量的单元,进行非线性分析时由于多步迭代计算效率非常低。基于此,本文针对港珠澳大桥采用的“预制埋床式墩台”方案,采用实体退化虚拟层合单元拼装预制墩身进行承载力分析,进一步明确掌握预制桥墩墩身的工作性能及承载力特征,评估桥梁下部结构施工过程的受力特点及结构的安全性,为完善和优化设计方案提供依据。
1 实体退化单元理论传统有限单元如实体等参元或板壳单元模拟实际桥梁结构需采用较多的单元数量,效率较低。与传统有限单元不同,实体退化单元直接通过在实体等参数单元中引入结构中各类构件的基本假定而得出一种新型单元,根据不同的假定可以得到退化杆、退化梁、退化板壳单元等,其同时兼有一般空间等参元和板壳单元的优点[4, 5, 6, 7, 8]。
当采用该退化单元进行结构分析时,其位移插值模式与三维等参单元相同[9]。单元中的任一点的位移可以由单元节点位移根据形函数进行插值求得。根据材料本构关系和位移插值模式,采用数值积分格式求出单元刚度矩阵并组装成整体刚度矩阵。单元刚度矩阵的推导与数值积分格式可参见文献[6, 10]。
在钢筋混凝土结构承载力分析中,如何考虑钢筋的作用是计算的一个重要方面。在实体退化单元有限元分析中,将钢筋作为结构的一部分来考虑普通钢筋和有黏结预应力筋与混凝土一起参与结构的受力[11]。
设某实体退化单元中有一根钢筋,并假设钢筋轴向受力,不考虑其弯曲变形。采用三节点一维等参元(参数为t)对单元中钢筋的几何和位移进行描述,其节点编号见图 1。钢筋任意一点的几何坐标和位移均可通过3个节点的坐标和位移插值而得到,三节点单元的节点位移可由其所在实体退化单元的节点位移通过形函数插值得到。
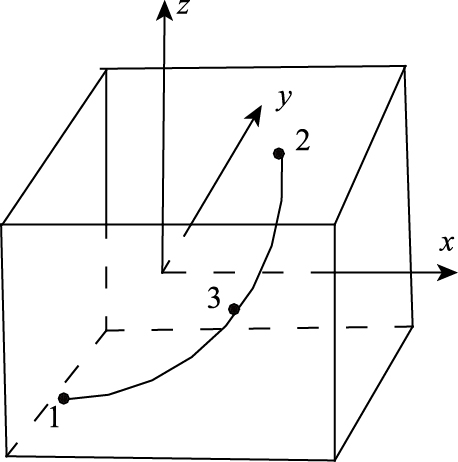
|
| 图 1 单元中钢筋示意图 Fig. 1 Schematic diagram of rebar in element |
钢筋上任意点处的切线矢量为v={l1,m1,n1},根据该矢量可求得钢筋的轴向应变,其表达式可以通过线性变换求得,见式(1):
式中,ε={εx,εy,εz,γyz,γzx,γxy}T,T={l12,m12,n12,m1n1,n1l1,l1m1}T。钢筋对实体退化单元刚度矩阵的贡献可采用分区数值积分技术,如式(2)所示:
式中,nm为单元中钢筋总分段数;Bi,Bj为实体单元中的应变-位移矩阵;J为实体退化单元中雅克比矩阵的行列式值;Jt为钢筋段雅克比矩阵的行列式值;Akg为第k段的钢筋截面积。在钢筋混凝土结构承载力分析中,另外一个重要的方面是如何考虑混凝土和钢筋的非线性材料行为。采用理想弹塑性材料模型模拟普通钢筋,采用线性强化材料模型模拟预应力钢筋,并用极限拉应变作为其破坏准则。采用Ohtani和Chen[12]的多轴塑性模型对混凝土弹塑性行为进行描述。为了克服应力空间的加卸载函数无法适应材料软化行为描述的缺点,该模型在应变空间中描述材料的塑性变形,能较好地表述塑性体积变化,并能考虑复杂应力状态对塑性变形发展的不同影响。根据该理论可得混凝土弹塑性切线刚度矩阵DT:
式中,D为根据实体退化单元理论修正后的弹性矩阵;σ为应力矢量;f为屈服面方程;A为强化参数;H(L)为阶梯函数: L为应变空间中的加、卸载函数: 式中dσe为弹性应力增量。采用正交弥散开裂模型模拟钢筋混凝土结构裂缝的发展,在一个材料积分点可考虑多方向开裂,同时假定一个积分点三向开裂视为结构破坏。当混凝土开裂后,采用开裂后的弹性刚度矩阵Dcri(i=1,2,3)来描述开裂后混凝土结构的弹性刚度矩阵D,这样就可以求得第i次开裂后材料的弹塑性切线刚度矩阵TDcri(i=1,2,3)。
2 有限元建模根据港珠澳大桥下部结构墩身的特点,本文选取了典型的135#墩进行承载能力分析。规定桥墩高度方向为X轴,桥墩横向为Y轴,桥墩纵向为Z轴。根据桥墩的结构特点,采用20节点三维实体虚拟层合退化板单元对135#墩进行分析,沿X轴方向划分21个单元,Y轴方向划分4个单元,沿Z轴方向划分为8~16个单元,桥墩单元总数为936个单元;根据实际材料分布情况,每个单元内部划为1~4层;钢筋按桥墩实际分布情况进行输入。边界条件为在桥墩承台处约束其3个方向位移。桥墩实体退化单元有限元网格及钢筋网格分别如图 2、图 3所示。
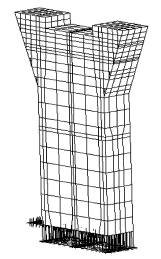
|
| 图 2 有限元模型 Fig. 2 Finite element model |
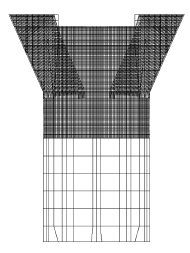
|
| 图 3 钢筋有限元网格图 Fig. 3 Finite element mesh of rebar |
在荷载方面,桥墩自重以体积力形式施加,桥墩重量取为2.60×104 N/m3,其方向竖直向下;三维空间预应力首先以等效外荷载形式直接施加到结构上,得到结构内力分布后把该内力状态及预应力钢筋的初始应力状态输入到结构中,实现对预应力效应的准确模拟;上部结构的自重通过在墩顶支座尺寸范围内施加方向向下的集中荷载进行模拟。
3 计算结果及讨论图 4示出了墩顶支座中心处随墩顶竖向荷载的增加,其沿横桥向和竖桥向的变位图。
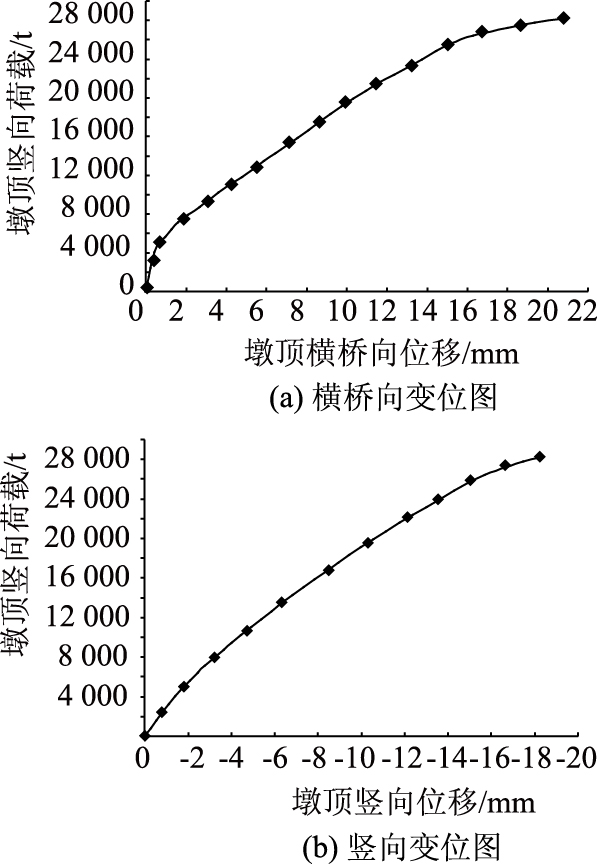
|
| 图 4 不同水平墩顶竖向荷载下墩顶支座中心处变位图 Fig. 4 Vertical displacements at bearing center on top of pier under different horizon loads |
计算结果表明:该桥墩的墩顶竖向极限荷载值为28 135.35 t;墩顶竖向开裂荷载值为4 860.0 t。以下将对各个加载阶段过程墩身受力及变形情况进行详细描述,同时为方便表述,记p为墩顶所施加的竖向荷载值。
根据不同荷载水平下结构的响应特点,可以将整个加载过程分为8个主要阶段,即弹性阶段、开裂阶段、二次开裂阶段、三次开裂阶段、钢筋受拉屈服阶段、钢筋受压屈服阶段、混凝土压碎阶段以及整体破坏阶段。
在弹性阶段,墩身结构基本处于弹性受力状态。此时,钢筋与混凝土应力均未超出弹性极限值。
当竖向荷载p达到4 860.0 t,即桥墩的开裂荷载时,墩顶在位于墩身上部横梁跨中顶部处(设计标高21.995 m处)出现少量沿顺桥向的水平裂缝。在当前荷载水平下,墩顶支座中心横桥方向的水平位移为0.570 mm。开裂阶段桥墩墩身的位移和应力分布情况如图 5所示。

|
| 图 5 开裂荷载阶段桥墩位移及应力情况 Fig. 5 Stress and displacement of pier in step of cracking |
当竖向荷载p大于开裂荷载时,墩身进入开裂阶段。墩身刚度随着荷载增大逐步降低。随着荷载逐步增大,裂缝沿着墩身上部横梁中部和其内部发展,并逐渐扩展至墩身中部。上述裂缝主要为桥墩顺桥向的水平裂缝和竖向裂缝,在水平裂缝和竖向裂缝产生的同时逐步伴随有斜裂缝产生。
当竖向荷载p增至8 734.03 t时,结构进入二次开裂阶段。裂缝形式主要表现为桥墩横梁中部部分混凝土出现二次开裂(即单元积分点两个方向应力达到混凝土抗拉强度)。墩身中部顺桥向墩壁与墩身上部连接区域压应力逐步加大,并由该区域向其四周形成逐渐扩散的压应力集中区。墩顶支座中心横桥向水平位移发展至15.195 mm。
当竖向荷载p增至10 223.01 t时,结构进入三次开裂阶段。墩身上部横梁顶部部分混凝土出现三次开裂情况,混凝土拉伸破坏。墩顶支座中心横桥向水平位移为3.608 mm。
当竖向荷载p增至11 033.01 t时,结构钢筋进入受拉屈服阶段。墩身上部横梁顶部部分横桥向普通钢筋拉伸屈服。此时,墩顶支座中心处横桥向水平位移为4.145 mm。随后,随着荷载逐渐增大,墩身上部支座下以及墩头中部部分普通钢筋出现受拉屈服;墩身上部横梁、墩身中部横桥向和竖向普通钢筋也部分出现受拉屈服。
当竖向荷载p达到22 372.2 t时,结构钢筋进入受压屈服阶段。墩身中部顺桥向墩壁与墩身上部连接部位有部分竖向普通钢筋出现受压屈服。墩顶支座中心处横桥向水平位移为12.331 mm。随后,随着荷载逐渐增大,该部位大部分竖向普通钢筋逐步出现受压屈服。
当竖向荷载p达到26 422.2 t时,结构混凝土进入压碎阶段。此时,墩身中部顺桥向墩壁与墩身上部连接处,出现混凝土压碎。墩顶支座中心处横桥向水平位移为16.261 mm。
当竖向荷载p达到28 135.35 t时,桥墩进入破坏阶段,桥墩发生整体破坏。此时,裂缝已经从墩顶扩展至下墩身。
从前面加载分析结果可以看出,墩身的破坏过程主要表现为墩身混凝土开裂、墩身上部横梁及墩身中部混凝土拉坏,墩身中部顺桥向墩壁混凝土与墩身上部连接处附近混凝土压碎以及墩身上部墩头底部混凝土压碎;普通钢筋出现大量拉、压屈服,从而使得桥墩丧失整体承载力。当桥墩破坏时,墩顶支座中心横桥向水平位移为20.75 mm。值得指出的是,在加载的整个过程中,桥墩中预应力钢筋尚未屈服;桥墩底部的混凝土未被压碎。桥墩在破坏阶段的位移及应力分布情况如图 6所示。
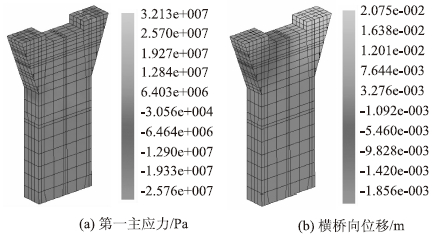
|
| 图 6 极限荷载阶段桥墩位移及应力情况 Fig. 6 Stress and displacement of pier in step of ultimate load |
由于环境等影响因素,下部结构的施工在跨海大桥建设中处于关键地位。埋床法全预制墩台及钢管复合桩技术为这类桥梁的施工提供了重要的技术手段。本文以港珠澳大桥工程为背景,采用实体退化单元,对埋床法全预制桥墩墩身的承载力进行了评估,探讨了桥墩结构加载过程墩身中部变形、混凝土及钢筋应力的变化情况,计算结果可为桥墩结构安全评估及优化设计提供科学依据。通过研究得知:
(1) 相对于传统有限元方法中的实体单元,基于实体退化单元的极限承载能力分析方法具有建模过程简单,划分单元少,计算结果准确可靠等特点,对于桥墩等典型实体结构分析中具有较好的适用性和通用性。
(2) 根据承载力分析的不同阶段,可以将预制桥墩整个加载过程分为弹性阶段、开裂阶段、二次开裂阶段、三次开裂阶段、钢筋受拉屈服阶段、钢筋受压屈服阶段、混凝土压碎阶段以及整体破坏阶段,可据此控制桥墩设计。
(3) 所计算桥墩在设计荷载作用下,其正常使用状态的钢筋应力处于较低水平,局部区域存在微裂,对结构安全、耐久性无影响,结构承载能力满足要求。
| [1] | 赵传林, 徐波, 秦观.港珠澳大桥超大型预制墩台吊装工艺探讨[J].中国港湾建设,2013(6):50-52. ZHAO Chuan-lin, XU Bo, QIN Guan.Discussion on Technology for Handling Super Large Precast Piers for HongKong-Zhuhai-Macao Bridge[J].China Harbour Engineering,2013(6):50-52. |
| [2] | 苏权科.跨海大桥特殊技术问题探讨[J].公路交通科技,2005,22(12):101-104. SU Quan-ke.An Analysis of Special Techniques for Sea-crossing Bridge[J].Journal of Highway Transportation Research and Development,2005,22(12):101-104. |
| [3] | 方明山.港珠澳大桥非通航孔桥下部预制墩台设计关键技术[J].中外公路,2015,35(1):112-117. FANG Ming-shan.Key Design Technology of Prefabricated Bridge Pier of Non-navigable Sea-crossing Bridge of HongKong-Zhuhai-Macao Bridge[J].Journal of China & Foreign Highway,2015,35(1):112-117. |
| [4] | 袁志军, 吴光宇, 扶名福.三维实体退化虚拟层合梁单元在梁极限承载力分析中的应用[J].南昌大学学报:理科版,2011,35(1):47-51. YUAN Zhi-jun, WU Guang-yu, FU Ming-fu.Analysis of Ultimate Load Capacity for Beam Using Degenerated Three-dimensional Solid Virtual Laminated Beam Element[J].Journal of Nanchang University:Nature Science Edition,2011,35(1):47-51. |
| [5] | 黄乔,孙永明,唐海红.虚拟层合单元与杆单元在桥梁预应力混凝土结构分析中的合成方法[J].公路交通科技,2008,25(4):84-88. HUANG Qiao, SUN Yong-ming, TANG Hai-hong.Method of Combining Virtual Laminated Elements and Bar Elements for Analysis of Prestressed Concrete Bridge Structures[J].Journal of Highway Transportation Research and Development,2008,25(4):84-88. |
| [6] | 汪劲丰, 吴光宇, 林泉, 等.预应力混凝土曲线桥极限承载能力分析[J].工程力学,2008,25(8):85-91. WANG Jin-feng, WU Guang-Yu, LIN Quan, et al.Study on the Ultimate Load Capacity of Prestressed Concrete Curved Bridge[J].Engineering Mechanics,2008,25(8):85-91. |
| [7] | 亓兴军, 项贻强, 李小军, 等.预应力混凝土桥梁分析的虚拟层合单元法[J].公路交通科技, 2006,23(8):76-80. QI Xing-jun, XIANG Yi-qiang, LI Xiao-jun, et al.Analysis of Prestressed Concrete Bridge with Virtual Laminated Element Method[J].Journal of Highway Transportation Research and Development,2006,23(8):76-80. |
| [8] | 牛辉, 汪劲丰, 张巍, 等.基于实体退化单元的高墩非线性稳定仿真分析[J].浙江大学学报:工学版,2012,46(6):1082-1089. NIU Hui, WANG Jin-feng, ZHANG Wei, et al.Simulation Analysis of Nonlinear Stability of High Pier Based on Degenerated Solid Element[J].Journal of ZheJiang University:Engineering Science Edition,2012,46(6):1082-1089. |
| [9] | 王勖成, 邵敏.有限单元法基本原理与数值方法[M].北京:清华大学出版社, 1995. WANG Xu-cheng, SHAO Min.Basic Principle and Numerical Method of Finite Element Method[M].Beijing:Tsing Hua University Press, 1995. |
| [10] | 凌道盛, 张金江, 项贻强, 等.虚拟层合单元法及其在桥梁工程中的应用[J].土木工程学报,1998,31(3):22-29. LIN Dao-sheng, ZHANG Jin-jiang, XIANG Yi-qiang, et al.The Method of Virtual Laminated Element and Its Application in Bridge Engineering[J].China Civil Engineering Journal,1998,31(3):22-29. |
| [11] | KANKAM J A, DAGHER H J.Nonlinear FE Analysis of RC Skewed Slab Bridges[J]. |
| [12] | OHTANI Y, CHEN W F.A Plastic-softening Model for Concrete Materials[J]. |
 2016, Vol. 33
2016, Vol. 33