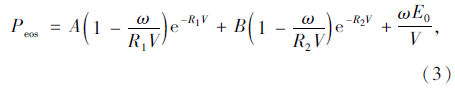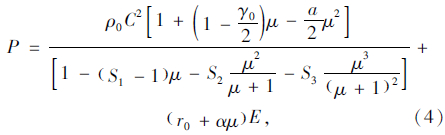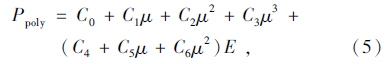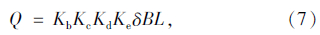扩展功能
文章信息
- 吴亮, 谢先启, 韩传伟, 许锋, 蔡路军
- WU liang, XIE Xian-qi, HAN Chuan-wei, XU Feng, CAI Lu-jun
- 高架桥箱梁水压拆除爆破数值模拟与实践
- Numerical Simulation and Practice of Hydraulic Demolition Blasting of Viaduct Box Girder
- 公路交通科技, 2016, Vol. 33 (3): 64-70
- Journal of Highway and Transportation Research and Denelopment, 2016, Vol. 33 (3): 64-70
- 10.3969/j.issn.1002-0268.2016.03.011
-
文章历史
- 收稿日期: 2014-12-14
2. 武汉爆破有限公司, 湖北 武汉 430023
2. Wuhan Blasting Engineering Co., Ltd., Wuhan Hubei 430023, China
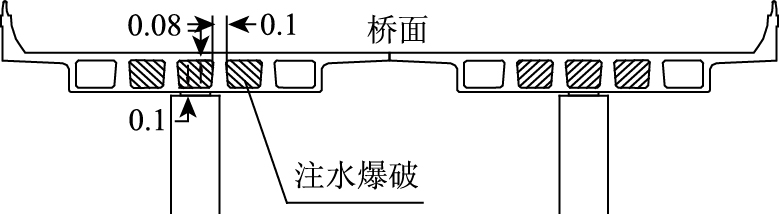
近年来,随着城市拆除对爆破技术要求的提高,水压爆破技术在国内得到广泛的应用[1, 2, 3, 4, 5, 6]。水压爆破通过炸药爆炸在水中产生的冲击波和气泡脉动来破坏介质,不仅具有药包个数少、爆破网路简单、能量利用率高等特点,而且具有破碎效果好、爆破噪音低且安全性高等优点。针对水压爆破的优点,在某城市高架桥拆除工程中,对相邻墩柱间的箱梁实施了水压爆破技术。该跨总长度为18 m,两端帽梁各1 m,爆破长度为16 m,每个注水腔体平均分置6个药包,左右两侧共6个注水腔体,共计36个药包,每个药包重0.3 kg。水压爆破区域剖面示意图见图 1。
|
| 图 1 水压爆破区域剖面示意图(单位:m) Fig. 1 Schematic diagram of cross-section of water pressure blasting area(unit:m) |
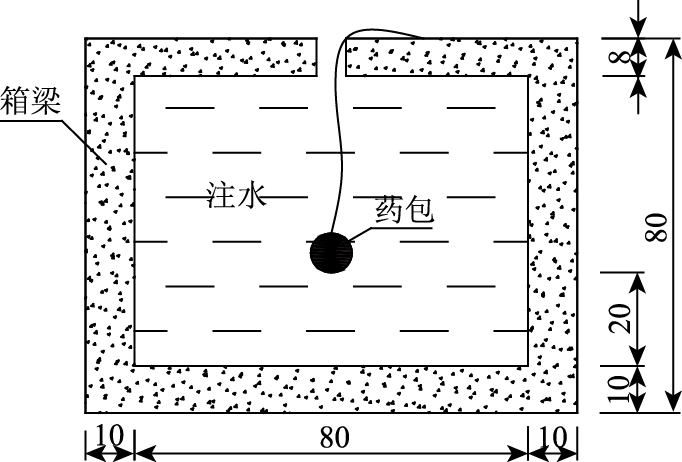
根据箱梁的结构特点及破碎效果要求,在桥面进行钻孔注水,放入药包。箱梁尺寸与药包位置见图 2。
|
| 图 2 装药结构示意图(单位:cm) Fig. 2 Schematic diagram of charge structure (unit:cm) |
混凝土与岩石JHC(Johnson-Holmquist-Cook)模型是一种适用于大变形下、高应变率的材料模型。它与金属材料中应用广泛的Johnson-Cook材料模型类似,其等效屈服强度是应变率、损伤及压力的函数,损伤量则是等效塑性应变、塑性体应变和压力的函数,计算参数分别为[7, 8]:ρ0=2 440 kg/m3,E=35.7 GPa,ν=0.2,G=14.86 GPa,A=0.79,B=1.6,C=0.007,N=0.61,fc=0.048 GPa,T=0.004 GPa,Efmin=0.01,Sfmax=7.0,Pcrush=0.016 GPa,ucrush=0.001,Plock=0.8 GPa,ulock=0.1,D1=0.04,D2=1.0,K1=85.0 GPa,K2/GPa=-171.0 GPa,K3=208.0 GPa,EPS0=1.0×10-6。
1.2 炸药状态方程在数值模拟中,LS-DYNA在桥梁结构动力分析方面具有很高的计算精度[9, 10],并且LS-DYNA程序[11]基于炸药的爆轰研究成果并结合爆生气体的状态方程来描述整个爆腔的动力膨胀过程,可以精确描述炸药爆轰时的压力变化历程。美国Lee等学者在Jones 和Wilkins 的工作基础上提出JWL方程,其一般形式为:
式中,Peos为由JWL状态方程决定的压力;V为相对体积;E0为初始比内能,A,B,R1,R2,ω分别为描述JWL方程的5个独立物理常数。炸药参数取值分别为[8]:ρ=1 300 kg/m3,D=4 000 m/s,A=214.4 GPa,B=0.182 GPa,R1=4.2,R2=0.9,ω=0.15,E0=4 192 MJ/m3。空气密度取为1.29 kg/m3,压力采用线性多项式状态方程(*EOS_LINEAR_POLYNOMIAL)模拟。
1.3 水和空气状态方程水材料采用MAT_NULL材料模型,通过Gruneisen状态方程*EOS_GRUNEISEN描述,见式(4):
式中,C为Us-Up曲线斜率的系数;γ0为Gruneisen参数;α为对γ0的修正;μ=ρ/ρ0-1;相关参数见文献[6]。空气密度取为1.29 kg/m3,压力采用线性多项式状态方程(*EOS_LINEAR_POLYNOMIAL)模拟,其方程表达式为:
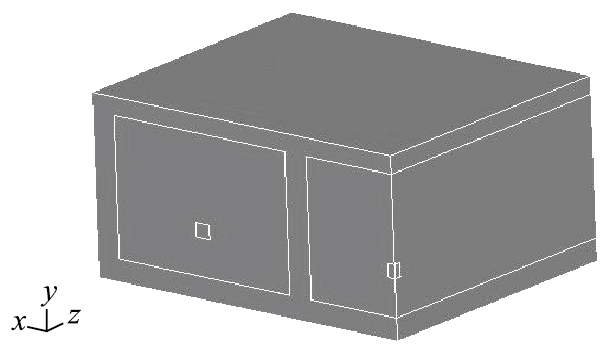
式中,C0~C6为常数;μ为比体积;E为内能与初始体积之比。上述方程中各系数取值如下:C0=C1=C2=C3=C6=0.0,C4=C5=0.4。 1.4 计算模型计算模型采用某高架桥拆除工程中的两相邻墩柱间的箱梁尺寸,根据爆破参数,取箱梁跨中长为2.28 m的梁段,三并排箱梁断面为2.6 m×0.8 m,每个空腹腔断面为0.8 m×0.6 m,空腹腔内充满水。为了建模方便,将药包看作正方体药包,布置于空腹腔中心偏下位置,距底部0.2 m处,药包边长为0.062 m。为简化计算,取箱梁的1/4模型,将钢筋的材料性能分散到混凝土当中,将两者看作一种材料进行分析,如图 3所示。整体式模型优点是建模方便,分析效率高,但是缺点是不适用于钢筋分布较不均匀的区域,且得到钢筋内力状态比较困难,主要用于有大量钢筋且钢筋分布较均匀的构件中。分离式有限元模型是将钢筋和混凝土两种材料采用不同的单元分别建立有限元模型,其特点是混凝土单元刚度矩阵、钢筋单元刚度矩阵是分别计算的,然后统一集成到整体刚度矩阵中;其优点是可以按实际配筋划分单元,必要时可以在钢筋与混凝土之间嵌入联结单元来模拟钢筋和混凝土之间的黏结和滑移,并分别研究二者的破坏过程,其缺点是,当钢筋量大且不规则时,划分单元的数量很大。
|
| 图 3 计算模型 Fig. 3 Calculation model |
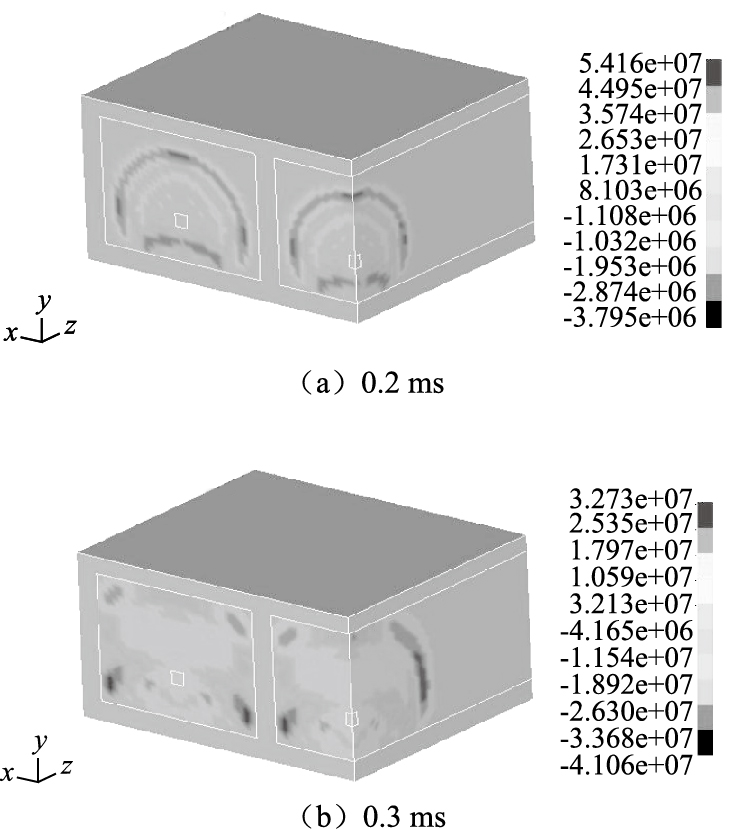
取1/4模型,水压爆破数值模拟结果如图 4、图 5所示。从图中可以再现水中冲击波的传播过程和爆生气体气泡膨胀作用过程。炸药起爆后,向水中传播冲击波。在100 μs时刻左右冲击波开始作用于箱梁底板,压力峰值约125 MPa,压缩冲击波作用于壁体后产生反射,反射波最初表现出刚性反射的压缩性质,而后表现为稀疏性质,随后入射波又剧烈地衰减,因此在底部面板附近水中开始呈现拉伸状态,由于水不能承受拉力,因而产生空泡,阻止压力下降,即产生空化现象,见图 4(a)底部水域深色区。冲击波以球面波形态继续向箱梁腹板传播,并反射形成空化区,见图 4(b),在300 μs时刻,箱梁腹腔下部两侧以及顶部为空化区。
|
| 图 4 水中冲击波传播时程云图(单位:Pa) Fig. 4 Nephogram of propagation process of shock wave in water(unit:Pa) |

|
| 图 5 爆生气体气泡膨胀过程 Fig. 5 Bubble expansion process of detonation gas |
爆生气体的膨胀过程见图 5。爆生气体(即气泡)的膨胀过程相对于爆炸冲击波的传播要慢,在0.8 ms时刻,爆生气体膨胀到箱梁底部翼缘,底板混凝土开始破坏;在4.3 ms时刻,爆生气体膨胀到箱梁顶部翼缘,顶板混凝土开始破坏。
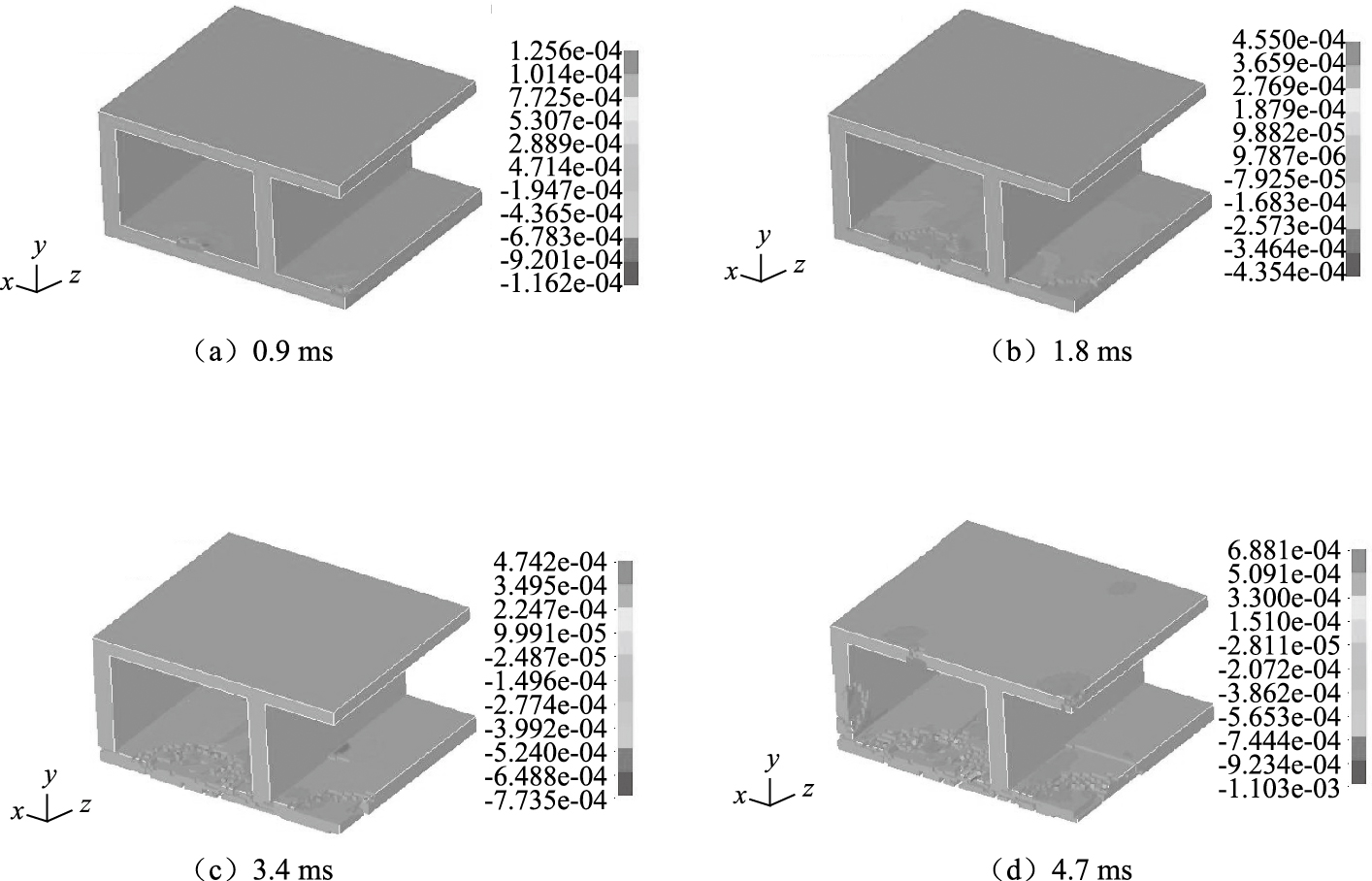
2.2 混凝土壁受力分析箱梁不同时刻破碎情况见图 6。在0.9 ms时刻,底部面板受压开始破坏,由中间单元开始向四周呈圆形发展破坏,底部面板介质在冲击压缩荷载作用下向下运动,形成纵向的张拉裂纹,随后,在底部翼缘与腹板连接处受弯发生剪切-拉伸破坏,底部翼缘与腹板连接处裂纹进一步扩展,在3.4 ms时刻,底部面板产生横向的剪切裂纹;在4.7 ms时刻,顶部面板单元开始破坏,顶部面板的破坏机理与底部面板的破坏机理相同。
|
| 图 6 箱梁破坏过程 Fig. 6 Damage process of box girder |
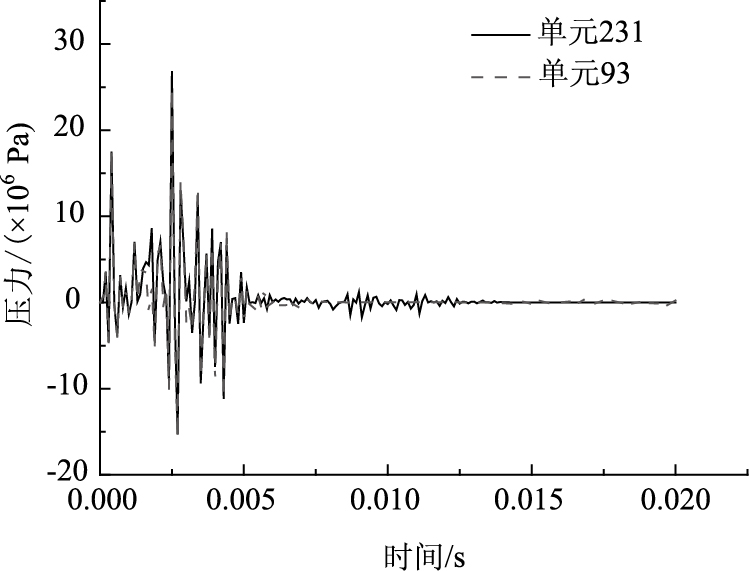
外侧腹板受载后,介质向外运动,产生拉伸的纵向裂纹和横向的剪切裂纹。但两相邻空腹腔间的隔梁没有破坏,这是由于两边施加的爆破荷载基本对称,使间腹板两边处于受压状态,由于压差很小,见图 7,因此不利于墙体产生变形位移隔梁没有产生位移的运动空间会使间隔墙达不到爆破破碎要求,所以,要使隔梁也达到良好的破碎效果,建议采用微差爆破技术,或者交叉布药方案。
|
| 图 7 两水箱间腹板中间处水体单元压力 Fig. 7 Element pressure on web between both adjacent water boxes |
鉴于相邻药包布置在同一断面、同时起爆不利于隔梁破碎的情况,对交叉布置药包的情况进行了计算,破碎效果见图 8(b)。

|
| 图 8 箱梁水压爆破(单位:Pa) Fig. 8 Explosive distribution(unit:Pa) |
对比图 8,计算结果显示,交叉布药同时起爆的方案隔梁满足爆破破碎要求,整体爆破效果比同一断面布药效果好。主要原因在于交叉布药爆破时,作用在隔墙两边的冲击荷载有先后,利于墙体产生变形位移,见图 9。

|
| 图 9 两水箱间腹板中间处水体单元压力(交叉布药)(单位:Pa) Fig. 9 Water element pressure in middle of web between both adjacent water boxes with explosive cross arrangement(unit:Pa) |
对于隔离的两个水箱是可以采用微差起爆的,但水压爆破箱梁间微差间隔时间是爆破效果好坏的关键[12]。若微差间隔时间选取过小,当相邻水箱药包相继起爆后,间隔墙两边压差不显著,将不利于墙体产生变形位移,从而影响爆破效果;微差间隔时间过大,后续药包起爆时一侧的间隔墙已被破坏,水体的泄漏将影响其他箱壁的破碎效果。
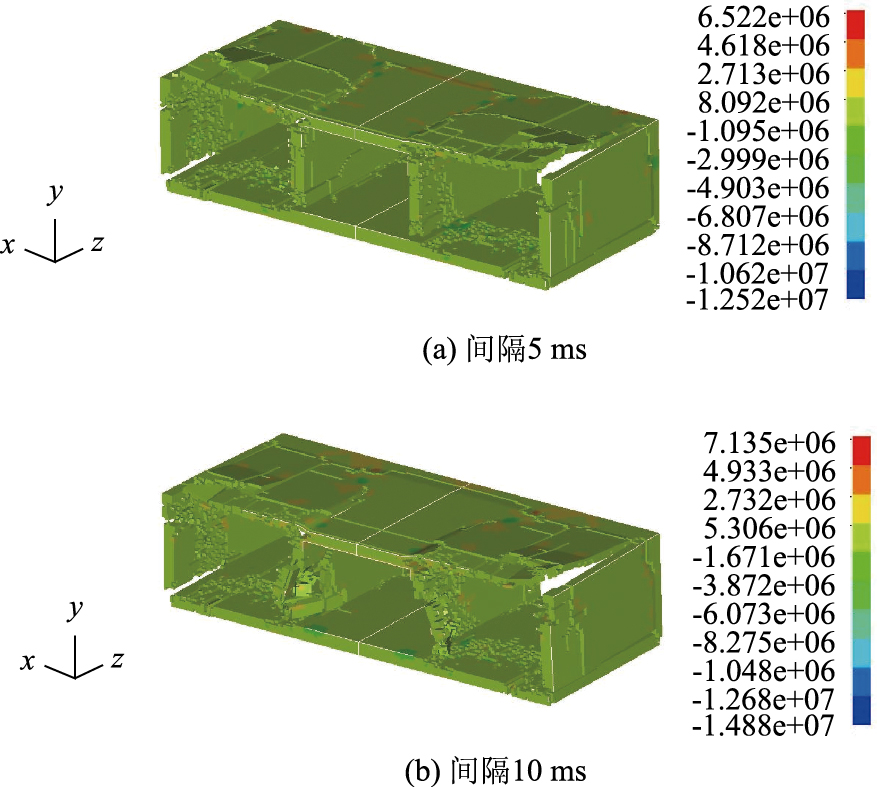
计算选取微差间隔时间为5 ms和10 ms两种工况。比较两种工况计算结果,中隔梁均出现裂纹,间隔10 ms情况下中隔梁位移明显,局部破碎程度更高,见图 10。间隔5 ms情况下,两水箱间腹板中间处水体单元压力见图 11(a),当一侧的炸药爆炸后冲击波到达中隔梁并进行作用,时段为0~2.5 ms,中隔梁受到扰动引起相邻水体反应,时段为2.5~7.5 ms,相邻水体单元的响应曲线频率比先爆水箱的水体响应曲线频率低,有利于中隔梁的破坏,随后相邻炸药爆炸引起水体进一步的反应,在5.1 ms时刻开始叠加。间隔10 ms情况下,后爆引起水体与先爆引起的水体响应已分开,见图 11(b)。可见,微差时间选择既要使间隔梁有充分的位移破坏,也要保证避免水体的泄漏造成能量的流失。本工程的相邻水箱爆破微差间隔时间选取5 ms较合理。
|
| 图 10 箱梁水压爆破(单位:Pa) Fig. 10 Hydraulic demolition blasting (单位:Pa) |

|
| 图 11 两水箱间腹板中间处水体单元压力(单位:Pa) Fig. 11 Water element pressure in middle of web between both adjacent water boxes(unit:Pa) |
该爆破工程采用主桥爆破拆除、两端引道机械拆除的总体拆除方案。主桥爆破方案采用一次点火起爆,自中间(84#墩)分别向南北两端逐排延时,延时总长为24.77 s。爆破飞石、冲击波等有害效应采用覆盖防护、近体防护和保护性相结合的综合防护措施。地下管线采用铺设钢板、沙袋墙、废旧轮胎等减振措施。桥面上布置双向近4 km的爆炸水雾降尘水袋。同时,爆破时在桥体两侧200 m范围内共布置了10条爆破振动监测线,并对爆破粉尘浓度、地应力等项目进行了实时监测。
3.1 药量计算工程实践表明:使用冲量准则公式的药量计算公式与爆破结果的符合程度较高。冲量准则公式是利用薄壁圆筒的弹性理论,把水压爆破产生的水击波看成冲量作用的结果,并运用结构物在等效静载作用下产生位移与在冲量作用下产生的位移相同的原理计算得出的药量计算公式。
由于本工程为长筒方形结构,结合箱梁形状尺寸,冲量准则公式为:
式中,Q为药包质量;Kb为与爆破方式有关的系数,本工程为封闭式,取1.0;Kc为与材质有关的用药系数,本工程为钢筋混凝土,取1.0;Kd为结构调整系数,本工程为方形,取1.0;Ke为炸药换算系数,本工程取1.0;B为结构物短边边长;L为结构物长度;δ为结构物壁厚。经计算,单个注水腔体的总装药量约为1.6 kg。等分成6个药包后,取每个药包0.3 kg。本水压爆破共计36个药包,总装药量约为10.8 kg。
3.2 药包布置对封口箱梁,保证上部桥面的破坏条件是水应充满整个箱梁,即保证水中爆炸冲击波能作用到上部桥面梁板,可以将箱梁上部桥面板作为容器的一个壁来布置药包。药包的具体布置见图 2。
水压爆破应选用密度大、耐水性好的炸药,本次水压爆破采用2号岩石乳化炸药。药包施工中采用悬挂式方式,并附加了配重防止药包移位。
3.3 起爆网路为了提高起爆的可靠性,本次水压爆破采用导爆管雷管引爆水中的药包。药包起爆雷管(MS16)引出箱梁后捆扎,用MS1段导爆管雷管接力引入桥体主起爆网络,与55#墩柱同时起爆,起爆网路图见图 12。

|
| 图 12 网络联接示意图 Fig. 12 Schematic diagram of blasting network connection |
箱梁水压爆破拆除与未采用水压爆破拆除的爆后效果见图 13、图 14。采用水压爆破箱梁路面破碎,而未采用水压爆破的路桥箱梁路面完整,从而增加了机械拆除的工作量。数值计算结果基本上反映了水压爆破实际爆破效果,表明采用数值仿真技术可以很好地从力学角度揭示箱梁水压爆破的破坏机理,再现箱梁水压爆破的破坏过程,预判爆破参数对爆破效果的影响。

|
| 图 13 水压爆破箱梁的桥面效果 Fig. 13 Blasting effect of box girder at bridge deck with hydraulic demolition blasting |

|
| 图 14 未采用水压爆破的箱梁桥面效果 Fig. 14 Blasting effect box girder at bridge deck with conventional method |
(1)路桥箱梁相邻水箱对称同时起爆情况下,隔梁两侧压差很小,不利于隔梁产生变形和破坏,达不到爆破破碎要求。
(2)采用交叉布药同时起爆的方案时,隔梁满足爆破破碎要求,主要原因在于交叉布药爆破时,作用在隔墙两边的冲击荷载有先后,利于墙体产生变形位移。
(3)对称布药情况下,本工程的相邻水箱爆破微差间隔时间建议选取5 ms较合理,既能使间隔梁有充分的位移破坏,也避免水体的泄漏而造成能量的流失。
(4)箱梁的破坏效果与实际爆破效果相吻合,表明采用数值仿真技术可以很好地从力学角度揭示箱梁水压爆破的破坏机理,再现箱梁水压爆破的破坏过程,预判爆破参数对爆破效果的影响,对水压爆破拆除技术的发展起到巨大的推动作用,并能充分展现其安全高效、经济环保的爆破效果。
| [1] | 范学臣, 刘学庆,纪臻,等.胶州湾高速环太原路立交桥水压爆破拆除[J]. 工程爆破,2011,17(3):62-65. FAN Xue-chen, LIU Xue-qing, JI Zhen, et al. Hydraulic Blasting Demolition of Taiyuan Road Overpass on Jiaozhou Bay High-speed Highway[J]. Engineering Blasting,2011,17(3):62-65. |
| [2] | 冯剑平,李志利. 爆破技术与数值模拟在桥梁拆除中的应用[J]. 现代交通技术,2013,10(5):38-42. FENG Jian-ping, LI Zhi-li. Application of Blasting Technique and Numerical Simulation in Bridge Demolition[J]. Modern Transportation Technology,2013,10(5):38-42. |
| [3] | 施富强,杨旭升,李文全,等.田庄台辽河公路大桥控制爆破拆除技术分析[J]. 工程爆破,2009,15(3):50-54. SHI Fu-qiang, YANG Xu-sheng, LI Wen-quan, et al. Technical Analysis on Controlled Blasting Demolition of Big Bridge of Liaohe Highway in Tianzhuangtai[J]. Engineering Blasting,2009,15(3):50-54. |
| [4] | 罗德丕,池恩安.城市中心公路立交桥的水压爆破拆除[J]. 矿业研究与开发,2012,32(3):111-114. LUO De-pi, CHI En-an. Demolition of a Highway Overpass in Downtown Area by Hydraulic Blasting[J].Mining Research and Development,2012,32(3):111-114. |
| [5] | 穆大耀,李征文,李金平.水压爆破拆除20 m长钢筋砼预应力空心板危桥[J]. 爆破,2005,22(4):99-101. MU Da-yao, LI Zheng-wen, LI Jin-ping. Demolition of a Dangerous 20 m Prestressed Concrete Cored Slab Bridge by Hydraulic Blasting[J]. Blasting,2005,22(4):99-101. |
| [6] | 杨忠华,杨军,陈大勇. 混凝土拱座空心立柱水压爆破数值模拟研究[J].爆破,2010,27(4):70-73. YANG Zhong-hua, YANG Jun, CHEN Da-yong. Study on Water Pressure Blasting of Reinforced Arch Seat and Hollow Pillar in Numerical Simulation[J]. Blasting,2010,27(4):70-73. |
| [7] | HOLMQUIST T J, JOHNSON G R. A Computational Constitutive Model for Concrete Subjected to Larger Strains, High Strain Rates and High Pressure[C]//14th International Symposium Ballistics. Quebec City, Canada:Erican Defense Preparedness' Association, 1995:591-600. |
| [8] | 吴亮,钟冬望,卢文波. 空气间隔装药爆炸冲击荷载作用下混凝土损伤分析[J].岩土力学,2009,30(10):3109-3114. WU Liang,ZHONG Dong-wang,LU Wen-bo. Study on Concrete Damage under Blast Loading of Air-decking[J].Rock and Soil Mechanics,2009,30(10):3109-3114. |
| [9] | 桂水荣,陈水生,赵辉,等.基于LS-DYNA公路桥梁车桥耦合振动模型[J].公路交通科技,2013,30(7):40-45. GUI Shui-rong,CHEN Shui-sheng,ZHAO Hui,et al. Model of Highway Bridge Subjected to Vehicle-bridge Coupled Vibration Based on LS-DYNA[J]. Journal of Highway and Transportation Research and Development,2013,30(7):40-45. |
| [10] | 廖雪娇,王建国,尹光志,等.减低交通荷载引起地面振动的三维数值分析[J].公路交通科技,2010,27(11):43-48. LIAO Xue-jiao, WANG Jian-guo, YIN Guang-zhi, et al. 3D Numerical Analysis for Traffic Reduction Induced Ground Vibration[J]. Journal of Highway and Transportation Research and Development,2010,27(11):43-48. |
| [11] | Livermore Software Technology Corporation. LS-DYNA Keyword User's Manual[M]. Livemore:Livermore Software Technology Corporation,2003. |
| [12] | 谢俊杰,龙源,吴腾芳,等.水压爆破在特殊结构构筑物拆除中的应用技术[J].工程爆破,2005,11(4):50-53. XIE Jun-jie, LONG Yuan, WU Teng-fang, et al. Application Technology of Water Pressure Blasting to Demolish of Especial Structure Building[J]. Engineering Blasting,2005,11(4):50-53. |
 2016, Vol. 33
2016, Vol. 33