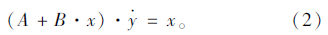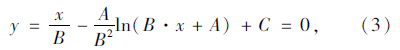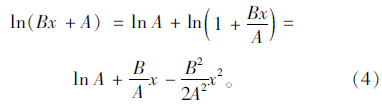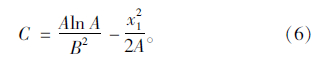扩展功能
文章信息
- 刘平, 许慧, 璆玮
- LIU Ping, XU Hui, QIU Wei
- 大跨度斜拉索自重下的垂度分析
- Analysis of Deadweight Induced Sag of Long-span Stay Cable
- 公路交通科技, 2016, Vol. 33 (3): 60-63
- Journal of Highway and Transportation Research and Denelopment, 2016, Vol. 33 (3): 60-63
- 10.3969/j.issn.1002-0268.2016.03.010
-
文章历史
- 收稿日期: 2014-11-27
2. 安徽理工大学 土木工程学院, 安徽 淮南 232000
2. School of Civil Engineering, Anhui University Of Science & Technology, Huainan Anhui, 232000, China
斜拉索以其优越的跨越能力、合理的受力特点及新颖的结构形式、美观的表观造型,成为现代桥梁工程中发展最快、革新最快、最具竞争力的桥型之一[1, 2, 3, 4]。斜拉索作为斜拉索桥梁当中最重要的受力构件,承担着结构大部分的荷载。由于斜拉索刚度小、重力拉力比低等特点,其几何非线性特点非常突出[5, 6]。在各种非线性影响因素中,以大位移与斜拉索垂度的影响最大[7, 8, 9, 10]。传统考虑垂度影响的方法是采用Ernst公式,该公式由德国工程师Ernst于1932年首先提出,考虑了重力对于斜拉索垂直方向影响效应。该方法形式简单,物理意义明确,为业界广泛接受。但是,在他的方法中,忽略了重力在斜拉索方向分量的影响,因此,斜拉索挠度曲线为悬链线。在最大挠度与拉索长度比为小量的情况下,进一步假设拉索挠度曲线为二次抛物线。事实上,在工程上拉索应力、密度、长度范围内,以抛物线代替悬链线是合理的,而忽略重力在斜拉索方向分量的影响却值得商榷。
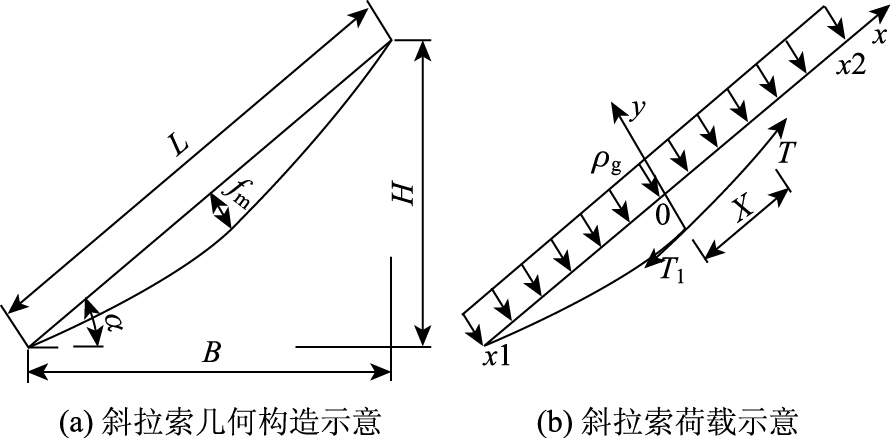
1 方程与求解斜拉索作为斜拉桥的主要受力构件,在施工过程中及桥梁成形后,所受的力主要有自重及张拉力(风、雨荷载不直接作用于张拉索)及拉索端点振动力或偶尔如地震等作用。在静力分析时,不考虑拉索端点约束及偶然振动,其受力示意如图 1所示。其中,L为拉索直线长度(也就是两端点距离),H为拉索竖直方向投影长度,B为拉索水平方向投影长度,α为拉索长度方向与水平方向的夹角,y为拉索挠度,fm为挠度最大值。
|
| 图 1 斜拉索受力示意 Fig. 1 Schematic diagram of cable force |
由泰勒中值定理可知,斜拉索在x1及x2之间必然存在某点,使得其一阶导数值y·=0,设在此位置斜拉索的张拉力为T0。以此为原点、拉索方向为x轴、垂直拉索方向为y轴建立坐标系;设拉索下端点处坐标为x1,拉索上端点处坐标为x2,显然有x2-x1=L,图例见图 1。令m=ρg·A,根据斜拉索长度方向上的受力平衡条件建立方程有:
显然,如果α=0,则方程简化为水平拉索,可以知道,此解为悬链线方程[11];如果α=π/2,此解为一直线(加上边界条件,可以确定其解为竖直直线)。
1.2 方程讨论与求解在α≠0的情况下,从理论上讲,式(1)也可以求得解析解。不过,由于解过于复杂,物理意义不明显。因此,根据实际物理条件限制,对此方程作一些适当简化,以突出方程及解的物理意义,适应工程需要。
首先,由于 与1相比为小量,忽略
与1相比为小量,忽略 的二阶小量,可以有:
的二阶小量,可以有: ,并令:
,并令:

式中,σ0为拉应力值,取值为700~1 100 MPa;ρ为拉索折合密度(包括套管、油脂及装饰物重量),可取20×103 kg/m3;g为重力加速度,可取10[12, 13, 14]。将此假定与变换式代入式(1),有:
边界条件为:左右两端端点值 y(x1)=y(x2)=0,且有x2-x1=L。求解式(2)并且代入边界条件可得拉索挠度方程为:
式中,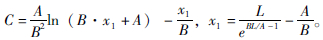 因此,斜拉索考虑重力全效应时的长度即为式(3)对拉索长度(x)的积分值,积分结果为:
因此,斜拉索考虑重力全效应时的长度即为式(3)对拉索长度(x)的积分值,积分结果为:
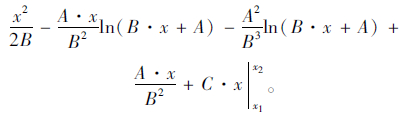
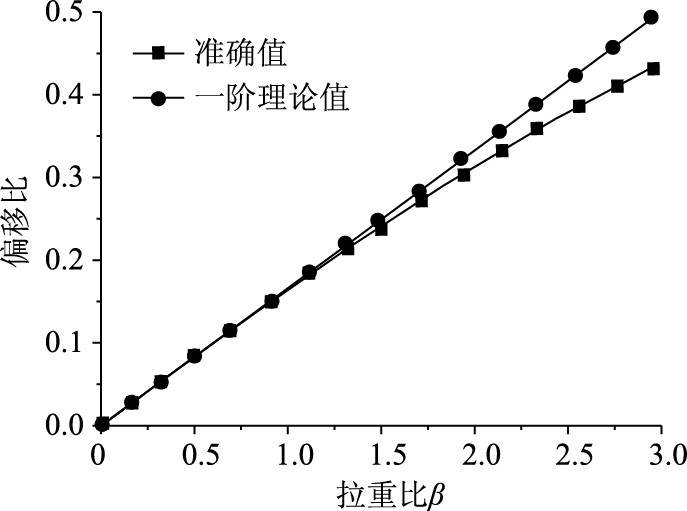
上述经过简化后的求解结果仍然较为复杂,物理意义不明显。为了获得较为明确的物理意义,对上述结果进行再一次简化,令 当β为小量时,显然有
当β为小量时,显然有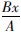 同样为小量。忽略β三次项以上高阶项,对于对数函数有:
同样为小量。忽略β三次项以上高阶项,对于对数函数有:
同时,由式(3)可知,方程的形式为对数函数,与一般常用假设挠度为二次抛物线是不同的。但是,如果忽略二阶小量,将式(4)代入式(3)中,有:


方程即为二次抛物线,此结果表明,在忽略二阶小量的情况下,尽管拉索悬垂形状不是悬链线,假定其为抛物线仍然是合理的。不过,值得注意的是,此方程并不满足所有的边界条件,对于拉索下方端点x=x1时,方程挠度值y=0;对于拉索上方端点x=x2,方程挠度值 ,并不为零。
,并不为零。
对于x1,x2,C分别忽略二阶小量,可以有:
可以看出,x1,x2的值相当于在拉索中心有个偏移量,此偏移数值与拉索半长的比值为|x1-L|=β/6。此偏移值也可以认为是挠度最低点位置由拉索中心处向重力方向的偏移值。从图 2可以看出,偏移比在拉重比β<1.5时,呈一次线性关系;只有在β较大时,与一阶理论值误差才逐步增大。
|
| 图 2 偏移比与拉力/重力比曲线 Fig. 2 Curves of offset ratio vs. tensile-weight ratio |
在工程应用中考虑拉索垂度效应最常用的方法是利用Ernst公式,其基本考虑是假定垂度引起的拉索曲线为左右对称二次抛物线;并且,其垂度与拉索长度相比为小量。这种假定实际上只考虑了拉索重力在拉索法向上的分量而忽略了重力在拉索长度方向分量的影响。根据其基本假定,由于垂度效应所引起的拉索挠度与拉索伸长量为[15, 16]:
本文综合考虑拉索自重在拉索方向与垂直拉索方向的影响,在忽略β的二阶项时,垂度影响下的挠度值为:
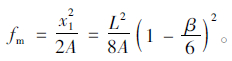
与Ernst的值相比,即相当于乘以一个系数值(1-β/6)2。同样,在计算拉索长度时忽略高阶小量,对于式(5)有: =x/A,对拉索长度积分可得拉索长度为:
=x/A,对拉索长度积分可得拉索长度为:
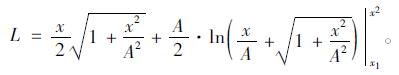
由于假定x/A为小量,因此忽略L中的x/A高阶小量后的结果为:L=x+x3/6A,代入积分上下限x1,x2后的化简结果为:

与Ernst公式相比,即相当于乘以一个系数值(1+β2/12)。值得注意的是,考虑重力横向效应时,拉索的挠度减小,而伸长量却是增加的。
3 结论斜拉索在张拉力与重力作用下的垂度效应是一种典型的几何非线性现象。一般做法是考虑拉索重力对于垂直拉索的影响,而忽略拉索重力在拉索方向上的分量。在这种假设下,拉索方向上的拉力分量为定值,所得的拉索形状为悬链线[17]。本文综合考虑到重力在垂直拉索方向与平行拉索方向的效应,计算结果表明决定能否忽略此项分量的关键参数为β=ρg·H/σ0;在理论结果基础上,与Ernst公式比较,得出以下结论:
(1)拉索最大挠度处不在拉索长度中点位置,而是向重力方向有一些偏移。偏移量大小与β值成正比,偏移量与拉索半长比值为:β/6。
(2)拉索最大挠度值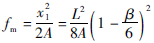 ,与拉索直线长度的二次方成正比,与拉索应力/拉索重度比成反比,与Ernst公式结果比值为(1-β/6)2。
,与拉索直线长度的二次方成正比,与拉索应力/拉索重度比成反比,与Ernst公式结果比值为(1-β/6)2。
(3)拉索的伸长量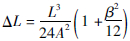 ,与拉索直线长度的三次方成正比,与拉索应力/拉索重度比平方成反比,与Ernst 公式结果比值为:1+β2/12。
,与拉索直线长度的三次方成正比,与拉索应力/拉索重度比平方成反比,与Ernst 公式结果比值为:1+β2/12。
| [1] | ACAMPORA A, MACDONALD J H G, GEORGAKIS C T, et al. Identification of Aeroelastic Forces and Static Drag Coefficients of a Twin Cable Bridge Stay from Full-scale Ambient Vibration Measurements[J]. |
| [2] | ACAMPORA A, MACDONALD J H G, GEORGAKIS C T, et al. Identification of Aeroelastic Forces and Static Drag Coefficients of a Twin Cable Bridge Stay from full-Scale Ambient Vibration Measurements[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2014,124(1):90-98. |
| [3] | HU L, XU Y, HUANG W. Typhoon-induced Non-Stationary Buffeting Response of Long-Span Bridges in Complex Terrain[J]. Engineering Structures, 2013,57(4):406-415. |
| [4] | 张兴标, 沈锐利, 唐茂林,等. 悬索桥锚跨索股索力的精确计算与调整方法[J]. 西南交通大学学报, 2012,47(4):551-559. ZHANG Xing-biao, SHEN Rui-li, TANG Mao-lin,et al. Accurate Calculation and Adjustment Methods for Cable Forces of Anchor-Span Strands for Suspension Bridges[J]. Journal of Southwest Jiaotong University, 2012,47(4):551-559. |
| [5] | 刘志军, 芮筱亭, 王国平,等. 考虑垂度效应的索力振动测量的传递矩阵法[J]. 南京理工大学学报, 2013,37(4):608-615. LIU Zhi-jun, RUI Xiao-ting, WANG Guo-ping,et al. Transfer Matrix Method for Vibration Measurement of Cable Tension Considering Sag[J]. Journal of Nanjing University of Science and Technology, 2013,37(4):608-615. |
| [6] | 王荣辉, 薛礼建. 矮塔斜拉桥索力测试方法研究[J]. 中外公路, 2011,31(2):116-123. WANG Rong-hui, XUE Li-jian. Research on Test Method of Cable Force of Low Pylon Cable-stayed Bridge[J]. Journal of China & Foreign Highway, 2011,31(2):116-123. |
| [7] | 李平利. 大跨度斜拉桥施工阶段几何非线性静力分析[D]. 成都:西南交通大学, 2004. LI Ping-li. Geometric Nonlinear Static Analysis of Long-span Cable-stayed Bridge at Construction Stage[D]. Chengdu:Southwest Jiaotong University, 2004. |
| [8] | 许立强. 确定斜拉桥合理成桥索力的综合方法与施工控制研究[D]. 武汉:武汉理工大学, 2007. XU Li-qiang. Study of Comprehensive Method for Determining Reasonable Cable Force of Cable-stayed Bridge and Construction Control[D]. Wuhan:Wuhan University of Technology, 2007. |
| [9] | AHMAD J, CHENG S. Effect of Cross-Link Stiffness on the In-Plane Free Vibration Behaviour of a Two-Cable Network[J]. Engineering Structures, 2013,52(9):570-580. |
| [10] | ANISTOROAIEI C, HEYMEL U, JUNG R, et al. A Cable Stayed Bridge with Parallel Strand Cables:Elbe Bridge Schnebeck(Germany)-Detailed Design(part 2)[J]. |
| [11] | CHENG B, WANG J, LI C. Compression Behavior of Perforated Plates in Steel Tower Anchorage Zones of Cable-Stayed Bridges[J]. Journal of Constructional Steel Research, 2013,90(5):72-84. |
| [12] | 陈政清. 斜拉索风雨振现场观测与振动控制[J]. 建筑科学与工程学报, 2005,22(4):5-10. CHEN Zheng-qing. On-site Observation of Wind-rain Induced Vibration of Stay Cables and Its Control[J]. Journal of Architecture and Civil Engineering, 2005,22(4):5-10. |
| [13] | 谷音, 钟华, 卓卫东. 基于性能的矮塔斜拉桥结构地震易损性分析[J]. 土木工程学报, 2012,45(增1):218-222. GU Yin, ZHONG Hua, ZHUO Wei-dong. Lower-tower Cable-Stayed Bridge Seismic Vulnerability Analysis[J]. China Civil Engineering Journal, 2012,45(S1):218-222. |
| [14] | 胡传超. 矮塔斜拉桥斜拉索施工工艺及应用[J]. 西部探矿工程, 2008,24(4):204-209. HU Chuan-chao. Stayed Cable Construction Technology and Application of Low Pylon Cable-stayed Bridge[J]. West Mining Engineering, 2008,24(4):204-209. |
| [15] | RAHEEM S E A, HAYASHIKAWA T. Energy Dissipation System for Earthquake Protection of Cable-stayed Bridge Towers[J]. |
| [16] | RAHEEM S E A, HAYASHIKAWA T. Energy Dissipation System for Earthquake Protection of Cable-Stayed Bridge Towers[J]. |
| [17] | 郭致星, 鲁束, 陈清美. 悬链线与抛物线的区别[C]//全国第十一次光纤通信暨第十二届集成光学学术会议.南京:南京邮电学院, 2003. GUO Zhi-xing, LU Shu, CHEN Qing-mei. Difference of Catenary Curve and Parabola Curve[C]//Eleventh National Optical Fiber Communication and Twelfth Integrated Optical Academic Conference. Nanjing:Nangjing University of Posts and Telecommunica-tions, 2003. |
 2016, Vol. 33
2016, Vol. 33