扩展功能
文章信息
- 李红启, 常馨玉, 朱晓宁, 卢越
- LI Hong-Qi, CHANG Xin-Yu, ZHU Xiao-Ning, LU Yue
- 城际干线甩挂运输的公路牵引车调度问题及其求解
- Intercity Line-haul Tractor Dispatching Problem in Trailer Pick-up Transport and Its Solving Method
- 公路交通科技, 2016, Vol. 31 (2): 151-158
- Journal of Highway and Transportation Research and Denelopment, 2016, Vol. 31 (2): 151-158
- 10.3969/j.issn.1002-0268.2016.02.023
-
文章历史
- 收稿日期: 2014-07-18
2. 北京交通大学 交通运输学院, 北京 100044;
3. 北京华运交通咨询开发公司, 北京 100038
2. School of Traffic and Transportation, Beijing Jiaotong University, Beijing 100044, China;
3. Beijing Huayun Traffic Consulting and Development Corporation, Beijing 100038, China
甩挂运输被广泛应用于道路运输领域,其本质上是一种基于道路货运车辆调度的货运运力资源配置模式[1]。经济发达国家在20世纪60年代就已盛行汽车列车甩挂运输,该运输组织形式被推广应用于城际干线运输、城市配送以及多式联运领域。国外甩挂运输所用的汽车列车组合方式多种多样,如:卡车拖挂全挂车、牵引车拖挂半挂车、牵引车拖挂半挂车与全挂车等。我国甩挂运输的发展相对滞后、且目前只允许企业使用牵引车拖挂半挂车开展甩挂运输。自2009年交通运输部等部委联合发布《关于促进甩挂运输发展的通知》以来,物流运输企业开展甩挂运输不仅在体制上面临的制约越来越少,而且可以获得多种扶持。
由于可用车型多样,国外甩挂运输模式广泛应用于城际干线运输和城市配送等领域。现阶段我国企业能够用于开展甩挂运输的车型特点决定了城际干线运输是甩挂运输模式的主要应用领域。城际干线运输以网络化、规模化特征成为体现甩挂运输技术经济优势的依托条件,且城际干线运输的货物交流量大、运距长,便于实现甩挂运输货源组织的规模化,这有利于发挥甩挂运输的整车运输优势。对于物流运输企业而言,在货源组织和车辆装备条件都得以保证时,干线甩挂运输组织工作的重点就是甩挂运输车辆调度。
企业在由传统卡车运输模式向甩挂运输模式转变过程中,需要将其面向单体卡车的调度方式转变为面向汽车列车的调度模式。同单体卡车相比,汽车列车的动力部分和载货部分可自由分离与结合,这就增加了甩挂运输车辆调度工作的复杂性。从调度作业对象看,甩挂运输车辆调度包括牵引车调度、载货半挂车调度、空半挂车调度和汽车列车调度等。企业实践中的甩挂运输车辆调度往往是综合化的调度问题,即上述车辆调度类型的组合形式。
本文定位于牵引车调度这一甩挂运输车辆调度工作中最为核心的问题,建立公路牵引车调度问题数学模型,设计求解算法,并开展牵引车调度问题实践算例的求解与分析。
1 既有研究概述相对于卡车,汽车列车能够通过动力部分和载货部分的自由分离和结合开展甩挂运输,从而获得更高的车辆使用效率[2, 3]。学术界普遍认为汽车列车的调度问题很复杂,是NP难题,部分学者认为传统车辆调度问题(Vehicle Routing Problem,VRP)只是汽车列车调度问题的一个特例[4]。迄今国内外学术界在该类问题方面的研究成果主要体现为3类(其基本特征对比见表 1):
| 对比项 | VRP问题 | TTRP问题 | RRVRP问题 | TSRP问题 |
| 所用车辆 | 单体卡车 | 卡车+全挂车 | 牵引车+半挂车 | 牵引车+半挂车 |
| 网络节点 | 中心场站和客户点 | 中心场站、卡车客户点和汽车列车客户点 | 中心场站和客户点 | 中心场站和半挂车集散点 |
| 运输需求 | 零担 | 零担 | 整车 | 整车 |
| 服务领域 | 短途配送 | 短途配送、小区域运输 | 城市垃圾回收 | 城际干线、小区域运输 |
| 客户点间的货运需求 | 无 | 无 | 无 | 有 |
| 路径长度 | 无限制 | 无限制 | 有限制 | 有限制 |
(1)对于卡车与全挂车组合而成的汽车列车调度问题,有关研究一般称其为TTRP问题(Truck and Trailer Routing Problem)。TTRP问题可叙述为:一些客户点既可以由汽车列车服务,也可以由单独的卡车服务,而有些客户点仅能由卡车提供货运服务;设定卡车和挂车数量已知、路径上客户点的运量满足车辆载运能力约束;求解目标是寻找成本最低的车辆路径集,路径是闭合的,每个客户点都只被提供1次货运服务。TTRP问题的研究成果以文献[4, 5]等为代表。
(2)迄今学术界针对牵引车和半挂车组合的调度问题的研究工作主要体现为RRVRP问题(Rollon-rolloff Vehicle Routing Problem)。RRVRP问题源于城市垃圾运输活动,垃圾运输车将空车厢送到垃圾收集点,车厢装满垃圾后,由垃圾运输车将重车厢运到垃圾集中处理站进行卸车和后续处理。垃圾运输车的作业方式与牵引车加半挂车的汽车列车作业方式类似。该问题的研究成果以文献[6, 7]等为代表。
(3)另一类针对牵引车和半挂车组合的优化运用问题被称为TSRP问题(Tractor and Semi-trailer Routing Problem)。迄今学术界针对TSRP问题的研究背景主要有两种:短途(配送)运输和中长途(干线)运输。TSRP问题的短途运输应用背景包括厂内运输、局部性运输,如:梁波[8]研究了以大型钢铁企业内部物资运输为背景的TSRP问题;范宁宁[9]建立了以集疏运运营成本最小化为目标的数学模型来研究烟大滚装甩挂牵引车调度问题;张磊磊[10]以LPG炼油厂为牵引车场站、将牵引车加半挂车的汽车列车应用于LPG运输。鉴于该类汽车列车从事运输活动的规模经济优势,TSRP问题的干线运输应用前景更被看好。城际干线运输网络的几乎所有节点间均可能存在货运需求,这种节点间的运输需求呈现为“多对多”的关系,与VRP问题的节点间运输需求“一对多”的关系[11]明显不同。H. Li等[12, 13]在城际干线运输网络上界定出TSRP问题。
2 数学模型与算例设计 2.1 问题特点与数学模型区别于既有研究工作所提出的TTRP问题和RRVRP问题,本文瞄准物流运输企业运用汽车列车进行甩挂运输过程中所面对的牵引车调度这一核心问题,提出城际干线运输中的牵引车调度问题(Line-haul Tractor Dispatching Problem,LTDP)。LTDP问题有以下基本特点:
(1)整车运输
甩挂运输的基本优势来源于牵引车和半挂车之间可用很短时间进行分离和结合作业,这便于以整个半挂车及其所载货物作为装卸和中转单元,从而大大压缩牵引车在场站内因等待装卸作业所需的停留时间。LTDP问题可以以半挂车为运输作业单位。
(2)“多对多”问题
运输网络由节点V(包括1个中心场站v0和n个半挂车集散点vi(i=1,2,…,n))和边A(A={(i,j)|i≠j,i,j=0,1,2,…,n})组成。中心场站是指可以存放大量牵引车、规模较大、在运输网络中处于枢纽地位的场站;半挂车集散点是指需要货运服务并进行半挂车甩挂作业的节点,其运输需求和保有的半挂车数量均不同。
LTDP问题的运输需求与传统VRP问题的最大区别在于LTDP问题考虑了半挂车集散点之间的货运需求,使问题变为“多对多”特征,货运需求变为货物交流矩阵形式。不妨将货运需求分为3类:由中心场站v0发往半挂车集散点vi(vj)的货运量记为d=(r01,r02,…,r0n),由vi(vj)发往v0的货运量记为p=(r10,r20,…,rn0),n个半挂车集散点两两之间的货物流量记为矩阵B,其中rij表示任意两个半挂车集散点间的货运需求,以半挂车为运输单位,则货
物流量矩阵 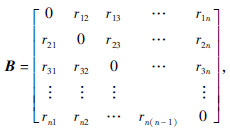 ,货运需求可表示为矩阵形式:
,货运需求可表示为矩阵形式: 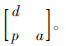 。
。
(3)驾驶员与牵引车连续工作时间
在甩挂运输模式中,牵引车的利用率是焦点,而牵引车连续工作时间与驾驶员工作时间之间联系密切。由于人体持续工作耐力、车辆行驶过程安全要求等因素,驾驶员的法定工作时间是有硬性要求的,如在美国,卡车驾驶员连续行车时间不能超过10 h,在充分休息8 h的条件下,可在岗15 h(包括用于等待货物装卸、车辆维修保养等的停留时间)[14]。牵引车连续工作时间极大影响着LTDP问题路径方案的路径长度。
(4)考虑甩挂运输节能减排效果的目标函数
甩挂运输竞争优势的发挥依赖于车辆装备和组织管理技术,在相应的市场条件和软硬件装备条件下,甩挂运输的技术经济特点得以发挥,由此带来的效果是道路货运效率的提升,这意味着以更少的投入获得更多的产出。道路货运的投入因素体现为固定成本投入和变动成本投入,其中油耗量是占比较大的一种变动成本;道路货运的产出因素体现为道路货运活动所实现的货物周转量。为同时表征甩挂运输车辆调度模式的运输效率和节能减排效果,选取“吨公里CO2排放量”作为目标函数。该指标越高,说明道路货运的效率越低,节能减排效果越差。
与VRP问题和TTRP问题目标函数通常采用的总运距或变动成本等规模类指标不同,吨公里CO2排放量是表征货运行业CO2排放效果的基本指标[15],属于效率类指标。在我国甩挂运输试点工作中,各企业甩挂运输试点方案的评价指标之一就是CO2排放量,本文选用该指标可使研究结果尽可能贴近我国甩挂运输企业实践。此外,该指标是一种相对指标,便于进行不同算例计算结果的横向比较。
LTDP问题数学模型涉及两类决策变量:Xijkl表示编号为k的牵引车在弧(i,j)上拖挂行驶的次数,为0到dmax间的整数;Xijkt表示编号为k的牵引车在弧(i,j)上独自行驶的次数,为0到dmax间的整数,其中dmax为货运需求的最大值。
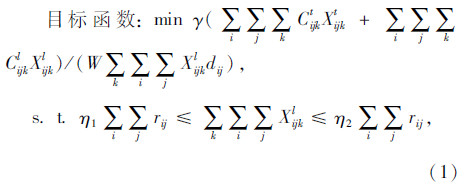
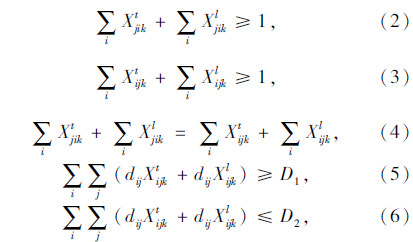
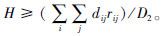 。γ为依据联合国政府间气候变化专门委员会提供的CO2排放量计算方法所使用的排放系数;Cijkt与Cijkl分别为第k台牵引车独自行驶或拖挂半挂车行驶于vi与vj间的燃油消耗量;W为半挂车载货量;设牵引车行驶速度恒定,则网络节点间运距和行驶时间矩阵一致,记dij为vi与vj间的运距;η1,η2分别为满足货运需求上限和下限的比例系数;记牵引车路线的运距范围在D1与D2之间。在牵引车行驶速度确定的情况下,运距范围与驾驶员的工作时间范围一致。
。γ为依据联合国政府间气候变化专门委员会提供的CO2排放量计算方法所使用的排放系数;Cijkt与Cijkl分别为第k台牵引车独自行驶或拖挂半挂车行驶于vi与vj间的燃油消耗量;W为半挂车载货量;设牵引车行驶速度恒定,则网络节点间运距和行驶时间矩阵一致,记dij为vi与vj间的运距;η1,η2分别为满足货运需求上限和下限的比例系数;记牵引车路线的运距范围在D1与D2之间。在牵引车行驶速度确定的情况下,运距范围与驾驶员的工作时间范围一致。
约束条件(1)要求货运需求满足率处于一定范围内,约束条件(2)~(4)确保路径闭合与度平衡,约束条件(5)与(6)为路径长度约束。
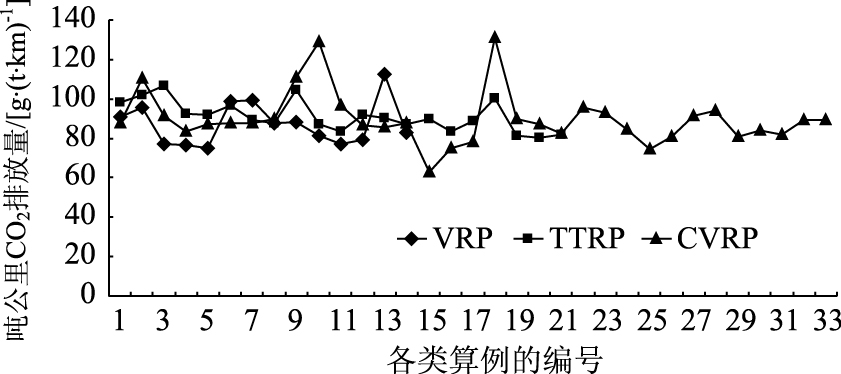
2.2 算例既有相关研究工作提供了若干基准算例及其最优解,本文依据目前可获得的这些算例的最优方案,估算最优方案下各个算例的吨公里CO2排放量。采用以下基准算例作为参考:(1)Christofides等[16]提供的14个VRP问题基准算例。(2)Fisher等[17]提供的6个有容量约束的车辆调度问题(Capacitated Vehicle Routing Problem,CVRP)问题基准算例,Christofides 等[18]提供的13个CVRP基准算例,Russell等[19]提供的4个CVRP问题基准算例,以及Christofides等[16]提供的4个CVRP问题基准算例,共27个CVRP问题基准算例。由于不同学者采用不同求解方法所获得的某基准算例的最优解不同,某基准算例可能有多个估算结果(图 1给出了33个估算结果)。(3)Chao[4]提供的21个TTRP问题基准算例。值得注意的是,上述基准算例一般采用总运距作为目标函数,所以其最优方案极有可能与以吨公里CO2排放量为目标函数的最优方案有明显不同。从估算结果看(图 1),上述算例最优方案的吨公里CO2排放量主要分布在60~140 g/(t·km)之间,且其平均值较为接近。此外,上述算例最优方案的总运距波动范围则在100~1 900 km之间。可见,以总运距作为对比指标时不适宜各类算例求解结果之间的横向比较。
|
| 图 1 既有相关研究中各类基准算例最优解的吨公里CO2排放量估计 Fig. 1 Estimation of CO2 emissions per ton kilometer of different benchmark instances in existing related researches 注:各类算例的编号是本文拟定的,每个编号的算例对应于本文所采用的某基准算例。 |
能够确定城市节点间货运需求量是设计LTDP问题实践算例的基本条件。本文参照文献[20]提供的城际干线运量估算数据,以山东省17个地级城市为网络节点,以高速公路为网络的边,抽象设计若干LTDP问题实践算例。在这些算例中,以17个地市中的某城市作为中心场站、其他16个地市作为客户点,可得到17个不同的算例,这些算例的不同求解结果也反映了不同城市作为中心场站的优势。根据这些地市之间的货物交流量,设定某一开展甩挂运输业务的企业市场占有率,合理拟定半挂车额定载重及其实载率,可确定山东省城际干线甩挂运输网络每天需满足的以半挂车数为单位的货物交流需求。表 2为本文所用算例的山东省地市节点间的载货半挂车交流量。
| (单位:veh) | |||||||||
| (unit: veh) | |||||||||
| 济南 | 青岛 | 淄博 | 枣庄 | 东营 | 烟台 | 潍坊 | 济宁 | 泰安 | |
| 济南 | 0 | 1 | 2 | 1 | 2 | 1 | 3 | 1 | 0 |
| 青岛 | 1 | 0 | 6 | 0 | 4 | 7 | 18 | 0 | 1 |
| 淄博 | 1 | 4 | 0 | 1 | 2 | 2 | 3 | 1 | 1 |
| 枣庄 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| 东营 | 2 | 3 | 2 | 0 | 0 | 1 | 1 | 0 | 1 |
| 烟台 | 1 | 6 | 2 | 0 | 2 | 0 | 5 | 0 | 0 |
| 潍坊 | 3 | 15 | 3 | 0 | 1 | 4 | 0 | 1 | 2 |
| 济宁 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 泰安 | 0 | 1 | 1 | 1 | 1 | 0 | 2 | 0 | 0 |
| 威海 | 0 | 2 | 1 | 0 | 1 | 1 | 1 | 0 | 0 |
| 日照 | 0 | 3 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| 莱芜 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 |
| 临沂 | 1 | 2 | 3 | 0 | 1 | 1 | 2 | 1 | 2 |
| 德州 | 0 | 0 | 3 | 0 | 1 | 0 | 1 | 1 | 2 |
| 聊城 | 1 | 1 | 4 | 0 | 1 | 0 | 1 | 2 | 3 |
| 滨州 | 2 | 1 | 0 | 0 | 1 | 0 | 4 | 0 | 1 |
| 菏泽 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| 威海 | 日照 | 莱芜 | 临沂 | 德州 | 聊城 | 滨州 | 菏泽 | ||
| 济南 | 0 | 0 | 0 | 1 | 0 | 1 | 2 | 1 | |
| 青岛 | 3 | 3 | 1 | 2 | 1 | 1 | 1 | 0 | |
| 淄博 | 1 | 0 | 0 | 3 | 3 | 3 | 0 | 1 | |
| 枣庄 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 东营 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | |
| 烟台 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | |
| 潍坊 | 1 | 1 | 1 | 2 | 1 | 1 | 4 | 0 | |
| 济宁 | 0 | 0 | 0 | 1 | 1 | 2 | 0 | 0 | |
| 泰安 | 0 | 0 | 0 | 2 | 2 | 3 | 1 | 1 | |
| 威海 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 日照 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 莱芜 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | |
| 临沂 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | |
| 德州 | 0 | 0 | 0 | 0 | 0 | 2 | 1 | 0 | |
| 聊城 | 0 | 0 | 1 | 0 | 2 | 0 | 1 | 1 | |
| 滨州 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | |
| 菏泽 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | |
借鉴既有VRP和TTRP问题求解算法的研究成果,采用模拟退火(SA)算法求解LTRP问题,SA算法被既有研究工作证明是可以成功解决汽车列车调度问题的一类启发式算法[6, 21]。
3.1 算法主流程LTDP问题数学模型的约束条件(5)与(6)为构造可行的牵引车运行路线的基本依据。在对算例进行试算时,采用“牵引车数量=货运需求总量/a”,式中a为经验值。在重复SA优化过程中增加牵引车数,使得货运需求满足率持续提高,可确定合适的牵引车数。
牵引车数量是求解LTDP问题SA算法的首要参数,求解结果与牵引车数量有很大关系。牵引车数量的确定方法包含最优牵引车数量Mbest的确定和最 优牵引车路线方案的确定,以下是牵引车数量Mbest的算法求解基本流程。
Step 1: 取初始牵引车数量为经验值M=D/a(式中D为货运需求总量;a为经验值)。
Step 2: 根据牵引车运行路线的总运距约束构造可行的牵引车路线集合V,随机选取M条牵引车路线作为初始解X。
Step 3: 设定初温T=T0;外循环计数变量w=0,内循环计数变量q=0;货运满足率设定为解X的货运需求满足率Rbest=RX。
Step 4: 外循环计数w=w+1。
Step 5: 内循环计数q=q+1。
Step 6: 从V中随机选取1条牵引车路线,替换X中随机1条牵引车路线,生成新的解Z。
Step 7: Metropolis准则判定(k为步长参数)。
根据Metropolis准则第1个判定条件,比较路线方案X和Z的货运需求满足率,若Δ=R(Z)-R(X)≥0,则将X替换为Z,即X=Z;若R(z)-R(X)<0,进入Metropolis准则的第2个判定条件,设r为0至1之间的随机数,若exp(Δ×k/T)>r,则将X替换为为Z,即X=Z。
Step 8: 计算当前解Xbest下的Rbest,Xbest=X,Rbest=RX。
Step 9: 内循环终止判定。
内循环终止准则要求达到设定的内循环次数。若在等温下q达到内循环次数Ne,即q=Ne,则进入下一次外循环,T计数,q置零,即T=T×k,q=0;若q<Ne,回到Step 5。
Step 10: 外循环终止判定。
外循环终止准则要求达到外循环末温。若外循环未达到终止温度TF,即T-TF>0,回到Step 4;若T-TF≤0,终止SA算法外循环过程。
Step 11: 设R1,R2为拟达到的货运需求满足率边界。若货运需求满足率Rbest<R1,则使M=M+1,回到Step 2;若货运需求满足率Rbest>R2,则使M=M-1,回到Step 2;若货运需求满足率R1≤Rbest≤R2,则得到最优牵引车数量Mbest,Mbest=M。
在牵引车数量Mbest确定后,可以以Mbest为已知量进行牵引车路线方案的求解,牵引车路线方案的算法求解流程总体上与牵引车数量求解流程一致,只是在Step 1直接取牵引车数为Mbest;此外,外循环终止判定环节增加另外一种准则:若外循环获得高于R2的货运需求满足率和低于第2.1节所建模型的目标函数值Cbest,则回到Step 4;否则,终止SA算法外循环过程。
3.2 后处理后处理过程针对SA算法求解所得的满意解,该过程是可选的,对特定算例满意解有较好的再优化效果。后处理包括两方面,一是删除空驶路段,二是对路段进行重新整合使其满足路径长度约束,具体步骤如下:(1)考察满意方案中每条路线的路段是否为牵引车独自行驶路段,将那些所包含的路段全部为这种路段的路线直接从方案中删除;(2)考察满意方案中每条路线的路段是否为这种路段,找出其所包含的路段中除了一段有普通货运,其他路段全部为牵引车独自行驶路段的路线;(3) 若将第(2)步中找出的路线删除,则为了保证需求满足率,必须把拟删除的这些路线中有普通货运的那条路段加到合适的路线上;(4)对经过调整后的最终路线方案进行统计,更新统计指标。
4 算例求解在本文所构建的LTDP问题数学模型中,驾驶员与牵引车连续工作时间是牵引车路径优化过程的重要约束因素,这必然将模型解的可行域大大压缩。货运需求满足率可能会因货运需求分布、中心场站分布等的不同而难以达到100%。为确保获得不同算例的满意解,本文在对山东省城际干线甩挂运输网络算例进行求解时,将货运需求满足率分别设定为85%和100%两种情况。选取一汽集团生产的平头柴油半挂牵引车(型号CA4250P66K24T1A1HE)和山东鲁峰专用汽车公司生产的两轴厢式运输半挂车(型号ST9351XXY)。根据交通运输部发布的《道路运输车辆燃料消耗量达标车型表》的有关信息,当车辆行驶速度定为50 km/h时,牵引车拖挂半挂车行驶的油耗取为32 L/(100 km),牵引车独自行驶的油耗取为18 L/(100 km)。
在山东省17个地市中,有6个地市作为中心场站时可以达到100%的货运需求满足率,这些城市包括:济南、青岛、淄博、潍坊、泰安、莱芜。总体看,这几个地市是交通区位较优、货源规模较大的城市。将货运需求满足率设为85%(在LTDP问题模型中取η1=85%,η2=86%),则对17个算例的求解结果如表 3所示。
| 中心场站位置 | 济南 | 青岛 | 淄博 | 枣庄 | 东营 | 烟台 |
| 货运需求满足率/% | 85 | 85 | 85 | 85 | 85 | 85 |
| 牵引车数/veh | 62 | 54 | 54 | 86 | 61 | 100 |
| 总油耗/L | 18 831 | 17 746 | 17 418 | 23 789 | 18 471 | 27 475 |
| 货物周转量/(t·km) | 756 318 | 764 676 | 757 026 | 730 140 | 739 671 | 770 496 |
| 吨公里CO2排放量/[g·(t·km)-1] | 67.97 | 63.35 | 62.81 | 88.95 | 68.17 | 97.35 |
| 牵引车平均运输的挂车数/veh | 4.29 | 4.93 | 4.93 | 3.09 | 4.36 | 2.66 |
| 中心场站位置 | 潍坊 | 济宁 | 泰安 | 威海 | 日照 | 莱芜 |
| 货运需求满足率/% | 85 | 85 | 85 | 65 | 85 | 85 |
| 牵引车数/veh | 52 | 100 | 64 | 69 | 77 | 64 |
| 总油耗/L | 17 174 | 26 537 | 18 993 | 19 442 | 21 903 | 18 964 |
| 货物周转量/(t·km) | 760 716 | 755 100 | 741 291 | 583 566 | 741 141 | 742 938 |
| 吨公里CO2排放量/[g·(t·km)-1] | 61.63 | 95.94 | 69.95 | 90.95 | 80.68 | 69.68 |
| 牵引车平均运输的挂车数/veh | 5.12 | 2.66 | 4.16 | 3.86 | 3.45 | 4.16 |
| 中心场站位置 | 临沂 | 德州 | 聊城 | 滨州 | 菏泽 | |
| 货运需求满足率/% | 85 | 85 | 85 | 85 | 75 | |
| 牵引车数/veh | 69 | 78 | 76 | 60 | 94 | |
| 总油耗/L | 20 275 | 22 409 | 21 820 | 18 252 | 25 295 | |
| 货物周转量(t·km) | 735 831 | 760 380 | 753 075 | 738 381 | 638 790 | |
| 吨公里CO2排放量/[g·(t·km)-1] | 75.22 | 80.46 | 79.10 | 67.48 | 108.10 | |
| 牵引车平均运输的挂车数/veh | 3.86 | 3.41 | 3.50 | 4.43 | 2.83 |
除了以威海、菏泽为中心场站的算例外,其他算例的货运需求满足率均达到了85%,吨公里CO2排放量的平均值为78.11 g/(t·km)。
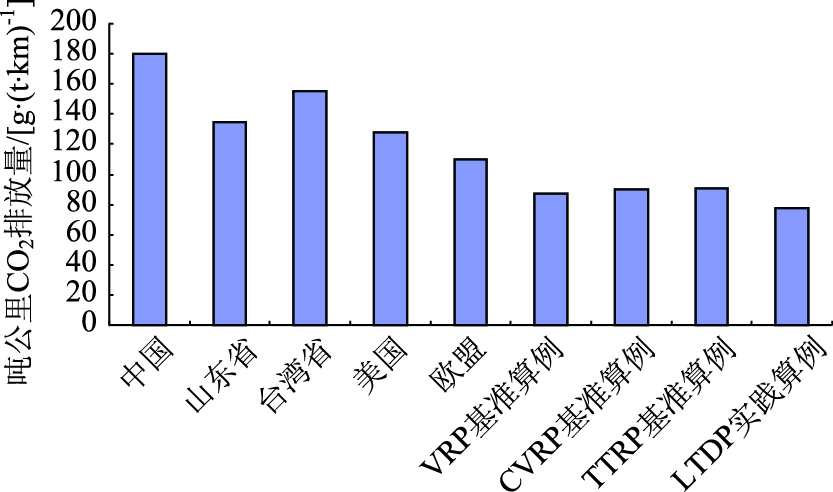
参考既有相关研究结论,比较全国、山东省、台湾省、美国、欧盟等国家和地区道路货运吨公里CO2排放量的平均水平,以及由本文2.2节选定的既有基准算例以总运距为目标函数的最优解的吨公里CO2排放量(图 2)。可见,理论研究层面的算例优化计算结果优于实践。相对于VRP,CVRP,TTRP问题基准算例,本文算例的求解效果更好一些。原因是在基于城际干线运输过程的公路牵引车调度求解算例中,干线运输车辆吨位较大且运距较长,规模经济效应明显。
由上述算例运算工作,有以下3点值得注意:
(1)由于每个工作日内牵引车连续工作总时间决定了牵引车路径的合理长度区间,城际干线甩挂运输网络上中心场站的位置、货运需求的空间分布等因素对牵引车调度方案设计具有重要的影响,应科学权衡货运服务水平(货运需求满足率水平)和牵引车工作时间利用之间的关系。另一方面,本文的算例求解结果在一定程度上表明了中心场站选址与牵引车调度之间的密切关系,可考虑将牵引车调度方案和牵引车场站选址有机结合。
(2)在甩挂运输模式下,每条牵引车路线上拖挂半挂车的数量是重要参数之一,在一定程度上可表征运输网络上牵引车的使用效果。本文的算例求解工作表明,每条牵引车路线上拖挂半挂车约为4台;求解效果越好的算例,每条牵引车路线能拖挂的半挂车数量越多一些。企业应尽可能采取措施提高每条路线上拖挂半挂车的数量。
(3)牵引车的驾驶员配备方式对于牵引车连续工作时间具有直接影响,这也决定了牵引车调度方案的形式。城际干线运输网络可能处于城市群,也可能处于较大地理空间范围内,这就使运距参差不一。当驾驶员乘组包括2名及以上驾驶员时,每台牵引车可以服务于更多的半挂车集散点,承担更多的运输需求,也可减少牵引车的保有和使用总量。
5 结论现阶段我国企业能够用于开展甩挂运输的车型为牵引车拖挂半挂车,这决定了城际干线运输是当前我国发展甩挂运输模式的主要应用领域。结合当前我国有关企业的甩挂运输试点实践,本文提出了以货运吨公里CO2排放量为目标函数的LTDP问题,该类问题面向“多对多”式的城际整车运输需求,尊重驾驶员工作时间和牵引车连续工作时间等实践要求。针对LTDP问题的整数规划模型,设计了基于模拟退火的求解算法主流程,并辅以可选用的、针对主流程运算结果的后处理操作。算例表明,本文所构建的LTDP问题整数规划模型及其启发式求解方法是可行的。现阶段我国甩挂运输试点企业往往在原有单体卡车运输线路的基础上将其改造为甩挂运输线路,较多采用的甩挂运输形式是“一线两点,两端甩挂”。从本文经过求解获得的牵引车路线方案看,较为理想的牵引车路线往往是若干“一线两点,两端甩挂”模式的组合,这种组合过程很复杂。在较大规模的城际干线运输网络中开展甩挂运输,一般难以用传统的、人工调度方式确定牵引车调度方案,应考虑借助运筹优化技术。
| [1] | 李红启,高洪涛.甩挂运输操作技术与方法[M].北京:中国物资出版社,2012.LI Hong-qi,GAO Hong-tao.Operational Technology and Method of Tractor and Semitrailer Transportation[M].Beijing:China Logistics Press,2012. |
| [2] | SEMET F,TAILLARD E.Solving Real-life Vehicle Routing Problems Efficiently Using Tabu Search[J]. |
| [3] | 李亚茹.提高道路运输效率的有效途径:甩挂运输[J].公路交通科技,2004,21(4):119-122.LI Ya-ru.Semi-trailer Swap Transport:An Effective Way to Improve Road Transport Efficiency[J].Journal of Highway and Transportation Research and Development,2004,21(4):119-122. |
| [4] | CHAO I M.A Tabu Search Method for the Truck and Trailer Routing Problem[J]. |
| [5] | VILLEGAS J G,PRINS C,PRODHON C,et al.A Matheuristic for the Truck and Trailer Routing Problem[J]. |
| [6] | BODIN L,MINGOZZI A,BALDACCI R,et al.The Rollon-rolloff Vehicle Routing Problem[J]. |
| [7] | BALDACCI R,BODIN L,MINGOZZI A.The Multiple Disposal Facilities and Multiple Inventory Locations Rollon-rolloff Vehicle Routing Problem[J]. |
| [8] | 梁波.大型钢铁企业厂内车辆循环甩挂运输模式研究[D].长沙:中南大学,2009.LIANG Bo.Research on Semi-trailer Loop Swap Transportation Applied in Large-scale Iron and Steel Works[D].Changsha:Central South University,2009. |
| [9] | 范宁宁.烟大滚装甩挂运输牵引车调度优化研究[D].大连:大连海事大学,2012.FAN Ning-ning.Research on Tractor Optimization Scheduling of Ro-Ro Left-hanging Transportation from Yantai to Dalian[D].Dalian:Dalian Martime University,2012. |
| [10] | 张磊磊.LPG循环甩挂运输调度优化研究[D].大连:大连海事大学,2013.ZHANG Lei-lei.Research on LPG Cycle Drop and Pull Transport Optimization Scheduling[D].Dalian:Dalian Martime University,2013. |
| [11] | BARCOS L,RODRÍGUEZ V,ÁLVAREZ M J,et al.Routing Design for Less-than-truckload Motor Carriers Using Ant Colony Optimization[J]. |
| [12] | LI H,LI Y,ZHAO Q,et al.The Tractor and Semitrailer Routing Considering Carbon Dioxide Emissions[J/OL].Mathematical Problems in Engineering,2013,Article ID 509160,1-12[2015-09-10] |
| [13] | LI H,LI Y,LU Y,et al.The Effects of the Tractor and Semitrailer Routing Problem on Mitigation of Carbon Dioxide Emissions[J/OL].Discrete Dynamics in Nature & Society,2013,Article ID 80935,1-414[2015-09-10]. |
| [14] | HERTZ R P.Hours of Service Violations among Tractor-trailer Drivers[J]. |
| [15] | IERLAND E V,GRAVELAND C,HUIBERTS R.An Environmental Economic Analysis of the New rail Link to European Main Port Rotterdam[J]. |
| [16] | CHRISTOFIDES N,MINGOZZI A,TOTH P.The Vehicle Routing Problem[M]//CHRISTOFIDES N,MINGOZZI A,TOTH P,et al.Combinatorial Optimiza-tion.London:John Wiley and Sons,1979. |
| [17] | FISHER M L.Optimal Solution of Vehicle Routing Problems Using Minimum K-trees[J]. |
| [18] | CHRISTOFIDES N,EILON S.An Algorithm for the Vehicle-dispatching Problem[J]. |
| [19] | RUSSELL R,IGO W.An Assignment Routing Problem[J]. |
| [20] | 高洪涛,李红启.道路甩挂运输组织技术及其应用实践[M].北京:中国物资出版社,2011.GAO Hong-tao,LI Hong-qi.Operational Method and Application of Tractor and Semitrailer Transportation[M].Beijing:China Logistics Press,2011. |
| [21] | LIN S W,YU V F,CHOU S Y.A Note on the Truck and Trailer Routing Problem[J]. |
| [22] | 李红启.山东省甩挂运输发展规划研究[R].北京:北京航空航天大学,2013.LI Hong-qi.Research on Developing Plan of Tractor and Semitrailer Transportation in Shandong Province[R].Beijing:Beihang University,2013. |
| [23] | LIAO C H,TSENG P H,LU C S.Comparing Carbon Dioxide Emissions of Trucking and Intermodal Container Transport in Taiwan[J]. |
| [24] | DAVIS S C,DIEGEL S W,BOUNDY R G.Transportation Energy Data Book:Edition 32[R].Oak Ridge:Oak Ridge National Laboratory,2011. |
| [25] | European Environment Agency.Transport at a Crossroads-TERM 2008:Indicators Tracking Transport and Environment in the European Union[M].Luxembourg:Office for Official Publications of the European Communities,2009. |
 2016, Vol. 31
2016, Vol. 31