扩展功能
文章信息
- 刘金刚, 刘凯, 熊乐, 李文昌
- LIU Jin-gang, LIU Kai, XIONG Le, LI Wen-chang
- CVT起步离合器智能预测控制技术研究
- Research of Intelligent Prediction Control Technology of CVT Starting Clutch
- 公路交通科技, 2016, Vol. 31 (2): 135-142
- Journal of Highway and Transportation Research and Denelopment, 2016, Vol. 31 (2): 135-142
- 10.3969/j.issn.1002-0268.2016.02.021
-
文章历史
- 收稿日期: 2014-07-11
2. 中国兵器工业集团江麓机电集团有限公司, 湖南 湘潭 411105
2. Jianglu Machinery Group Co., Ltd., China North Industries Group Corporation, Xiangtan Hunan 411105, China
受复杂多变的工况以及离合器控制系统本身等多方面的影响,CVT起步离合器具有明显的时变性和非线性。当油温、占空比变化率等因素发生变化时,传统的机理模型不能准确反映执行机构的真实性能,使得离合器起步控制品质下降。因此,离合器的控制技术是CVT的关键控制技术之一。
在起步离合器控制中,高速开关阀作为先导阀,接收经过处理后的车速、压力、发动机转速等信号产生的脉宽调制(PWM)信号,使离合器控制阀实现对离合器液压缸的控制,从而实现对离合器接合压力的控制。由于阀的充油和泄油过程需要一定的时间,因此执行机构呈现时滞性;由于液压系统存在泄漏,因此高速开关阀存在滞环、死区、饱和区、阻尼、温度影响等非线性因素,使得整个液压执行机构呈现严重的时变性和非线性[1, 2, 3]。
针对离合器的控制,国内外学者做了大量的研究。M. Montanari 等[4]认为合适的模型对于系统仿真研究至关重要,基于简化的液压离合器模型建立了闭环控制系统,对离合器液压伺服机构进行了控制和评价。G. Huron等[5]进行了离合器数值模拟试验,认为车辆起步过程中的振动冲击主要来自摩擦片的滑摩、离合器接合压力的变化等。罗永革等[6]在湿式离合器数学模型的基础上计算了各种工况下离合器的接合压力。刘振军等[7, 8]对离合器的起步和换挡性质进行了分析,设计了模糊控制器并分析了影响换挡品质的因素。
本文利用试验分析方法进行离合器电液控制系统建模,对传统机理模型、支持向量机模型和径向基 (RBF)神经网络模型进行比较分析。基于台架试验数据,建立支持向量机预测模型,并利用该模型代替传统的机理模型,建立无级变速器起步离合器智能预测控制系统,并在不同起步意图下进行仿真和实车试验。
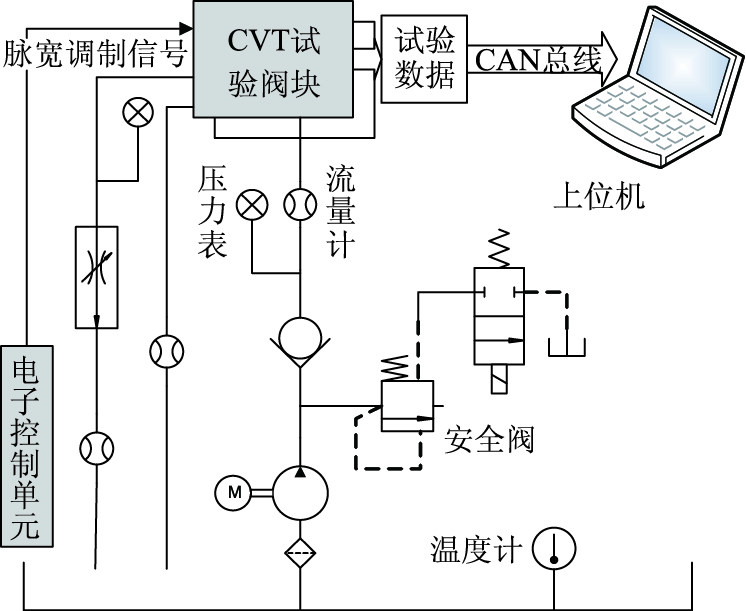
1 建模数据采集 1.1 试验方法在如图 1所示的无级变速器液压控制试验台上进行试验,试验原理如图 2所示。该测试系统采用上、下位机结构,上位机主要完成数据处理和显示,下位机主要完成各类信号的采集及电液执行机构的驱动。试验过程中,由电子控制单元(ECU)发出不同占空比的脉宽调制信号至高速开关阀,在离合器输入口安装相应传感器,ECU将实时占空比和压力等信号通过CAN总线传输至上位机。

|
| 图 1 液压控制模块试验台 Fig. 1 Hydraulic control module test-bed |
|
| 图 2 液压控制模块测试原理 Fig. 2 Principle of hydraulic control module test |
由于油温和占空比变化率是影响离合器控制系统非线性的重要因素,因此分别在不同油温和占空比变化率时进行试验。占空比变化率的变化通过改变单次试验时间来获得,试验时间越短,则占空比变化率越大。占空比变化率表述为占空比由0增加至100%所需的时间,如100/30表示占空比由0增加至100%所需时间为30 s。
分别在不同温度下采集离合器接合压力值,建立如表 1所示的试验方案。
| 试验次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 占空比变化率 | 100/10 | 100/10 | 100/15 | 100/15 | 100/30 | 100/30 | 100/60 | 100/60 | 100/120 | 100/120 | 100/240 |
| 液压油温度/℃ | 36 | 65 | 36 | 65 | 39 | 65 | 39 | 65 | 40 | 65 | 42 |
为了比较温度和占空比变化率对离合器电液控制系统的影响,建立如表 2所示的模型训练与测试方案。
| 数据组 | 训练集 | 测试集 | ||||
| 样本数 | 油温/℃ | 占空比变化率 | 样本数 | 油温/℃ | 占空比变化率 | |
| 1 | 607 | 65 | 100/30 | 13 | 65 | 100/30 |
| 2 | 607 | 65 | 100/30 | 13 | 65 | 100/10 |
| 3 | 607 | 65 | 100/30 | 13 | 39 | 100/30 |
| 4 | 607 | 65 | 100/30 | 13 | 39 | 100/60 |
| 5 | 610 | 39 | 100/30 | 45 | 65 | 100/60 |
| 6 | 409 | 36 | 100/10 | 44 | 36 | 100/15 |
| 7 | 202 | 65 | 100/10 | 45 | 36 | 100/15 |
SVM是由Vapnik提出的一种建立在统计学习理论基础上的新型机器学习算法,能够在很广的各种函数集中构造函数,针对有限样本的情况,得出现有信息下的最优解,具有泛化和学习能力强、能较
好处理小样本和非线性问题等优点,目前已在目标识别、非线性建模与预测、故障诊断等领域得到了成功的应用[9]。根据统计学原理,在非线性系统的黑箱建模过程中,给定训练样本集{xi,yi},i=1,…,n,xi为输入矢量,yi为xi对应的输出,SVM通过映射将数据从低维空间转换到高维空间进行线性回归。根据结构风险最小化原则,优化目标函数为:

最终得到回归方程为:


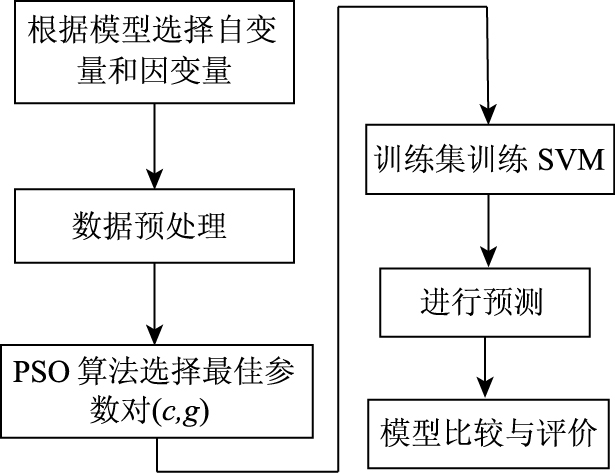
采用表 2所示的模型训练与测试数据,建立基于SVM的离合器控制系统模型所需的训练样本。对于(k+1)时刻的离合器接合压力预测输出值为y (k+1),其对应的输入量由以下部分组成:(1) (k+1)时刻前的离合器的接合压力输出值为y(k),y(k-1),y(k-2); (2) 脉宽调制信号的占空比输入值为τ(k+1),τ(k),τ(k-1),τ(k-2); (3) (k+1)时刻前的占空比变化率为[τ (k+1)-τ (k)]/t,[τ (k)-τ(k-1)]/t,[τ(k-1)-τ(k-2)]/t; (4)液压油温度为T。离合器SVM数学模型建模流程如图 3所示。
|
| 图 3 离合器SVM数学模型建模流程图 Fig. 3 Flowchart of clutch SVM mathematical modeling |
由于惩罚因子和RBF核参数对SVM的泛化能力有着很大程度的影响,因此需合理选取相应参数,以确保测试样本理想的预测准确率。目前,常用的选取SVM参数的方法是交叉验证法和粒子群优化算法(PSO)。由于交叉验证法缺乏坚实的理论基础,且粒子群优化算法具有易实现、效率高等优点,因此本文选取PSO粒子群优化算法对SVM参数对(C,g)进行寻优,将所得均方根误差作为粒子群的目标函数值。粒子按照如下所示的PSO算法核心迭代公式计算得到最优解:

具体算法流程如图 4所示。

|
| 图 4 PSO寻优算法流程图 Fig. 4 Procedure of PSO search algorithm |
表 2中前4组的训练集相同,粒子群算法寻优得出SVM最优参数对(C,g)的值为(3.7,0.01),训练最终得到的离合器模型的支持向量有259个,故其决策函数为:
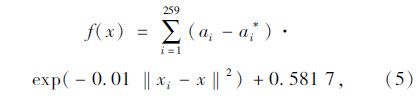
式中 (ai-ai*)为支持向量的系数。
训练得到表 2中第5~7组的最优参数对(C,g)和离合器模型支持向量的个数分别为:(12.5,0.01),152个;(100,0.01),115个;(1,0.062 5),116个。
3 预测模型的性能评价 3.1 基于径向基(RBF)神经网络离合器预测控制模型的建立RBF神经网络模型是一种3层前馈式神经网络,具有逼近能力强和学习速度快等优点,广泛应用于非线性问题的求解[10]。输入层由信号源节点组成,隐含层是对激活函数(格林函数或高斯函数,一般取高斯函数)的参数进行调整,输出层单元对输入模式的作用做出响应。从输入层空间到隐含层空间是以非线性变换的,而从隐含层空间到输出层空间是线性变换的[11],具体结构图如图 5所示。

|
| wlm—权值;Φi—隐含层节点激活函数;其他变量含义同式(6)。 图 5 RBF神经网络结构 Fig. 5 Structure of RBF neural network |
在RBF神经网络中,选用形式简单、径向对称、解析性较好的高斯函数作为隐含层的基函数:

同样采用如表 2所示的训练及预测数据,完成基于RBF神经网络的离合器数学模型的训练。表 2中前4组训练模型相同,选取目标均方误差为0.000 1,扩展速度为1,输入层、隐含层和输出层神经元数分为11,1,30个。同理,表 2中第5~7组数据的目标均方误差取为0.000 1,扩展速度分别为3,3,2;隐含层神经元个数分别为22,16,17个。
3.2 离合器传统机理模型的建立离合器的工作过程简化如图 6所示。

|
| 图 6 离合器接合示意图 Fig. 6 Schematic diagram of clutch engagement |
离合器接合动力学方程为:

机理建模方法是通过学习被控对象的性质,分析找出其内部机理规律,忽略非线性因素,建立具有明确实际物理意义的线性模型。采用机理建模方法,忽略电磁开关阀中存在饱和区、死区及滞环等非线性因素,建立如图 7所示的CVT起步离合器传统机理模型:

|
| 图 7 离合器传统机理模型 Fig. 7 Traditional mechanism model of clutch |
图 7中阀控液压缸的动力学平衡方程为:

得到离合器机理模型控制系统方框图,如图 8所示。

|
| 图 8 离合器机理模型传递函数方框图 Fig. 8 Block diagram of transfer function of clutch mechanism model |
由图 8得到系统传递函数为:
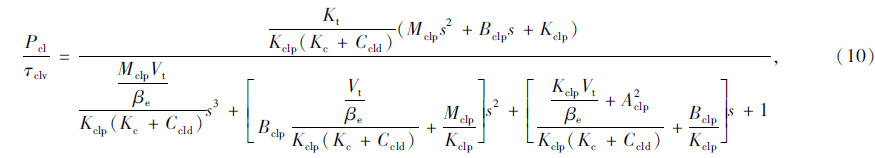
为比较模型对系统的真实性质反映情况,测试模型的预测精度,引用均方根误差(RMSE)来评价预测效果:

选用不同占空比变化率和油液温度的测试数据,分别对机理线性模型、SVM模型和RBF神经网络模型的均方根误差进行比较,得出结果如表 3所示。
| 试验组 | 训练集 | 测试集 | 均方根误差 | ||||||
| 样本数 | 油温/℃ | 占空比变化率 | 样本数 | 油温/℃ | 占空比变化率 | 机理线性模型 | RBF神经网络 | SVM | |
| 1 | 607 | 65 | 100/30 | 13 | 65 | 100/30 | 0.076 7 | 0.023 4 | 0.011 9 |
| 23 | 607607 | 6565 | 100/30100/30 | 1313 | 6539 | 100/10100/30 | 0.077 30.094 8 | 0.032 50.025 6 | 0.012 00.016 2 |
| 4 | 607 | 65 | 100/30 | 13 | 39 | 100/60 | 0.108 2 | 0.033 1 | 0.019 9 |
| 5 | 610 | 39 | 100/30 | 45 | 65 | 100/60 | 0.082 7 | 0.034 4 | 0.017 5 |
| 6 | 409 | 36 | 100/10 | 44 | 36 | 100/15 | 0.098 1 | 0.011 5 | 0.010 4 |
| 7 | 202 | 65 | 100/10 | 45 | 36 | 100/15 | 0.080 7 | 0.025 2 | 0.013 3 |
第1~4组的训练集相同,对比分析不同的占空比变化率和油温下离合器的接合压力。图 9为第1组的测试结果,测试集与训练集完全相同,离合器机理模型的接合压力与真实值相差较大,但SVM模型和RBF神经网络模型的接合压力均能较好地跟随真实值。

|
| 图 9 第1组测试结果 Fig. 9 Test result of 1st group |
第2组测试集的油温与训练集相同,为65 ℃,但占空比变化率不同于训练集,为100/10,测试结果如图 10所示,SVM模型和神经网络模型的接合压力也能较好地跟随真实值,但3种模型的均方根误差较第1组有一定程度的增大。

|
| 图 10 第2组测试结果 Fig. 10 Test result of 2nd group |
第3组测试集的占空比变化率与训练集相同,为100/30,但油温与训练集不同,为39 ℃。测试结果如图 11所示,SVM模型和RBF神经网络模型仍保持与真实值的跟随性,但3种模型的均方根误差持续增大。

|
| 图 11 第3组测试结果 Fig. 11 Test result of 3rd group |
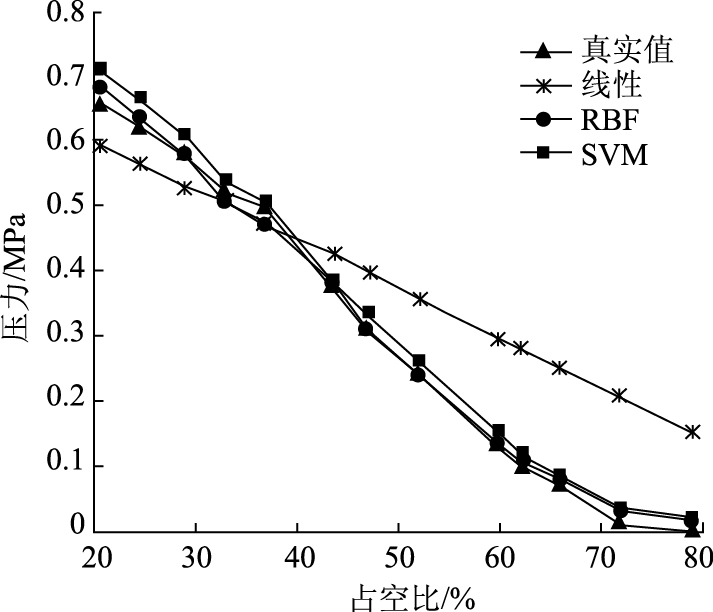
第4组测试集的油温和占空比变化率均不同于训练集,其中油温为39 ℃,占空比变化率为100/60,测试结果如图 12所示。当测试集占空比变化率和油温均不同于训练集时,SVM模型和RBF神经网络模型的误差均明显增大。
|
| 图 12 第4组测试结果 Fig. 12 Test result of 4th group |
前4组结果中,当占空比变化率或油温变化时,模型的均方根误差均会随之变化,因此可知占空比变化率和油温是影响离合器控制系统非线性的重要因素。第5~7组为随机选取的训练集与测试集,表 3中的测试结果显示SVM模型误差均小于RBF神经网络模型误差和机理线性模型误差,说明SVM模型有较强的泛化能力,且SVM模型能更好地反映液压执行机构的真实性质,对温度、占空比变化率有一定的补偿效果。
4 基于预测模型的整车起步仿真 4.1 整车起步仿真模型的建立整车起步仿真模型主要包括发动机动力学模型、离合器动力学模型、起步阻力矩模型、离合器液压模型和离合器主、从动片目标接合压力模型等。本文以离合器SVM预测模型代替其传统的机理模型,以某国产轿车为研究对象进行整车建模仿真,建立如图 13所示的整车起步仿真模型。

|
| 图 13 整车仿真模型 Fig. 13 Simulation model of vehicle |
该车型主要技术参数如表 4所示。
| 汽车满载质量/kg | 离合器从动盘至车轮部分的转动惯量/(kg·m2) | 车轮半径/m | 主减速箱传动比 | 变速箱传动比 | 传动系统机械效率 | 离合器内、外半径/m | 离合器摩擦片数目 | 离合器摩擦片摩擦系数 |
| 1 500 | 1.12 | 0.31 | 3.85~4.35 | 0.445~2.6 | 0.92 | 0.1/0.15 | 4 | 0.22 |
起步性能的好坏以起步平顺性和离合器工作寿命来衡量,本文以车辆起步的冲击度作为衡量汽车起步性能好坏的标准[12]。根据建立的整车仿真模型,分别改变油门开度a和油门开度变化率da/dt得到不同的起步意图,以测试基于传统机理模型和SVM模型的整车仿真效果。分别在小油门(a=10%,da/dt=30%)、大油门(a=75%,da/dt=45%)起步时进行仿真,得到如图 14~图 15所示的冲击度仿真结果。

|
| 图 14 小油门平地起步的冲击度(a=10%,da/dt=30%) Fig. 14 Impact degree of small throttle starting (a=10%,da/dt=30%) |

|
| 图 15 大油门平地起步的冲击度(a=75%,da/dt=45%) Fig. 15 Impact degree of large throttle starting(a=75%,da/dt=45%) |
由仿真结果可以看出,无论是小油门起步还是大油门起步,SVM模型控制的冲击度均小于其传统机理模型控制的冲击度。因此,基于SVM离合器智能预测模型的控制效果要优于传统的机理模型。
4.3 不同起步意图时的整车试验分析对于CVT液压系统的复杂性及执行机构的时变性和非线性,仅靠理论分析和建模仿真难以说明控制策略的效果。为验证本文所提出的基于预测模型的控制效果,在国产野马F10越野车上进行起步冲击度试验,分别在平地小油门(油门开度a=35%)和大油门(油门开度a=75%)起步时进行试验,结果分别如图 16~图 17所示。

|
| 图 16 小油门起步冲击度 Fig. 16 Impact degree with small throttle starting |

|
| 图 17 平地大油门起步冲击度 Fig. 17 Impact degree with large throttle starting |
试验结果表明,发动机运转平稳,在2 s左右时冲击度达到最大值6 m/s3;在1.5 s左右时冲击度达到最大值8.4 m/s3。试验所得冲击度均未超出推荐值10 m/s3,车辆能够平稳起步。因此,试验结果与仿真结果基本一致。
5 结论基于台架试验数据,建立了离合器SVM和RBF神经网络模型,并与传统机理模型进行了比较分析。结果表明,基于SVM和RBF神经网络模型的离合器执行机构精度均优于其传统的机理模型。基于离合器SVM模型,分别在小油门起步和大油门起步时完成了整车的仿真试验。结果表明,SVM模型更能准确地反映执行机构的真实性能,基于该模型的整车起步过程的冲击度较小,对提高车辆的舒适性和离合器起步控制品质有一定的参考价值。
| [1] | 张宝山,张伯英,周云山,等.金属带式无级变速器液压控制系统的仿真[J].农业机械学报,2002,33(2):20-24.ZHANG Bao-shan,ZHANG Bo-ying,ZHOU Yun-shan,et al.Simulation of a CVT Control System[J].Transactions of the Chinese Society of Agricultural Machinery,2002,33(2):20-24. |
| [2] | 夏晶晶,陈勇,胡辰.CVT湿式离合器液压控制系统设计[J].液压与气动,2010(10):45-47.XIA Jing-jing,CHEN Yong,HU Chen.Design of the Hydraulic Control System for CVT Clutch[J].Chinese Hydraulics & Pneumatics,2010(10):45-47. |
| [3] | 吴光强,杨伟斌,秦大同.双离合器式自动变速器控制系统的关键技术[J].机械工程学报,2007,43(2):13-21.WU Guang-qiang,YANG Wei-bin,QIN Da-tong.Key Technique of Dual Clutch Transmission Control System[J].Chinese Journal of Mechanical Engineering,2007,43(2):13-21. |
| [4] | MONTANARI M,RONCHI F,ROSSI C,et al.Control and Performance Evaluation of a Clutch Servo System with Hydraulic Actuation[J]. |
| [5] | HURON G.Numerical Simulations of SAE#2 Machine Tests[EB/OL].[2014-07-10].http://papers.sae.org/1999-01-3617. |
| [6] | 罗永革.湿式离合器金属带式无级变速器(CVT)控制策略研究[D].杭州:浙江大学,2001.LUO Yong-ge.A Study on Control Strategy of Metal Pushing V-belt CVT with Wet-clutch[D].Hangzhou:Zhejiang University,2001. |
| [7] | 刘振军,郝宏伟,董小洪,等.湿式双离合器自动变速器换挡控制与仿真分析[J].重庆大学学报:自然科学版,2011,34(1):7-13.LIU Zhen-jun,HAO Hong-wei,DONG Xiao-hong,et al.Shifting Control and Simulation of Wet Dual Clutch Transmission[J].Journal of Chongqing University:Natural Science Edition,2011,34(1):7-13. |
| [8] | 程秀生,冯魏,陆中华,等.湿式双离合器自动变速器的起步控制[J].江苏大学学报:自然科学版,2010,31(2):145-149.CHENG Xiu-sheng,FENG Wei,LU Zhong-hua,et al.Starting Control of Wet Double Clutch Transmission[J].Journal of Jiangsu University:Natural Science Edition,2010,31(2):145-149. |
| [9] | 袁小艳,刘爱伦.基于PSO算法的支持向量机核参数选择问题研究[J].控制理论与应用,2007,26(5):5-8.YUAN Xiao-yan,LIU Ai-lun.Kernel Parameter Selection of the Support Vector Machine based on Particle Swarm Optimization[J].Techniques of Automation and Applications,2007,26(5):5-8. |
| [10] | ZHAO C Y,ZHANG H X,ZHANG X Y,et al.Application of Support Vector Machine(SVM) for Prediction Toxic Activity of Different Data Sets[J].Toxicology,2006,217(2/3):105-119. |
| [11] | 彭显刚,胡松峰,吕大勇.基于RBF神经网络的短期负荷预测方法综述[J].电力系统保护与控制,2011,39(17):144-148.PENG Xian-gang,HU Song-feng,LV Da-yong.Review on Grid Short-term Load Forecasting Methods Based on RBF Neural Network[J].Power System Protection and Control,2011,39(17):144-148. |
| [12] | 吴光强,司建玉.双离合器自动变速器起步的智能控制策略[J].同济大学学报:自然科学版,2012,40(1):81-87.WU Guang-qiang,SI Jian-yu.Launching Intelligent Control Strategy for Dual Clutch Transmission[J].Journal of Tongji University:Natural Science Edition,2012,40(1):81-87. |
 2016, Vol. 31
2016, Vol. 31
