扩展功能
文章信息
- 胡兴华, 隆冰, 朱晓宁
- HU Xing-hua, LONG Bing, ZHU Xiao-ning
- 考虑绿时损失均衡的公交优先交叉口配时优化
- Timing Optimization for Bus Priority Signalized Intersection Considering Green Loss Equilibrium
- 公路交通科技, 2016, Vol. 31 (2): 96-104
- Journal of Highway and Transportation Research and Denelopment, 2016, Vol. 31 (2): 96-104
- 10.3969/j.issn.1002-0268.2016.02.015
-
文章历史
- 收稿日期: 2015-06-03
2. 重庆市交通规划研究院, 重庆 400000
2. Chongqing Transport Planning Institute, Chongqing 400000, China
公交信号优先是提高公交运行效率,增加公交吸引率的一种有效方法。Wu等 [1, 2]针对公共车辆按照不同的信号需求设置了3种不同运行特征的预处理信号,探讨了3种预处理信号配时与优先车辆和非优先车辆的延误分析方法。Wahlstedt等[3, 4]利用仿真的方法分析了公交信号优先对信号交叉口的影响。Liu等[5]利用解析法分别对优先和非优先进口道车辆在延长绿灯时间和绿灯起亮提前两种优先策略进行了延误分析。Jiang等[6]考虑了交叉口各进口道动态的交通流量到达过程,以定数理论为基础,利用Markov特性提出了自适应信号控制条件下的平均车辆延误计算模型[1]。Keita等[7]分别对排队增量累计IQA与道路通行能力手册HCM两种延误计算方法进行了对比分析。刘广萍等[8, 9]分别对交叉口进口道同时处于饱和与非饱和两种状态进行了延误分析与计算。Liu等[10]考虑了交叉口的最大通行能力,以周期内交叉口延误车辆数最少为目标函数建立了信号配时优化模型,并采用差分进化细菌觅食求解算法对其进行求解。王殿海等[11]考虑了公交优先控制策略对干线协调的影响,提出了以干线协调为上层,以公交优先为下层的双层优化方法,在不破坏协调相位绿波带的情况下采用绿灯延长或提前启亮的方式为公交提供信号优先。王正武等[12]在基于规则与优化的自适应公交优先控制中考虑了公交优先的系统效益和优先措施对社会车辆的负面影响,并构建了双层规划模型同时对相位相序和配时参数进行优化。柳祖鹏等[13]分别在绿灯和红灯相位下,针对当前相位保持绿灯和需要绿灯的需求程度提出了绿灯需求度的概念,并设计了绿灯和红灯相位下绿灯需求度的计算方法,提出了一种基于绿灯需求度的相位切换决策流程,在此基础上实现了基于绿灯需求度的公交信号优先控制。
上述关于公交优先交叉口配时优化的研究中,其研究对象主要集中对优先策略和优先策略时长的优化,考虑了随优先策略变化的信号周期,不利于多交叉口的协调控制。本文在不改变原有周期的前提下,对优先策略的负面影响进行整周期均衡,并对均衡参数进行优化。提出了延长绿灯时间、缩短红灯时间、插入优先相位3种策略的绿时损失均衡方法,在此基础上进行了延误分析计算,以交叉口减少人总延误最大为目标函数建立了配时优化模型,并设计了求解算法进行实例分析。
1 面向绿时损失均衡的公交优先感应控制策略公交优先策略会对非优先相位造成绿时损失,在考虑绿时损失均衡过程中,需要压缩非优先相位的绿时[14],但仅压缩非优先相位的绿时不利于提高绿时利用效率且与实际相位之间承接不相吻合,因而在压缩非优先相位绿时同时需要向相邻相位拓展绿时。设t为公交到达时刻,g为相位有效绿灯时间,ge为相位延长绿灯时间,gmin为相位最小绿灯时间;r为相位有效红灯时间,rs为缩短红灯时间;gp为插入相位时长,gp_min为最小插入相位时长。
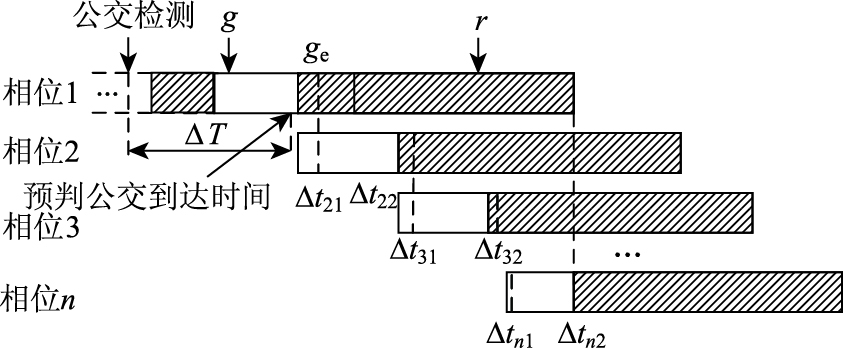
1.1 延长绿灯时间如图 1所示,检测公交车到达时,公交通行相位为绿灯,但剩余绿灯时间不足以让公交车通过交叉口,在最大延长范围ge_max内采用延长绿灯时间的优先策略,ge_max取决于相邻非优先相位的最小绿灯时间。为了减弱第1相位优先控制对相邻相位的冲击,需将其造成的绿时损失通过相位传递,逐级耗散在整个周期中。由此,从第2相位绿时末端向下一相位延长绿时以减少其绿时损失,而后,第3相位也依次向下延长绿灯时间,由此实现绿时损失在各相位逐渐衰减。
|
| 图 1 延长绿灯时间的绿时损失均衡方法 Fig. 1 Green loss equilibrium method for green extension |
对于第i相位,在相位绿时左端,因前一相位绿时延长而受到绿时损失Δti1;而在相位绿时右端,则会因相位绿时延长而得到绿时弥补Δti2,则有:
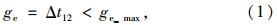
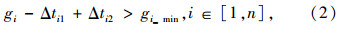
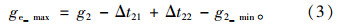
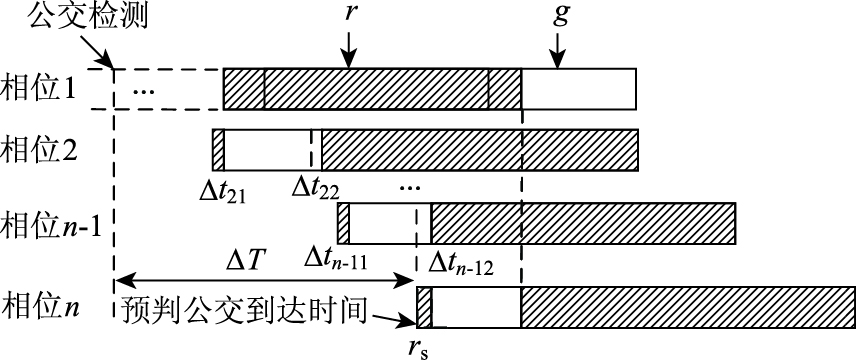
如图 2所示,检测公交车到达时,公交通行相位为红灯,且执行即将结束,同时上一相位的绿灯执行时间已超过最小绿灯时间,在最大缩短范围rs_max内采用缩短红灯的优先策略,rs_max取决于非优先相位的最小绿灯时间。为了均衡非优先相位的绿时损失,在第n-1相位绿时始端依次向前延长绿时以减小其绿时损失,由此实现绿时损失在整周期内的均衡。
|
| 图 2 缩短红灯时间绿时损失均衡方法 Fig. 2 Green loss equilibrium method for red truncation |
对于第i相位,在相位绿时右端,因后一相位缩短红时而受到绿时损失Δti2;而在相位绿时左端,则会因相位绿时延长而得到绿时弥补Δti1,则有:
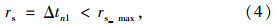
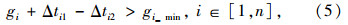
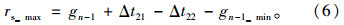
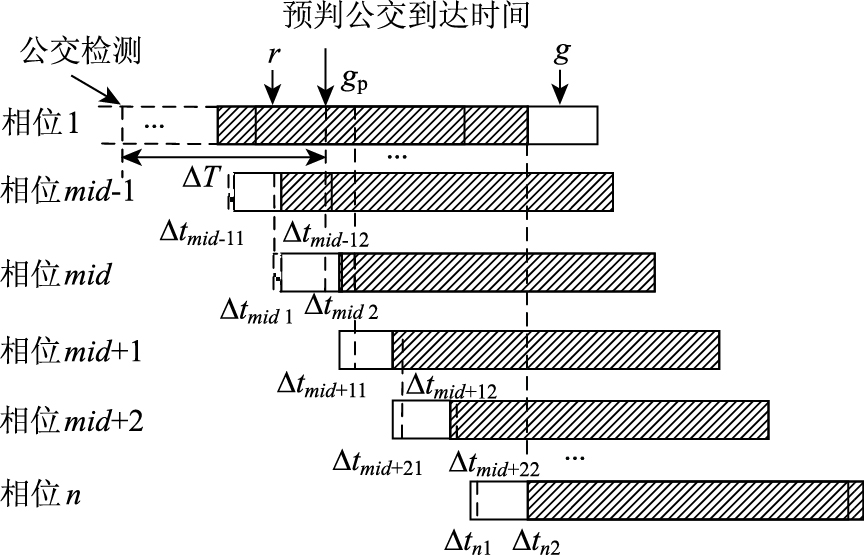
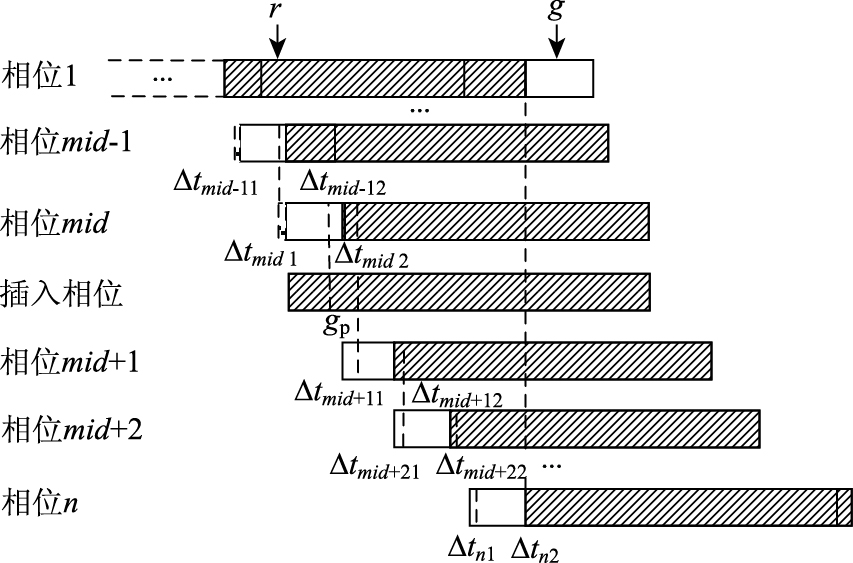
如图 3所示,检测公交车到达时,公交通行相位为红灯,而红灯执行时间只到中端,对应绿时相位已执行完最短绿灯时间且剩余绿时小于插入相位时长,在最大插入时长gp_max内采用插入相位的优先策略。为了避免绿时相位在插入相位后产生过短绿时残余,同时减少插入相位对单一非优先相位的冲击,选择当前绿时相位末端为插入时刻,将绿时损失分摊到两相邻相位,设phase mid,phase mid+1为直接承担插入相位损失的两相邻相位。为了降低非优先相位的绿时损失,分别在第mid相位绿时始端向前弥补绿时,而在mid+1相位绿时末端向后延长绿时,以此实现mid,mid+1相位的绿时损失在整周期内均衡。
|
| 图 3 插入优先相位绿时损失均衡方法 Fig. 3 Green loss equilibrium method for phase insertion |
对于第i相位,i∈[1,mid],在相位绿时右端,因后一相位绿时延长而受到绿时损失Δti2;而在相位绿时左端,则会因相位绿时延长而得到绿时弥补Δti1。对于第k相位,k∈[mid+1,n],在相位绿时左端,因前一相位延长绿时而受到绿时损失Δtk1;而在相位绿时右端,则会因相位绿时延长而得到绿时弥补Δtk2。
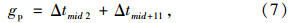
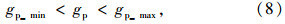
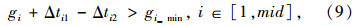
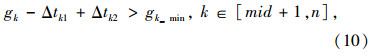
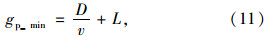
式(11)中,D为公交经过交叉口的轨迹线长度;v为公交在交叉口内的运输速度;L为插入相位绿灯损失时间。
如图 1~图 3所示的绿时损失均衡过程中,各相位通过相邻相位之间的承接关系,利用相位绿时左端和右端的时长变化,逐步减弱优先相位对非优先相位的不利影响。对于插入优先相位策略,绿时变化发生在相位中部,可将之视为一个绿灯时长为0的独立新增相位,如图 4所示,通过新增相位实现绿时两端的时长变化在周期内传递。
|
| 图 4 插入优先相位的绿时变化传递过程 Fig. 4 Green time changing process of preferred phase insertion |
由上分析可知,延长绿灯时间、缩短红灯时间、插入优先相位3种优先策略的绿时损失均衡过程均可描述为相位绿时两端的时长变化。
2 交叉口进口道车辆延误分析
|
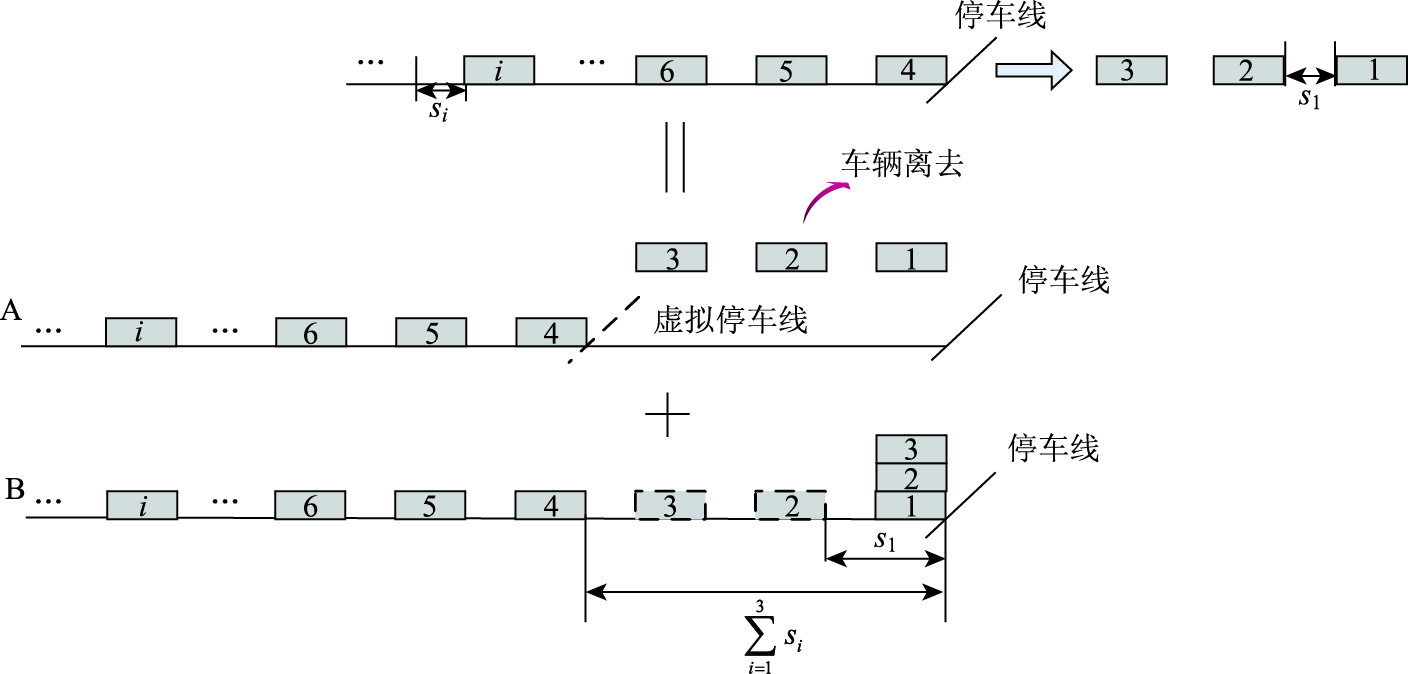
| 图 5 交叉口进口道车辆的到达离开过程 Fig. 5 Vehicles' arrival and departure processes at intersection entrance lane |
图 5为交叉口进口道上车辆的到达离开过程,图中将交叉口进口道上车辆的到达离开过程描述为A,B两个过程的叠加。过程A考虑了静态车流在信号控制下的排队和离去,而将进口道停车线想象为可移动的虚拟线,并将静态排队车流驶离停车线的过程描述为虚拟线向后移动的过程;过程B在A的基础上,考虑了车流向交叉口停车线的动态累积过程。图中,si为第i辆车的车头间距。
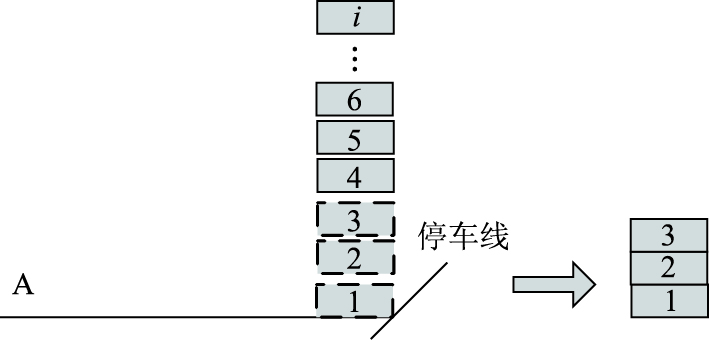
2.1 过程A的延误分析图 6为交叉口停车线后静态车流的排队—驶离过程,该过程不考虑车辆的体积和车头间距,而将车流虚拟为一串纵向的质点累积。
|
| 图 6 过程A中车辆的到达离开过程 Fig. 6 Vehicle arrival and departure process A |
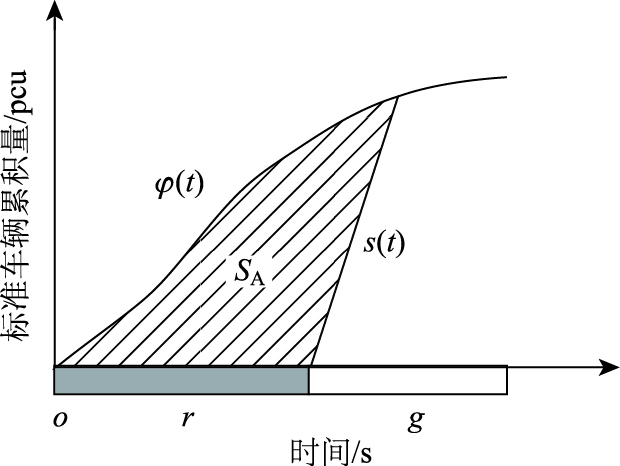
由图 6分析可知,交叉口进口道中过程A的延误分析可描述为如图 7所示的几何分析。图中,横轴t为时间,纵轴Q为标准车辆累积量,φ(t)为交叉口停车线车辆累积函数,s(t)为进口道车辆离去函数。阴影面积SA即为交叉口进口道中过程A的车辆延误DA。
|
| 图 7 过程A中车辆在周期内的延误分析 Fig. 7 Vehicle delay analysis of a period in process A |
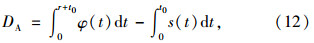
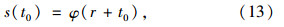
式中t0为延误计算过程中的中间变量。
2.2 过程B的延误分析由图 5中过程B的分析可知,车流的累积排队过程自身也会造成延误,车流排队长度越长,车流起动响应越慢。考虑车辆在排队列中均匀分布,可将过程B的延误描述为进口道车流排队中起动波的传播过程。其中,vs为进口道车流起动波传播速度,s为平均车头间距,v为路段车辆平均运行速度,as1为车辆启动加速度,as2为车辆制动加速度。
由此,交叉口进口道中排队车辆数n(t):
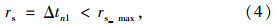
对交叉口t时刻到达车辆,其进口道过程B的延误可描述为:
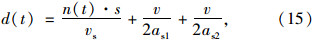
则交叉口进口道过程B的延误为:
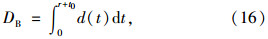
综上,交叉口进口道中的车辆延误D可描述为过程A与B的叠加,则有:

(1)左端绿时延长
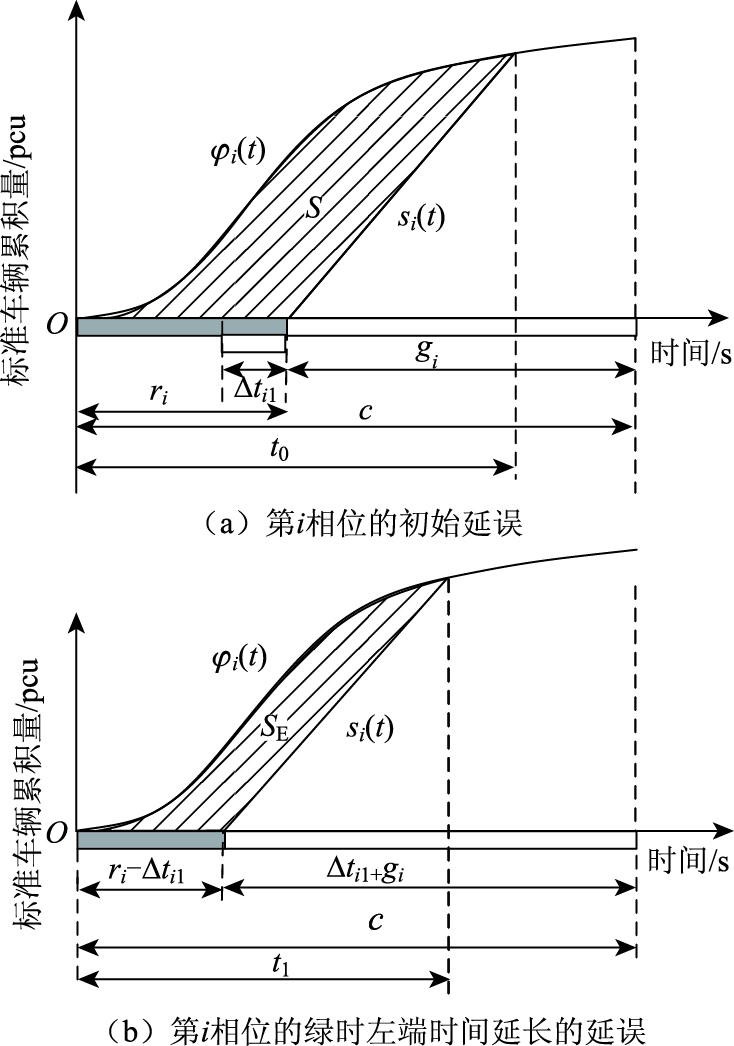
图 8为第i相位左端绿灯时间延长下的过程A延误分析。φi(t)为交叉口第i相位进口道车辆到达累积函数;Si(t)为交叉口第i相位进口道车辆离开累积函数。由图可知,阴影面积S即为第i相位的初始延误;阴影面积SE为绿时左端时间延长的延误;面积差S-SE即为第i相位左端绿时变化引起的延误减少量Δdi1_AO。
|
| 图 8 第i相位绿时左端延长时间引起的延误减少量分析 Fig. 8 Analysis of delay decrement caused by green extension at left end of phase i |
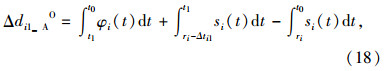
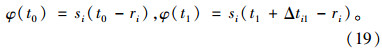
第i相位左端绿灯时间延长下的过程B延误减少量Δdi1_BO为:
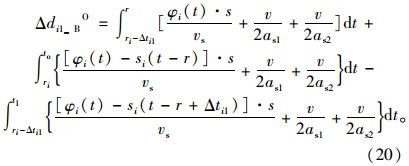
第i相位左端绿灯时间延长的延误减少量Δdi1O为:
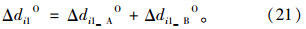
(2)左端绿时缩短
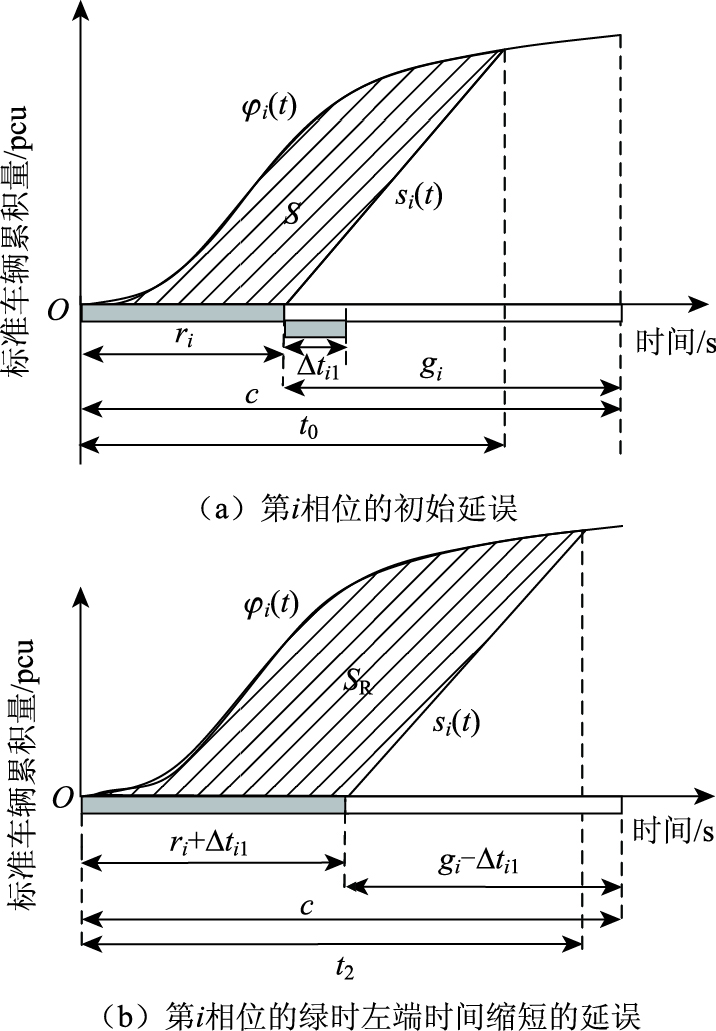
图 9为第i相位左端绿灯时间缩短下的过程A延误分析。由图可知,阴影面积S即为第i相位的初始延误;阴影面积SR为绿时左端时间缩短的延误;面积差SR-S即为第i相位左端绿时变化引起的延误增加量Δdi1_AL。
|
| 图 9 第i相位绿时左端缩短时间引起的延误增加量分析 Fig. 9 Analysis of delay increment caused by green truncation at left end of phase i |
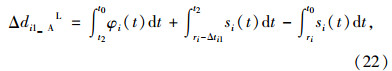
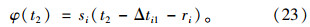
第i相位左端绿灯时间缩短下的过程B延误增加量Δdi1_BL为:
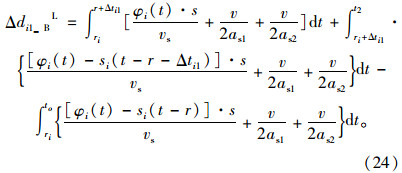
第i相位左端绿灯时间缩短的延误增加量Δdi1L为:
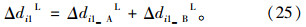
(1)右端绿时延长
图 10为第i相位右端绿灯时间延长下的过程A延误分析。由图可知,阴影面积S即为第i相位的初始延误;阴影面积SE为绿时右端时间延长的延误;面积差S-SE即为第i相位右端绿时变化引起的延误减少量Δdi2_AO。
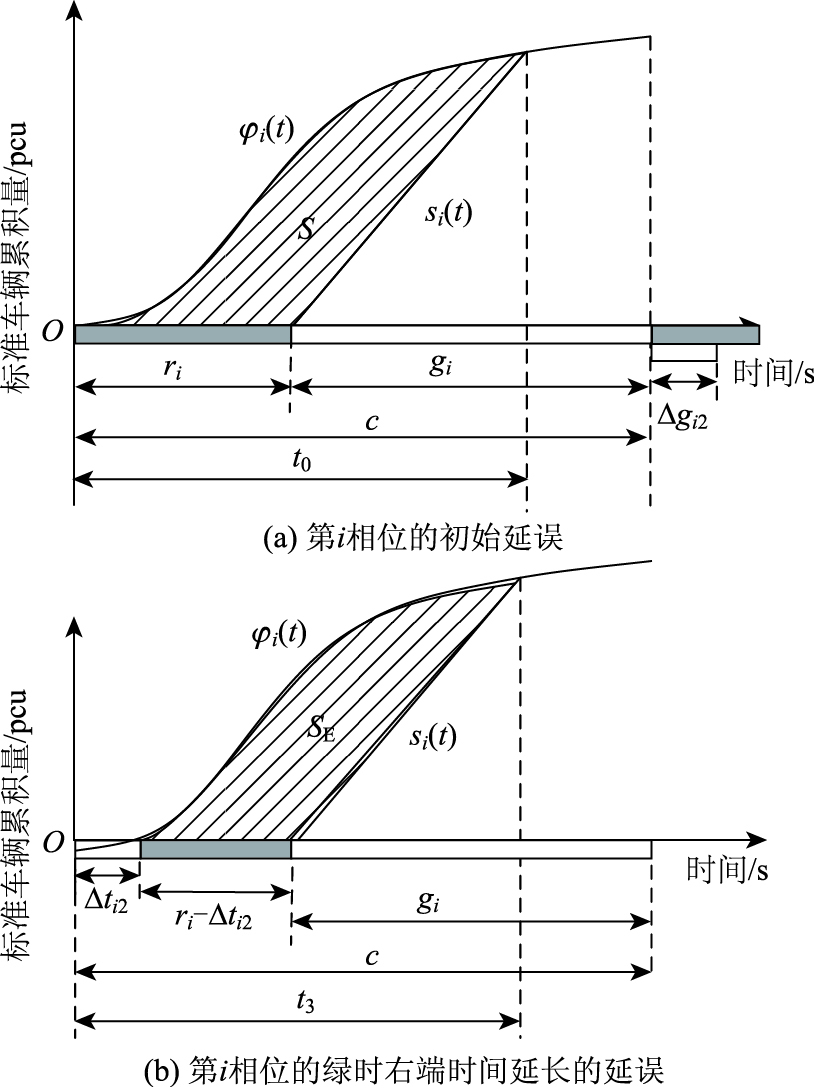
|
| 图 10 第i相位绿时右端延长时间引起的延误减少量分析 Fig. 10 Analysis of delay decrement caused by green extension at right end of phase i |
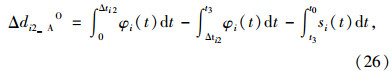
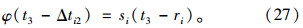
第i相位右端绿灯时间延长下的过程B延误减少量Δdi2_BO为:
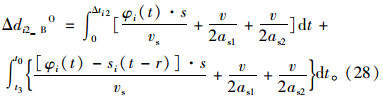
第i相位右端绿灯时间延长的延误减少量Δdi2O为:
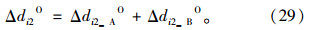
(2)右端绿时缩短
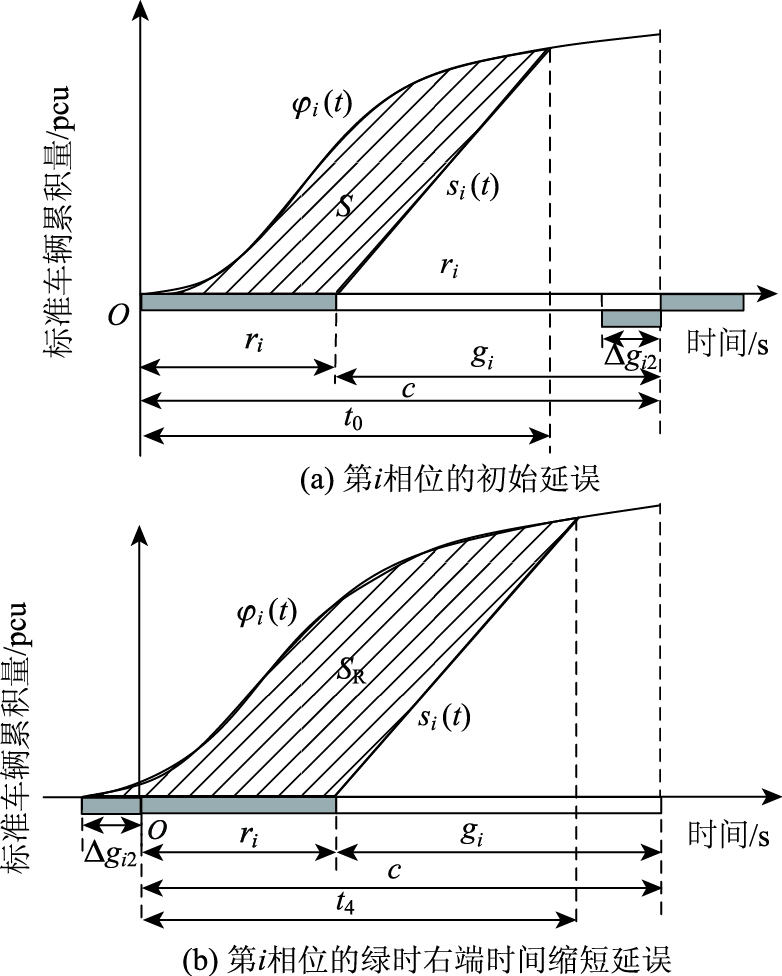
图 11为第i相位右端绿灯时间缩短下的过程A延误分析。由图可知,阴影面积S即为第i相位的初始延误;阴影面积SR为绿时右端时间缩短的延误;面积差SR-S即为第i相位右端绿时变化引起的延误增加量Δdi2_AL。
|
| 图 11 第i相位绿时右端缩短时间引起的延误增加量分析 Fig. 11 Analysis of delay increment caused by green truncation at right end of phase i |
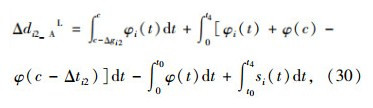
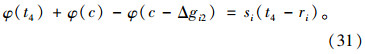
第i相位右端绿灯时间缩短下的过程B延误增加量Δdi2_BL为:
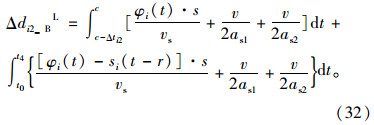
第i相位右端绿灯时间延长的延误增加量Δdi2L为:
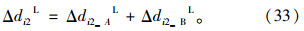
交叉口第i相位延误变化量ΔDi为:
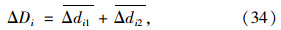
式中,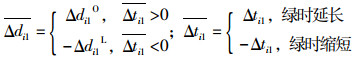
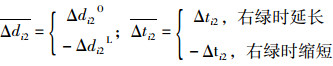
(1)基于绿时损失均衡的公交优先配时优化模型
以周期时长内车辆总延误最小为目标来确定交叉口的配时参数对于公交车辆所占比例较大的相位是不公平的,公交车单车载客量明显大于社会车辆,而减少交叉口延误的根本目的是减少人的延误,提高人的出行效率[14]。因而需要对交叉口内人的延误进行分析,以交叉口减少的人的延误最大作为优化的目标。对于优先相位,绿时延长受益的不仅有公交车辆,还包含部分社会车辆;而对于受到绿时损失的非优先相位,其社会车辆和公交车辆也均会增加延误。假设cari(t)为第i相位社会车辆到达累积函数; busi(t)为第i相位公交车辆到达累积函数;pbus为一个pcu的公交车平均载客数(即公交车的平均载客数除以其当量小汽车换算系数);pcar为一个pcu的社会车辆平均载客数,参照交叉口车辆延误分析,得到各相位乘客延误为:
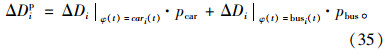
采用公交优先策略后,以周期内交叉口减少人的总延误最大为目标函数、保障非优先相位的最小绿时为约束条件进行配时优化,得到如下绿时损失耗散的配时优化模型。
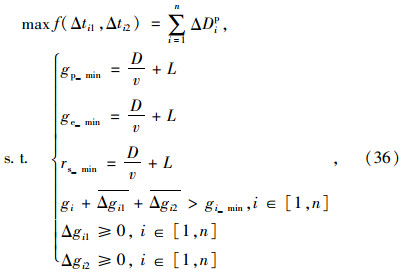
式中,f(Δti1,Δti2)为以Δti1,Δti2为变量的目标函数,按上模型优化后得到各相位的绿灯时长gi为:gi=gi+Δti1+Δti2,i∈[1,n]。
(2)算法设计
上述优化模型(36)为非线性目标函数,线性约束的规划问题,因而可以借用Frank-Wolfe算法[15]的基本思想设计求解算法,利用对角化技术分别对目标函数中的未知变量Δt2,Δt3,…,Δtn进行优化求解。将目标函数改写为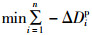 ,具体步骤如下:
,具体步骤如下:
①初始化:Δti0=0,i∈[2,mid-1]∪[mid+2,n],Δtmid0=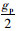 ,Δtmid+10=gp-Δtmid。
,Δtmid+10=gp-Δtmid。
②对角化:示目标函数为f(Δt2,Δt3,…,Δti,…,Δtn),初始化i=2,count=0。
Step1:设置收敛准则,ΔT=(Δt2,Δt3,…,Δtn),‖ΔTcount-ΔTcount-1‖<gap,若ΔTcount满足收敛准则,停止迭代,返回ΔTcount;
Step2:检查i,如果i>n,则令i=2,count=count+1,返回step1;
Step3:一阶Taylor逼近,暂时固定Δt2,Δt3,…,Δti-1,Δti+1,…,Δtn,对f关于Δti一元展开:f(Δt2,Δt3,…,Δti,…,Δtn)=f(ΔTk)+▽f·(Δtik)T(Δti-Δtik);
Step4: 求解线性规划问题:minf(ΔTk)+▽f(Δtik)T(Δti-Δtik)
s.t Δti∈S,得到优化解Δtiky,Yk=(Δt2k,Δt3k,…,Δtiky,…,Δtnk);
Step5:收敛判断,如果▽f(Δtik)T(Δtiky-Δtik)=0或者Δtik+1-Δtik<gap,i=i+1,转到step2;
Step6:一维搜索,求解线性规划问题:minf[ΔTk+λ(Yk-ΔTk)]
s.t 0≤λ≤1,求解最优步长λk,得到:ΔTk+1=ΔTk+λk(Yk-ΔTk),转到Step4。
下面以一四相位的交叉口为例,假设交叉口进口道车流为线性到达,以交叉口进口道饱和流率作为车流离去函数。交叉口相位组成与车辆到达离去情况如表 1所示,假设一个pcu公交车辆平均载客率为30人,一个pcu社会车辆平均载客率为3人,车辆启动波传递速度为4 m/s,进口道排队车列的平均车头间距为6 m。
| 相位 | 第1相位 | 第2相位 | 第3相位 | 第4相位 | ||||
| 相位流向 | S-N | N-S | S-W | N-E | E-W | W-E | E-S | W-N |
| 相位有效绿灯时间/s | 50 | 40 | 30 | 30 | ||||
| 社会车辆到达率/ (pcu·h-1) | 0.45 | 0.45 | 0.19 | 0.19 | 0.13 | 0.13 | 0.12 | 0.12 |
|
公交车辆到达率/ (pcu·s-1) | 0.06 | 0.06 | 0.02 | 0.02 | 0.01 | 0.01 | 0.01 | 0.01 |
| 相位最短绿灯时间/s | 40 | 25 | 20 | 20 | ||||
假设在第1相位红时运行中端检测到公交优先请求,在第1相位插入优先相位,根据交叉口规模,取插入相位最短时长为gp_min=8 s。
将数据代入优化模型(36),按照上述算法对其进行求解。在求解Δti1,Δti2过程中,目标函数中有Δt22+Δt31=gp。通过计算得到各相位的绿时均衡参数如表 2所示。
| 相位 | Δti1 | Δti2 | gi | ri | Δdi |
| 第1相位 | 0 | 1.4 | 63.2 | 86.8 | -1 654 |
| 第2相位 | 1.4 | 4.2 | 37.2 | 112.8 | 86.8 |
| 插入相位(公交) | 4.2 | 10.3 | 14.6 | 135.0 | -27 |
| 第3相位 | 10.3 | 3.1 | 22.8 | 127.2 | 91.4 |
| 第4相位 | 3.1 | 0 | 26.9 | 123.1 | 60.3 |
(1)从各相位绿时均衡参数计算结果来看,插入公交优先相位对交叉口的冲击得到了逐级耗散,各非优先相位的绿时损失均在可接受的范围内。其中,第2,3,4相位绿时损失时间分别为2.8,7.2,3.1 s,有效避免了非优先相位因绿时损失过度而无法排空。
(2)通过各相位绿时左端和右端的时长变化传递,将交叉口富余绿时资源协调到效益最高的相位,提高了交叉口绿时利用效率。从计算结果可以看出,将车流量较低的3,4相位富余绿时资源传递到车流量较大的第1相位,明显提升了交叉口通行效益。
(3)在周期内协调各相位的绿时资源,降低了优先策略对交叉口的扰动,同时,不改变下一周期的相位状态,避免了优先控制对交叉口群协调的破坏。
6 结论本文围绕因公交优先控制造成的绿时损失均衡问题,建立了考虑绿时损失均衡的公交优先配时优化模型,形成的基本结论如下:
(1)通过分析延长绿灯时间,缩短红灯时间,插入优先相位3种公交优先控制策略,提出了公交优先导致的绿时损失均衡方法,在绿时损失均衡过程中考虑相位之间的顺承关系,将公交优先的负面影响通过相邻相位传递至整周期,可避免非优先相位承受过大的绿时冲击。
(2)分别考虑相位两端的绿时损失和绿时弥补变化,提出了交叉口在损失均衡下的延误计算公式,可更准确地描述相位的延误变化。
(3)以减少交叉口人总延误最大为目标函数,非优先相位正常通行为约束条件建立了优化模型,算例计算结果表明,优化模型可有效地均衡绿时损失,非优先相位以较小的延误增加实现了公交优先。
可见,本文提出的绿时损失均衡方法不对信号周期造成扰动,基于绿时损失均衡的公交优先配时优化模型协调了周期内的绿时资源分配,提升了交叉口绿时资源利用效率和交叉口通行效益,在群交叉口的信号优先和多路公交优先请求的研究中也具有利用和发展的空间。
| [1] | WU J,HOUNSELL N.Bus Priority Using Pre-signals[J]. |
| [2] | 张卫华,陆化普.公交优先的预信号控制交叉口车辆延误分析[J].中国公路学报,2005,18(4):78-82.ZHANG Wei-hua,LU Hua-pu.Analysis of Vehicle Delay of Intersections with Pre-signals Based on Bus Priority[J].China Journal of Highway and Transport,2005,18(4):78-82. |
| [3] | WAHLSTEDT J.Impacts of Bus Priority in Coordinated Traffic Signals[J].Procedia-Social and Behavioral Sciences,2011,16(1):578-587. |
| [4] | 马万经,杨晓光.单点公交优先感应控制策略效益分析与仿真验证[J].系统仿真学报,2008,20(12):3309-3313.MA Wan-jing,YANG Xiao-guang.Efficiency Analysis of Transit Signal Priority Strategies on Isolated Intersection[J].Journal of System Simulation,2008,20(12):3309-3313. |
| [5] | LIU H J,ZHANG J,CHENG D X.Analytical Approach to Evaluating Transit Signal Priority[J]. |
| [6] | JIANG X C,PEI Y L.Delay Model of Adaptive Signal Control Using Fixed Number Theory[J]. |
| [7] | KEITA Y M,SAITO M.Evaluation of the IQA Delay Estimation Method[J].Procedia-Social and Behavioral Sciences,2011,16(16):792-802. |
| [8] | 刘广萍,裴玉龙.信号控制下交叉口延误计算方法研究[J].中国公路学报,2005,18(1):104-108.LIU Guang-ping,PEI Yu-long.Study of Calculation Method of Intersection Delay under Signal Control[J].China Journal of Highway and Transport,2005,18(1):104-108. |
| [9] | DION F,RAKHA H,KANG Y S.Comparison of Delay Estimates at Under-saturated and Over-saturated Pre-timed Signalized Intersections[J]. |
| [10] | LIU Q,XU J M.Traffic Signal Timing Optimization for Isolated Intersections Based on Differential Evolution Bacteria Foraging Algorithm[J].Procedia-Social and Behavioral Sciences,2012,43(4):210-215. |
| [11] | 王殿海,朱慧,别一鸣,等.干线公交优先信号协调控制方法[J].东南大学学报:自然科学版,2011,41(4):859-865.WANG Dian-hai,ZHU Hui,BIE Yi-ming,et al.Bus Signal Priority Method at Arterial Signal Progression[J].Journal of Southeast University:Natural Science Edition,2011,41(4):859-865. |
| [12] | 王正武,夏利民,罗大庸.单交叉口自适应公交优先控制[J].中国公路学报,2010,23(4):84-90.WANG Zheng-wu,XIA Li-min,LUO Da-yong.Adaptive Transit Priority Control at Isolated Intersection[J].China Journal of Highway and Transport,2010,23(4):84-90. |
| [13] | 柳祖鹏,李克平,倪颖.基于绿灯需求度的单点公交信号优先控制策略[J].同济大学学报:自然科学版,2013,41(3):408-414.LIU Zu-peng,LI Ke-ping,NI Ying.Isolated Transit Signal Priority Control Strategy Based on Demand Degree of Green[J].Journal of Tongji University:Natural Science Edition,2013,41(3):408-414. |
| [14] | 张卫华,石琴,刘强.公交优先信号交叉口延误计算与配时优化方法[J].华中科技大学学报:城市科学版,2004,21(4):30-33.ZHANG Wei-hua,SHI Qin,LIU Qiang.Study of Vehicle Delay Calculation and Optimal Signal-planning Method for Intersections with Induced Signal Based on Bus Priority[J].Journal of Huazhong University of Science and Technology:Urban Science Edition,2004,21(4):30-33. |
| [15] | FRANK M,WOLFE P.An Algorithm for Quadratic Programming[J].Naval Research Logistics Quarterly,1956,3(1):95-110. |
 2016, Vol. 31
2016, Vol. 31
