扩展功能
文章信息
- 王草, 邹阿鸣, 张龙, 李全旺
- WANG Cao, ZOU A-ming, ZHANG Long, LI Quan-wang
- 考虑车载历史信息的既有桥梁可靠度更新方法
- A Method for Updating Reliability of Existing Bridges Considering Historical Vehicular Loading Information
- 公路交通科技, 2016, Vol. 31 (2): 67-72
- Journal of Highway and Transportation Research and Denelopment, 2016, Vol. 31 (2): 67-72
- 10.3969/j.issn.1002-0268.2016.02.011
-
文章历史
- 收稿日期: 2015-03-30
对于既有桥梁,自然老化、车辆载荷增加以及使用过程中的碰撞损伤等因素会导致结构承载力的降低,从而影响其正常运营[1]。通常出于经济性的考虑,对所有危桥采取构件更换、加固等措施是不现实的;可取的做法是先对桥梁进行安全评价,以此作为后续制订维护、修复、管理措施的依据[2]。以概率统计为基础的结构可靠度分析,着眼于结构在服役过程中的承载力及荷载的不确定性,并基于实测和统计,为结构的安全性提供定量的评估。这一理论已成为既有桥梁状态评估和工程决策的基础[3]。
在对桥梁进行安全评估时,可以通过检测、试验等手段获得关于该桥梁的有效信息。利用这些信息,结合相应的计算技巧,可以有效提高评估结果的准确性。Law和Li[4]、Zhu和Wu[5]、Okasha等[6]的研究中利用了桥梁的健康监测数据来更新桥梁可靠度计算中的相关参数,进而更新可靠度的评估结果。但是这些方法中涉及到复杂的数学运算,且需要考虑到桥梁体系可靠度的整体效应,目前难以在实践中推广应用。桥梁荷载试验[7, 8]是一种常见的桥梁承载力评估方法,它能够直接确定桥梁的承载能力是否满足既定要求。然而,由于该方法成本昂贵,应用往往受到限制。Hall于1988年[9]提出将桥梁在服役过程中的车载历史看作该桥的试验荷载,并基于贝叶斯更新模型,给出了考虑历史车载信息的桥梁承载力更新方法。虽然该方法忽略了结构承载力的劣化,但为随后利用既有桥梁历史信息更新其承载力的研究和工程实践奠定了基础。此后,Stewart等[1]基于Monte Carlo模拟,研究了考虑结构劣化时,车载历史信息以及荷载试验对桥梁可靠度的更新效果。然而该方法需要多次重复模拟,计算代价巨大。因此,有必要寻求一种简便的方法来利用桥梁历史荷载信息对其可靠度进行更新。
本文基于贝叶斯更新理论,提出考虑历史车载信息的既有桥梁可靠度分析方法。该方法考虑了结构承载力的衰减和荷载过程的不确定性,并利用已有车载信息来更新桥梁的可靠度。本文方法给出了可靠度更新方法的显式公式,方便在实践中推广应用。
1 结构可靠度桥梁结构在时间段(0,T]内的可靠度,L(0,T),是指结构承受的荷载在时间(0,T]内不超过其承载能力的概率[10]。假设在t1,t2,… ,tn时刻分别发生了一次车载事件,对应的荷载效应分别记作S1,S2,…,Sn,则有:

式中,Pr{}表示括号中事件的发生概率;R1,R2,…,Rn分别表示t1,t2,…,tn时刻结构的承载力。
对劣化结构进行可靠度分析时,需要考虑到承载力的时变特征。通常可以用式(2)来描述结构承载力的衰减:

式中,R(t)为t时刻结构的承载力;R0为初始承载力;g(t)为衰减函数。g(t)可由实测数据拟合或者机理研究等手段获得。Enright等[11]研究了RC结构由于钢筋锈蚀引起的结构承载力劣化,给出了如式(3)所示的衰减函数:

式中,k1和k2为与时间t无关的参数;Tinitial表示劣化起始时间。这些参数的取值为:

对应于这3种退化类型,图 1给出了40 a内衰减函数g(t)随时间t的变化规律。在40 a的时间里,慢速、中速、退化对应的承载力分别下降1.5%,17.5%和30.5%。在后文的算例分析中,将会利用这3种衰减模型来描述混凝土结构承载力的衰减。

|
| 图 1 衰减函数随时间的变化 Fig. 1 Relationship between attenuation function and time |
一般情况下,结构承受的荷载过程具有随机性。为了考虑荷载过程的随机性,用平稳Poisson过程来描述荷载的发生,Poisson强度为λ(即在单位时间里平均有λ次荷载发生)。假定各荷载效应独立同分布,累积密度函数记作FS(s),如图 2所示,则式(1)变为[10]:

式中fR0(r)为初始承载力R0的概率密度函数;N=g(t)。

|
| 图 2 承载力衰减和荷载过程的随机性 Fig. 2 Stochastic loading process and resistance deteriorating process |
现考虑该结构从建成后T1时刻开始,后续T时间内的可靠度为L(T1,T1+T)。
首先,将式(5)改写为:

这表明,若λ,fR0(r)和FS(s)保持恒定,则结构在时间段(0,T]内的可靠度只取决于结构在此时间段内的承载力大小以及此时间段的始末时刻。因此,根据式(6):

注意到式(7)给出的结构可靠度考虑了结构承载力的衰减,但没有涉及在T1时刻之前的历史荷载信息。在下一节中将讨论如何利用车载历史信息对结构可靠度进行更新。
2 考虑车载历史的可靠度更新方法贝叶斯更新方法是处理后验概率问题的重要手段[12]。对于事件A和事件B,由贝叶斯公式,有
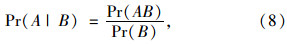
式中,A|B表示已知事件B发生时事件A发生;AB表示事件A和B同时发生。
现在考虑利用结构的服役历史信息来更新结构的可靠度。假设某结构已正常服役时间为T1,考虑其在随后的T时间内正常服役的可靠度,Lu(T1,T+T1)。
令事件A表示结构在时间段(T1,T+T1]内正常服役,事件B表示结构在时间段(0,T1]内正常服役,则:

注意到式(9)给出的是利用历史荷载信息更新后的结构可靠度,区别于式(7)给出的不考虑历史荷载信息的可靠度。
将式(8)代入式(9)中,有:

式中,Pr(B)=L(0,T1),在式(5)中已经给出;Pr(AB)=L(0,T+T1),且:

式中,N=g(t)将式(11)和式(5)代入式(10)中,

式(12)即为本文提出的考虑历史荷载信息的既有桥梁可靠度更新公式。公式中包含两重积分,可利用简单的黎曼积分进行计算。需要指出的是,一些积分技巧(比如Simpson积分法等[13])可以大大提高积分的计算效率。根据计算得到的Lu(T1,T+T1),可进一步给出对应的可靠度指标βu(T1,T+T1):

式中,ф-1()表示标准正态分布的累积密度函数反函数。类似地,对于式(7)中的L(T1,T+T1),对应的可靠度指标为:

本节通过算例说明式(12)的准确性,并通过对比式(7)和式(12),讨论结构可靠度的更新效果对车载强度、承载力衰减程度等因素的敏感性。

|
| 图 3 某预应力混凝土桥(单位:cm) Fig. 3 A prestressed concrete bridge(unit:cm) |
某预应力混凝土空心板桥已服役20 a,如图 3所示。混凝土强度为C40;预应力筋采用фs12.7钢绞线,7根为一束,每块板各7束。普通钢筋为HRB 335,每块板配置5ф12[14]。根据规范[15],计算得空心板跨中截面抗弯承载力为567.86 kN·m,结构自重引起的跨中弯矩为222.66 kN·m。考虑到初始承载力的不确定性,参考相关研究[10, 16],认为其服从对数正态分布,变异系数为0.15,则可得到初始抗弯承载力的概率密度函数fR0(r):

假定该桥梁承载力的衰减可以用式(3)和式(4)来描述(中速衰减)。根据规范[17],计算得该桥梁承受的一年一遇(λ=1)最大车载引起的空心板跨中截面弯矩服从极值I型分布,均值为 51.75 kN·m,标准差为18.59 kN·m,则其累积密度函数为FS(s)为:

式中s的单位为kN·m。
考虑到该桥梁处在重车密集的公路上,在服役过程中承受的实际车载远大于规范荷载[18],本文另外假设了两种车载效应,其引起的空心板跨中截面弯矩效应如表 1所示。
| 车载名称 | 分布类型 | 均值/(kN·m) | 变异系数 |
| 规范荷载 | 极值I型 | 51.75 | 0.36 |
| 车载1 | 极值I型 | 80.00 | 0.36 |
| 车载2 | 极值I型 | 100.00 | 0.36 |
| 注:变异系数为标准差与均值的比值。 | |||
考虑从当前时刻(T1=20 a)开始后若干年内该桥梁的可靠度,年最大车载效应假设为车载1。令式(12)中的T=1,2,… ,15 a,可分别计算得该桥从当前时刻开始,后续1,2,… 15 a内的可靠度Lu(T1,T+T1),进而由式(13)计算得各种情况对应的可靠度指标,如图 4所示。为了说明历史荷载对桥梁可靠度的更新效果,由式(7)计算出不考虑历史荷载情况下的可靠度L(T1,T+T1),将对应的可靠度指标绘制于图 4中。从中可以看到,考虑历史荷载信息可以显著提高桥梁可靠度的评估结果。

|
| 图 4 后续时间T内的桥梁可靠度指标 Fig. 4 Bridge reliability indices for subsequent T years |
为了说明式(12)的准确性,利用Monte Carlo模拟的方法重新计算考虑历史车载作用时,该桥梁在后续T年内的可靠度。具体步骤为:
(1)令变量COUNT1=0,COUNT2=0。
(2)随机生成初始抗弯承载力R0的一个样本值r0,服从式(15)所示的对数正态分布。
(3)随机生成一个Poisson数m,均值为λ×(T+T1);然后生成m个在(0,T+T1]上均匀且独立同分布的时刻t1<t2<…<tn<T1<tn+1<tn+2<…<tm<T+T1。
(4)对应于ti时刻,i = 1,2,…,m,根据车载效应累积密度函数,分别生成一个车载效应样本值si,其累积密度函数如式(16)所示。
(5)如果对于所有的i=1,2,…,n,均有r0×g(ti)-D≥si(D表示恒荷载),则说明桥梁在(0,T1]时间段内安全,令变量COUNT1增加1,然后进行下一步;否则,返回步骤(2)。
(6)如果对于所有的i=n+1,n+2,…,m,均有r0×g(ti)-D≥si,则说明桥梁在时间段(T1,T+T1]内安全,令变量COUNT2增加1。
(7)重复步骤(2)~(6)多次,则COUNT2/COUNT1的比值趋近于Lu(T1,T+T1)。
对于每个T值,分别通过100万次的蒙特卡洛数值模拟,得到Lu(T1,T+T1)模拟解对应的可靠度指标如图 4所示。从图中可见,Monte Carlo模拟的结果与式(12)的计算结果完全重合,由此证明了本文公式的正确性。
为了讨论车载效应大小对桥梁可靠度更新的影响,分别考虑规范荷载,车载1和车载2这3种情况,利用式(12)计算出桥梁更新后的可靠度,并与利用式(7)计算出的可靠度进行对比,对比结果如图 5所示。从图中可以看到,车载效应越大,则桥梁的可靠度越小,但可靠度的更新效果也越明显。以βu(20,35)为例,车载1对应的可靠度指标由更新前的1.86升至1.93,而车载2对应的可靠度指标由1.23更新至1.44。这说明超载车辆在引起桥梁更大服役风险的同时,也对桥梁可靠度的评估有着明显的提升作用,更新后的结构可靠度更能反映既有桥梁真实的可靠度水平,而不考虑车载历史则会低估桥梁的可靠度水平。另外可以看到,如果历史荷载是规范荷载,可靠度的更新效果不明显。这说明,在对桥梁进行可靠度评估时,如果实际车载不高于规范荷载,则考虑或不考虑历史信息得到的可靠度结果接近。

|
| 图 5 考虑不同车载作用时的可靠度指标 Fig. 5 Reliability indicies considering different vehicle loads |

|
| 图 6 考虑不同衰减程度时的可靠度指标 Fig. 6 Reliability indicies considering different deteriorating degrees |
考虑桥梁承载力的衰减程度对后续服役期内可靠度的影响。分别考虑如式(3)和式(4)所示的3种衰减速度,年最大车载效应为车载1。分别由式(12)和式(7)计算得到考虑/不考虑车载历史的结构态可靠度,对应可靠度指标如图 6所示。从图中可以看到,桥梁承载力衰减越快,结构的可靠度水平越低,但历史荷载信息对可靠度的更新效果越好。这表明,在对既有桥梁进行安全评估时,利用车载历史更新后的可靠度更能反映桥梁的真实可靠度水平,特别是在桥梁承载力退化严重的情况下;而在退化不严重的情况下,考虑/不考虑历史荷载信息得到的可靠度评估结果比较接近。
4 结论本文提出了考虑车载历史的既有桥梁可靠度更新方法,并结合算例,讨论了承载力衰减、车载大小对可靠度更新效果的影响,得到如下结论:
(1)本文给出了考虑车载历史的既有桥梁可靠度更新的显式公式,并结合算例表明了该公式的准确性。
(2)车载大小影响既有桥梁在后续服役期内的可靠度水平。车载越大,可靠度越小,但对可靠度的更新效果越明显。而在规范荷载水平下,利用车载历史更新后的可靠度与不考虑车载历史的可靠度结果基本一致。
(3)桥梁承载力衰减程度对既有桥梁可靠度有显著影响。承载力衰减越严重,可靠度越小,但历史荷载信息对可靠度的更新效果越明显。在桥梁承载力缓慢退化情况下(每年减少0.05%),考虑/不考虑历史荷载信息得到的可靠度比较接近。
(4)利用车载历史信息更新后的可靠度更能反映既有桥梁真实的可靠度水平。在实际车流存在超载现象,或者桥梁承载力劣化明显的情况下,应当对桥梁进行可靠度更新,以获得更为真实的评估结果,避免不必要的加固和限行。
| [1] | STEWART M G,VAL D V.Role of Load History in Reliability-based Decision Analysis of Aging Bridges[J]. |
| [2] | 李全旺,王草,张龙.考虑结构劣化和荷载历史的既有桥梁承载力更新[J].清华大学学报:自然科学版,2015,55(1):8-13.LI Quan-wang,WANG Cao,ZHANG Long.Updating for Bearing Capacity of Existing Bridges Considering Structural Deterioration and Loading History[J].Journal of Tsinghua University:Science and Technology Edition,2015,55(1):8-13. |
| [3] | 李全旺,李春前,孙健康.基于结构可靠性理论的既有桥梁承载能力评估[J].工程力学,2010,27(增2):142-151.LI Quan-wang,LI Chun-qian,SUN Jian-kang.Reliability Based Capacity Assessment of Existing Bridges[J].Engineering Mechanics,2010,27(S2):142-151. |
| [4] | LAW S S,LI J.Updating the Reliability of a Concrete Bridge Structure Based on Condition Assessment with Uncertainties[J]. |
| [5] | ZHU J S,WU J H.Study on System Reliability Updating through Inspection Information for Existing Cable-stayed Bridges[J].Advanced Materials Research,2011(250/251/252/253):2011-2015. |
| [6] | OKASHA N M,FRANGOPOL D M,ORCESI A D.Automated Finite Element Updating Using Strain Data for the Lifetime Reliability Assessment of Bridges[J]. |
| [7] | FABER M H,VAL D V,STEWART M G.Proof Load Testing for Bridge Assessment and Upgrading[J]. |
| [8] | JTG/T J21-2011,公路桥梁承载能力检测评定规程[S].JTG/T J21-2011,Specification for Inspection and Evaluation of Load-bearing Capacity of Highway Bridge[S]. |
| [9] | HALL W B.Reliability of Service-proven Structures[J]. |
| [10] | MORI Y,ELLINGWOOD B R.Reliability-based Service-life Assessment of Aging Concrete Structures[J]. |
| [11] | ENRIGHT M P,FRANGOPOL D M.Service-life Prediction of Deteriorating Concrete Bridges[J]. |
| [12] | BECK J L,KATAFYGIOTIS L S.Updating Models and Their Uncertainties.I:Bayesian Statistical Framework[J].Journal of Engineering Mechanics,1998,124(4):455-461. |
| [13] | 李庆扬,王能超,易大义.数值分析[M].北京:清华大学出版社,2008.LI Qing-yang,WANG Neng-chao,YI Da-yi.Numerical Analysis[M].Beijing:Tsinghua University Press,2008. |
| [14] | 易建国.桥梁计算示例集:混凝土简支梁(板)桥[M].北京:人民交通出版社,1991.YI Jian-guo.Illustrative Examples of Bridge Calculation for Concrete Simply Supported Beam(Plate) Bridges[M].Beijing:China Communications Press,1991. |
| [15] | JTG D62-2004,公路钢筋混凝土及预应力混凝土桥涵设计规范[S].JTG D62-2004,Code for Design of Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts[S]. |
| [16] | ELLINGWOOD B.Development of a Probability Based Load Criterion for American National Standard A58:Building Code Requirements for Minimum Design Loads in Buildings and Other Structures[M].Washington,D.C.:US Department of Commerce,1980. |
| [17] | GB/T 50283-1999,公路工程结构可靠度设计统一标准[S].GB/T 50283-1999,Unified Standard for Reliability Design of Highway Engineering Structures[S]. |
| [18] | 孙晓燕,王海龙.超载运营下服役钢筋混凝土桥梁疲劳损伤研究[J].应用基础与工程科学学报,2008,16(5):733-740.SUN Xiao-yan,WANG Hai-long.Fatigue Damage Analysis on Existing Reinforced Concrete Bridge under Overloading[J].Journal of Basic Science and Engineering,2008,16(5):733-740. |
 2016, Vol. 31
2016, Vol. 31
