扩展功能
文章信息
- 王修勇, 韩湘逸, 孙洪鑫, 李寿科
- WANG Xiu-yong, HAN Xiang-yi, SUN Hong-xin, LI Shou-ke
- 琼州海峡跨海大桥桥址处风雨联合概率分布研究
- Research of Wind Velocity and Rainfall Joint Probability Distribution at Qiongzhou Strait Bridge Site
- 公路交通科技, 2016, Vol. 31 (2): 60-66
- Journal of Highway and Transportation Research and Denelopment, 2016, Vol. 31 (2): 60-66
- 10.3969/j.issn.1002-0268.2016.02.010
-
文章历史
- 收稿日期: 2015-07-16
随着经济社会的快速发展,我国多个跨海超级工程开始规划和建设。在服役期内,跨海大桥将不可避免地受到超级台风的作用,而台风发生过程中往往伴随大量降水,风雨的耦合作用可能对桥梁产生不利影响。因此,确定在极端气候条件下的极值降雨量和极值风速等参数,对跨海工程的规划设计和安全运营具有非常重要的意义。
在降雨对结构作用研究方面,已有一些学者研究了降雨对桥梁结构气动力的影响,辛大波等[1, 2]研究了大跨桥梁在风雨联合作用下的颤振稳定性和风雨致涡激振动问题,结论显示:降雨对大跨桥梁的颤振导数和颤振临界风速都存在影响;降雨增大了桥梁主梁涡激振动幅值。陶仕博等[3]通过风洞实验室中的风雨联合作用试验系统分析了不同风速和雨强组合作用下节段模型的静力三分力,结果表明:节段模型阻力系数随雨强增大而增大。但都是在较小风速和雨量条件下进行,而在实际沿海地区极值气候条件下的极值雨量和极值风速却大得多,为了研究更符合实际条件结构风、雨耦合效应,需要统计分析当地风速、雨强的联合概率分布。在风、雨参数研究方面,国内外有许多学者对风速和雨量进行现场实测[4, 5],周俊华[6]对中国台风灾害的研究显示:大风暴雨叠加的极端气候条件下,风速和雨量之间呈现较高的正相关性,即风速随雨量增大而增大。在风、雨联合概率模型研究方面,武占科[7]用Gumbel Copula函数联合概率模型和极值Ⅰ型联合概率分布模型描述了年极值风速和年极值雨量两随机变量,但没有对联合分布的重现期研究做进一步的探讨。近些年来,Copula函数被作为多变量联合概率分布的工具广泛应用于金融和水文领域,陈子燊等[8, 9]用Copula函数研究汕尾海域极值波高与风速的关系,还有很多关于洪水或干旱出现概率方面的研究[10, 11, 12, 13, 14]。
本文根据Copula函数的理论和方法,利用琼州海峡大桥桥址实测数据和澄迈气象站历史数据建立了风雨联合概率模型,深入分析了风速、雨量之间的概率分布特征,并对风速、雨量重现期进行了研究。
1 风雨联合概率分布理论 1.1 二元Copula函数联合概率模型Copula函数描述的是变量间的相关性,实际上是一类将联合分布函数与它们各自的边缘分布函数连接在一起的函数,是一种连接函数。根据Copula函数的特性,建立风速与雨量联合概率模型可分为两步,首先分别确定风速与雨量最优边缘分布FX(x)和FY(y),然后选择最优Copula函数来构建变量间相关结构。当前应用较为普遍的是Archimedean型Copula函数,该函数是由其生成元唯一确定的单参数函数。Archimedean Copula型函数包括Gumbel-Copula函数、Clayton Copula 函数及Frank Copula 函数等,其概率分布、概率密度及其特征如下:
对于Gumbel-Copula函数,其概率分布:

式中u=FX(x),v=FY(y)分别为风速、雨量的最优边缘分布;α为Copula参数。Gumbel-Copula函数相应的概率密度为:

Gumbel Copula函数的生成元φ(t)为:φ(t)=(-Ιnt)θ,该函数适用于变量存在正相关的情形,主要刻画随机变量间的上尾相关性。
对于Clayton Copula 函数,其概率分布和概率密度分别为:

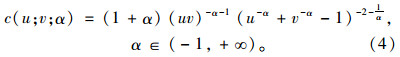
Clayton Copula 函数的生成元φ(t)为:φ(t)=(t-α-1)/α,该函数适用于正相关性随机变量,主要用来描述联合分布中随机变量间的下尾相关性。
对于Frank Copula 函数,其概率分布和概率密度分别为:
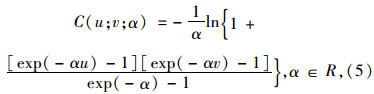
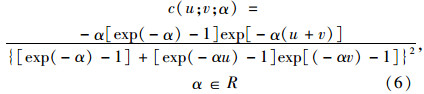
Frank Copula函数其生成元φ(t)为: φ(t)=-ln[(e-θt-1)/(e-θ-1)],该函数能描述正或负相关的随机变量,结构具有对称性,在其分布的上尾和下尾,变量间的相关性呈对称增长。
Copula参数α的估计方法有相关性指标法、适线法和极大似然法等3种,根据相关性指标法,Copula参数α可由Kendall秩相关系数τ与α的关系间接求得。Kendall秩相关系数τ可采用直接估计法得到。秩相关系数τ与α关系为:

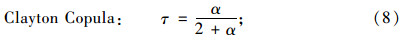

式中 为Debye函数。
为Debye函数。
不同的Copula函数得到了不同的联合概率模型,我们可以通过如下拟合优度评价方法来判定最优Copula函数:Genest-Rivest图示法、均方根误差准则法和AIC信息准则法等。本文采用均方根误差法评价Copula函数,即计算各个Copula函数与经验Copula函数之间的欧式平方距离,距离越小,拟合程度越优。
1.2 风雨联合概率分布与重现期根据Copula函数的性质,极值风速x和对应极值降雨量y的联合分布可表示为:
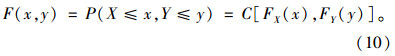
根据风速、雨量的边缘分布可知,极值风速x和极值雨量y的重现期分别为:
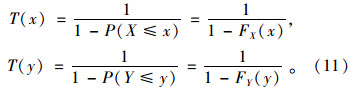
联合重现期T0表示事件中风速变量X或雨量变量Y超过某一特定值,即二者中只要有一个超过某一特定值的重现期;同现重现期Ta表示事件中风速变量X与雨量变量Y都超过某一特定值,即二者要同时达到的重现期。联合重现期T0和同现重现期Ta计算公式分别为:
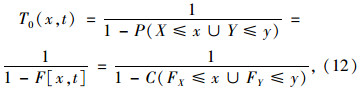
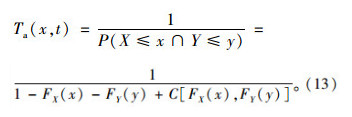
由以上公式可得:
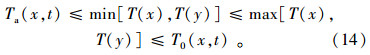
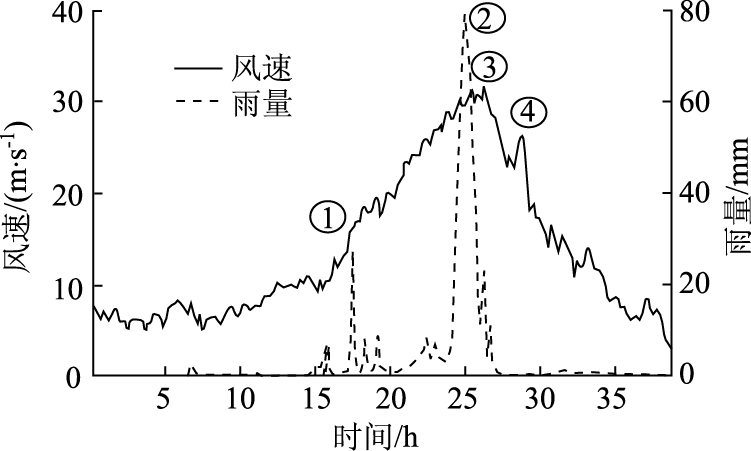
为了获得琼州海峡大桥桥址风、雨特征参数,2012年在桥址南岸及北岸建立了风、雨现场观测系统,南岸系统如图 1所示。 该系统南岸测风塔高65 m,在离地10,20,40,60 m处各安装一台英国某公司生产的超声风速仪和一台美国某公司生产的螺旋桨式风速仪,在塔工作平台上安装一台雨量计。现场观测系统在2012年8月至2014年8月期间共完整观测到“启德”、“海燕”、“威马逊”等9个台风,根据9个台风中的10 min平均风速极值和小时雨量极值,提取出了36组风速X、雨量Y极值观测数据。图 2为台风“威马逊”的平均风速、雨量时程图,本文选取了雨量极值点①、②和风速极值点③、④作为样本点,提取出每个样本点的平均风速值和小时降雨量值作为数据样本。样本中最大10 min 风速为31.87 m/s,最大降雨量为340 mm/h。为了对比桥址处极值风速、雨量,选取了离海岸线28 km的澄迈气象站(离观测塔位置最近的气象站)1984年至2013年的年最大10 min平均风速与年最大日降雨量进行对比研究,气象站样本中最大风速为20 m/s,最大降雨量为313 mm/d。从两组极值样本数据可知,澄迈观测站的风速、雨量数据明显小于桥址观测塔的观测值。

|
| 图 1 琼州海峡大桥桥址观测站布置图 Fig. 1 Arrangement of observation station at Qiongzhou Strait Bridge site |
|
| 图 2 台风“威马逊”的平均风速与雨量时程图 Fig. 2 Time histories of average wind speed and rainfall caused by ‘Rammasun’ typhoon |
设近地层的平均风速、雨量为平稳随机过程,使用MATLAB基于正态核函数的方法计算出风速、雨量的概率密度分布,并用最小二乘法对概率密度分布进行拟合。采用极值Ⅰ型概率分布表示其特征。其概率分布函数和概率密度函数分别为:
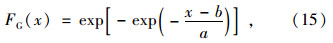

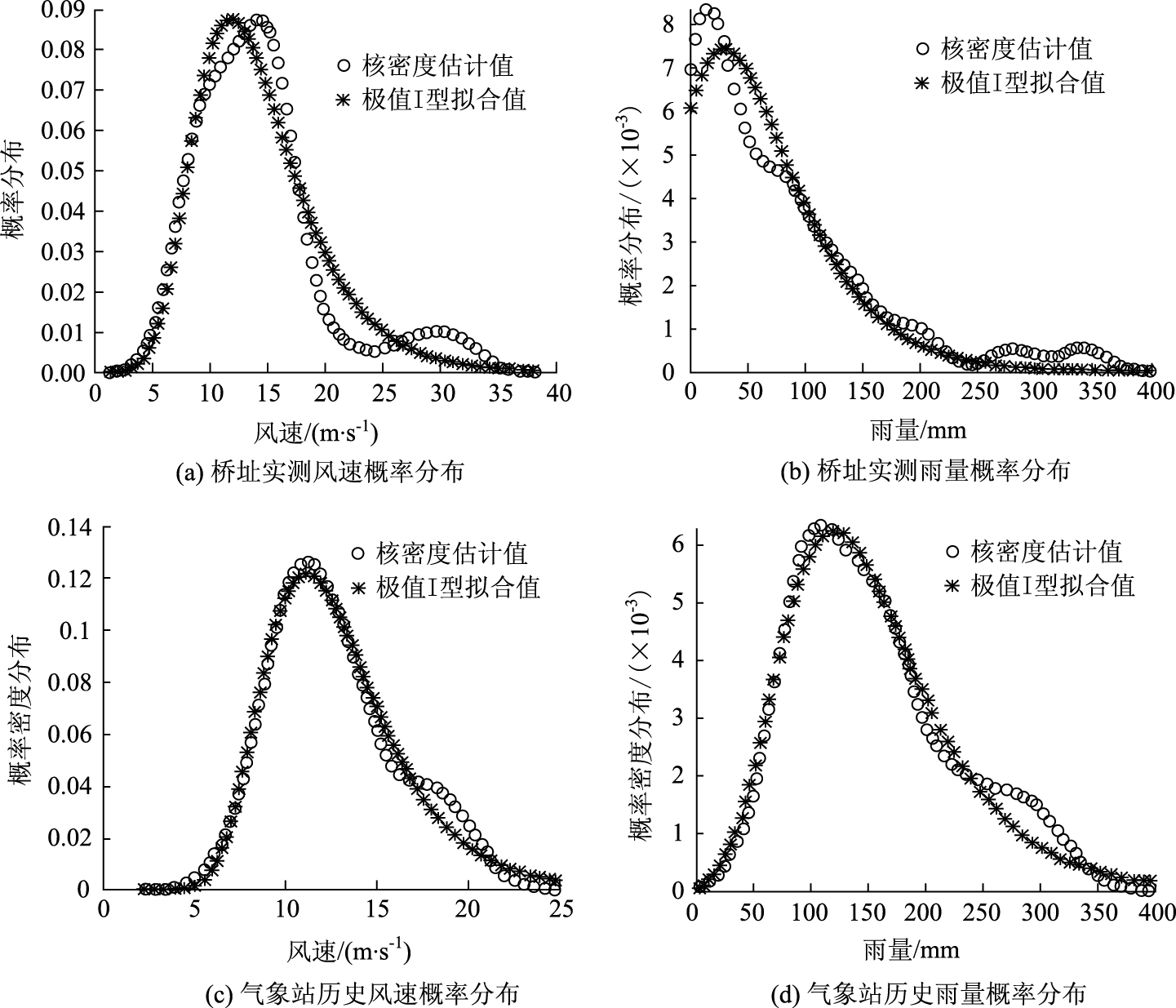
式中a,b为极值Ⅰ型概率分布特征参数,根据样本数据采用最小二乘法拟合求取,得到观测塔和气象站风速与雨量的相应参数如表 1所示。风速与雨量概率密度的核密度估计图和拟合的极值Ⅰ型概率分布曲线如图 3所示,从图可看出核密度估计曲线与极值Ⅰ型分布拟合较好。
| 拟合参数 | a | b |
| 观测塔(风速) | 42.174 | 11.779 6 |
| 观测塔(雨量) | 49.334 1 | 29.471 2 |
| 澄迈气象站(风速) | 3.062 5 | 11.139 1 |
| 澄迈气象站(雨量) | 59.020 5 | 119.739 7 |
|
| 图 3 边缘分布拟合曲线图 Fig. 3 Fitting curves of margin distribution |
根据样本数据,用直接估计法可以得到Kendall秩相关系数τ,获得的相关系数如表 2所示。由相关系数求得Copula函数参数α如表 3所示。计算出上述Copula函数各自的参数后,引入经验Copula模型对各个模型实测数据拟合优度进行评价,3种Copula函数的平方欧氏距离如表 4所示。从表 4可知,对桥址观测塔风速与雨量联合概率分布拟合最好的为Gumbel Copula函数,澄迈气象站的风速与雨量联合概率分布拟合最好的为Clayton Copula函数。
| 数据来源 | 观测塔 | 澄迈气象站 |
| Kendall秩相关系数τ | -0.093 7 | 0.142 2 |
| Copula函数类型 | 桥址观测塔观测 | 澄迈气象站观测 |
| Gumbel Copula | 1.063 4 | 1.217 5 |
| Clayton Copula | -0.424 5 | 1.623 9 |
| Frank Copula | 1.450 9e-06 | 0.574 9 |
| Copula函数类型 | 桥址观测塔观测 | 澄迈气象站观测 |
| Gumbel Copula | 0.005 3 | 0.009 2 |
| Clayton Copula | 0.014 2 | 0.008 5 |
| Frank Copula | 0.008 1 | 0.011 |
桥址观测站和澄迈气象站的风雨联合概率分布密度和联合概率分布分别如图 4~图 6所示。从图中可以看出,桥址观测站风速、雨量联合概率分布基本一致,桥址观测站风速、雨量极值明显大于澄迈气象站。

|
| 图 4 桥址观测塔风速与雨量联合概率密度模型 Fig. 4 Joint probability density model of wind speed and rainfall at bridge observation tower |

|
| 图 5 澄迈气象站位置风速与雨量联合概率密度模型 Fig. 5 Joint probability density model of wind speed and rainfall at Chengmai weather station |

|
| 图 6 风速与雨量联合概率分布模型 Fig. 6 Joint probability distribution model of wind speed and rainfall |
根据桥址观测站和澄迈气象站数据得到的风雨联合重现期等值线和同现重现期等值线分别如图 7、图 8所示,可以看出,风速、雨量联合重现期小于边缘分布重现期,边缘分布重现期则又小于联合分布重现期。由于两组数据的采集位置不同,雨量单位也不同(观测塔的单位为mm/h,气象站的单位为mm/d),只能用于参照对比。在图中可以发现,观测塔位置处的联合重现期等值线对应的风速、雨量均比气象站位置的大,其中观测塔处风速比气象站处设计风速大72%~95%。

|
| 图 7 联合重现期(年)等值线图 Fig. 7 Annual contours of joint return period |
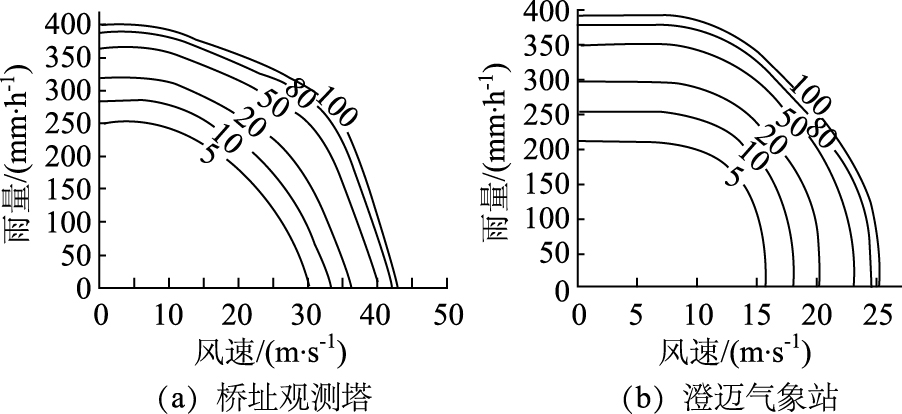
|
| 图 8 同现重现期(年)等值线图 Fig. 8 Annual contours of occurrence return period |
不同重现期的设计风速和设计雨量见表 5。从表中可知,当平均风速为43.39 m/s,小时降雨量为399.24 mm时对应的各自边缘分布重现期均为100 a,但对应的联合重现期为65.3 a,对应的同现重现期为213.7 a。
| 重现期/a | 边缘分布设计值 | |||
| T | T0(x,y) | Ta(x,y) |
风速/ (m·s-1) |
雨量/ (mm·h-1) |
| 100 | 65.3 | 213.7 | 43.39 | 399.24 |
| 80 | 52.2 | 171 | 42.45 | 388.23 |
| 50 | 32.7 | 106.9 | 40.47 | 365.03 |
| 20 | 13.1 | 42.7 | 36.6 | 319.79 |
| 10 | 6.5 | 21.3 | 33.67 | 285.52 |
| 5 | 3.3 | 10.6 | 30.73 | 251.19 |
边缘分布计算出的重现期风速、雨量值小于联合分布重现期的计算值,随重现期的增大,二者差值有减小的趋势。
4 结论本文基于二元Copula函数联合概率模型,根据琼州海峡大桥桥址观测站实测数据和澄迈气象站历史数据,建立了风速和对应雨量的风雨联合概率分布模型,并对联合重现期和同现重现期进行了研究。得到以下结论:
(1)风速、雨量符合极值Ⅰ型分布;
(2)采用二元Copula函数建立风速、雨量两变量联合概率分布模型,桥址观测塔处数据的拟合最优连接函数为Gumbel Copula函数,澄迈气象站数据的拟合最优连接函数为Clayton Copula函数;
(3)利用联合概率分布模型,能对风速、雨量联合重现期和同现重现期进行预测,为工程设计提供参数;
(4)桥址观测站获得的极值风速、雨量比澄迈气象站的观测数值大得多,为了准确确定桥址风、雨设计参数,在桥址处建立观测系统具有重要意义。
| [1] | 辛大波,王亮,欧进萍,等.风雨联合作用下大跨桥梁颤振稳定性试验研究[J].土木工程学报,2012,45(3):110-115.XIN Da-bo,WANG Liang,OU Jin-ping,et al.Experimental Study on the Flutter Stability of Long-span Bridges Subjected to Wind and Rain[J].China Civil Engineering Journal,2012,45(3):110-115. |
| [2] | 辛大波,张明晶,王亮,等.大跨度桥梁主梁风雨致涡激振动试验研究[J].哈尔滨工程大学学报,2011,32(9),1168-1172.XIN Da-bo,ZHANG Ming-jing,WANG Liang,et al.Experimental Study on Wind-rain-induced and Vortex-induced Vibration in Bridge Deck Sections of Long-span Bridges[J].Journal of Harbin Engineering University,2011,32(9):1168-1172. |
| [3] | 陶世博,辛大波,欧进萍.桥梁主梁风雨致静力试验研究[J].钢结构,2011,26(5),23-25.TAO Shi-bo,XIN Da-bo,OU Jin-ping.Researen on the Wind-rain Induced Static Force on a Bridge Deck[J].Steel Construction,2011,26(5),23-25. |
| [4] | BLOCKEN B,CARMELIET J.A Review of Wind-driven Rain Research in Building Science[J]. |
| [5] | CHOI E C C.Wind-driven Rain and Rriving Rain Coefficient during Thunderstorms and Non-Thunderstorms[J].Journal of Wind Engineering and Industrial Aerodynamics,2001,89(3/4):293-308. |
| [6] | 周俊华.中国台风灾害综合风险评估研究[D].北京:北京师范大学,2004.ZHOU Jun-hua.Risk Assessment of Typhoon Disasters in China[D].Beijing:Beijing Normal University,2004. |
| [7] | 武占科,赵林,葛耀君.上海地区台风条件风速和雨强联合概率分布统计[J].空气动力学学报,2010,28(4):393-399.WU Zhan-ke,ZHAO Lin,GE Yao-jun.Statistical Analysis of Wind Velocity and Rainfall Intensity Joint Probability Distribution of Shanghai Area in Typhoon Condition[J].Acta Aerodynamica Sinica,2010,28(4):393-399. |
| [8] | 陈子燊.波高与风速联合概率分布研究[J].海洋通报,2011,30(2):159-164.CHEN Zi-shen.Study on Joint Probability Distribution of Wave Height and Wind Velocity[J].Marine Science Bulletin,2011,30(2):159-164. |
| [9] | 陈子燊,曹深西.基于Copula函数的波高与周期长期联合分布[J].海洋通报,2012,31(6):630-635.CHEN Zi-shen,CAO Shen-xi.Long-term Joint Distribution of Wave Height and Period Based on Copula Functions[J].Marine Science Bulletin,2012,31(6):630-635. |
| [10] | 方彬,郭生练,肖义,等.年最大洪水两变量联合分布研究[J].水科学进展,2008,19(4):505-511.FANG Bin,GUO Sheng-lian,XIAO Yi,et al.Annual Maximum Flood Occurrence Dates and Magnitudes Frequency Analysis Based on Bivariate Joint Distribution[J].Advances in Water Science,2008,19(4):505-511. |
| [11] | 倪增华,刘合香,罗彦丽,等.Copula函数在广西洪涝灾害的降水概率预测中的应用[J].气象研究与应用,2014,35(2):32-39.NI Zeng-hua,LIU He-xiang,LUO Yan-li,et al.Copulas Application in Precipitation Probability Forecast of Flood Disasters in Guangxi[J].Journal of Meteorological Research and Application,2014,35(2):32-39. |
| [12] | 谢华,罗强,黄介生.基于三维copula函数的多水文区丰枯遭遇分析[J].水科学进展,2012,23(2):186-193.XIE Hua,LUO Qiang,HUANG Jie-sheng.Synchronous Asynchronous Encounter Analysis of Multiple Hydrologic Regions Based on 3D Copula Function[J].Advance in Water Science,2012,23(2):186-193. |
| [13] | 周念清,赵露,沈新平.基于Copula函数的洞庭湖流域水沙丰枯遭遇频率分析[J].地理科学,2014,34(2):242-248.ZHOU Nian-qing,ZHAO Lu,SHEN Xin-ping.Copula Based Probability Evaluation of Rich-poor Runoff and Sediment Encounter in Dongting Lake Basin[J].Scientia Geographica Sinica,2014,34(2):242-248. |
| [14] | 徐琨,陆宝宏,汪集旸,等.基于Copula函数的拓林水库设计洪水频率分析[J].水电能源科学,2014,32(8):61-64.XU Kun,LU Bao-hong,WANG Ji-yang,et al.Design Flood Frequency Analysis of Zhelin Reservoir Based on Copula Functions[J].Water Resources and Power,2014,32(8):61-64. |
 2016, Vol. 31
2016, Vol. 31
