扩展功能
文章信息
- 冉茂平, 肖旺新, 周兴林, 张云, 谢旭飞
- RAN Mao-ping, XIAO Wang-xin, ZHOU Xing-lin, ZHANG Yun, XIE Xu-fei
- 基于三维分形维数的沥青路面抗滑性能研究
- Research of Skid Resistance of Asphalt Pavement Based on 3D Fractal Dimension
- 公路交通科技, 2016, Vol. 31 (2): 28-32
- Journal of Highway and Transportation Research and Denelopment, 2016, Vol. 31 (2): 28-32
- 10.3969/j.issn.1002-0268.2016.02.005
-
文章历史
- 收稿日期: 2014-12-14
2. 交通运输部公路科学研究院, 北京 100088
2. Research Institute of Highway, Ministry of Transport, Beijing 100088, China
研究发现,沥青路面抗滑性能的好坏对道路使用安全性非常重要。目前一般认为沥青路面抗滑性能是由沥青混合料颗粒间的宏观构造深度和集料表面自身的微观构造两方面提供。大量研究证明[1, 2],沥青路表的微观构造对抗滑能力的贡献较大。由于沥青路面微观纹理呈现出相似性或自仿射性,因此许多学者采用分形理论对沥青路面微观纹理进行量化,取得了一定的成果[3, 4, 5, 6]。但大多数对沥青路面微观纹理的分形计算都借助数字图像处理技术,且基于二维分形,不直观。基于此,本文采用改进的立方体覆盖法,在获取路面三维微观形貌的基础上计算路表微观构造的三维分形维数,并与摆式摩擦仪进行对比,分析分形维数与抗滑性间的关系。
1 分形理论分形理论(Fractal Theory)是由数学家芒德勃罗(B.B.Mandelbrot)首先提出。在20世纪,分形理论被广泛应用于数学、物理、材料、计算机科学等领域中。分形具有以下特征[6]:
(1)精细的机构,即有任意比例的细节;(2)不规则性,无论整体还是局部都不能用欧式几何来描述;(3)某种形式的自相似性。
目前,对分形的判断常采用自相似分形的幂律定义:
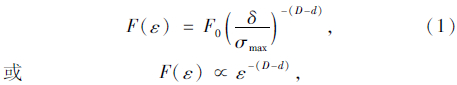
式中,F(ε)为某一几何图形的长度、面积或体积;F0为几何图形为整形(D=1)时的长度、面积或体积;δ为长度尺码;ε为无量纲尺码长度;D为分形维数;d为分形的拓扑维数,d=1是分形曲线,d=2是分形曲面,d=3是三维分形体。
如果采用边长为δ的正方形盒子去对F图像进行覆盖时,所需盒子数为Nδ(F)满足式(2)幂律,则认为它是一个分形:

维数是分形几何的中心概念,它表明一个集合占据的空间大小。在分形中,它对图形的准确描述起着重要的作用。分形维数是判断两个分形是否一致的度量标准之一。分形维数可用计盒维数来表示。计盒维数定义如下:设事物F是n维空间Rn上非空的有界子集,使用最大直径δ的盒子去覆盖事物F,最少的盒子个数为Nδ(F),则事物F的上、下盒维数定义为:

若式(3)两值相等,则这个值即为F的计盒维数,记为:
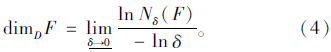
式中,D为计盒维数;Nδ(F)为包含信息的盒子数;δ为立方体三维网格边的长度。
通过分形理论计算集合F的计盒维数时,首先应构造一些边长为δ的立方体方形盒子,然后用不同δ盒子去覆盖集合F,统计出相应的盒子数Nδ(F),最后分维数可以用双对数坐标中图形的斜率来进行估计。
2 沥青路面三维分形维数计算沥青混凝土由粗骨料、细骨料、沥青等组成,其表面凹凸分布具有自相似性的分形特征,因此沥青路面表面就是一种分形[7, 8]。在获取沥青路面三维微观形貌基础上,使用改进的立方体覆盖法去覆盖无规则沥青路表三维曲面,即可计算其三维分维数。改进的立方体覆盖法与传统立方体覆盖法的计算步骤相似,最大区别在于:在每个网格中,用设置的立方体网格去覆盖物体表面时,传统立方体覆盖法的起始位置是从最低角点的高度处开始,而改进的立方体覆盖法则从一个统一的高度覆盖,由于覆盖的起始位置不同,覆盖物体表面的立方体个数也不同。改进的立方体覆盖法从统一的基准面开始覆盖,有效地避免了覆盖过程中的人为因素,更加真实地反映了物体表面粗糙信息,是盒子数覆盖法计算曲线分形维数向计算曲面分形维数的扩展,非常适合计算沥青路面三维分形维数。
采用改进的立方体覆盖法计算沥青路面三维分形维数步骤如下[9, 10, 11, 12, 13]:
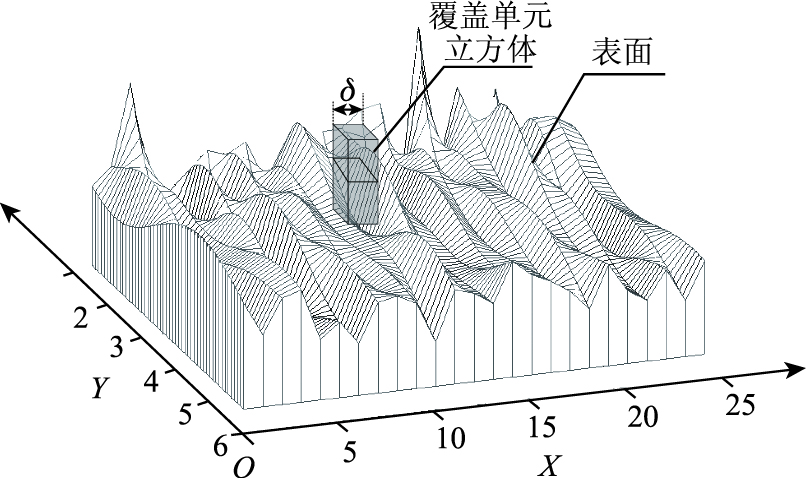
(1)在已获取的沥青路面三维微观构造(如图 1所示)的基础上,在二维XOY平面上方放置一个立方体网格,设置立方体网格体的尺寸为δ。
|
| 图 1 改进的立方体覆盖法 Fig. 1 Improved cubic covering method |
(2)立方体网格的底部4个顶点对应的4个高度分别为h(i,j),h(i+1,j),h(i,j+1),h(i+1,j+1),其中,1≤i,j≤n-1,n为每个边的量测点数。使用立方体δ对曲面体进行覆盖,统计出覆盖表面区域δ×δ内的立方体个数,在第i,j网格内立方体个数Ni,j有:
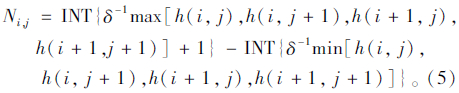
(3)统计覆盖整个物体表面所需的立方体总数N(δ):
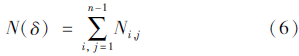
(4)根据分形理论,覆盖整个物体表面所得立方体数N(δ)与尺度δ之间关系[9, 10]为:

由式(7)可得分形维数D:
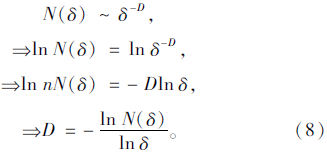
(5)改变小立方体的尺度大小再次去覆盖,依次计算所需的立方体总数,最后分维数可以用双对数坐标中图形的斜率来进行估计。
3 沥青路面三维分形维数与路面抗滑性关系研究本次试验选取路面几种常用集料制成的沥青试块进行试验,在获取不同试件的三维微观形貌后,运用改进的立方体覆盖法计算不同沥青试件表面的三维分形维数,并与摆式摩擦仪测得的摩擦系数进行对比分析,分析路表三维分形维数与摩擦系数之间的关系。
3.1 试验材料与仪器 3.1.1 试验材料选取4种沥青路面常用石料,分别编号为A,B,C,D,沥青为SBS改性沥青,矿粉为石灰石矿粉,级配采用AC-16,采用旋转压实仪对沥青混合料压实成型,每种石料成型1个试件,每个试件测量5个不同的部位。几种成型试件见图 2所示。

|
| 图 2 四种沥青混合料试件 Fig. 2 Four types of asphalt mixture test specimen |
为了较真实地模拟路面情况,对成型试件采用交通运输部公路科学研究院改性沥青与铺面工程技术研发部自主研发的平板式磨光机对试件进行磨损,在压力为0.3 MPa,频率为20 Hz的条件下磨损1 h。用InfinitFocus自聚焦三维表面测量仪器获取4种试件的三维形貌,并用摆式仪器测得试件的摩擦系数。
3.2 三维分形维数与摆值提取利用InfinitFocus自聚焦三维显微仪配套软件,可获取试样表面的真实信息和高度信息如图 3所示。本文主要利用试样的高度信息,然后在此基础上,采用改进的立方体覆盖法对4个试件5个不同测量部位的分形维数进行计算,同时用摆式摩擦仪测量其摩擦系数,结果如表 1所示。

|
| 图 3 试样表面真实信息与高度信息 Fig. 3 Real information and altitude information of test specimen surface |
| 测量部位 | 试件类型 | |||||||
| A试件 | B试件 | C试件 | D试件 | |||||
| 分形维数D | 摩擦系数F | 分形维数D | 摩擦系数F | 分形维数D | 摩擦系数F | 分形维数D | 摩擦系数F | |
| 1 | 2.69 | 0.94 | 2.38 | 0.85 | 2.29 | 0.74 | 2.11 | 0.68 |
| 2 | 2.59 | 0.87 | 2.25 | 0.75 | 2.15 | 0.68 | 2.10 | 0.65 |
| 3 | 2.63 | 0.91 | 2.32 | 0.81 | 2.2 | 0.71 | 2.05 | 0.57 |
| 4 | 2.47 | 0.81 | 2.13 | 0.74 | 2.18 | 0.69 | 2.07 | 0.61 |
| 5 | 2.48 | 0.85 | 2.28 | 0.79 | 2.23 | 0.75 | 2.09 | 0.59 |
| 均值 | 2.57 | 0.88 | 2.27 | 0.79 | 2.21 | 0.71 | 2.09 | 0.62 |
分析表 1数据可知,4种不同集料的沥青试块表面微观构造分形维数的大小关系为: DA > DB > DC > DD,其中试件A与试件B分维数值最大,表现出表面微观形貌比较丰富;4种不同集料的沥青试块表面摩擦系数关系为:FA > FB > FC > FD,可见在相同级配和相同试验条件下,试件A与试件B的表面摩擦系数值越大,所表现出来的微观构造纹理越丰富,反映出来的路用抗滑性就越好。
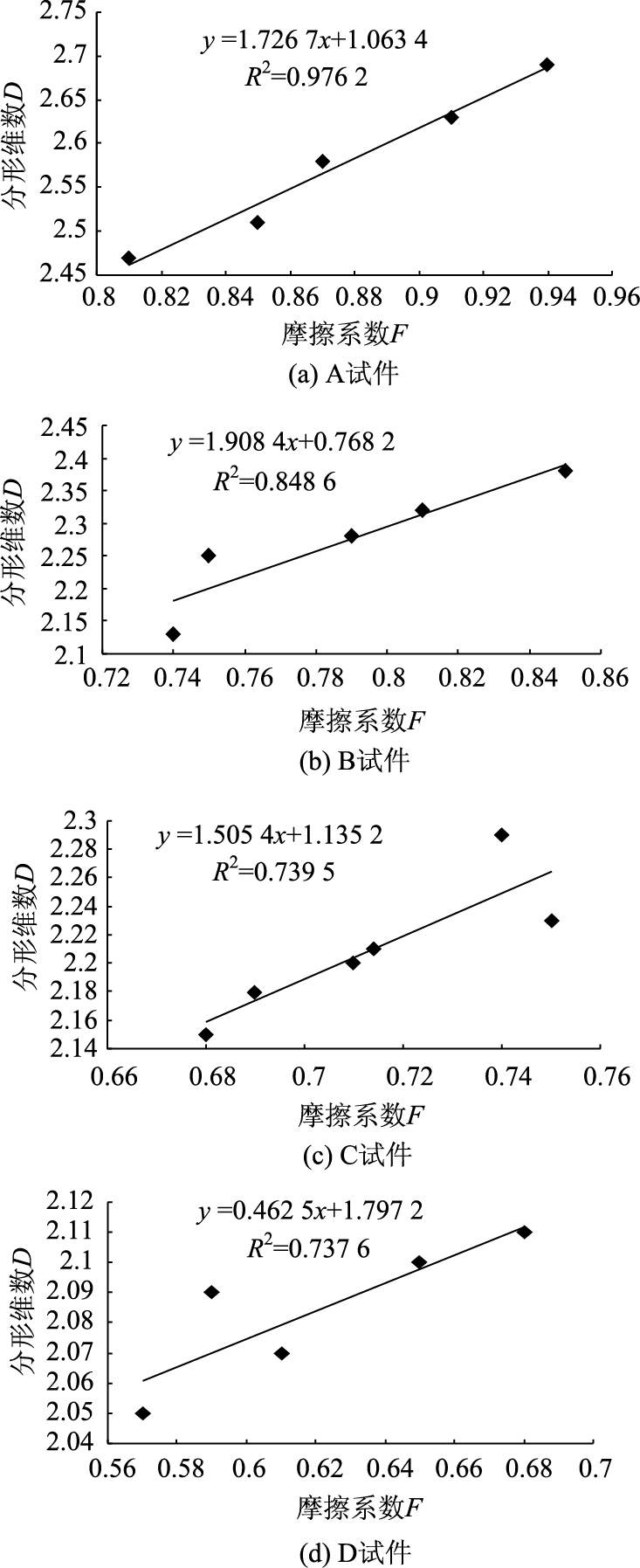
对表 1中不同试件的分形维数与摩擦系数进行统计分析,得到分形维数与摩擦系数之间的相关性分析结果如图 4所示。
|
| 图 4 不同试件分维数D与摩擦系数F的相关性分析 Fig. 4 Correlation analysis of fractal dimension D and friction coefficient F of different specimens |
通过试验数据分析和数理统计得出不同试件表面摩擦系数F与分形维数D的关系如表 2所示。
| 试件类型 | 线性回归公式 | 方程系数R2 |
| A | y=1.726 7x+1.063 4 | 0.976 2 |
| B | y=1.908 4x+0.768 2 | 0.848 6 |
| C | y=1.505 4x+1.135 2 | 0.739 5 |
| D | y=0.462 5x+1.797 2 | 0.737 6 |
由表 1与表 2可知,不同试件表面分形维数D值和摩擦系数值F相互对应,分形维数D大,对应的摩擦系数F也大;试件分形维数D与摩擦系数F有一定的相关性,并不是完全相关。试件A与B的分形维数与摩擦系数相关性相对较好,试件C与D的分形维数与摩擦系数相关性相对较差,其主要原因在于集料种类不同,集料表面的棱角、集料的岩相特性也不尽相同。集料C与D的表面纹理不太丰富,验证了集料表面纹理越丰富,集料的抗滑性能越好的结论。
4 结论在已获得沥青路面微观构造三维图像的基础上,利用改进的立方体覆盖法计算沥青路表微观形貌三维分维数。通过试验论证了分形维数D越大,微观构造越丰富,越利于路面向行车荷载提供稳定和较大的抗滑力;分形维数D值和摩擦系数值F相互对应,分形维数D大,对应的摩擦系数F也大,因此可以利用沥青路表微观构造分维数来分析路面抗滑性能。
| [1] | 孙杨勇.粗集料表面微观构造分形性质与沥青路面抗滑性能关系研究[D].广州:华南理工大学,2010.SUN Yang-yong.Research on Relationship Betweene Coarse Aggregate Surface Micro-structure Fractal Properties and Anti-sliding Performance of Asphalt Pavement[D].Guangzhou:South China University of Technology,2010. |
| [2] | 刘清泉.路用石料的摩擦特性分析[J].中国公路学报,2004,17(3):19-22.LIU Qing-quan.Analysis of Tribological Property of Pavement Stone[J].China Journal of Highway and Transport,2004,17(3):19-22. |
| [3] | 曹平,白秀琴.沥青路表面分形特性与抗滑性能的关系研究[J].润滑与密封,2009,34(3):9-11.CAO Ping,BAI Xiu-qin.Relationship of Fractal Characteristic and Skid Resistance of Asphalt Pavement[J].Lubrication Engineering,2009,34(3):9-11. |
| [4] | 蒋育红,黄宝涛,李家春,等.沥青路面抗滑性能研究[J].武汉理工大学学报:交通科学与工程版,2008,32(4):753-756.JIANG Yu-hong,HUANG Bao-tao.LI Jia-chun,et al.Slip Resistance Performance of Asphalt Mixture[J].Journal of Wuhan University of Technology:Transportation Science & Engineering Edition,2008,32(4):753-756. |
| [5] | 曹平.表面形貌与污染物对沥青路面抗滑性能的影响[D].武汉:武汉理工大学,2009.CAO Ping.Influence of Surface Morphology and Pollutants on Anti-sliding Performance of Asphalt Pavement[D].Wuhan:Wuhan University of Technology,2009. |
| [6] | 李智,刘涛.基于分形理论评价沥青路面微观构造[J].武汉理工大学学报:交通科学与工程版,2013,37(3):501-504.LI Zhi,LIU Tao.Valuation of Microscopic Structure of Asphalt Pavement Based on Fractal Theory[J].Journal of Wuhan University of Technology:Transportation Science & Engineering Edition,2013,37(3):501-504. |
| [7] | 堪文.基于分形理论的环保安全型沥青路面抗滑性能研究[D].西安:长安大学,2013.KAN Wen.Research on Slip Resistance Performance of Environmental Safety Asphalt Pavement Based on Fractal Theory[D].Xi'an:Chang'an University,2013. |
| [8] | 杨彦昌.分形理论在沥青混合料中的应用研究[D].长沙:长沙理工大学,2009.YANG Yan-chang.Research on Application of Fractal Theory in Asphalt Mixture[D].Changsha:Changsha University of Science and Technology,2009. |
| [9] | 周宏伟,谢和平,KWASNIEWSKI M A.粗糙表面分维计算的立方体覆盖法[J].摩擦学学报,2000,20(6):455-459 ZHOU Hong-wei,XIE He-ping,KWASNIEWSKI M A.Fractal Dimension of Rough Surface Estimated by the Cubic Covering Method[J].Tribology,2000,20(6):455-459. |
| [10] | 张亚衡,周宏伟,谢和平.粗糙表面分形维数估算的改进立方体覆盖法[J].岩石力学与工程学报,2005,24(17):3192-3196.ZHANG Ya-heng,ZHOU Hong-wei,XIE He-ping.Improved Cubic Covering Method for Fractal Dimensions of a Fracture Surface of Rock[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(17):3192-3196. |
| [11] | 李学业,刘建峰.图像维数计算方法及其实质研究[J].实验力学,2010,25(2):159-165.LI Xue-ye,LIU Jian-feng.Study of the Calculation Method of True Color Image Dimension and Its Nature[J].Journal of Experimental Mechanics,2010,25(2):159-165. |
| [12] | 姚灿中,杨建梅.复杂网络分形的盒维数改进算法[J].计算机工程与应用,2010,46(8):5-7.YAO Can-zhong,YANG Jian-mei.Improved Box Dimension Calculation Algorithm for Fractality of Complex Networks[J].Computer Engineering and Applications,2010,46(8):5-7. |
| [13] | 张云.基于三维重构的沥青路面微观构造表征技术研究[D].武汉:武汉科技大学,2014.ZHANG Yun.Research on Asphalt Pavement Microstructural Characterization Technique Based on 3D Reconstruction[D].Wuhan:Wuhan University of Science and Technology,2014. |
 2016, Vol. 31
2016, Vol. 31
