扩展功能
文章信息
- 夏荣霞, 吴德华, 何杰, 翁辉, 史登峰
- XIA Rong-xia, WU De-hua, HE Jie, WENG Hui, SHI Deng-feng
- 平曲线处大型客车最大安全运行速度计算模型研究
- Research on Calculation Model of Maximum Safe Driving Speed of Coach at Highway Horizontal Curve
- 公路交通科技, 2016, Vol. 31 (1): 140-146
- Journal of Highway and Transportation Research and Denelopment, 2016, Vol. 31 (1): 140-146
- 10.3969/j.issn.1002-0268.2016.01.022
-
文章历史
- 收稿日期: 2014-12-14
2. 东南大学交通学院, 江苏 南京 210096;
3. 浙江省交通规划设计研究院, 浙江 杭州 310006
2. School of Transportation, Southeast University, Nanjing Jiangsu 210096, China;
3. Zhejiang Provincial Institute of Communications Planning, Design and Research, Hangzhou Zhejiang 310006, China
由汽车行驶理论可知,汽车行驶的纵向稳定性优于横向稳定性,对于转弯的车辆更是如此。而据道路交通事故统计,60%以上的交通事故发生在曲线处,其中,与大型车辆相关的事故又占到了曲线段事故总数的90%以上,进一步分析可知大型车辆交通事故形态又以侧翻、侧滑为主[1]。而对于出现的侧滑现象(推头、甩尾、原地打转)中,由车辆的动力学特性可知,往往后轮侧滑带来的危险性更大。针对车辆的弯道行驶问题,国内外学者开展了各方面的研究,东南大学的游克思等[2]采用Matlab/Simulink建立了3自由度动力学模型,分析弯道路段几何参数对车辆操纵稳定性的影响。S. K. Rao[3]将弯道划分为独立单元,研究弯道的线形设计,对弯道的一些重要参数进行了分析。
然而,以上弯道行驶安全方面的问题研究以及现行的道路平曲线半径计算模型只是针对小型客车的动力学特性来分析的,而没有考虑大型车辆的运动学特性,这也可能是导致在平曲线处大型车辆事故多发的原因之一。相对于小型车辆而言,大型车辆具有轴距长、载重大、轴载分配不均匀、机动性能相对较差等特征。而相比于大型货车,大型客车一般载有大量旅客,甚至出现超载现象且乘客对车辆速度和舒适性的要求,车速较大、车辆重心较高。一旦发生事故,其后果尤为严重,故论文选择大型客车作为研究对象,分析其在道路平曲线处的受力状况,推算其在道路平曲线处的最大安全运行速度,最终给出基于大型客车的道路平曲线处运行速度的预测模型。这对分析驾驶员在转弯处的驾驶舒适性和乘客的乘坐安全舒适性,保障道路平曲线处大型客车的行车安全有着重要的意义。
1 圆曲线与安全行车速度的关系道路设计中,平曲线半径、超高设计等指标是通过分析平曲线半径、横向超高与车辆行驶速度之间关系获取,我国道路勘测教材和公路工程技术标准[4, 5],都是依据式(1)来确定最大行驶速度所对应的最小平曲线半径和超高的,即最小平曲线半径对应的最大行驶速度。

式(1)在推算车辆行驶速度和平曲线半径间关系时,做了如下假设:
(1) 将车辆简化成了一个质点进行推算;
(2)前后轮轴载分配均匀、横向附着系数一样、四轮完全达到侧滑极限状态。
而实际上,车辆自身存在着机动性,尤其对于大型车辆,由于其轴距较长且轴载分配不均,一般情况下前轴承受的质量小,后轴承受的质量大,经车辆研究人员深入分析发现,后轮驱动的汽车容易产生转向过度,导致后轮发生侧滑,其对车辆的横向稳定性极其不利,极易造成事故的产生[6]。因此,在分析圆曲线最小半径时不仅要考虑前后轴轴载的分配,还需分析前后轴内外侧车轮哪一个更易发生侧滑,进而在分析平曲线半径与车辆最大安全运行速度之间关系时,将车辆自身结构、轮胎磨损等因素考虑进去。
2 基于车路多因素的曲线段车辆最大行驶速度建模分析 2.1 车辆前后轴内外轮受力分析整车悬挂质量GS;前悬挂质量GS1;后悬挂质量GS2;非悬挂质量Gu;前非悬挂质量Gu1;后非悬挂质量Gu2;前钢板弹簧刚度Cφ1;后钢板弹簧刚度Cφ2;轴距L;前轮距B1;后轮距B2;前板簧间距Bs1;后板簧间距Bs2;整车重心高度hg;重心至前轴距离L1;重心至后轴距离L2;前钢板卷耳处至主片中心点连线距地面高度h1;后钢板卷耳处至主片中心点连线距地面高度h2;车轮滚动半径rk。
对车体分别在X方向、Y方向、绕Z方向以及四轮的转动建立七自由度动力学系统模型,由于侧倾角速度δ、横摆角速度γ和侧滑速度v与车辆的前进速度相比均较小,可以忽略它们的乘积项,同时忽略汽车的惯性积、忽略车辆的风阻,得简化的车体运动图[7, 8],如图 1所示。
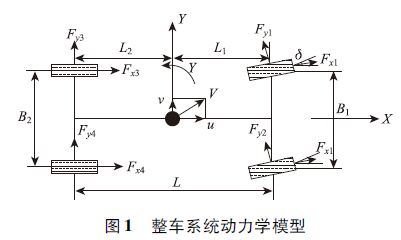 |
| 图 1 整车系统动力学模型 Fig. 1 Vehicle system dynamics model |
汽车转弯行驶,假设悬挂质量侧倾时,前后悬挂的侧倾中心不变,在悬挂质量的中心作用有一个横向力(离心力)并等于GS$\frac{u}{g}$(横向加速度u=0.4g)[9]。
在重心横断面里,横向力作用在侧倾轴上时,前轴内外轮之间载荷再分配为:

悬挂质量的横向力对侧倾轴之矩,引起前轴内外轮之间载荷的再分配为:

假设非悬挂质量的重心在轮心高度,且当后悬挂角刚度较小,承载系统扭转刚度不大时,前轮非悬挂质量的横向力所形成的力矩,使前轴内外轮间的载荷再分配为:

这样,前轴处内外轮之间动载荷再分配总和为:
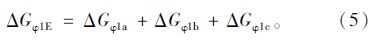
前轴静载分配为:
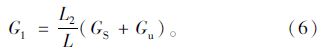
前轴内外轮的总载荷(动、静)为:
前轴内轮

前轴外轮

同理对后轴内外轮:

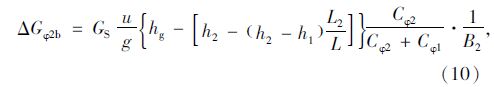
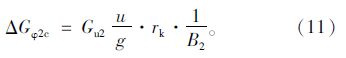
后轴内外轮之间动载荷再分配总和为:
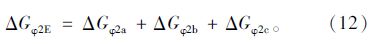
后轴静载分配为:

因此后轴内外轮的总载荷(动、静)为 :
后轴内轮

后轴外轮
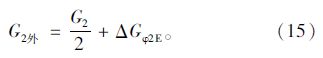
一般L1>L2(大型客车发动机一般后置),得G1内最小,G2外最大。
由计算可确定较易发生侧滑的是前、后轴的内轮,因此论文选择较危险的前、后轴的内轮部分作为研究对象进行分析。
2.2 车辆弯道最大行驶速度的建模分析设车辆转弯过程中,路面超高为α,路面横向摩擦系数为μ,道路设计车速为V,车辆转弯半径为R,侧向力为FY,垂向力为FZ,如图 2所示[10, 11]。
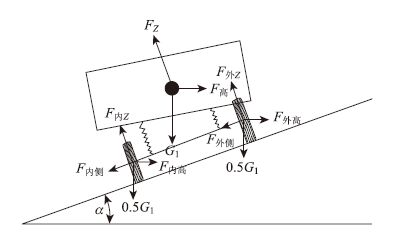 |
| 图 2 1/2车辆模型的受力 Fig. 2 Force analysis of 1/2 vehicle model |
由车辆做圆周运动可知:
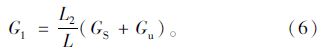
确保车辆不发生侧滑的极限条件为:

超高α比较小时,sinα=α,cosα=1,由式(16)、式(17)得:

对前轴内轮,如图 3所示。
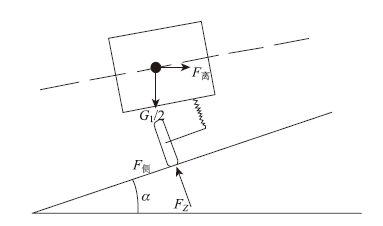 |
| 图 3 1/4车辆模型受力 Fig. 3 Force analysis of 1/4 vehicle model |

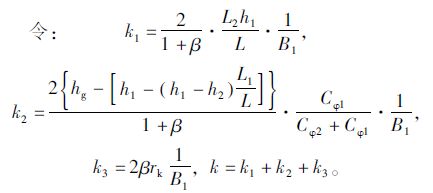
则:

将式(20)代入式(18)最终得:

同理对后轴内轮:


分析计算式(21)、式(22)得:

因此应选V′作为车辆的最大安全运行速度,在确定圆曲线处的最大安全运行速度时应选取车辆后轴内轮为研究对象。
由以上分析可知,当g≤μk时车辆发生侧翻;当g>μk时发生侧滑,且道路圆曲线处汽车发生侧滑的可能性更大。另外由上文分析可知,圆曲线处车辆的最大安全运行速度不仅与道路的性质有关(路面横向力系数、道路超高),与车辆的结构和性质有关(质心高度、质心与前后轴之间的距离、轮距、板簧距、车辆的平顺性等),还与轮胎的特性(车轮的滚动半径,侧偏刚度)有关。总之,车辆的侧滑或侧偏是车-路-轮胎综合作用的结果。
对比上文给出的和现有规范中的圆曲线处的车辆运行速度计算模型,论文给出的模型更能够全面地反映车-路-轮胎综合因素的影响,具有实效性,实际应用效果更强。进一步分析本文提出的模型可知,对于某一类型的车辆[12],其结构是符合特定规范的,也就是说其系数k是一个定值。因此只需对现有的规范模型进行修正,即可得到与本文给出的模型相同的最大安全行驶速度。
3 基于大型客车的圆曲线最大速度分析 3.1 典型配置客车的参数分析在此模型的基础上,选用了一个典型配置的客车——HQ6112A15型客车[9, 13]。该车采用一种当前广为流行的发动机后置的HQ6112A15型长途客车底盘。车长11 m,轴距5.7 m,并仍采用6120QK 型发动机;双片干式液压操纵气助力形式的离合器;全同步器五十铃型变速器;斯太尔型前桥、后桥、传动轴、车架;斯太尔型制动系;悬架系和排气系采用了JT6120结构形式。其整车数据如表 1所示。
| 符号 | 数值 | 符号 | 数值 |
| GS1/N | 38 971 | B2/m | 1.8 |
| GS2/N | 83 797 | Bs1/m | 0.9 |
| Gu1/N | 8 100 | Bs2/m | 0.95 |
| Gu2/N | 14 269 | hg/m | 1.25 |
| C1/(N·m-1) | 202 801 | L1/m | 3.851 |
| C2/(N·m-1) | 562 893 | L2/m | 1.849 |
| rk/m | 0.515 | h1/m | 0.52 |
| B1/m | 2.008 | h2/m | 0.722 |
将车辆的结构参数和动力学参数代入计算得k′=1.1,代入式(22)得V′=$\sqrt {R(g - \mu k')(u + \alpha )} $ 即可计算得到该型号客车在圆曲线一般最小半径、极限最小半径、不设超高的最小半径下的最大安全运行速度。
3.2 基于横向力系数的大型客车圆曲线安全速度值的计算最小的圆曲线半径和侧向摩擦力与超高的分配主要基于侧向加速度的值。对于最小的曲线半径和侧向加速度值由乘客舒适性和行驶稳定性限制[14],表 2给出了横向力系数对汽车行驶稳定性、乘客舒适感的影响[4, 15]。
| 影响项目 | μ值 | 影响程度 | |
| 行驶稳定性 | 0.15~0.16 | 干燥与潮湿路面均可以较高速度安全行驶 | |
| 0.07 | 结冰路面也能安全行驶 | ||
| 乘客舒适 感程度 | |||
| <0.10 | 转弯时感觉不到有曲线存在,很平稳 | μ值最好≤0.10,最大不能超过0.20 | |
| 0.15 | 转弯时略感到有曲线存在,但尚平稳 | ||
| 0.20 | 转弯时已感到曲线存在,并略感到不稳定 | ||
| 0.35 | 转弯时明显感到有曲线存在,并明显感到不稳定 | ||
| ≥0.40 | 转弯时感到非常不稳定,站立不住并有倾倒危险 | ||
为保证行车安全,在进行最大安全行驶速度计算时选取μ=0.07(代表结冰路面);μ=0.10(乘客感觉不到曲线的存在);μ=0.15(代表干燥与潮湿路面车辆行驶稳定,略感到有曲线存在),μ=0.20(代表道路最大的横向力系数)。分别计算出对应的最大安全运行速度,如表 3(道路一般设计最小半径条件下)和表 4(道路极限设计最小半径下)所示。
| 设计速度/(km·h-1) | 一般最小半径/m | 超高 | 横向力系数对应的安全速度值/(km·h-1) | |||
| μ=0.07 | μ=0.10 | μ=0.15 | μ=0.20 | |||
| 120 | 1 000 | 0.06 | 95.38 | 105.82 | 121.23 | 134.89 |
| 100 | 700 | 0.06 | 79.80 | 88.53 | 101.43 | 112.86 |
| 80 | 400 | 0.07 | 62.60 | 68.98 | 78.48 | 86.94 |
| 60 | 200 | 0.08 | 45.82 | 50.19 | 56.74 | 62.60 |
| 40 | 100 | 0.07 | 31.30 | 34.49 | 39.24 | 43.47 |
| 30 | 65 | 0.06 | 24.32 | 26.98 | 30.91 | 34.39 |
| 20 | 30 | 0.06 | 16.52 | 18.33 | 21.00 | 23.36 |
| 设计速度/(km·h-1) | 极限最小半径/m | 超高 | 横向力系数对应的安全速度值/(km·h-1) | |||
| μ=0.07 | μ=0.10 | μ=0.15 | μ=0.20 | |||
| 120 | 650 | 0.08 | 82.60 | 90.49 | 102.29 | 112.86 |
| 100 | 400 | 0.08 | 64.80 | 70.98 | 80.24 | 88.53 |
| 80 | 250 | 0.08 | 51.23 | 56.12 | 63.44 | 70.00 |
| 60 | 125 | 0.08 | 36.22 | 39.68 | 44.86 | 49.49 |
| 40 | 60 | 0.08 | 25.10 | 27.49 | 31.08 | 34.29 |
| 30 | 30 | 0.08 | 17.75 | 19.44 | 21.97 | 24.25 |
| 20 | 15 | 0.08 | 12.55 | 13.75 | 15.54 | 17.14 |
将计算出的最大速度与道路设计速度进行比较,如图 4(道路一般设计最小半径条件下)和图 5所示(道路极限设计最小半径下)。
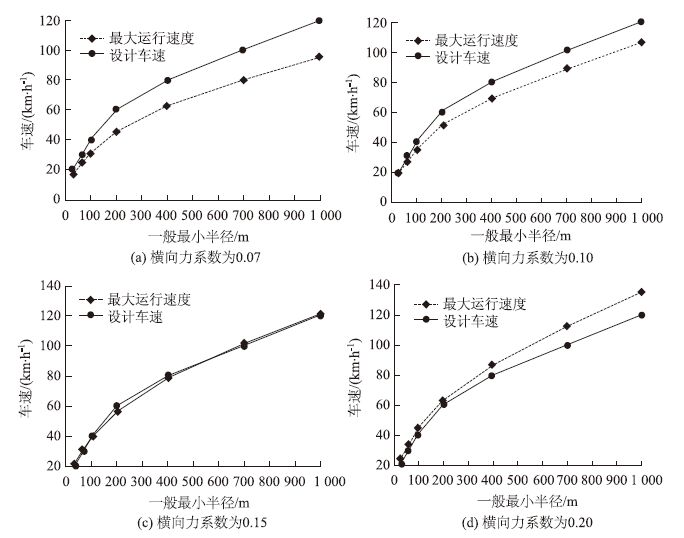 |
| 图 4 一般最小半径下最大安全运行速度 Fig. 4 Maximum safe driving speed in common minimum radius |
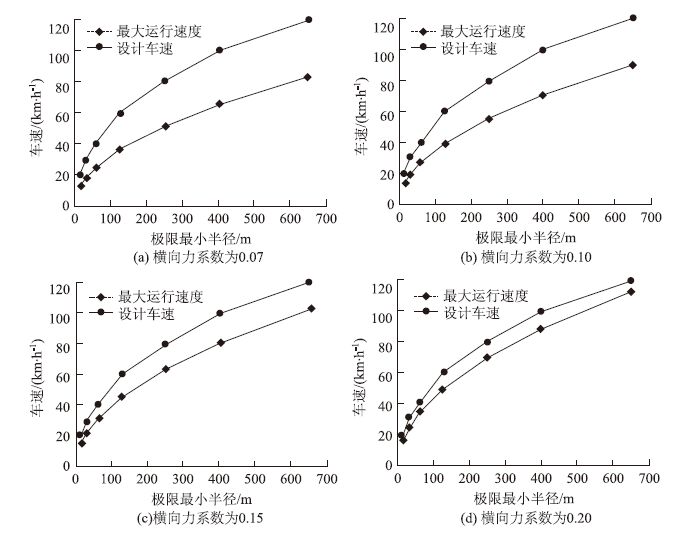 |
| 图 5 极限最小半径下的最大安全运行速度 Fig. 5 Maximum safe driving speed in limit minimum radius |
由表 3中的第7列可知,在一般最小半径下车辆还是会出现超速行为的,这可能导致交通事故的发生。由表 4的第7列可知,在极限最小半径下,车辆则不会出现超速,否则将出现横向不稳定。从图 4(a)和图 5(a)可以看出在积冰或积雪路面行驶时最大安全车速下降得较多,在平曲线设计采用极限半径条件下的时候速度下降尤为明显,这会导致交通流的不稳定性,易引起交通拥堵。
从整体上分析图 4和图 5发现:车辆在采用一般最小半径的平曲线上行驶时比在采用极限最小半径行驶时最大安全运行速度与设计车速的速差均较小,因此平曲线设计时优先选择一般最小半径。
4 结论论文首先对大型客车前后轴内外轮的受力进行了分析,确定了客车最易发生侧滑的车轮,并选取该车轮作为研究对象,综合考虑车辆结构、车辆动力学特性、道路平曲线与超高以及轮胎等因素。基于横向力系数建立了客车发生侧滑时的最大运行速度模型,并计算得到在不同路面条件和平曲线半径下的最大安全运行速度,并将其与道路的设计车速进行比较。计算结果表明,在一定的设计速度条件下,一般最小半径对应的最大安全运行速度比极限最小半径对应的最大安全运行速度更接近设计速度值,且在横向力系数较大时,一般最小半径对应的最大安全运行速度值比设计速度值大,确保了车辆行驶的安全性。同时,对于如挂车、大件运输车辆等常见的专用车辆,也可以利用该计算模型对其进行弯道行驶最大安全速度的计算,从而对这些车辆通过弯道的安全性做出评估。在道路设计与建设方面,研究结论可以为不同道路条件下的平曲线设计、安全核查、车速限制和驾驶员安全驾驶提供参考和建议。
| [1] | LIU Xing-wang.The Maximum Safe Speed Calculation Model Research on Curve [C]// First International Conference on Transportation Information and Safety (ICTIS), Reston: American Society of Civil Engineers, 2011:1642-1648. |
| [2] | 游克思, 武加恒, 孙璐, 等. 道路几何参数对车辆操纵稳定性影响[J]. 公路交通科技, 2011, 28(10): 109-117. YOU Ke-si, WU Jia-heng, SUN Lu, et al. Influence of Road Geometry Parameters on Vehicle Handling Stability[J]. Journal of Highway and Transportation Research and Development, 2011, 28(10): 109-117. |
| [3] | RAO S K. Unit Curve for Design of Highway Transition [J]. |
| [4] | 张金水, 张廷楷. 道路勘测与设计[M]. 上海:同济大学出版社, 2005. ZHANG Jin-shui, ZHANG Ting-kai. Road Survey and Design [M]. Shanghai: Tongji University Press, 2005. |
| [5] | JTGB 01—2003,公路工程技术标准[S]. JTGB 01—2003, Technical Standard of Highway Engineering [S]. |
| [6] | 杜瑞国, 王中元, 李振军. 车辆转弯不容忽略的力学问题[J]. 力学与实践, 2011, 33(4): 90-91. DU Rui-guo, WANG Zhong-yuan, LI Zhen-jun. Mechanical Problem of Vehicle Turning Cannot be Ignored [J]. Mechanics and Engineering, 2011, 33(4): 90-91. |
| [7] | 杨英. 大客车操纵稳定性动力学研究[D]. 吉林:吉林大学, 2002. YANG Ying. Research of Coach Steering Stability Dynamics [D]. Jilin: Jilin University, 2002. |
| [8] | MANFRED M, HENNING W, 陈荫三, 等. 汽车动力学[M]. 4版. 北京:清华大学出版社, 2009. MANFRED M, HENNING W, CHEN Yin-san, et al. Vehicle Dynamics [M].4th ed. Beijing: Tsinghua University Press, 2009. |
| [9] | 郭志勇, 王宏建. HQ6112A15型客车底盘悬架侧倾计算[J]. 机械工程师, 2007(2):110-111. GUO Zhi-yong, WANG Hong-jian. Calculation of Chassis Suspension Roll of HQ6112A15 Type Coach [J]. Mechanical Engineer, 2007(2):110-111. |
| [10] | 郭孔辉, 李宁, 庄晔. 轮胎侧向力影响因素试验[J]. 农业机械学报, 2011, 42(12):1-5. GUO Kong-hui, LI Ning, ZHUANG Ye. Affecting Factors Experiment in Tire Lateral Force [J]. Transactions of the Chinese Society for Agricultural Machinery, 2011, 42(12): 1-5. |
| [11] | 郭孔辉, 隋军. 轮胎垂直载荷分布与侧向力模型及纵向力之间的关系[J]. 汽车研究与开发, 1995(1):22-25. GUO Kong-hui, SUI Jun. Relationship of Tire Vertical Load Distribution with Lateral Force Model and Longitudinal Force [J]. Automotive Research and Development, 1995(1): 22-25. |
| [12] | GB 1589—2004, 道路车辆外廓尺寸、轴荷及质量限值[S]. GB 1589—2004, Limits of Dimensions,Axle Load and Masses for Road Vehicles [S]. |
| [13] | 王喜斌, 闫成柱. HQ6112A15型后置长途客车底盘与发动机的匹配设计计算[J]. 专用汽车, 1990(2):29-32. WANG Xi-bin, YAN Cheng-zhu. Matching Design and Calculation of HQ6112A15 Type Long Distance Rear Coach Chassis and Engine[J]. Special Purpose Vehicle, 1990(2): 29-32. |
| [14] | AWADALLAH F. Theoretical Analysis for Horizontal Curves Based on Actual Discomfort Speed [J]. |
| [15] | HILDEBRAND E D, LEWIS J. Driver Tolerance of Lateral Accelerations on Horizontal Curves [J]. |
 2016, Vol. 31
2016, Vol. 31
