公路交通科技  2016, Vol. 31 Issue (1): 130-134

扩展功能

文章信息

翁剑成, 葛昱, 王昌, 荣建, 闫卫坡
WENG Jian-cheng, GE Yu, WANG Chang, RONG Jian, YAN Wei-po
面向公交服务评价的公交出行指数与分析模型
Transit Travel Index and Analysis Models for Transit Service Evaluation
公路交通科技, 2016, Vol. 31 (1): 130-134
Journal of Highway and Transportation Research and Denelopment, 2016, Vol. 31 (1): 130-134
10.3969/j.issn.1002-0268.2016.01.020

文章历史

收稿日期: 2014-11-12
引用本文 0
翁剑成, 葛昱, 王昌, 荣建, 闫卫坡. 面向公交服务评价的公交出行指数与分析模型[J]. 公路交通科技, 2016, Vol. 31 (1): 130-134.
WENG Jian-cheng, GE Yu, WANG Chang, RONG Jian, YAN Wei-po. Transit Travel Index and Analysis Models for Transit Service Evaluation[J]. Journal of Highway and Transportation Research and Denelopment, 2016, Vol. 31 (1): 130-134.
面向公交服务评价的公交出行指数与分析模型
翁剑成1, 葛昱2, 王昌1, 荣建1, 闫卫坡3    
1. 北京工业大学 交通工程北京市重点实验室, 北京 100124;
2. 北京市交通委员会, 北京 100073;
3. 北京市首都公路发展集团有限公司, 北京 100073
收稿日期: 2014-11-12
基金项目: 国家科技重大专项项目(2013ZX01045003-002);北京市科委科技计划项目(D131100005113003).
作者简介: 翁剑成(1981-),男,浙江金华人,博士,副教授.
摘要: 从城市公共交通服务评价和出行者信息服务需求入手,通过多类别用户的指标筛选和优化流程,构建了涵盖公交出行便利性、快捷性、可靠性和舒适性4个维度的三级服务评价指标体系。并提出了基于公交站点N分钟覆盖率、平均运送速度、站点区间行程时间波动程度和断面满载率的公交出行指数分析模型。利用公交运行监测多源数据和基础参数,建立了城市公交便利指数、快捷指数、可靠指数和舒适指数的分析模型。以北京市公交GPS数据、IC卡数据为基础,验证了模型在服务评价、日常监测和运营管理等方面的适用性,分析结果表明:模型能为公交服务质量评价提供有效工具。
关键词: 交通工程     公交出行指数     指标体系     多源数据     公共交通     服务评价    
Transit Travel Index and Analysis Models for Transit Service Evaluation
WENG Jian-cheng1, GE Yu2, WANG Chang1, RONG Jian1, YAN Wei-po3     
1. Beijing Key Laboratory of Traffic Engineering, Beijing University of Technology, Beijing 100124, China;
2. Beijing Municipal Commission of Transport, Beijing 100073, China;
3. Beijing Capital Highway Development Group Co., Ltd., Beijing 100073, China
Abstract: Based on the requirements of urban transit service evaluation and traveler information service,through selecting multi-category users' indicators and optimization processes,we established a 3-level service evaluation index system covering 4 dimensions including convenience,rapidity,reliability and comfort. Then,we raised a transit travel index analysis model based on N-minute bus stop coverage,travel speed,volatility of travel time between bus stops,and section load ratio. Furthermore,using the multi-source data collected from the bus operation monitoring system and the basic parameters,we established the analysis models of convenience index (CI),rapid index (RI),reliability index (RBI) and comfortable index (CTI) for urban transit. Finally,by using the real bus GPS data and IC card data in Beijing,we verified the applicability of the models in service evaluation,daily monitoring and operation management and so on. The analysis result shows that the models can offer an effective tool for transit service quality evaluation.
Key words: traffic engineering     transit travel index     index system     multi-source data     transit     service evaluation    
0 引言

公共交通作为居民出行中服务受众最广，影响最大的交通出行方式，目前缺乏统一而有效的手段对其服务效率和服务质量进行准确评价。公交出行者不能准确获取公交出行畅通程度、舒适程度、可靠程度等相关的动态信息；公交运营管理者缺乏公交线路诊断和优化评价的有力手段；政府监管部门缺乏统一的公交出行效率评价指标。

国外关于公共交通评价指标的研究[1, 2, 3, 4]，主要集中在服务质量的影响因素与乘客满意度评价等方面，常用的指标有平均运送速度、准点率、公交站点覆盖率、发车间隔、到站间隔等。而国内的研究[5, 6, 7]主要侧重于建立概念指标体系，对服务水平的研究多为定性分析，评价指标系统基本涵盖了公共交通的各个方面，具体包括运行状况、服务水平、社会效益、经济效益等。

结合基于关注度的多类别出行者调查，基于重要度的多类别专家调查和基于数据质量的指标体系筛选等过程，本文从公共交通的便利性、快捷性、可靠性、舒适性等方面，选取了反映公交核心运行状况的关键指标，建立了一套公交出行指数体系。如表 1所示。

表 1 公共交通出行指数评价体系 Tab. 1 Transit travel index evaluation system
一级指标 二级指标 三级核心指标 数据基础
公交出行指数 公交便利指数 公交线路覆盖率 站点覆盖面积及人口数
公交快捷指数 公交运送速度 公交GPS数据、公交站点数据
公交可靠指数 公交线路行程时间波动 公交车辆在各站点间的行程时间
公交舒适指数 断面满载率 公交GPS数据、IC卡数据
表选项
1 公共交通出行指数分析模型 1.1 便利指数分析模型

公共交通便利指数(CI)反映乘客乘坐及换乘公交的方便程度。居民公交出行需要步行的距离越短，越便利。研究以全市或分区域的N分钟公交站点面积覆盖率及人口覆盖率为基础，计算公共交通便利指数。

(1)覆盖比例计算

在N分钟站点服务面积覆盖率(Area Coverage，AC)计算中，将站点覆盖的面积与所评价区域的总面积相比，确定N分钟公交站点面积覆盖率。计算公式如下：

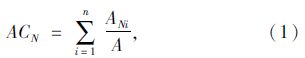
式中，ACN为N分钟公交站点面积覆盖率；n为评价区域内公交站点数；ANi为N分钟第i个公交站点的服务覆盖面积；A为区域总面积。

在N分钟站点人口覆盖率(Population Coverage，PC)计算中，统计站点覆盖区域内的人口数和所评价区域的总人口数，以此确定N分钟公交站点人口覆盖率。计算公式如下：

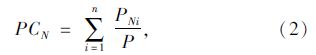
式中,PCN为N分钟公交站点人口覆盖率；PNi为N分钟第i个公交站点覆盖人口数；P为区域总人口数。

(2)公共交通便利指数

公共交通便利指数综合了站点面积覆盖率和站点人口覆盖率。指数越小，表明公共交通未覆盖区域和人口比例越小，便利程度越高。由于市区和郊区的站点面积覆盖率和人口覆盖率相差较明显，在此引入评价区域属性系数，用来表征不同区域的区位属性差异。公交便利指数计算公式如下：

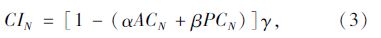
式中,CIN为公共交通便利指数；ACN为N分钟公交站点面积覆盖率；PCN为N分钟公交站点人口覆盖率；α,β分别为评价区域属性系数，作为区域面积覆盖率和区域人口覆盖率的综合权值，α+β=1.0；γ为便利指数归一化系数。

1.2 快捷指数分析模型

公共交通快捷指数(RI)反映公交服务的快捷程度，以站点区间的公交运送速度为基础，并考虑拥堵路段里程比例及拥堵时间比例对整个公交运行时空状况的影响[8]。快捷指数越高，表明公交线路的快捷性越差，运送旅客效率越低。

(1)公交运送速度计算

公交运送速度以相邻两个公交站点区间为最小单位，利用公交GPS数据及地理信息基础数据，可建立公交运送速度提取模型。根据不同道路等级，对公交运送速度进行等级划分，如表 2所示。

表 2 公交运送速度等级划分标准(单位：km/h) Tab. 2 Bus travel speed rating criterion(unit: km/h)
运行等级 1 2 3 4 5
高速路 V>60 50＜V≤60 40＜V≤50 25＜V≤40 V≤25
快速路 V>40 30＜V≤40 25＜V≤30 15＜V≤25 V≤15
主干路 V>35 25＜V≤35 20＜V≤25 12＜V≤20 V≤12
次干路、支路 V>30 22＜V≤30 16＜V≤22 10＜V≤16 V≤10
  注：V为公交运送速度。两个站点间的路径同时覆盖不同等级道路时，以占据的距离比例较大路段的道路等级为准。
表选项

(2)公交快捷指数计算模型

采用拥堵比例来反映公交运行快捷程度。线路拥堵比例PXk包括线路拥堵里程比例(即处于拥堵状态路段的里程占线路总里程的比值)和线路拥堵时间比例(即处于拥堵状态的路段所用的时间占整条线路运营时间的比值)。在判断线路运行状态过程中，认为站点区间速度等级为三级以上的路段均处于不同程度的拥堵状态。计算公式如下：

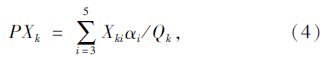
式中,PXk为拥堵比例，k取0或1,分别表示线路里程或线路行程时间；Q0为线路总里程；Q1为线路总行程时间；Xki为处于i等级的线路里程(k=0)或线路行程时间(k=1)；αi为模型权值系数，i取3,4,5时，αi为不同拥堵级别对快捷指数的影响系数。

公共交通线路快捷指数的取值范围为[0, 10]，计算公式如下：

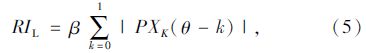
式中，RIL为线路快捷指数；θ为拥堵权重系数，取值范围为[0, 1]；β为快捷指数归一化系数。

公共交通线网快捷指数可以综合刻画公交线网运行的快捷程度。以线路快捷指数为基础，利用人车公里数作为线路的权重值，将所有的线路快捷指数加权计算得到线网快捷指数。客运量越大、行程越长的线路对线网快捷指数的贡献率将越大。

1.3 可靠指数分析模型

公共交通可靠指数(RBI)表征了乘客在分析时间段内能够按照既定时间到达目的地的可靠程度。站点区间的公共交通车辆行程时间的波动程度越大，表明车辆到达站点的时间间隔分布越不均匀，准点程度越低。

(1)公交站点区间可靠度指数

假设Tij为车辆从站点i到j的实际行程时间，T-ij为一周内所有车次行程时间的均值。根据模型测试，训练确定E作为可靠度评估阈值参数，若车辆在站点i，j之间的行程时间在均值的E％范围内，则认为行程区间运行可靠。计算一周内站点间行程时间Tij落在均值E%区间以外的概率，表示行程时间波动较大的样本占总体样本的比例。即：

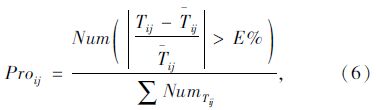
式中，Proij为站点间行程时间大偏差比例；T-ij为一周内所有车次行程时间均值。

此外，同时考虑全体样本偏差的分布特性对公共交通可靠指数的影响，研究引入站点区间行程时间的离散系数(Coefficient of Dispersion，CD)，对行程时间波动大于E%的比例进行折减。离散系数的计算公式如下：

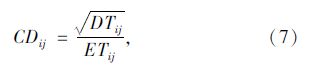
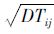式中，CDij为离散系数；为站点i到站点j之间的行程时间标准差；ETij为站点i到站点j之间的行程时间均值。

结合分级比例计算值与定量折减，得到公共交通站点区间可靠指数。公共交通可靠指数的值阈为[0, 10]，计算公式如下：

式中，RBIij为公共交通站点区间可靠指数；α为模型比例系数。

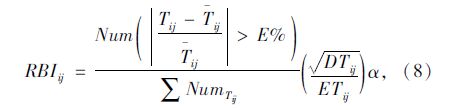
(2)公交线路的可靠度指数

公交线路可靠指数刻画整条线路的运行可靠程度。线路各站点区间的可靠度指数同样以人车公里数为基础，计算站点的权重值加权求和得到线路可靠度指数。

1.4 舒适指数分析模型

公共交通舒适度指数(CTI)反映了乘客乘坐公交的舒适程度，用满载率指标来表征。满载率越高，表明车厢内越拥挤，乘坐舒适度越差。

(1)断面满载率

断面满载率指两个站点间行驶车辆的断面客流量(Passenger Flow Volume，PFV)与该站点区间断面额定载客量(Rated Capacity，RC)的比值。其中，车辆通过站点区间断面的客位数根据经过该断面的车辆数计算，站点区间的断面客流量则需要对公交IC卡刷卡数据分析，利用站点聚类分析[9]和客流提取模型，匹配站点区间客流量。公共交通断面满载率的计算公式为：

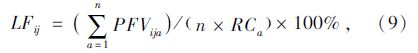
式中，LFij为站点i与站点j之间的断面满载率；PFVija为车辆a在站点区间i，j的断面客流量；RCa为车辆a的车辆额定载客量；n为单位时间内经过站点区间[i,j]的车辆数。

(2)公交线路舒适度指数

基于满载率数值建立公交舒适度指数计算模型，包含站点区间舒适度和线路舒适度指数。站点区间的舒适度指数的计算公式如下：

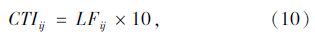
式中，CTIij为站点i到站点j之间的站点区间舒适指数；LFij为站点i与站点j之间的断面满载率。

1.5 公共交通出行指数分级

为了便于评价公交服务水平，对各类公交出行指数进行了等级划分，如表 4所示。在应用中可直接利用分项指数进行专门评价，也可根据不同类别用户的需求和分项指标的偏好，确定合理的分项指标权值，综合加权得到综合评价等级。分项出行指数等级和综合评价指数等级处于四级和五级时，则认为公交运行质量或服务水平较差。

表 4 公共交通出行指数等级划分 Tab. 4 Rating of transit travel indexes
评价等级 出行指数类别
便利指数 快捷指数 可靠指数 舒适指数
一级 [0,2) ［0,2) ［0,2) ［0,3)
二级 ［2,4) ［2,4) ［2,4) ［3,4)
三级 ［4,6) ［4,6) ［4,6) ［4,7)
四级 ［6,8) ［6,8) ［6,8) ［7,9)
五级 ［8,10] ［8,10] ［8,10] [9,+∞)
  注：一级为非常好；二级为好；三级为一般；四级为差；五级为非常差。
表选项
2 公共交通出行指数模型应用

随着公共交通智能化采集手段的逐步完善，在公交GPS数据和IC卡刷卡交易数据的公交运送速度计算模型、公交断面客流提取模型的基础上，利用前文构建的公交出行指数分析模型，能实现公交运行状态的连续监测和评价。

(1)公共交通便利指数

便利指数可以按照分析需求确定分析区域。以北京市五环内作为分析对象，以各个区域的5 min站点覆盖面积率、覆盖人口率及便利指数进行说明，如表 5所示。

表 5 不同区域5分钟公交站点覆盖率及便利指数 Tab. 5 Five-minute bus stop coverages and CIs of different regions
站点覆盖率 二环内 二环与三环之间 三环与四环之间 四环与五环之间
5 min面积覆盖率/% 84.6 85 78.0 48.3
5 min人口覆盖率/% 87.6 87.1 81.8 57.5
CI5 1.39 1.40 2.01 4.71
表选项

从分析结果可知，四环以内的公交便利指数比四环与五环之间区域高，表明城市核心区出行较为便利，而四环与五环之间区域的公交站点覆盖水平尚有一定的提升空间。

(2)公共交通快捷指数

以北京市实时获取的公交GPS数据为基础，计算公交线网分时段的快捷指数，日变曲线如图 1所示。可以看出，公交线网快捷指数受高峰时段影响较为明显，早晚高峰期间与平峰期间的差异较大，高峰期间公交运行处于一般状态，快捷性受到一定影响。

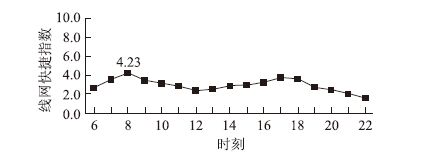图 1 公交线网的分时段快捷指数曲线(2012-05-29) Fig. 1 Hourly RI curve of transit network (2012-05-29)
图选项

线路快捷指数也能刻画不同线路运行的快捷程度差异，研究选取了707路(主干路)、658路(快速路)和13路(次干路和支路)3条公交线路为例说明，如图 2所示。

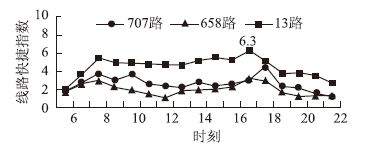图 2 不同线路分时段快捷指数曲线(2012-05-29) Fig. 2 Hourly RI curves of different bus lines(2012-05-29)
图选项

结果表明，13路的快捷指数明显高于其他两条线路，整体运行状态最差。从空间角度分析也表明，不同等级道路上的公交线路，其快捷指数的高低呈现较为明显的规律：次干路和支路>主干路>快速路。

(3)公共交通可靠指数

不同公交线路由于路线走向的差异，其可靠指数有明显的差异。计算300路内环(快速路)、52路(主干路)、1路(次干路)、8路(支路)等几条公交线路的分时段可靠指数，如图 3所示。

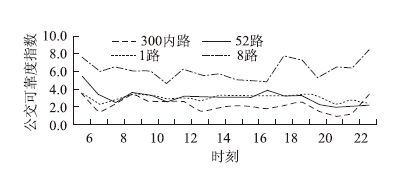图 3 不同公交线路可靠指数曲线 Fig. 3 RBI curves of different bus lines
图选项

从时间分布上看，清晨和夜间时段，受车辆自身状况及驾驶员习惯的影响较大；早晚高峰时段，道路运行状况差，车辆行程时间变化较大，可靠指数较大。

从道路等级分布上看，运行在快速路上的300路内环可靠指数小，可靠度较高，运行在支路的8路可靠度最低。表明线路所在的道路等级越高，公交行程时间的可靠度越高，线路可靠指数值越小。

(4)公交舒适指数

以公交486路(四方桥西—豆各庄路口南)在早高峰8：00—9：00时段的IC卡刷卡数据为基础，计算各站点间的公交舒适指数，如图 4所示。

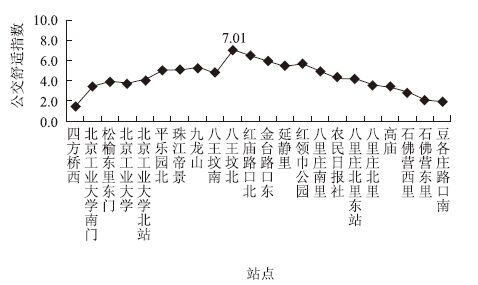图 4 486路公交线路站点舒适指数曲线 Fig. 4 CTI curves of bus line 486
图选项

可以看出，因换乘地铁而下车乘客居多的站点(八王坟南站)，舒适指数有所下降，而由地铁换乘而上车乘客人居多的站点(八王坟北站)，舒适指数又明显回升，达到最大值7.0，属于不舒适的等级。

3 结论

本文从公共交通出行便利性、快捷性、可靠性和舒适性等方面，通过多类别用户的指标筛选流程，构建了公共交通出行指标评价体系。基于多源公交数据，结合指标体系中的关键指标，建立了公交便利指数、快捷指数、可靠指数和舒适指数的测算和分析模型。利用北京市公交实际运行数据，验证了出行指数模型在城市公交评价和监测中的适用性，表明公交出行指数能较为客观和准确地反映公共交通的出行服务水平和特征。在此基础上建立了公共交通日常运行监测及服务评价系统。

参考文献
[1] XIE L, NAUMANN M, SUHL L. A Stochastic Model for Rota Scheduling in Public Bus Transport[R]. Paderborn, Germany: University of Paderborn, 2012.
[2] 徐群岭. 基于免疫优化的公交驾驶员调度问题[J].计算机工程,2010,36(24):164-166. XU Qun-ling. Schedule Problem of City Bus Drivers Based on Immune Optimization[J]. Computer Engineering,2010,36(24):164-166.
[3] LOURENÇO H R, PORTUGAL R. Multiobjective Metaheuristics for the Bus Driver Scheduling Problem[J].
[4] CEDER A.公共交通规划与运营:理论、建模及应用[M].北京:清华大学出版社,2010. CEDER A. Public Transit Planning and Operation: Theory, Modeling and Practice[M]. Beijing: Tsinghua University Press, 2010.
[5] 毛霖,李文权.公交线路车辆排班模型及算法研究[J].交通运输工程与信息学报,2009,7(3):64-67. MAO Lin, LI Wen-quan. Research on Transit Vehicle Scheduling Model and Its Algorithm [J].Journal of Transportation Engineering and Information, 2009,7(3):64-67.
[6] MESQUITA M, MOZ M, PAIAS A, et al. A Decomposition Approach for the Integrated Vehicle-crew-roster Problem with Days-off Pattern[J].
[7] LIN X, KLIEWER N, SUHL L. Integrated Driver Rostering Problem in Public Bus Transit[J].
[8] MESQUITA M, MOZ M, PAIAS A, et al. A New Model for the Integrated Vehicle-crew-rostering Problem and a Computational Study on Rosters[J].
[9] RESPÍCIOA, MOZ M, PATO M V. Enhanced Genetic Algorithms for a Bi-objective Bus Driver Rostering Problem: A Computational Study[J].
[10] 杨英俊,王轶萍,赵祥模.基于遗传算法的城市客运出租汽车调度中心人员排班研究[J].公路交通科技,2010,27(7):142-146. YANG Ying-jun, WANG Yi-ping, ZHAO Xiang-mo. Research on Staff Scheduling of Urban Passenger Taxi Dispatching Center Based on Genetic Algorithm[J]. Journal of Highway and Transportation Research and Development, 2010,27(7):142-146.
[11] 杨尚.基于蚂蚁算法的公交驾驶员调度问题研究[D].武汉:华中科技大学,2009. YANG Shang. Study on Bus Driver Scheduling Problem Based on Ant Algorithm[D]. Wuhan: Huazhong University of Science and Technology,2009.
[12] 翟东伟. 基于GATS的公交驾驶员调度算法研究[D].北京:北京交通大学,2007. ZHAI Dong-wei. Study on Bus Driver Scheduling Algorithm Based on GATS[D]. Beijing: Beijing Jiaotong University,2007.
[13] 王健.公交司售人员排班集合覆盖问题的求解算法研究与实现[D].北京:北京交通大学,2011. WANG Jian. Research and Implementation of Bus Crew-scheduling Algorithm Based on Set-covering Problem[D]. Beijing: Beijing Jiaotong University, 2011.