扩展功能
文章信息
- 魏金丽, 郭亚娟, 张萌萌
- WEI Jin-li, GUO Ya-juan, ZHANG Meng-meng
- 基于集合覆盖理论的公交线路驾驶员排班优化方法
- A Method of Optimizing Work Schedule of Bus Drivers Based on Set Covering Theory
- 公路交通科技, 2016, Vol. 31 (1): 125-129
- Journal of Highway and Transportation Research and Denelopment, 2016, Vol. 31 (1): 125-129
- 10.3969/j.issn.1002-0268.2016.01.019
-
文章历史
- 收稿日期: 2014-09-22
2. 吉林大学 交通学院, 吉林 长春 130022;
3. 山东交通学院 交通与物流工程学院, 山东 济南 250023
2. School of Traffic, Jilin University, Changchun Jilin 130022, China;
3. School of Traffic and Logistics Engineering, Shandong Jiaotong University, Jinan Shandong 250023, China
随着城市交通拥堵问题的日益严重,城市公共交通的主体地位也逐渐凸显。目前,为了进一步提升公交服务水平,政府投入了大量资金建设智能公共交通系统。其中,行车计划编制和公交线路驾驶员排班优化是公交系统实现智能调度的重要组成部分,直接影响到公交运营效率。
国外有关公交驾驶员排班问题的理论研究与实践探索已有50多年的历史[1, 2, 3];而国内的相关研究工作最近几年才逐渐开展,已取得一定研究成果[4, 5]。总体来看,国内外的研究主要可以分为两大主流:(1)驾驶员与公交车的集中调度[6, 7, 8];(2)将驾驶员调度当成一个孤立的问题看待。前者有利于降低公交运营的总成本,后者方便公交企业的灵活运营。独立的公交线路驾驶员排班模型算法主要集中于遗传算法[9, 10]、蚂蚁算法[11]、禁忌算法[12]和分支定界法[13]等。但这些算法都比较繁杂,不利于实现。
从公交公司运营管理角度出发,在公交运营车辆最少的前提下,公交驾驶员的成本最小即可满足公交公司利益最大化。因此本文以公交驾驶员成本最小为目标,将公交驾驶员排班问题抽象为一个集合覆盖问题,并设计启发式方法与0-1整数规划相结合的算法,最后采用MATLAB实现问题的求解。
1 公交线路驾驶员排班问题的分析公交线路驾驶员排班是根据编制的行车作业计划安排驾驶员的工作。在安排驾驶员工作时应该同时满足以下条件:(1)驾驶员每天的工作一般是由一辆车或两辆车的几段工作组成的;(2)运营的公交车辆所有的工作必须包含到驾驶员的工作中,所有驾驶员的工作集合必须覆盖运营车辆的任务。由此可以看出,公交线路驾驶员排班是一个极其复杂的组合优化问题。
在公交实际运营中,驾驶员排班首先将车辆的运营工作按照换班时间点划分成一个小驾驶段集合,然后在满足一系列目标和约束的基础上将这个小驾驶段集合重新整合、连接形成一个连续驾驶段集合,最后将几个连续驾驶段连接并将其分配给一个公交驾驶员完成,即形成一个班次。可以看出,公交驾驶员排班本质上是一个组合优化问题,而这个组合优化问题是很复杂的,其复杂性主要表现在目标多、规模大、约束条件复杂多样。
为消除公交驾驶员排班问题的复杂性,文献[13]中提出了一种列生成算法来解决集合覆盖问题,其难点在于求解初始可行解。在构建初始可行解时利用的贪婪算法和驾驶段配对方法较为复杂,初始排班方案会直接影响受限主问题的求解规模以及整个算法的循环迭代次数。本文在其基础上,设计了一种较为简单便捷的启发式算法得到可行班次集合,增加了算法的适用性。
2 公交线路驾驶员排班模型 2.1 模型原理公交线路驾驶员排班是一个将连续驾驶段予以集合,并在满足一系列目标和约束条件的基础上重新整合、连接的过程。首先将车辆调度所得的车次链按换班点分割成若干小驾驶段,考虑劳动法规约束,把小驾驶段合并成一些可行的连续驾驶段,然后对连续驾驶段进行任意组合筛选得出可行的班次集合,最后基于公交驾驶员成本最小化对可行的班次集合进行选择和再优化,即得到最终的劳动班次。
2.2 算法设计本文结合启发式方法和0-1整数规划,设计了解决公交线路驾驶员排班问题相应的算法。该算法可分为4个模块:连续驾驶段确定模块、可行班次集合产生模块、班次选择模块和班次优化模块。
(1)连续驾驶段确定模块
确定每个连续驾驶段即确定驾驶员每个工作时间段的长短。该模块为了保证驾驶员劳动法则的约束,采用有效工时不超过8 h来实现。为了保证驾驶员在连续驾驶段内较高的工作效率,采用小驾驶段之间的最小时间间隔来约束。具体的模块算法如下。
该模块已知每条车次链中每个小驾驶段的起始时间和起始地点。其中定义第p个车次链(班次)中第k个小驾驶段的起始时间为tpks和结束时间为tpke,第p个车次链中第k个小驾驶段的起始地点为zpks和结束地点为zpke。
求解每条车次链分割成的连续驾驶段的起始时间、起始地点以及所在车次链编号。
该模块的约束条件有两个。
① 每条车次链中任意相邻的两个小驾驶段之间的空闲时间不得大于0.5 h,即:
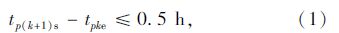
② 由每条车次链中a个连续小驾驶段合并得到的连续驾驶段有效工时不得大于8 h,即:
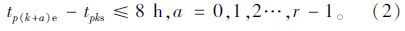
(2)可行班次集合产生模块
在实际运营中,一个公交线路驾驶员排班问题的规模是由连续驾驶段个数或者换班点个数所决定的。为了解决驾驶员实际换班时换车困难的问题,该模块对上一个模块所获得的连续驾驶段任意组合后,利用启发式方法筛选掉部分换班点来缩小问题规模,通过限制最小换车次数、确保组合中任意两个相邻连续驾驶段之间换班时间协调且换班地点一致,从而产生可行班次集合S。具体的模块算法如下。
已知连续驾驶段集合中元素对应的起始时间Tpks、结束时间Tpke、起始地点Zpks、结束地点 Tpke以及所属的车次链编号。
利用以上数据求出可行的班次集合S,即连续驾驶段的可行组合。同时求出班次选择模块中目标函数需用的数据αij与Tzbj(αij与Tzbj具体释义见式(7)后)。
其中约束条件如下。
①每个班次j覆盖的连续驾驶段个数最多为4,即1≤N≤4。
②每个班次j覆盖的连续驾驶段最多跨越两个车次链,且必须满足每个班次只能从一个车次链到另一个车次链跨越1次。
③连续驾驶段换班时间的限制,即每个班次j中相邻的两个连续驾驶段必须满足:前一个连续驾驶段i的结束时间必须早于下一个连续驾驶段i+1的起始时间,满足:

④ 连续驾驶段换班地点的限制,即在一个班次j中,相连接的两个连续驾驶的结束与起始时间间隔小于Tsingle时,前一个连续驾驶段i的结束地点是后一个连续驾驶段i+1的起始地点,即满足:
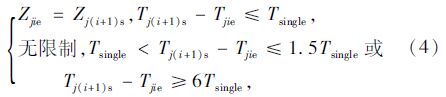
(3)班次选择模块
为了保证人员排班的合理性和公平性,单个班次的运营成本计算应该是有效工时成本与超过劳动法则规定工作时间T的加班工资成本之和。在此基础上,基于集合覆盖思想进行建模。通过求解该模块中0-1整数规划问题,从可行班次集合S中选出基于人员成本最小化的可行班次集合Q,使集合Q中的全部元素结合起来能够覆盖全部的车辆运营工作。
此0-1整数规划问题具体为:
①所求的变量
xj=1,若班次j被选中0,否则,(5)
式中xj表示班次j是否被选中,j=1,2,…,n。
② 目标函数

式中cj为班次j的人员成本。
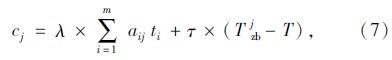
式中, ;ti为连续驾驶段i的有效工时;λ为班次j的人员成本系数,班次分别覆盖1,2,3,4个连续驾驶段时,λ分别为1,0.9,0.8,0.7(班次覆盖连续驾驶段个数较多的,人员成本系数低,利于优先选择);τ为加班权重系数,
;ti为连续驾驶段i的有效工时;λ为班次j的人员成本系数,班次分别覆盖1,2,3,4个连续驾驶段时,λ分别为1,0.9,0.8,0.7(班次覆盖连续驾驶段个数较多的,人员成本系数低,利于优先选择);τ为加班权重系数, ;Tzbj为班次j的工作时间;T为劳动法则规定的工作时间,一般取8 h。
;Tzbj为班次j的工作时间;T为劳动法则规定的工作时间,一般取8 h。
③ 约束条件
每个连续驾驶段都会被唯一的班次覆盖,即保证:

(4)班次优化模块
该模块利用启发式方法进一步筛选掉已生成的但不太“好”的班次,即对以上所得的基于人员成本最小化的可行班次集合Q,进行班次的最后优化,得到最终的班次集合O。
其中进行优化的约束条件为:
可行班次集合Q中在班时间小于5 h的班次为需要优化的班次,而需要优化的班次中任意两个班次c与d之间的空闲时间大于等于5 h可合并优化为一个新的班次,即满足:
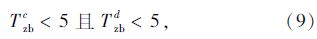
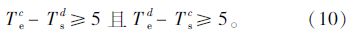
该模型具体的优化流程如图 1所示。
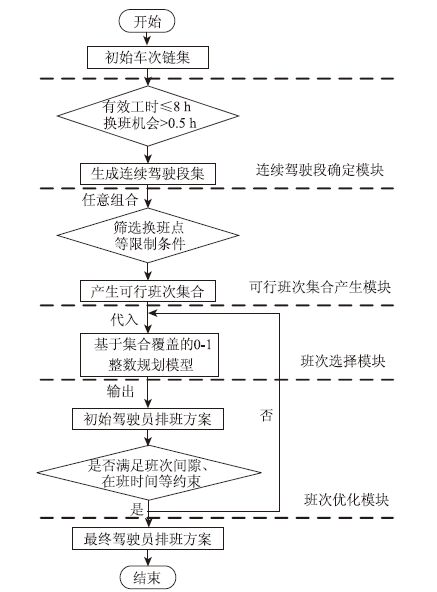 |
| 图 1 基于集合覆盖理论的公交线路驾驶员排班优化流程图 Fig. 1 Flowchart of optimizing work schedule of bus drivers based on set covering theory |
根据济南市某公交线路的行车作业计划表,以公交线路的换班点为分界,将该公交线路的3条车次链划分成若干小驾驶段,得到小驾驶段的到发时刻表,如表 1所示。
| 小驾驶段编号 | tpks | tpke | zpks | zpke | 车辆编号 |
| 1 | 5:30 | 6:30 | 1 | 2 | 1 |
| 2 | 6:50 | 7:50 | 2 | 1 | 1 |
| 3 | 8:00 | 9:00 | 1 | 2 | 1 |
| 4 | 9:20 | 10:25 | 2 | 1 | 1 |
| 5 | 10:35 | 11:35 | 1 | 2 | 1 |
| 6 | 12:05 | 13:05 | 2 | 1 | 1 |
| 7 | 13:10 | 14:10 | 1 | 2 | 1 |
| 8 | 16:40 | 17:40 | 2 | 1 | 1 |
| 9 | 18:10 | 19:10 | 1 | 2 | 1 |
| 10 | 19:40 | 20:30 | 2 | 1 | 1 |
| 11 | 20:45 | 21:50 | 1 | 2 | 1 |
| 12 | 7:30 | 8:30 | 2 | 1 | 2 |
| 13 | 9:00 | 10:00 | 1 | 2 | 2 |
| 14 | 10:20 | 11:20 | 2 | 1 | 2 |
| 15 | 11:25 | 12:30 | 1 | 2 | 2 |
| 16 | 13:45 | 14:40 | 2 | 1 | 2 |
| 17 | 14:50 | 15:40 | 1 | 2 | 2 |
| 18 | 15:45 | 16:50 | 2 | 1 | 2 |
| 19 | 20:00 | 21:00 | 1 | 2 | 2 |
| 20 | 21:10 | 22:10 | 2 | 1 | 2 |
| 21 | 8:30 | 9:30 | 1 | 2 | 3 |
| 22 | 9:40 | 10:10 | 2 | 1 | 3 |
| 23 | 10:15 | 11:15 | 1 | 2 | 3 |
| 24 | 12:45 | 13:45 | 2 | 1 | 3 |
| 25 | 14:00 | 14:50 | 1 | 2 | 3 |
| 26 | 14:50 | 15:45 | 2 | 1 | 3 |
| 27 | 17:00 | 18:10 | 1 | 2 | 3 |
| 28 | 18:30 | 19:30 | 2 | 1 | 3 |
| 29 | 20:00 | 21:05 | 1 | 2 | 3 |
| 30 | 21:15 | 22:15 | 2 | 1 | 3 |
利用上述算法步骤,编制相应的MATLAB程序实现该问题的求解。其过程中可得到连续驾驶段的到发时刻表,如表 2所示。
| 连续驾驶段编号 | 覆盖的小驾驶段 | 所属车次链 | Tpks | Tpke | Zpks | Zpke |
| 1 | 1,2,3,4,5,6 | 1 | 5:30 | 13.05 | 1 | 1 |
| 2 | 7 | 1 | 13:10 | 14:10 | 1 | 2 |
| 3 | 8,9,10,11 | 1 | 16:40 | 21:50 | 2 | 2 |
| 4 | 12,13,14,15 | 2 | 7:30 | 12:30 | 2 | 2 |
| 5 | 16,17,18 | 2 | 13:45 | 16:50 | 2 | 1 |
| 6 | 19,20 | 2 | 20:00 | 22:10 | 1 | 1 |
| 7 | 21,22,23 | 3 | 8:30 | 11:15 | 1 | 2 |
| 8 | 24,25,26 | 3 | 12:45 | 15:45 | 2 | 1 |
| 9 | 27,28,29,30 | 3 | 17:00 | 22:15 | 1 | 1 |
将以上所得的连续驾驶段代入模型求解,并进行再次优化,得最终班次表,如表 3所示。
从计算结果可以看出,该方法体现了两个方面的优点:(1)能够有效提高驾驶员的工作效率,减少候车时间消耗,例如班次1、班次3、班次4;(2)如果驾驶员在一天内需要分时段行驶,则需要为其在换班点留够足够的休息时间,例如班次2、班次5。
为了验证本文算法的性能,选取实际人工编制和遗传算法[9]得出其他两种不同的排班方案,以此进行对比分析。各个调度方案的相关性能数据分析如表 4所示。可以看出,本文算法的班次个数最少,且相应的班次总工作时间和人员成本也都最小,同时能够保证较快的优化速度,即MATLAB优化实现时间。因此可验证本文算法得出的排班方案最优,既能有效减少人员成本支出,又能提高排班速度。
| 算法 | 班次个数 | 班次总工作时间/min | 人员成本/CNY yuan | 优化时间/min |
| 本文算法 | 5 | 2 050 | 1 171.45 | 1.5 |
| 人工编制 | 6 | 2 445 | 1 200.67 | 5 |
| 遗传算法 | 7 | 2 350 | 1 184.21 | 3 |
在分析公交驾驶员排班问题复杂性的基础上,以人员总成本最小化为目标,考虑公交驾驶员排班问题的车辆运营任务、换班时间、劳动规则要求等约束,借助集合覆盖问题进行数学建模,并融合启发式方法和0-1整数规划设计算法进行了模型的求解。最后,结合济南市公交公司的实际数据,以MATLAB为平台,实现了以上算法,求出了公交驾驶员排班方案。该方案很好地解决了提高驾驶员工作连续性的问题。
本文研究的重点是单条公交线路的排班问题,只能满足对单条线路的求解要求,但相对于大规模的多场站跨线路的驾驶员排班问题,这种模型和算法仍有待改进。
| [1] | XIE L, NAUMANN M, SUHL L. A Stochastic Model for Rota Scheduling in Public Bus Transport[R]. Paderborn, Germany: University of Paderborn, 2012. |
| [2] | 徐群岭. 基于免疫优化的公交驾驶员调度问题[J].计算机工程,2010,36(24):164-166. XU Qun-ling. Schedule Problem of City Bus Drivers Based on Immune Optimization[J]. Computer Engineering,2010,36(24):164-166. |
| [3] | LOURENÇO H R, PORTUGAL R. Multiobjective Metaheuristics for the Bus Driver Scheduling Problem[J]. |
| [4] | CEDER A.公共交通规划与运营:理论、建模及应用[M].北京:清华大学出版社,2010. CEDER A. Public Transit Planning and Operation: Theory, Modeling and Practice[M]. Beijing: Tsinghua University Press, 2010. |
| [5] | 毛霖,李文权.公交线路车辆排班模型及算法研究[J].交通运输工程与信息学报,2009,7(3):64-67. MAO Lin, LI Wen-quan. Research on Transit Vehicle Scheduling Model and Its Algorithm [J].Journal of Transportation Engineering and Information, 2009,7(3):64-67. |
| [6] | MESQUITA M, MOZ M, PAIAS A, et al. A Decomposition Approach for the Integrated Vehicle-crew-roster Problem with Days-off Pattern[J]. |
| [7] | LIN X, KLIEWER N, SUHL L. Integrated Driver Rostering Problem in Public Bus Transit[J]. |
| [8] | MESQUITA M, MOZ M, PAIAS A, et al. A New Model for the Integrated Vehicle-crew-rostering Problem and a Computational Study on Rosters[J]. |
| [9] | RESPÍCIOA, MOZ M, PATO M V. Enhanced Genetic Algorithms for a Bi-objective Bus Driver Rostering Problem: A Computational Study[J]. |
| [10] | 杨英俊,王轶萍,赵祥模.基于遗传算法的城市客运出租汽车调度中心人员排班研究[J].公路交通科技,2010,27(7):142-146. YANG Ying-jun, WANG Yi-ping, ZHAO Xiang-mo. Research on Staff Scheduling of Urban Passenger Taxi Dispatching Center Based on Genetic Algorithm[J]. Journal of Highway and Transportation Research and Development, 2010,27(7):142-146. |
| [11] | 杨尚.基于蚂蚁算法的公交驾驶员调度问题研究[D].武汉:华中科技大学,2009. YANG Shang. Study on Bus Driver Scheduling Problem Based on Ant Algorithm[D]. Wuhan: Huazhong University of Science and Technology,2009. |
| [12] | 翟东伟. 基于GATS的公交驾驶员调度算法研究[D].北京:北京交通大学,2007. ZHAI Dong-wei. Study on Bus Driver Scheduling Algorithm Based on GATS[D]. Beijing: Beijing Jiaotong University,2007. |
| [13] | 王健.公交司售人员排班集合覆盖问题的求解算法研究与实现[D].北京:北京交通大学,2011. WANG Jian. Research and Implementation of Bus Crew-scheduling Algorithm Based on Set-covering Problem[D]. Beijing: Beijing Jiaotong University, 2011. |
 2016, Vol. 31
2016, Vol. 31
