扩展功能
文章信息
- 林贵宝, 马荣国, 杨泞珲
- LIN Gui-bao, MA Rong-guo, YANG Ning-hui
- 机非划线分割道路自行车交通流对机动车运行的影响
- Impact of Bicycle Traffic on Vehicle Operation on Divided Road
- 公路交通科技, 2016, Vol. 31 (1): 112-118
- Journal of Highway and Transportation Research and Denelopment, 2016, Vol. 31 (1): 112-118
- 10.3969/j.issn.1002-0268.2016.01.017
-
文章历史
- 收稿日期: 2014-12-14
2. 南京理工大学 自动化学院, 江苏 南京 210094
2. School of Automation, Nanjing University of Science and Technology, Nanjing Jiangsu, 210094, China
在过去的十多年中,世界上许多国家自行车的使用量迅速增加[1, 2, 3]。在一些自行车使用量较大的国家,例如我国,将城市道路中的自行车道设置得相当宽(如3~5 m),以此来满足自行车交通的大流量以及减少对机动车运行的干扰。随着自行车交通流量的增加,自行车道不再满足自行车的出行需求而借助机动车道。在这种情况下,自行车交通将会给机动车运行带来一些干扰。由于市区机动车停车需求的增加,交通部门考虑通过减小自行车道宽度而设置路内停车,但这种措施会加剧自行车与机动车之间的冲突,机动车运行的延误也会随之大大增加。
国内外大多数研究侧重于分析市区内自行车与机动车在交叉口的相互影响[4, 5, 6]。陈景旭等[5]建立了一套模型来评价左转自行车交通在信号交叉口对机动车的影响,然而这种模型并不能直接用于道路断面的分析。其他研究者分析了机非划线分割道路的交通运行状况以及服务水平[7, 8, 9, 10, 11, 12]。贾顺平等[9]定量分析了自行车对机动车的摩擦干扰和阻滞干扰。但这些研究尚未解决一个关键问题,即自行车在不同流量情况下对机动车造成的延误影响。
本文主要通过南京市的调查数据,分析不同交通状况下自行车交通流的特征以及机动车的速度,建立模型预测自行车交通在城市道路内对机动车造成的延误,研究自行车交通在划线分割道路上对机动车运行的影响。
1 数据调查选取进行数据采集的城市道路必须满足以下要求:(1)自行车-机动车划线分割道路;(2)行人对机动车道和自行车道无干扰或干扰较小;(3)所选道路断面应远离交叉口的上游或下游;(4)道路内没有公交停靠站;(5)在视野开阔的观察点以及较高的位置架设摄像机(在高层建筑或人行天桥上等);(6)自行车和机动车交通流量大,能够反映大多数交通状况。最后,在南京选取6条典型的城市道路进行数据采集。
选取地点信息如表 1所示。自行车道宽度从0.5 m 到2.1 m,机动车道数从1车道到2车道,其中有3条道路的自行车道右边设置了路内停车。在2014年5月的3个工作日(天气良好)内采集数据,为了得到非机动车与机动车的各种交通状况,时间段包括非高峰期和高峰期。摄像机架设在调查的道路断面附近,以便能够拍摄全程的交通状况,如图 1所示。
| 编号 | 道路名称 | 机动车道数 | 自行车道宽度/m | 路内停车 |
| 1 | 建国路 | 1 | 0.5 | 是 |
| 2 | 文艺南路 | 2 | 0.5 | 是 |
| 3 | 建设路 | 1 | 1.0 | 否 |
| 4 | 大学南路 | 1 | 1.0 | 是 |
| 5 | 南新街 | 2 | 1.3 | 否 |
| 6 | 青龙路 | 2 | 2.1 | 否 |
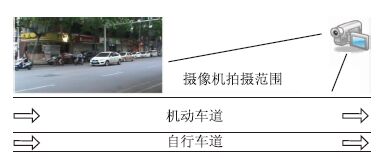 |
| 图 1 摄像机数据采集 Fig. 1 Data acquisition by camera |
本文运用累计曲线法从视频数据中获取机动车与自行车的交通流信息。累计曲线法是检验两个参数间关系一致性及其变化的常用方法,通常是一条 平滑的S形曲线。运用累计曲线法可以从视频数据中获取交通流参数而不丢失关键信息[13, 14]。如图 2(a)所示,在选取的道路断面上标注了到达地点A和离开地点B,两点之间的距离为L。处理数据时,将每辆自行车经过A,B两点的时间分别记为ta和tb。自行车的速度计算公式为v=L/(ta-tb)。同时记录自行车类型(电动自行车或传统自行车)以及自行车位置(位于自行车道或机动车道)。每辆机动车的记录方法同上。
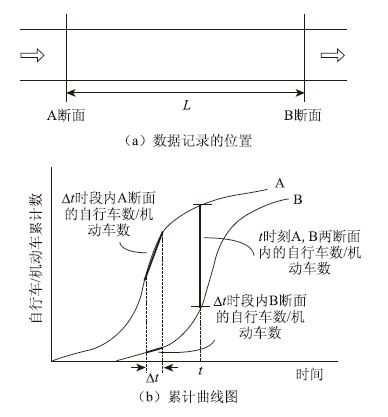 |
| 图 2 累计曲线中的交通流信息 Fig. 2 Traffic flow information in cumulative curves |
根据每个骑行者的到达时间和离开时间,可以分别划出A点和B点的累计曲线,如图 2(b)所示。图中横轴表示时间,纵轴表示在此之前时间段内经过A(B)断面的自行车或机动车的累计数。两条曲线的纵坐标差表示t时刻A,B两断面内的自行车或机动车数,以此来计算密度。曲线斜率表示任意时长Δt内经过A(B)断面的自行车或机动车数,以此来计算流量。通过运用累计曲线法,易于对任意时间段进行数据分析来计算流量和密度。根据时间信息来计算个体机动车速度。
3 广义线性模型建模广义线性模型已广泛应用于许多交通研究[15],是常见的正态线性模型的直接推广,它对因变量的假设条件比线性模型要宽松得多,使得广义线性模型对连续型变量和离散型变量都可以进行拟合。广义线性模型可以处理因变量与解释因素间复杂的特性,大大克服了经典线性模型的局限性;从实用角度看,它比标准的迭代模型更具有效率,其所提供的统计推断功能对重要变量的筛选很有帮助,且模型的假设条件也可得到确认。在实际问题研究中,一个变量往往受到多个重要变量的影响,此时就需要用两个或两个以上的影响因素作为自变量来解释因变量的变化。文中建立广义线性回归模型来预测自行车交通给机动车造成的延误以及其他因素。回归模型的形式要求变量之间的关系(或其转换)本质上是线性的。基本模型公式为:
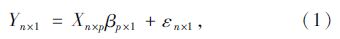
式中,Yn×1为因变量观测值;Xn×p为自变量观测值;βp×1为自变量的相关因素;εn×1为误差项;n为观测的数量;p为预测变量的数量。
运用下面的方程计算因变量的预测值:
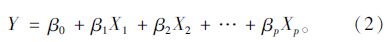
运用最小二乘估计方法来估计广义线性模型中的参数。参数估计的细节见文献[15]。
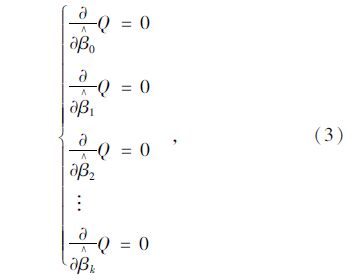
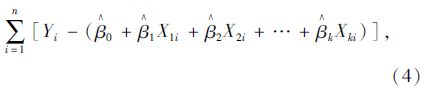
对于多元线性回归模型,方程的总体线性关系显著不等于每个解释变量对被解释变量的影响都是显著的。因此,必须对每个解释变量进行显著性检验,以决定是否作为解释变量被保留在模型中。用于进行变量显著性检验的方法包括:F检验、t检验、Z检验,它们的区别在于构造的统计量不同,应用最多的是t检验。
由于模型参数βi服从下列正态分布:
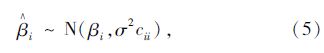
式中,cii为矩阵(X′ X)-1主对角线上的第i个元素;σ2为随机误差项的方差,在实际计算时,用它的估计量代替:
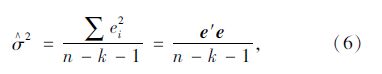
式中e′为矩阵e的转置。
可以构造一个统计量:
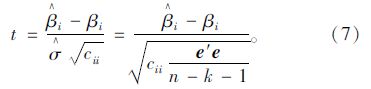
原假设H0:βi=0,预备假设H1:βi≠0,i=1,2,…,k。
给定显著性水平α,可得到临界值tα/2(n-k-1),于是可以根据
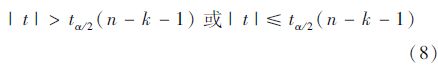
因变量是指机动车交通的延误,自变量是指交通流参数以及其他变量,包括机动车流量、自行车流量、机动车道数、自行车道宽度、电动自行车比例以及路内停车,利用SPSS软件检验确定机动车交通延误与影响因素之间的相关关系。SPSS统计分析过程包括描述性统计、均值比较、一般线性模型、相关分析、回归分析、对数线性模型等几大类。
相关分析是用来度量事物之间或变量之间相关程度强弱的方法,它是研究变量间相关程度的一种常见的统计方法。相关系数是描述相关程度和方向的统计量,用R表示[16]。
检验两个变量的相关性R,两个变量x,y的相关系数的数学表达式为:
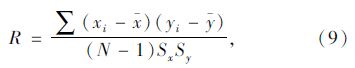
R为两个变量的线性相关系数,即相关强度。R=1表示所有的观察值(点)在二维直角坐标系中都落在一条直线上;R>0表示直线的斜率大于0;R<0表示直线的斜率小于0;R=0表示选取的两个变量无线性相关性。
如果变量x,y间是统计关系,则-1
一般地,相关性的R取值、相关性度量及意义如图 3和表 2所示[17]:
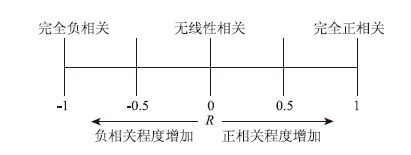 |
| 图 3 相关系数R的取值与性质 Fig. 3 Value and nature of correlation coefficient R |
| |R|的取值范围 | |R|的相关程度 |
| 0.00~0.19 | 极低的相关性 |
| 0.20~0.39 | 低度相关 |
| 0.40~0.69 | 中度相关 |
| 0.70~0.89 | 高度相关 |
| 0.90~1.00 | 极高相关 |
建立模型可以提供信息,以帮助理解各个因素在城市道路上对机动车延误的影响。
4 模型结果分析 4.1 自行车交通流特征分析自行车交通流的关系如图 4所示。由于篇幅限制,且6个位置的自行车交通流的关系的整体趋势一致,故选取6个位置中最具代表性的一个位置,其他位置自行车交通流的关系不再罗列。图 4(a)描述的是每10 s内自行车流量与密度的关系。可以看出,流量随着密度呈线性增长的趋势,这表明自行车交通在道路断面内并不拥挤。图 4(b)描述的是自行车速度与密度的关系。可以看出两个重要特征:(1)随着密度的增加(且流量仍然增加),自行车平均速度略有降低;(2)当密度变大时,自行车速度变化幅度显著下降。这是因为当路段上有许多自行车时,原本速度较快的骑行者被迫匀速前进。这是从不同的城市道路断面中得出一致的结论。
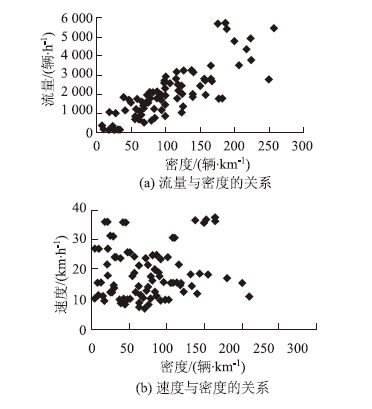 |
| 图 4 自行车交通流各参数之间的关系 Fig. 4 Relationship among various parameters of bicycle traffic |
图 5(a)选择最具代表性的位置描述进入机动车道的自行车辆数。很明显,随着自行车密度的增加,越来越多的自行车进入机动车道。图 5(b)描述了自行车分别在自行车道和机动车道上的平均速度。自行车在机动车道上的平均速度为22.64 km/h,高于在自行车道上的平均速度15.81 km/h。这表明,当自行车道上有较多慢行者时,快行者往往会借助机动车道来超越慢行者,以避免出行延误。图 5(c)描述了电动自行车在自行车道与机动车道的百分比。结果显示,在机动车道上行驶的所有车辆中,电动自行车占87.02%。在自行车道上行驶的大部分是传统自行车,这表明电动自行车与机动车发生潜在碰撞的可能性更大。
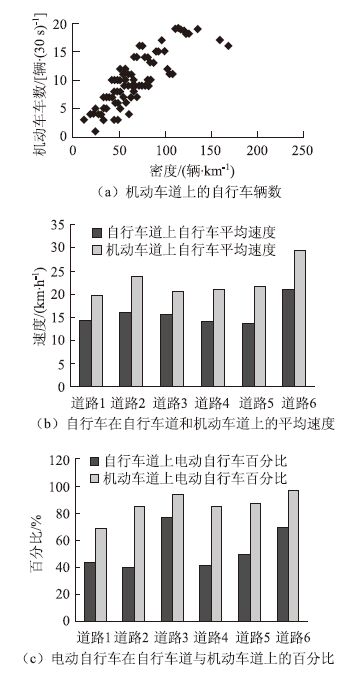 |
| 图 5 行车道与机动车道的交通流特征 Fig. 5 Traffic flow characteristics of bicycle lanes and motor vehicle lanes |
为了分析机动车出行的影响,根据车道将机动车流分为两组,分别为内车道的机动车流和外车道的机动车流。最具代表性的位置为如图 6(a)所示的在不同自行车密度下位于外车道的机动车速度。很明显,自行车流密度对机动车速度影响很大。随着自行车流密度的增加,机动车的平均速度下降。此外,如果周围有大量自行车,驾驶员不愿开得过快而保持低速行驶,所以机动车的速度变化幅度明显降低。最具代表性的位置为如图 6(b)所示的位于内车道的机动车速度。与外车道相比,内车道的机动车速度受自行车流密度的影响较小。随着自行车流密度的增加,机动车的平均速度及速度变化幅度也显著下降。
另一方面需要分析机动车速度与机动车道上自行车数量的关系。类似于图 6,当更多的自行车行驶在机动车道上时,机动车的平均速度及速度变化幅度会下降,这符合一贯的思维。与内车道相比,自行车交通在外车道上对机动车的出行干扰更为严重。这表明,对于只有一条机动车道的道路来说,由于机动车没有其他车道的选择,其机动车与自行车相互干扰的影响更为严重,因而应优先制订政策来改善此类道路的交通出行。当道路上划分了几条机动车道时,机动车受自行车交通的影响较小。
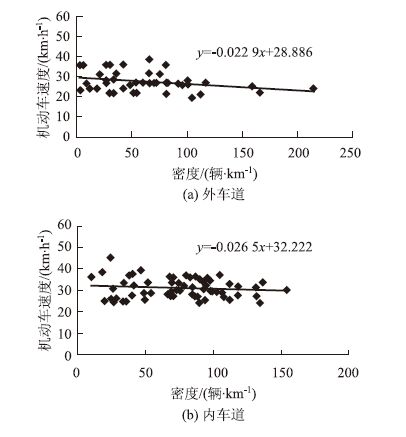 |
| 图 6 不同自行车密度下的机动车速度 Fig. 6 Vehicle speed in different bicycle densities |
本文建立广义线性模型分析机动车延误与自变量之间的关系。以每辆机动车低密度时的速度与自由流时的速度经过该道路所用时间差来计算延误。考虑到一些变量在现实中很难测量,如自行车密度以及在机动车道上行驶的自行车数量,因此模型并不包括这些变量。建立的模型只包括在实际中能够测量的变量,包括机动车流量、自行车流量、机动车道数、自行车道宽度、电动自行车比例及路内停车。
建模结果如表 3所示,可以发现,其中有4个自变量对城市道路的机动车交通延误有显著影响,即自行车流量、机动车流量、机动车道数以及自行车道宽度。根据参数的相关系数可以确定这些变量的影响。从建模结果中也可以看出这些变量是如何影响机动车交通延误的。随着自行车流量的增加,机动车延误也会增加,即自行车流量每增加1 000辆,每辆机动车延误就增加了32.67 s/km。机动车流量每增加1 000辆,每辆机动车延误就增加了38.00 s/km。由于变量系数是负的,所以当机动车道数越多时,对机动车的延误越小。在同样的交通状况下,当机动车道数从1条增加到2条时,机动车延误减少了30.87 s/km。此外,自行车道的宽度与机动车延误呈负相关,这表明自行车道越宽,延误越小。
| 变量 | 系数 | 标准误差 | 检验值 | 显著性 | 95%置信区间 |
| 自行车流量 | 32.67 | 7.67 | 4.29 | <0.001 | [17.33,48.00] |
| 机动车流量 | 38.00 | 8.67 | 4.35 | <0.001 | [20.67,55.33] |
| 机动车道数 | -30.87 | 3.03 | -10.12 | <0.001 | [-36.93,-24.80] |
| 自行车道宽度 | -5.83 | 3.10 | -1.88 | 0.061 | [-12.03,0.367] |
| 常量 | 80.43 | 5.07 | 15.85 | <0.001 | [70.30,90.57] |
| 统计 | 对数似然值=-1 077.782 显著性水平≤0.001 赤池信息量=3.063 | ||||
电动自行车的比例对机动车的延误并没有显著影响,电动自行车进入机动车道的可能性虽然更大,然而结果却与一贯思维不一致。解释这一结果的可能原因是超车需求,对于骑行者进入机动车道的主要原因是自行车交通的速度不同。如果大多数骑行者使用的是电动自行车,那么骑行者之间的速度差异实际上是相当小的。因此,他们可能在自行车道上行驶而不干扰相邻的机动车交通。此外,设置路内停车也并不会对机动车延误造成显著影响。
建模结果也可为相关部门制订政策提供有效信息。图 7为不同交通流下的延误。从图中可以明显看到延误相对于自行车和机动车交通流的变化是如何改变的。如果预估的结果落在不可接受的延误区域,交通部门可以制订政策改善交通出行。此外,当交通状况发生变化时,可以用该模型来预测未来交通出行特征,例如自行车流的需求,也可以运用该模型来评价一些政策对机动车和自行车交通出行的影响,例如增加或减小自行车的宽度,或设置路内停车。
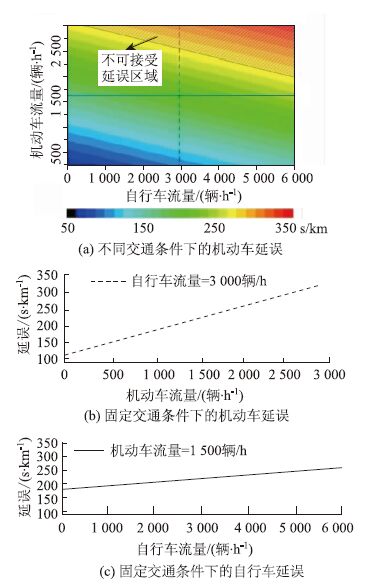 |
| 图 7 不同交通状况下的机动车延误 Fig. 7 Delays of motor vehicle under different traffic |
本文主要分析了自行车交通在机非划线分割道路上对机动车运行造成的影响。研究结果表明,随着自行车密度的增加,自行车的平均速度及速度的变化幅度下降,且更多的自行车进入机动车道。这些自行车的平均速度大于在自行车道上行驶的自行车速度,且电动自行车进入机动车道的可能性更大。随着机动车道上的自行车密度或自行车数量的增加,机动车的平均速度及速度的变化幅度下降。此外,有4个变量对城市道路的机动车交通延误有显著影响,即自行车流量、机动车流量、机动车道数及自行车的宽度。
一些城市道路没有划分自行车道,使得自行车和机动车被迫行驶在同一车道内。在这种情况下,自行车交通对机动车出行的影响与本文不同。文中的模型不可直接用于分析自行车与机动车在同一车道内行驶的交通延误。
| [1] | PUCHER J, BUEHLER R. Why Canadians Cycle More Than Americans: A Comparative Analysis of Bicycling Trends and Policies[J]. |
| [2] | PUCHER J, DILL J, HANDY S. Infrastructure, Programs and Policies to Increase Bicycling: An International Review[J]. |
| [3] | 苏建忠,魏清泉,游细斌.美国的自行车友好社区及其启示[J].国外城市规划,2006,21(3):94-97. SU Jian-zhong, WEI Qing-quan, YOU Xi-bin. American BFC and Its Inspiration for China [J]. Urban Planning International, 2006, 21(3):94-97. |
| [4] | BAI L, LIU P, CHEN Y, et al. Comparative Analysis of the Safety Effects of Electric Bikes at Signalized Intersections[J]. Transportation Research Part D: Transport and Environment, 2013, 20(5):48-54. |
| [5] | CHEN Jing-xu, WANG Wei, LI Zhi-bin, et al. Dispersion Effect in Left-turn Mixed Bicycle Traffic and Its Influence on Capacity of Left-turn Vehicles at Signalized Intersections[J]. |
| [6] | 徐良杰,王炜.左转自行车对直行机动车通行的影响分析模型[J].东南大学学报: 自然科学版,2005,35(5):805-809. XU Liang-jie, WANG Wei. Analysis Model of Influence of Left-turn Bicycle on Passage of Straight-through Vehicles [J]. Journal of Southeast University: Natural Science Edition, 2005,35(5):805-809. |
| [7] | American Association of State Highway and Transportation Officials. Guide for the Development of Bicycle Facilities[M]. Washington, D. C.: AASHTO, 1999. |
| [8] | Transportation Research Board. Highway Capacity Manual[M]. Washington, D.C.: TRB, 2010. |
| [9] | 贾顺平,彭宏勤,郭谨一,等.城市混合交通中自行车对机动车行驶影响的定量分析[J].交通运输系统工程与信息,2008,8(2):58-62. JIA Shun-ping, PENG Hong-qin, GUO Jin-yi, et al. Quantitative Analysis of Impact of Bicycles on Vehicles in Urban Mixed Traffic[J]. Journal of Transportation Systems Engineering and Information Technology, 2008,8(2):58-62. |
| [10] | 陈永恒,王殿海,陶志兴.无物理隔离路段机动车与非机动车速度特性研究[J].交通运输系统工程与信息,2009,9(5):53-57. CHEN Yong-heng, WANG Dian-hai, TAO Zhi-xing. Speed Character Study for Motor Vehicle and Bicycle at Non-barrier Section[J]. Journal of Transportation Systems Engineering and Information Technology, 2009,9(5):53-57. |
| [11] | LI Z, WANG W, LIU P, et al. Physical Environments Influencing Bicyclists' Perception of Comfort on Separated and On-street Bicycle Facilities[J]. |
| [12] | CHEN Xiao-hong, AN Kang, LI Li. Study on Influencing Factors of Bike Lane Capacity[C]// Transportation Research Board 93rd Annual Meeting. Washington, D. C.: TRB, 2014. |
| [13] | CASSIDY M J, MAUCH M. An Observed Traffic Pattern in Long Freeway Queues[J]. |
| [14] | CASSIDY M J, BERTINI R L. Some Traffic Features at Freeway Bottlenecks[J]. |
| [15] | WASHINGTON S P, KARLAFTIS M G, MANNERING F L. Statistical and Econometric Methods for Transportation Data Analysis[J]. Maritime Economics & Logistics, 2003, 46(4):492-493. |
| [16] | 孙逸敏.利用SPSS软件分析变量间的相关性[J].新疆教育学院学报,2007,23(2):120-123. SUN Yi-min. Using SPSS Software to Analyze the Correlation between Variables [J]. Journal of Xinjiang Education Institute, 2007,23(2):120-123. |
| [17] | 阮桂海,蔡建琼,朱志海,等.统计分析应用教程[M].北京:清华大学出版社,2003. RUAN Gui-hai, CAI Jian-qiong, ZHU Zhi-hai, et al. Statistical Analysis Tutorial[M]. Beijing: Tsinghua University Press, 2003. |
 2016, Vol. 31
2016, Vol. 31
