扩展功能
文章信息
- 肖旺, 苏永华, 方砚兵
- XIAO Wang, SU Yong-hua, FANG Yan-bing
- 考虑峰后特性的隧道围岩锚固力学效应
- Anchorage Mechanical Effect of Tunnel Surrounding Rock Considering Post-peak Characteristics
- 公路交通科技, 2016, Vol. 31 (1): 95-102,118
- Journal of Highway and Transportation Research and Denelopment, 2016, Vol. 31 (1): 95-102,118
- 10.3969/j.issn.1002-0268.2016.01.015
-
文章历史
- 收稿日期: 2015-02-09
在隧道开挖过程中应力集中如果超过岩石的峰值强度,会导致岩石峰后软化和峰后体积扩容[1],前者导致围岩承载能力下降,而后者是导致围岩大变形的主要原因。圆形隧洞围岩的变形与压力的弹塑性力学分析最早是由Fenner提出来的,后来Kastner[2]作了重要修正,但他们都假设隧洞围岩为理想弹塑性介质,且认为岩体破坏后无体积变化,这与实际情况具有一定偏差,特别是软弱或破碎岩体隧道的开挖必将导致围岩应变软化和非线性体积膨胀,产生扩容变形。研究结果表明考虑围岩应变软化和塑性扩容更接近实际[3, 4, 5, 6, 7, 8, 9, 10, 11]。苏永华[3]、孙闯[4]基于深部围岩在开挖卸载应力扰动之后其力学性能弱化的现实,认为其应力-应变关系服从峰后软化的节理模型。袁文伯[5]、马念杰[6]考虑岩体的应变软化和塑性流动特性,以岩体的应力-应变峰后破坏段作为岩体的塑性软化强度,建立软化模型,得到了更符合实际、适用性更广泛的巷道围岩塑性区半径和应力的一般解。付国彬[7]、姚国圣[8]、Brown E T和Hoek E[9]同时考虑了围岩应变软化和扩容特性(体积膨胀),基于应力-应变三线段模型,得到了隧道围岩弹塑性解答;范文[10]、Wang[11]基于非关联弹塑性准则,引入剪胀角模拟软岩的塑性扩容特性,研究了围岩扩容的变形、应力解析解。以上成果显著,较接近工程实际。
锚杆在岩体中的作用机制一直是国内外研究的主要问题,并取得了大量研究成果[12, 13, 14, 15]。文竞舟[13]、C. Li和B. Stillborg[14]、Y. Cai[15]等在不考虑岩体塑性软化和体积扩容特性的条件下研究了注浆锚杆与围岩的相互作用及围岩的变形、应力解析。
研究表明,在隧道围岩变形的4个力学分区[1]中,塑性强化区处于峰前变形阶段,是围岩承载的主体;塑性软化区和塑性残余区处于峰后变形阶段,岩体强度已经损伤,是实施支护的主要对象。锚杆支护主要通过外支撑和内加固的形式作用于围岩。外支撑提供径向抗力施加围压,围压的增大会使扩容量随之减弱,因此可以减少体积扩容。内加固一方面通过提高残余区力学参数,降低围岩软化模量;另一方面将锚杆界面的剪应力以体积力[13]的形式引入圆形隧道围岩中。本文在前人研究的基础上考虑峰后围岩变形的应变软化及塑性剪胀扩容特性,基于Mohr-Coulomb强度准则和非关联弹塑性准则,并结合锚杆的加固机理[16],对圆形洞室峰后围岩在锚杆支护作用下进行弹塑性分析,得到了更为全面的应力及变形解答。
1 基本假设和力学模型 1.1 基本力学模型洞室开挖后力学模型如图 1所示:①洞室开挖半径为r0,软化区半径Rp和残余区半径Rb;②锚杆有效锚固长度为L,锚固半径L0=L+r0;③围岩原岩应力场为σz;④把所有作用在围岩表面上的支护阻力pi称为外部支撑,把锚杆与围岩相互黏结的作用力称为内部加固,通过锚杆端部预紧力传递。
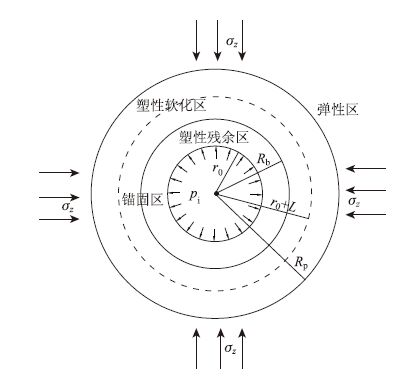 |
| 图 1 围岩弹塑性变形区域图 Fig. 1 Elastic-plastic deformation zone of surrounding rock |
σr,σθ分别为隧道围岩的径向、切向应力;εr,εθ分别为隧道围岩的径向、切向应变。文中上角标为“e”,“p”,“b”分别为弹性区、塑性软化区和塑性残余区的量。
基本假定:(1)认为岩体为各向同性、均质连续介质,无限长圆形隧道可按轴对称平面应变问题处理;(2)锚杆和注浆锚固剂均处于弹性状态,锚杆与围岩完全黏结,不产生滑移。认为注浆体和岩体力学性质一致,只考虑锚杆与围岩的相互作用;(3)在塑性软化区,认为岩体强度随变形发展而衰减主要是由于内聚力变化的结果[1, 5],因此只考虑内聚力的软化和强化,不考虑内摩擦角的软化和强化[7, 8, 9]。
1.2 围岩弹塑性软化与残余模型根据岩体全应力-应变曲线,如图 2(a)所示,其变形可分为弹性区、塑性强化区、塑性软化区和塑性残余区,为了简化,把弹性区和塑性强化区看成峰前弹性变形阶段[1]。
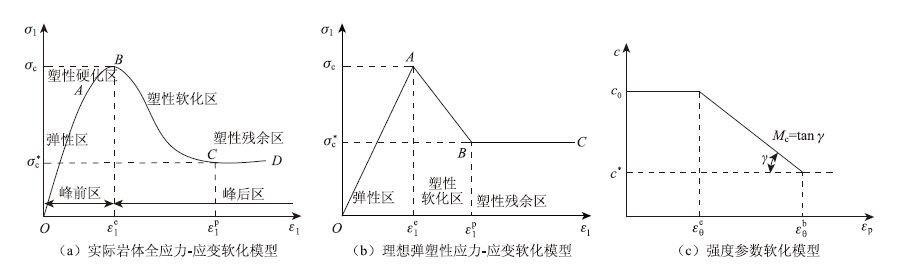 |
| 图 2 围岩峰后软化模型 Fig. 2 Surrounding rock post-peak softening model |
岩石峰后应变软化定律简化为理想残余塑性模型[7, 8, 9, 10, 11],见图 2(b);由研究可知[1, 7, 8, 9]凝聚力c会随着塑性应变的增加而逐渐减小至残余值。假设c随塑性切应变线性软化[1, 7, 8, 9],见图 2(c)。
根据图 2(b),采用线性Mohr-Coulomb准则[1, 7, 8, 9, 10]:
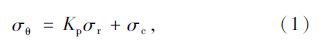
在塑性软化区,式(1)变为:


令软化系数k=Mc ,在围岩残余区,根据式(1)有:
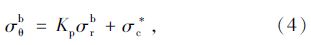
考虑岩体峰后塑性软化区和残余区岩体发生扩容,扩容系数与应变关系[1, 7, 8, 9]如图 3所示。
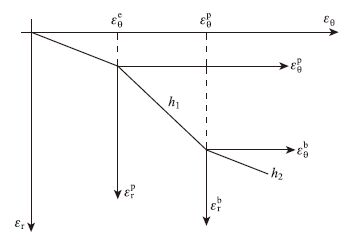 |
| 图 3 围岩峰后扩容模型 Fig. 3 Surrounding rock post-peak dilatancy model |
考虑岩体扩容的非关联流动法则[7, 8, 9, 10, 11],在塑性软化区有:
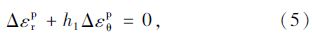
在塑性残余区有:
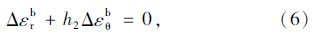
在隧洞围岩中施加锚杆,锚杆对围岩的锚固作用体现在径向和切向的锚固力。径向锚固力对围岩施加围压,围压增大使塑性扩容降低,稳定性增强。锚杆贯穿隧道围岩的软弱面,切向锚固力改善软弱面的力学性质,使围岩抗剪强度参数c,φ提高,残余强度增大,进而降低围岩软化模量。
根据文献[16]锚杆作用机理,在围岩残余区
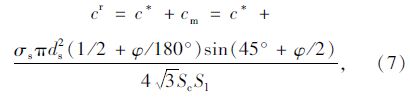
式中,cm为施加锚杆后残余区黏聚力增大值;σs为锚杆屈服强度;ds为锚杆直径;Sc,Sl分别为锚杆沿隧道纵向和横向的布置间距。
施加锚杆后的岩体强度为:

施加锚杆后围岩软化模量为:
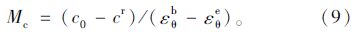
沿锚杆径向的剪应力是由于洞室开挖,围岩变形引起的。通过大量的拉拔试验[14, 15]表明,围岩变形产生剪应力的主要原因是锚杆和围岩之间的相对位移。从测试结果[17, 18]可以看出,当接触面上没有滑移时,即锚杆与岩体完全黏结,锚杆与围岩界面剪应力与剪切位移呈线性增加关系。图 4为锚杆受力图。
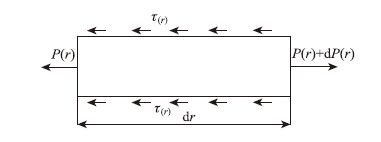 |
| 图 4 锚杆受力图 Fig. 4 Stress analysis of bolt |
如图 4所示,取锚杆轴向微元段,荷载以图示向右为正,τ(r)为锚杆界面剪应力分布,P(r)为锚杆轴力。假定锚固体表面剪应力与剪切位移呈线弹性关系[17, 18],则有:
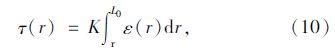

剪应力在锚杆长度上的积分即为轴力分布:
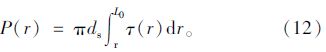
轴向拉应变
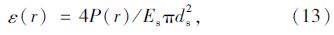
联立式(10)、(12)和(13)有
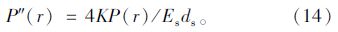
利用边界条件:P(r)|r=r0=P0;P(r)|r=L0=0解得:
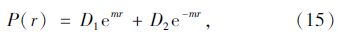
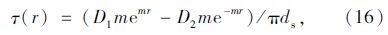
把锚杆对围岩的支护作用力以等效径向体积力f(r)作用于圆形隧道围岩,假设锚杆沿隧道断面对称分布[13],即可分析仅含有单根锚杆的围岩楔形单元体,如图 5所示。
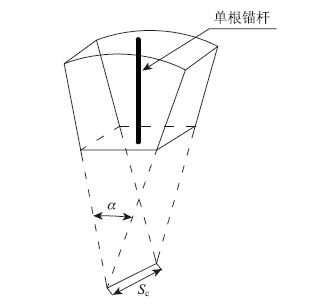 |
| 图 5 锚杆与围岩楔形单元 Fig. 5 Wedge element of bolt and surrounding rock |
如图 5所示,取锚杆微段dr界面上的合力dQ为

此微段的体积dV为:

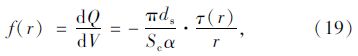
将剪应力表达式(16)代入式(19)即可得到微元体积力f(r)的表达式。
轴对称锚固区内围岩应满足平衡微分方程:
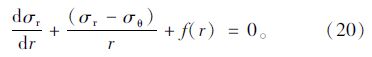
几何方程:
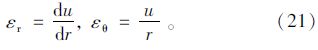
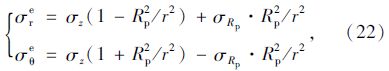
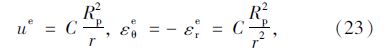
(1)软化区变形与位移
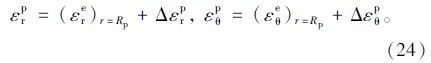
由式(23),(24)及式 (21),(5)得到软化区的位移协调方程:
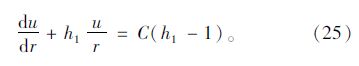
由边界条件ue|r=Rp=CRp,得软化区位移场为:
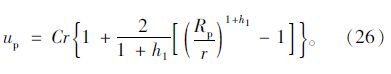
将式(26)代入式(21)可得:
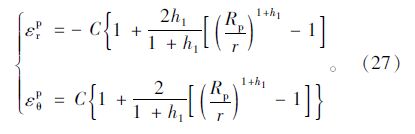
(2)软化区应力
将应变表达式(27)代入式(3),(2)可得
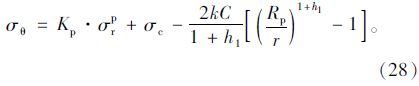
① 无锚杆加固塑性软化区(L+r0≤r<Rp)
联立式(28)与平衡微分式(20),利用边界条件(σer)r=Rp=(σpr)r=Rp,并令 f(r)=0可得塑性区的应力表达式为:
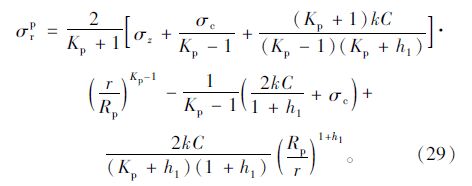
②有锚杆加固塑性软化区(Rb≤r
联立式(28)与(20),利用与无锚杆软化区交接的边界条件(σpr′)r=L0=(σpr)r=L0,可求得
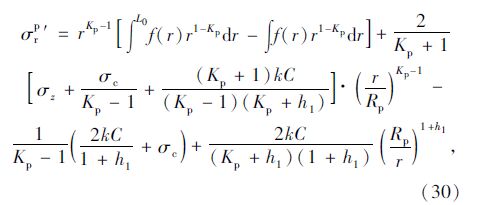
(1)残余区应力,由于锚杆支护,式(4)变为:
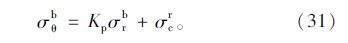
联立式(31)和平衡微分方程(20)并利用边界条件(σr)r=r0=pi,可求得:
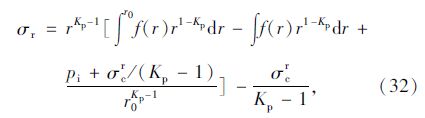

式中积分上的r0表示积分后的原函数用r0代替r。
(2)残余区变形与位移
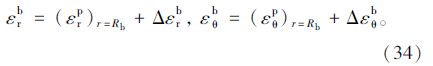
位移的求解过程同上,联立式 (34),(27)和(21),(6)可得

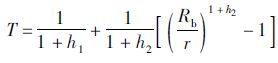 ,下同。
,下同。
将式(35)代入式(21)可得
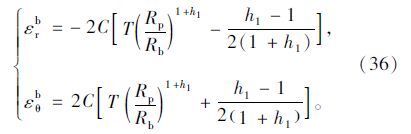
因此,隧洞周边位移u0的解析计算公式为
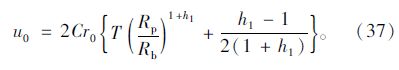
当围岩产生了塑性残余区时,在软化区与残余区交界处,即r=Rb时,软化区岩石强度参数软化至残余强度值,即(σpc)r=Rb=cr代入(3)可得
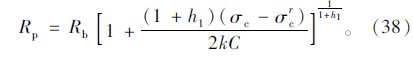
当围岩处于塑性自稳而即将产生残余区的临界状态时,令式(38)中Rb=r0即可。
当围岩处于塑性状态时,塑性区半径由(30)式,将r=r0,σpr′=pi代入计算。
在软化区与残余区交界处,即r=Rb应有应力连续条件有σpr=σbr 由式(30)、(32)可得
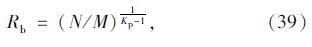
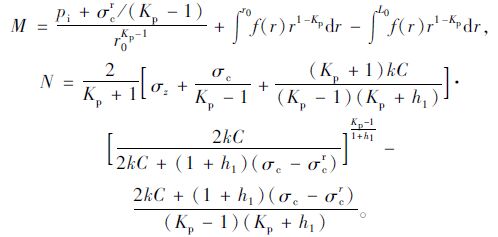
其他形式的外支护塑性软化区和残余区范围求解,令式(39)中f(r)=0,σrc=σ*c即可。
注:文中体积力f(r)的积分涉及到指数积分的求解,本文是根据文献[13]中提到的通过分部积分的方法可得级数展开式:
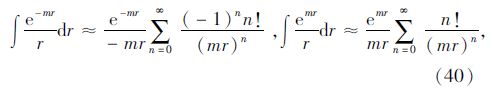
某隧洞半径r0=3 m,所受原岩应力σz=21.8 MPa。软岩的力学性质为:弹性模量Er=Eg=1.4 GPa,泊松比νr=νg=0.32,初始内聚力c0=3.2 MPa,残余内聚力c*=0.23 MPa,内摩擦角φ=30°(由前假定,内摩擦角保持不变)。凝聚力软化模量Mc=600 MPa,剪胀角ψ=10°(h1=1.42),h2=1.4,由于锚杆的加固作用,残余区凝聚力升高至cr=0.52 MPa,软化模量降低至Mc=540 MPa。
锚杆弹性模量Es=210 GPa,有效长度L=1.5 m,直径ds=24 mm,锚杆间纵向和横向间距Sc=Sl=1.2 m,环向夹角α=π/12,锚杆端部预紧力P0=60 kN。
工程中通常在全长黏结锚杆端部托盘(围岩表面)施加预紧力P0[19],锚杆对围岩的作用既有径向的外支撑也有横向的内加固,为了单因素比较说明外支撑和内加固的作用效应,现把锚杆的外支撑支护用等效的钢拱架或混泥土支护阻力替代。
3.1 软化特性对围岩塑性区应力与范围影响由图 6可见,应力峰值点即为塑性区和弹性区区交界点,对应的横坐标即为塑性区半径Rp。不考虑塑性软化的围岩称为状态Ⅰ,对应的Rp=4.712 m;考虑岩石峰后塑性软化的围岩称为状态Ⅱ,对应的Rp=7.897 m,较状态Ⅰ增大了67.6%;在有塑性软化的围岩中施加pi=0.8 MPa的锚杆支护阻力称为状态Ⅲ,对应的Rp=5.024 m,较状态Ⅰ只增大了6.7%,要使状态Ⅱ达到状态Ⅰ需要施加的锚杆支护阻力为pi=1.24 MPa。
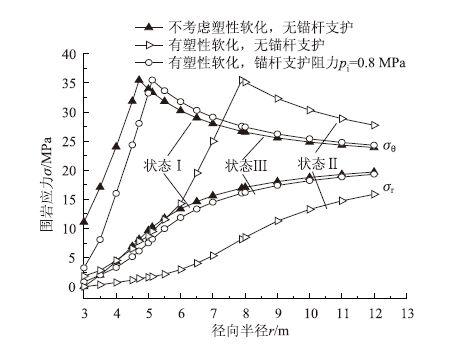 |
| 图 6 软化模量对塑性区应力影响 Fig. 6 Effect of softening modulus on plastic zone stress |
这说明岩石峰后应变软化导致围岩内的应力升高区将由洞壁向围岩深部扩展,围岩承载能力下降,围岩塑性区范围增大。因此在推导围岩塑性区范围时不考虑围岩塑性软化是不精确的。而锚杆的介入降低了围岩软化模量,围岩径向应力、切向应力均增大,应力峰值由围岩深部向洞周扩展,围岩承载能力增大,塑性区范围减少。
3.2 支护特性对围岩塑性区应力与范围影响从图 7可以看出在相同的支护阻力作用下,锚杆支护较等效外支撑围岩的径向应力、切向应力均增大,围岩内应力升高区由围岩深部向洞壁扩展,塑性区不断减小。这说明锚杆支护更能改善围岩应力性质,提高围岩的承载能力。
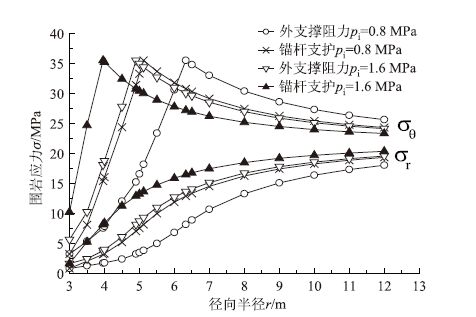 |
| 图 7 锚杆支护与等效外支撑对塑性区应力影响 Fig. 7 Effect of bolting and equivalent outside supporting on plastic zone stress |
从图 8可见,当pi=0.06 MPa时,只有外支撑对应的塑性区半径Rp=6.362 m,残余区半径Rb=4.382 m;锚杆支护对应Rp=5.142 m,Rb=3.409 m;锚杆支护塑性区半径要降低20.0% ,残余区半径要降低22.3%。pi每增大0.06 MPa时,Rp,Rb均减小2%~4%;在同等支护阻力下,锚杆支护对应塑性区半径较外支撑均降低20%~25%,残余区半径均降低22%~30%。
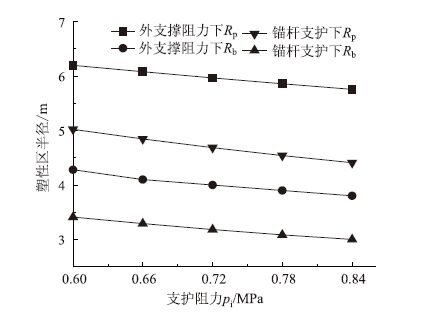 |
| 图 8 锚杆支护与等效外支撑对塑性区范围影响 Fig. 8 Effect of bolting and equivalent outside supporting on plastic zone range |
这说明增加支护阻力均能降低塑性区范围;注浆锚杆内加固控制软化程度,提高残余强度,在同等支护阻力下,效果较外支撑显著。
3.3 扩容特性与支护阻力对围岩塑性区位移影响从图 9可见围岩峰后扩容后体积膨胀,随着剪胀角的增加,扩容程度增加,洞周位移将增大:剪胀角从0°增大到30°时,扩容梯度从1.0增大到3.0,洞周位移从272 mm增加到453 mm,增大到1.7倍。因此必须考虑岩石体积膨胀对隧道围岩收敛的影响。
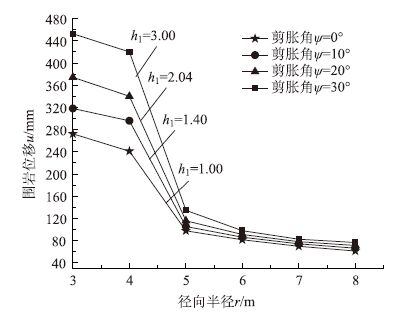 |
| 图 9 剪胀角对位移u的影响 Fig. 9 Effect of dilatation angle on displacement |
随着塑性区径向半径的增加,扩容性影响将减小。这说明扩容特性对塑性残余区位移曲线影响较大,而对塑性软化区和弹性区围岩变形影响较小。
从图 10可以看出,随着支护阻力增大,隧洞周边位移u0明显减小:支护阻力从0.8 MPa增大到2.0 MPa 时,各剪胀角相对应的洞周位移减少幅度均达到50%以上。这说明增加支护阻力可以增大围压,减少围岩扩容,因而能有效控制围岩的变形。
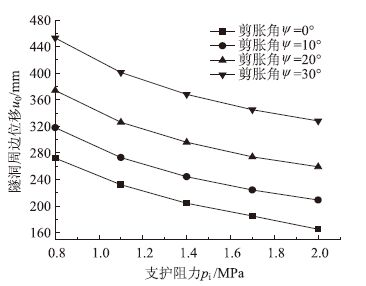 |
| 图 10 支护阻力对洞周位移(u0)的影响 Fig. 10 Effect of support resistance on tunnel surrounding displacement |
本文研究了锚杆对处于峰后状态隧道围岩的锚固效应。具体获得了如下几方面的成果:
(1)基于锚杆锚固抗剪支护力学机制,提出了支护效应的等效体积力模型,建立了考虑支护抗力的围岩平衡微分方程。
(2)导出了峰后状态围岩在注浆锚杆支护下的围岩应力、洞壁位移、塑性软化区及塑性残余区半径的计算表达式。
(3)岩石峰后塑性软化使应力升高区向深部转移,使围岩塑性区范围增大;而剪胀扩容影响隧道残余区收敛。
(4)结合算例对比,定量揭示了锚杆支护对峰后围岩力学状态、变形发展的控制效应;识辨出了锚杆内加固、外支撑对围岩峰后特征的不同改良机制。
| [1] | 何满潮, 景海河, 孙晓明. 软岩工程力学[M].北京:科学出版社, 2002. HE Man-chao, JING Hai-he, SUN Xiao-ming. Engineering Mechanics of Soft Rock Mass [M]. Beijing: Science Press, 2002. |
| [2] | 于学馥, 郑颖人, 刘怀恒, 等. 地下工程围岩稳定性分析[M].北京:煤炭工业出版社, 1983. YU Xue-fu, ZHENG Ying-ren, LIU Huai-heng, et al. Analysis on Stability of Surrounding Rock of Underground Structure[M]. Beijing: China Coal Industry Publishing Housing, 1983. |
| [3] | 苏永华, 郑璇. 深部节理岩体分区破裂化机制数值研究[J]. 公路交通科技,2013, 30(1): 94-101. SU Yong-hua, ZHENG Xuan. Numerical Study on Mechanism of Zonal Disintegration in Deep Rock Mass with Joints[J]. Journal of Highway and Transportation Research and Development, 2013, 30(1): 94-101. |
| [4] | 孙闯, 张向东, 贾宝新. 基于收敛-约束法的隧道围岩安全性评价[J]. 公路交通科技, 2014, 31(3): 96-100. SUN Chuang, ZHANG Xiang-dong, JIA Bao-xin. Evaluation of Tunnel Surrounding Rock Safety Based on Convergence-constraint Method[J]. Journal of Highway and Transportation Research and Development, 2014, 31(3): 96-100. |
| [5] | 袁文伯, 陈进. 软化岩层中巷道的塑性区与破碎区分析[J]. 煤炭学报, 1986, 11(3): 77-85. YUAN Wen-bo, CHEN Jin. Analysis of Plastic Zone and Loose Zone around Opening in Softening Rock Mass [J]. Journal of China Coal Society, 1986, 11(3): 77-85. |
| [6] | 马念杰, 张益东. 圆形巷道围岩变形压力新解 法[J]. 岩石力学与工程学报,1996,15(1): 84-89. MA Nian-jie, ZHANG Yi-dong.A New Analysis on Ground Pressures around Openings[J]. Chinese Journal of Rock Mechanics and Engineering,1996, 15(1): 84-89. |
| [7] | 付国彬. 巷道围岩破裂范围与位移的新研究[J]. 煤炭学报,1995,20(3):304-310. FU Guo-bin. Recent Investigation of Extent of Fractured Zone and Displacement of Rocks around the Roadways [J]. Journal of China Coal Society,1995,20(3):304-310. |
| [8] | 姚国圣, 李镜培, 谷拴成. 考虑岩体扩容和塑性软化的软岩巷道变形解析[J]. 岩土力学, 2009,30(2):463-467. YAO Guo-sheng, LI Jing-pei, GU Shuan-cheng. Analytic Solution to Deformation of Soft Rock Tunnel Considering Dilatancy and Plastic Softening of Rock Mass[J]. Rock and Soil Mechanics,2009,30(2):463-467. |
| [9] | BROWN E T, BRAY J W, LADANYI B, et al. Ground Response Curves for Rock Tunnels[J]. |
| [10] | 范文, 俞茂宏, 陈立伟, 等. 考虑剪胀及软化的洞室围岩弹塑性分析的统一解[J]. 岩石力学与工程学报,2004, 23(19): 3213-3220. FAN Wen, YU Mao-hong, CHEN Li-wei, et al. Unified Elastoplastic Solution for Surrounding Rocks of Openings with Consideration of Material Dilatancy and Softening[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(19): 3213-3220. |
| [11] | WANG Y. Ground Response of Circular Tunnel in Poorly Consolidated Rock[J]. |
| [12] | 何忠明, 林杭. 节理岩体边坡稳定性的锚杆支护影响分析[J]. 公路交通科技, 2010, 27(11): 8-12,19. HE Zhong-ming, LIN Hang. Influence of Bolt Reinforcement on Stability of Rock Jointed Slope[J]. Journal of Highway and Transportation Research and Development, 2010,27(11): 8-12,19. |
| [13] | 文竞舟, 张永兴, 王成. 隧道围岩全长黏结式锚杆界面力学模型研究[J]. 岩土力学, 2013, 34(6):1645-1652. WEN Jing-zhou, ZHANG Yong-xing, WANG Cheng. Study of Mechanical Model of Fully Grouted Rock Bolt's Anchorage Interface in Tunnel Surrounding Rock[J]. Rock and Soil Mechanics,2013, 34(6):1645-1652. |
| [14] | LI C, STILLBORG B. Analytical Models for Rock Bolts[J]. |
| [15] | CAI Y, ESAKI T, JIANG Y J. A Rock Bolt and Rock Mass Interaction Model [J]. |
| [16] | 朱浮声, 郑雨天. 全长粘结式锚杆的加固作用机理分析[J]. 岩石力学与工程学报, 1996,15(4):333-337. ZHU Fu-sheng, ZHENG Yu-tian. Support Action Analysis of Tensioned and Grouted Bolts[J]. Chinese Journal of Rock Mechanics and Engineering,1996, 15(4): 333-337. |
| [17] | 张季如, 唐保付. 锚杆荷载传递机理分析的双曲函数模型[J].岩土工程学报,2002,24(2):188-192. ZHANG Ji-ru, TANG Bao-fu. Hyperbolic Function Model to Analyze Load Transfer Mechanism on Bolts[J]. Chinese Journal of Geotechnical Engineering, 2002,24(2): 188-192. |
| [18] | GURUNG N. 1-D Analytical Solution for Extensible and Inextensible Soil/rock Reinforcement in Pull-out Tests[J]. |
| [19] | 韦四江,勾攀峰. 锚杆预紧力对锚固体强度强化的模拟实验研究[J]. 煤炭学报, 2012,37(12):1987-1993. WEI Si-jiang,GOU Pan-feng. Analogy Simulation Test on Strengthening Effect for Pretention of Bolts on Anchorage Body[J]. Journal of China Coal Society, 2012,37(12):1987-1993. |
 2016, Vol. 31
2016, Vol. 31
