扩展功能
文章信息
- 陈忆前, 陈艾荣, 马如进
- CHEN Yi-qian, CHEN Ai-rong, MA Ru-jin
- 台风环境下海上结构的设计风浪联合概率模型
- A Joint Probabilistic Model of Design Wave and Wind Parameters for Offshore Structures under Typhoon Circumstances
- 公路交通科技, 2016, Vol. 31 (1): 89-94
- Journal of Highway and Transportation Research and Denelopment, 2016, Vol. 31 (1): 89-94
- 10.3969/j.issn.1002-0268.2016.01.014
-
文章历史
- 收稿日期: 2015-01-20
2. 招商局重庆交通科研设计院有限公司, 重庆 400067
2. China Merchants Chongqing Communications Technology Research & Design Institute, Co., Ltd., Chongqing 400067, China
海上结构物主要受风、海浪等可变作用力作用。规范[1]中涉及风、浪的计算时,当有较长期波浪实测资料时,可选出某一累积频率波高的年最大值系列进行频率分析,确定不同重现期的设计波高;当无较长期测波资料时,则根据当地的风速资料间接确定不同重现期的设计波浪。第1种方法虽然能够得到较准确的设计波高,但是未明确风影响因素,无法从设计角度加以考虑;第2种方法以风速的重现期为波浪的重现期,与事实不尽相符。有研究[2]根据风速和有效波高同步观测资料,用Gumbel逻辑模型来拟合风速和有效波高的联合分布,在有风、浪同步数据的情况下不失为一种好方法,但未将海浪周期纳入研究。
本文研究建立在某大桥所在地海洋站(下文简称海洋站)2001—2003年的海浪短期观测资料基础上,将海面波动、风都作为随机过程考虑。为方便研究,还作了以下的简化和假设:
(1)对象海域处于同一天气形势下,风场的宏观结构相同;
(2)海域足够大,不考虑近岸影响;
(3)水深足够大,忽略水深对海浪的影响;
(4)海浪考虑综合效应,不分风浪、涌浪,忽略波群;
(5)忽略考虑海(潮)流的影响。
本文在一些已有研究的基础上,取长补短,将台风环境下海上结构主要承受作用的关键要素风速、浪高和浪周期结合起来进行概率分析,推导出相应的概率分布模型,据此计算出基于台风环境的设计波浪要素,即使在缺乏长期观测数据的情况下,也能为海上结构设计提供可参考的设计参数。
1 短期测波资料频率分析波浪的表示通常采用波高H及与该波高对应的跨零周期T。对于不规则的波浪,常用波高统计特征值有[1, 2, 3, 4]:同一波系所有波高平均值H,波系前1/3大波波高平均值H1/3(亦称有效波高HS),前1/10大波波高平均值H1/10,累积频率为1%的波高H1%;对于波周期,也有相应的所有周期平均值T,1/3大波各波高对应周期的平均值T1/3(TS),T1/10等。深水条件下,各特征值有如下换算关系[1, 2, 3, 4, 5]:
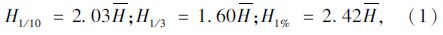
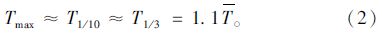
对该海洋站的实测波高特征值H1/10进行分级统计[6],采用截尾正态分布[7]对该波高累积频率点进行拟合,其拟合分布模型为:
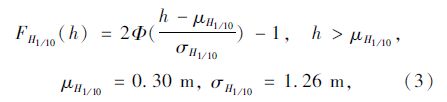
式中参数μH1/10,σH1/10由极大似然估计法算出。截尾正态分布函数的估计值有如下表达式:
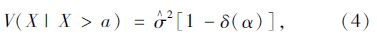
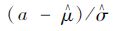 =0,λ(α)=Φ(α)/[1-Φ(α)]=
=0,λ(α)=Φ(α)/[1-Φ(α)]=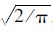 ,δ(α)=λ(α)[λ(α)-α]=2/π,Φ(·)为标准正态分布概率密度函数,Φ(·)为标准正态累积分布函数。解以上方程可得
,δ(α)=λ(α)[λ(α)-α]=2/π,Φ(·)为标准正态分布概率密度函数,Φ(·)为标准正态累积分布函数。解以上方程可得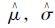 。
。
波高累积频率点及其截尾正态分布拟合曲线如图 1所示,图中横坐标为波高h,纵坐标为波高h的累积分布函数,无量纲。
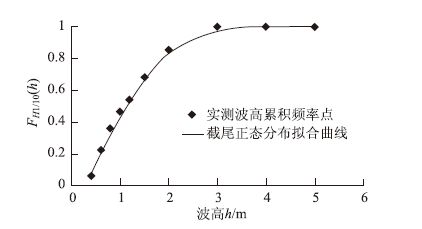 |
| 图 1 波高拟合分布曲线 Fig. 1 Fitting distribution curve of wave height |
同理,对同期波浪周期特征值T1/10进行分级统计,采用对数正态分布进行拟合,其拟合分布模型为:
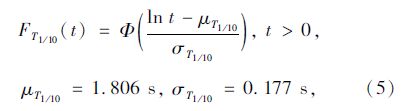
式中μT1/10,σT1/10同上由极大似然估计法算出。波浪周期累积频率点及其对数正态分布拟合曲线如图 2所示,图中横坐标为波浪周期t,纵坐标为周期t的累积分布函数,无量纲。
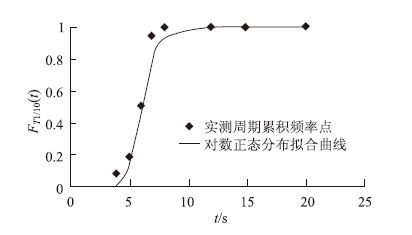 |
| 图 2 周期拟合分布曲线 Fig. 2 Fitting distribution curve of wave period |
采用Kolmogorov-Smirnov法对以上拟合进行检验,计算结果表明:在显著性水平α=0.05时波高分布能通过假设检验;在显著性水平α=0.01时周期分布能通过假设检验。
2 给定风速条件下的设计波高、周期 2.1 风速分布模型风速概率分布模型采用应用得最为广泛的双参数Weibull分布,其累积分布函数形式如下:
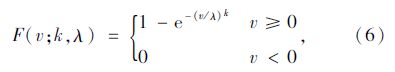
式中,k为形状参数;λ为尺度参数。在缺乏该地同期风观测实时记录的情况下,需借助一些间接方法估算k,λ。
假设各年风速观测值独立同分布,其累积分布函数FV(v)与风速年极值累积分布函数FVmax(v)当FV(v)→1时,存在以下关系:FV(v)≈[FVmax(v)]1/N,N为N年。根据海洋站1976—2005年30 a风速年极值所得桥址处的基本风速,按式(6)计算可得桥址处风速观测值(地面或水面以上10 m高度处10 min平均风速)累积分布函数值FV(v)如表 1所示。
| 重现期/a | 10 | 20 | 50 | 100 |
| 基本风速V/(m·s-1) | 36.5 | 38.8 | 41.5 | 43.3 |
| FVmax(v) | 0.90 | 0.95 | 0.98 | 0.99 |
| FV(v) | 0.996 5 | 0.998 3 | 0.999 3 | 0.999 7 |
选用表 1中FV(v)更趋于1的后两组数值(v,FV(v))代入式(6),即可得k=2.15,λ=16.46风速累积分布曲线见图 3,图中横坐标为风速V,纵坐标为风速V的累积分布函数,无量纲。
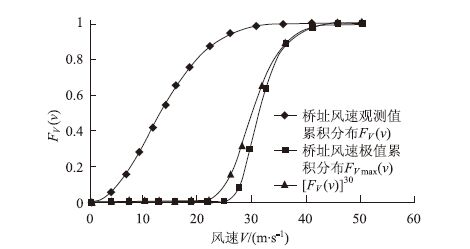 |
| 图 3 风速分布曲线 Fig. 3 Distribution curve of wind velocity |
若视风速V大于某一阈值v0的事件为泊松过程,则在时间间隔[t0,t0+τ]内n次出现事件A={V≥v0}的概率为:
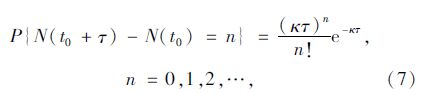
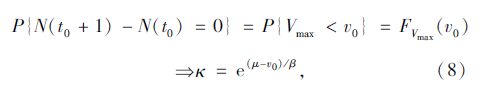
当v0为12级台风风速32.7 m/s时,κ=0.422 y-1。
2.2 风速条件V≥v0下的波高、周期联合概率分布根据Nataf变换原理[8, 9],波高、波周期、风速标准正态化见式(9):
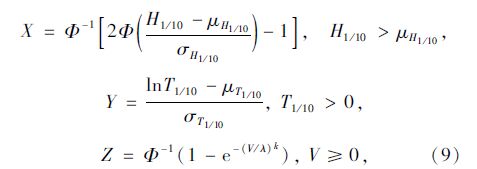
并认为波高X与风速Z相关,有ρXZ,认为波周期Y与风速Z不相关,即ρYZ=0。由式(9)可得一定风速条件V≥v0下的波高、周期联合概率密度函数[3]:
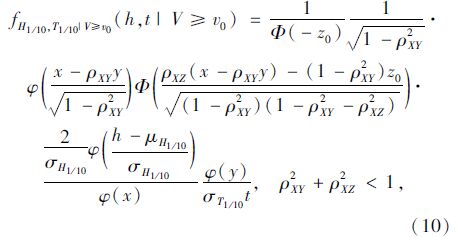
以上推导过程主要参考文献[3]。
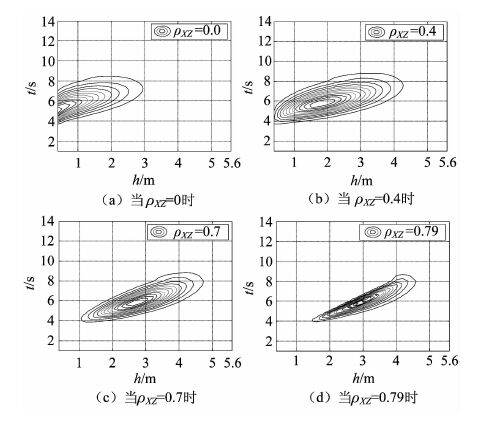 |
| 图 4 fH1/10,T1/10|V≥v0(h,t|V≥v0)等概率曲线随ρXZ变化趋势 Fig. 4 Probability curves of fH1/10,T1/10|V≥v0 (h,t|V≥v0)varying with ρXZ |
同一波系n个波高中的最大波高Hmax满足极值Ⅰ型分布,累积分布函数[4]为:
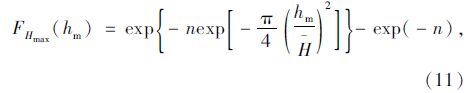
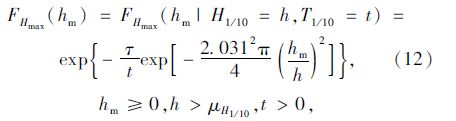
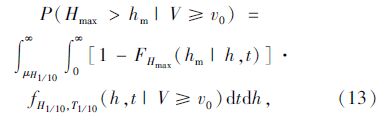
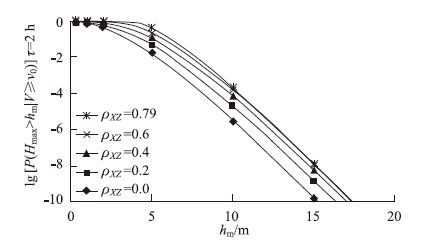 |
| 图 5 台风持续时间内最大波高Hmax随ρXZ变化的超值概率曲线 Fig. 5 Overflow probability curves of maximal wave height Hmax varying with ρXZ during a typhoon event |
风速条件V≥v0下的最大波高{Hmax(t)| V≥v0,0≤t≤T}可作为滤过复合Poisson过程,如图 6所示。图中横坐标为时间t,纵坐标为最大波高Hmax考虑表示为:
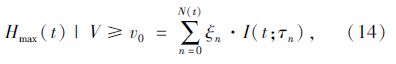
式中,{N(t),t∈[0,T]}为一以κ为强度的Poisson过程,其值由式(8)确定;ξn(n=1,2,…。)为第n个出现的风速条件最大波高值,它们是独立同分布于FHmax|V≥v0(hm|V≥v0)的随机变量序列,且与N(t)独立,并令ξ0=0。
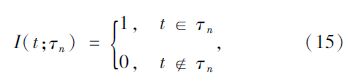
式中,τn(n=1,2,…。)为第n个出现的风速条件最大波高所持续的时间。记Tn(n=1,2,…。)为ξn-1出现到ξn出现所需的时间,且τnTn,并令τ0=0。
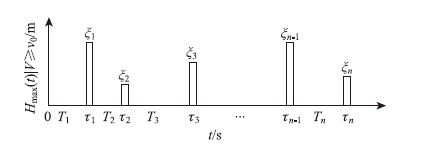 |
| 图 6 滤过复合Poisson过程样本函数示意图 Fig. 6 Schematic diagram of sample function of filtered composite Poisson process |
则N年内一定风速条件最大波高HmaxN|V≥v0=max0≤t≤NHmax(t)|V≥v0的超值概率[11]是:
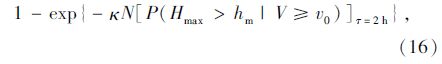
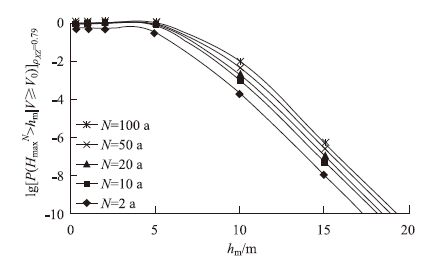 |
| 图 7 台风下ρXZ=0.79的N年最大波高 HmaxN随N变化的超值概率曲线 Fig. 7 Overflow probability curves of maximal wave height HmaxN during N years under typhoon event varying with N (ρXZ=0.79) |
为了计算给定风速条件下与特征波高对应的波浪周期,可推导出周期在一定波高条件下的条件概率密度函数见式(17):
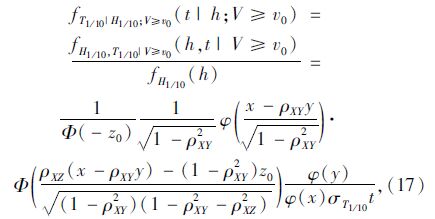
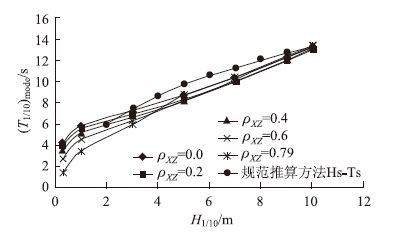 |
| 图 8 台风下H-Tmode随ρXZ变化曲线 Fig. 8 Curves of H-Tmode under typhoon event varying with ρXZ |
对于设计特征波的波高,规范[1]规定,强度设计应采用H1%;中国1982年和1983年分别制定的《海上移动式钻井船入级与建造规范》[12]和《海上固定平台入级与建造规范》[13]规定,设计波高采用最大波高的众值(Hmax)mode。本文针对台风环境这一极端情况进行研究,如果按常规取H1%难免偏于保守,因此,应着眼于最大波高Hmax。
对式(14)取N为1 a,给定某一概率值p即可求得相应重现期(1/p)下的年最大波高Hmax1。令式(16)对hm两次求导等于0,可解得重现期为N年的最大波高众值(Hmax)mode。取Hmax1,(Hmax)mode中较大者作为设计特征值波高,结合式(17)、式(2)通过一系列转换:Hmax→H→H1/10[4]→T1/10→T,可得特征波浪周期。如果ρXY=0.6,v0=32.7 m/s,则台风时不同ρXZ的设计波浪要素见表 2,同时,亦列出H1%值[4]作为比较。重现期一般取为50 a,设计周期采用T[1]。
| ρXZ | 重现期/a | H1% /m | Hmax1/m | (Hmax)mode/m | (T1/10)mode/s | T/s |
| 0.0 | 10 | 2.42 | 2.65 | 3.02 | 6.6 | 6.0 |
| 20 | 2.92 | 3.41 | 3.63 | 6.9 | 6.3 | |
| 50 | 3.53 | 4.24 | 4.37 | 7.2 | 6.6 | |
| 100 | 3.96 | 4.79 | 4.89 | 7.5 | 6.8 | |
| 0.2 | 10 | 3.11 | 3.43 | 3.88 | 6.7 | 6.1 |
| 20 | 3.61 | 4.23 | 4.49 | 6.9 | 6.3 | |
| 50 | 4.22 | 5.09 | 5.23 | 7.3 | 6.6 | |
| 100 | 4.66 | 5.65 | 5.76 | 7.5 | 6.9 | |
| 0.4 | 10 | 3.77 | 4.22 | 4.69 | 6.7 | 6.1 |
| 20 | 4.25 | 5.01 | 5.27 | 7.0 | 6.4 | |
| 50 | 4.85 | 5.86 | 6.00 | 7.4 | 6.7 | |
| 100 | 5.28 | 6.41 | 6.51 | 7.7 | 7.0 | |
| 0.6 | 10 | 4.37 | 4.99 | 5.43 | 6.9 | 6.3 |
| 20 | 4.81 | 5.73 | 5.96 | 7.3 | 6.6 | |
| 50 | 5.37 | 6.51 | 6.63 | 7.7 | 7.0 | |
| 100 | 5.78 | 7.02 | 7.11 | 8.0 | 7.3 | |
| 0.79 | 10 | 4.87 | 5.66 | 6.01 | 7.6 | 6.9 |
| 20 | 5.26 | 6.29 | 6.47 | 8.1 | 7.4 | |
| 50 | 5.77 | 6.97 | 7.06 | 8.6 | 7.8 | |
| 100 | 6.13 | 7.42 | 7.49 | 8.8 | 8.0 |
本文以2001—2003年短期测波资料作为分析依据,其中包含该海洋站所在地经历的两次台风袭击,在台风资料匮乏的条件下,具有一定的代表性,更为重要的是,提出这样一种思路的分析方法。
3 结论海上结构传统设计一般单独考虑风、海浪,得到一定重现期下的设计特征值,与实际情况不符。本文通过对短期测波资料进行概率分析,建立概率模型并作出拟合分布曲线。建立风速概率分布模型,从随机过程的角度求出台风下强度κ=0.422 y-1。
进而推导了给定风速条件下的波高、周期概率分布模型,其分布规律为:波高、风速相关系数ρXZ越大,波高越大,周期值区间越小。引入滤过复合Poisson过程来模拟风浪联合作用过程,推导出给定风速条件下N年最大波高概率分布,周期条件概率分布,借此推算出一定重现期下的最大波高众值(Hmax)mode作为设计特征波高,周期平均值T作为设计特征周期。与传统方法相比,明确了风速这一重要影响因素并作为设计参数之一,对海上结构设计方法是一次新的尝试。
| [1] | JTJ 213—98,海港水文规范[S]. JTJ 213—98,Code of Hydrology for Sea Harbour[S]. |
| [2] | 周道成,段忠东.耿贝尔逻辑模型在极值风速和有效波高联合概率分布中的应用[J].海洋工程,2003,21(2):45-51. ZHOU Dao-cheng,DUAN Zhong-dong. The Gumbel-logistic Model for Joint Probability Distribution of Extreme-value Wind Speeds and Effective Wave Heights[J]. The Ocean Engineering,2003,21(2): 45-51. |
| [3] | DITLEVSEN O. Stochastic Model for Joint Wave and Wind Loads on Offshore Structures[J]. Structural Safety,2002,24(2002): 139-163. |
| [4] | 邱大洪.波浪理论及其在工程中的应用[M].北京:高等教育出版社,1985:155,158-170. QIU Da-hong. Wave Theory and Its Application in Engineering[M]. Beijing: Higher Education Press,1985: 155,158-170. |
| [5] | 竺艳蓉.海洋工程波浪力学[M].天津:天津大学出版社,1991:184-185. ZHU Yan-rong. Ocean Engineering Wave Mechanics[M]. Tianjin: Tianjin University Press,1991: 184-185. |
| [6] | 李远林.波浪理论及波浪载荷[M].广州:华南理工大学出版社,1994:255-257. LI Yuan-lin. Wave Theory and Wave Loads[M]. Guangzhou: South China University of Technology Press,1994: 255-257. |
| [7] | COHEN A C. Estimating the Mean and Variance of Normal Populations from Singly Truncated and Doubly Truncated Samples[J]. |
| [8] | DER KIUREGHIAN A,LIU P L. Structural Reliability under Incomplete Probability Information[J]. |
| [9] | LIU P L,DER KIUREGHIAN A. Multivariate Distribution Models with Prescribed Marginals and Covariances[J]. |
| [10] | GHOSN M,MOSES F. Design of Highway Bridges for Extreme Events[R]. Washington,D.C.: Transportation Research Board,2003. |
| [11] | 李扬海.公路桥梁结构可靠度与概率极限状态设计[M].北京:人民交通出版社,1997. LI Yang-hai. Highway Bridge Reliability and Probabilistic Limit State Design[M]. Beijing:China Communications Press,1997. |
| [12] | 中华人民共和国船舶检验局.海上移动式钻井船入级与建造规范[S].北京:人民交通出版社,1982. Register of Shipping of PRC. Rules for the Classification and Construction of Mobile Offshore Drilling Units[S]. Beijing: China Communications Press,1982. |
| [13] | 中华人民共和国船舶检验局.海上固定式平台入级与建造规范[S].北京:人民交通出版社,1983. Register of Shipping of PRC. Rules for the Classification and Construction of Fixed Offshore Platforms[S]. Beijing: China Communications Press,1983. |
 2016, Vol. 31
2016, Vol. 31
