扩展功能
文章信息
- 王永宝, 赵人达, 徐腾飞, 占玉林
- WANG Yong-bao, ZHAO Ren-da, XU Teng-fei, ZHAN Yu-lin
- 钢管混凝土轴压构件徐变简化计算方法研究
- Study on Simplified Creep Calculation Method of CFST Members under Axial Loading
- 公路交通科技, 2016, Vol. 31 (1): 57-63
- Journal of Highway and Transportation Research and Denelopment, 2016, Vol. 31 (1): 57-63
- 10.3969/j.issn.1002-0268.2016.01.009
-
文章历史
- 收稿日期: 2015-06-04
高速铁路上列车的行驶速度较高,对大跨度桥梁结构的平顺性要求较高,钢管混凝土拱桥以其独特的优势在现代高速铁路的建设中得到广泛的应用。钢管核心混凝土的收缩徐变会引起大跨度钢管混凝土拱桥产生较大的竖向位移和应力重分布,这将会显著影响高速铁路的安全性和舒适性。因此准确分析钢管混凝土结构的收缩徐变特征,对保证高速铁路上大跨度钢管混凝土拱桥的正常运营具有重大理论和实践意义。
国内外相关学者对钢管混凝土结构的收缩徐变进行了大量的试验与理论研究,分析了混凝土时变作用对钢管混凝土轴心受压构件长期变形的影响。对钢管混凝土轴压构件长期变形计算的理论研究成果有YAMADA[1]和ICHINOSE[2]开尔文链模型,HAN L H[3, 4]、YANG Y F [5]和UY[6]等的按照龄期调整的有效模量法模型,韩冰和王元丰[7, 8]等的继效流动模型,王玉银[9, 10]等的逐步积分法模型,赵金钢[11]等的等效温度荷载法模型,WASSIM[12]提出的钢管对核心混凝土的紧箍力以及钢管和核心混凝土屈服的增量计算模型等。韩冰[13]和GENG Y[14]对钢管混凝土徐变计算方法进行了对比分析,探讨了各个预测模型的计算精度。综合比较以上分析方法可以看出,开尔文链模型[1, 2]的参数需要试验拟合,不适合初步设计采用;按照龄期调整的有效模量法和继效流动模型需要进行较多的迭代计算;等效温度荷载法需要建立有限元模型,比显式计算方法复杂。各个学者给出的钢管混凝土长期变形的分析方法有较大差异[13, 14],在保证精度的前提下,进一步简化钢管混凝土的徐变计算方法还需要深入研究。
为了提高计算速度,简化计算过程,便于设计人员采用,本文根据钢管混凝土徐变的特点,对按照龄期调整的有效模量法[3]和逐步积分法[10]计算公式进行了简化,并与传统分析结果进行了对比分析,探讨了修正的ACI209模型[15]、CEB90模型[16]、GL2000模型[17]、EC2模型[18]对预测精度的影响;针对钢管混凝土的密封性较好,相对湿度的取值与普通混凝土有较大差别的特点,进一步分析了CEB90模型和EC2模型选择不同相对湿度对预测结果的影响,并给出了这两种预测模型的相对湿度取值范围。
1 徐变简化计算模型在钢管混凝土轴压构件受到外界荷载较小时,钢管对核心混凝土的紧箍力较小,可以忽略不计[2, 7, 11, 19]。在不考虑钢管对核心混凝土的紧箍力作用时,任意时刻tk,截面上满足内力平衡条件和变形协调条件:
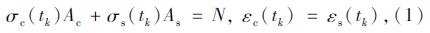
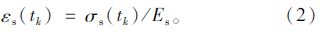
当初始荷载施加后k=0时,混凝土材料满足胡克定律:
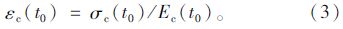
由式(1)~(3)可以计算得到初始加载后t0时刻核心混凝土的应力:
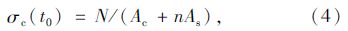
式中,σc(tk),εc(tk)为tk时刻核心混凝土的应力和应变;σs(tk),εs(tk)为tk时刻钢管的应力和应变;n=Es/Ec(t0)为钢管和核心混凝土弹性模量比值;N为钢管混凝土截面上承担的轴力;Ac,As分别为核心混凝土和钢管的截面面积;Es,Ec(t0)分别为钢管和核心混凝土的弹性模量。
混凝土在变应力状态下的徐变计算方法有拟合公式法[1, 2]、按照龄期调整的有效模量法[3, 4, 5, 6],继效流动准则方法[ 7-8]、老化理论方法[9, 10, 11]。拟合公式法计算简单,但是需要试验数据进行参数拟合,推广性较差,不适合桥梁结构的初步设计采用;按照龄期调整的有效模量法和逐步积分法简单,计算精度能够满足设计要求;继效流动准则方法需要考虑钢管对核心混凝土的紧箍力作用,并进行大量的迭代,计算方法复杂,对设计人员计算能力要求较高。鉴于此,本文分别选取按照龄期调整的有效模量法[20]和老化理论作为变应力状态下核心混凝土徐变计算方法。以下分别用两种方法推导钢管混凝土徐变计算公式。
1.1 按照龄期调整的有效模量法变应力状态下核心混凝土的徐变计算公式采用BAZANT教授提出按照龄期调整的有效模量法[20],考虑混凝土的徐变后,任意时刻tk核心混凝土的应变可以表示为:
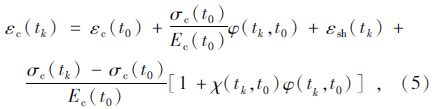
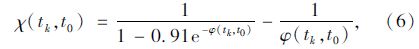
式中,φ(tk,t0)为加载龄期为t0,计算龄期为tk时混凝土的徐变系数;εsh(tk)为计算龄期为tk时混凝土的收缩应变;χ(tk,t0)为加载龄期为t0,计算龄期为tk时混凝土的老化系数,按式(6)计算[3]。
核心混凝土发生徐变以后,由式(1)和(2)可以得到tj时刻核心混凝土的应力和应变关系:
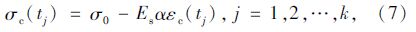
式中,σ0=N/Ac,α=As/Ac。
将式(7)代入式(5),可以得到按照龄期调整的有效模量法计算的tk时刻钢管混凝土的显式徐变应变计算公式:
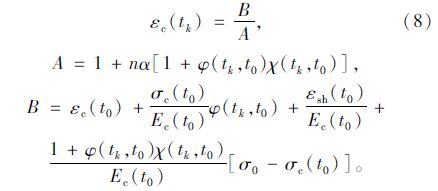
式(8)即为采用按照龄期调整的有效模量法给出的钢管混凝土徐变的简化计算公式。
1.2 逐步积分法变应力状态下钢管核心混凝土的徐变计算公式采用老化理论,将时间离散为t0,t1,…,tk时间点,当时间间隔Δti足够小时,计算公式为:
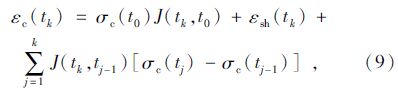
任意时刻tk截面上还满足内力平衡和变形协调条件,将式(7)代入式(9)中可以得到采用逐步积分法计算的tk时刻钢管混凝土的显式徐变应变计算公式:
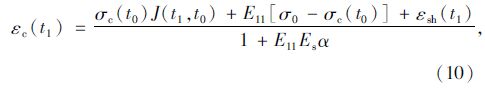
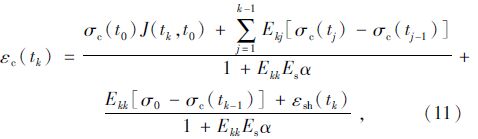
目前大多数混凝土的收缩徐变预测模型,如ACI209模型、CEB90模型、EC2模型和GL2000模型,直接给出的是徐变系数表达式
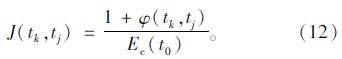
为了进一步简化计算公式,将式(12)代入式(10)、(11)中,可以得到由徐变系数表示的钢管混凝土的徐变计算公式:
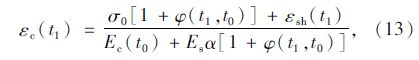
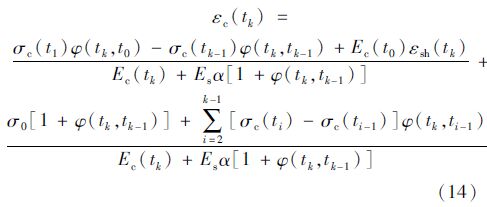
式(13)、(14)即为用徐变系数表示的逐步积分法钢管混凝土徐变的简化计算公式。采用本公式可以通过tk时刻以前的核心混凝土的应力和徐变系数,直接计算tk时刻钢管混凝土的应变值,大大简化了计算过程。
2 徐变简化计算模型验证为验证本文提出的简化分析方法的正确性,以文献[9]给出的钢管混凝土轴心受压构件为对象,进行了钢管混凝土长期变形计算。混凝土的徐变预测模型采用CEB90模型,取密封状态下混凝土的相对湿度为98%,构件理论厚度按照实际的计算方法确定,不考虑核心混凝土的收缩。分别用式(8)、(13)、(14),文献[3, 10, 11]给出的公式计算钢管混凝土轴压构件的长期变形,并将结果进行对比分析。不同公式给出的结果对比情况见表 1,具体截面尺寸见表 2的VП试件。由表可知,式(8)与文献[3]的计算结果相差较小,两组试件的徐变应变差小于2 με,完全可以满足初步设计的要求,但是本文提出的显式计算方法简单,计算速度快,不需要大量的迭代。式(13)~(14)和文献[10]的徐变应变相差小于4 με,计算结果相差不大,满足工程要求,但式(10)、(11)用单个徐变函数代替了平均徐变函数,简化了文献[10]中的Ec1k和Ec2kj的计算。由于目前大多数徐变模型直接给出的是徐变系数的表达式,将式(10)、(11)简化为可以直接代用徐变系数进行计算的式(13)、(14),进一步简化了计算过程。
图 1给出了采用不同方法计算所得的钢管混凝土轴心受压构件的徐变应变与试验结果的对比情况,由图可知,上述5种方法的计算结果与试验结果相差不大,这与文献[14]中的结论是一致的。按照龄期调整的有效模量法(式(8)和文献[3])的计算结果偏高,但是此方法可以直接计算任意时刻tk的徐变应变,不需要计算tk时刻以前的徐变应变;逐步积分法(式(13)、(14)和文献[10])的计算结果比按照龄期调整的有效模量法偏小,比等效温度荷载法偏大,但是需要计算tk时刻以前的徐变应变;等效温度荷载法(文献[11])的计算结果 偏低,除需要计算tk时刻以前的应变以外,还需要建立有限元模型,计算方法较前两种方法复杂。式(13)、(14)计算结果介于按照龄期调整的有效模量法和等效温度荷载法之间,计算方法相对简单,不需要将徐变模型计算的徐变系数转化为徐变函数,计算精度与其他方法一致,鉴于以上优点,本文选择式(13)、(14)作为钢管混凝土徐变计算公式。
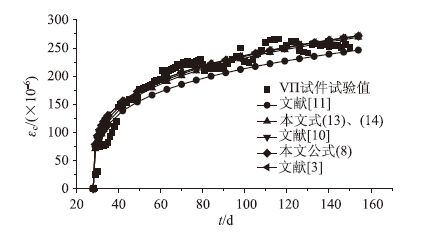 |
| 图 1 不同计算方法的试件徐变计算值对比图 Fig. 1 Comparison of calculated creep curves of CFST members obtained by different calculation methods |
以上分析结果表明:用徐变系数表示的逐步积分法简单,且精度较高。基于试验结果,采用CEB90模型、EC2模型、GL2000模型和修正的ACI209模型分析钢管混凝土轴心受压构件的徐变。CEB90模型、EC2模型、GL2000模型相对湿度取98%;ACI209模型的极限徐变系数用1.5代替文献[15]给出的2.35[6],相对湿度取98%,一般情况下内填混凝土添加减水剂后坍落度较大,可以取200 mm。计算试件取表 2的VП试件。
| 编号 | D(B)/mm | tt/mm | L/mm | Es/GPa | Ec/GPa | fcm/MPa | α/% | N/kN | t0/d |
| Ι[9] | 140.00 | 2.63 | 420.0 | 179.00 | 14.80 | 20.70 | 7.96 | 303.0 | 5 |
| П[9] | 140.00 | 2.62 | 420.0 | 179.00 | 29.40 | 23.60 | 7.93 | 304.0 | 7 |
| Ш[9] | 140.00 | 2.62 | 420.0 | 179.00 | 33.10 | 37.20 | 7.93 | 290.0 | 27 |
| V[9] | 140.00 | 2.60 | 420.0 | 179.00 | 33.10 | 37.20 | 7.86 | 441.0 | 30 |
| VП[9] | 140.00 | 2.60 | 420.0 | 179.00 | 33.10 | 37.20 | 7.86 | 515.0 | 29 |
| CR-40-4.5[2] | 100.12 | 4.36 | 396.0 | 184.96 | 17.12 | 13.57 | 19.99 | 103.9 | 28 |
| CR-40-3.2[2] | 100.12 | 3.12 | 396.0 | 191.61 | 17.12 | 13.57 | 13.74 | 103.9 | 28 |
| CR-80-3.2[2] | 99.96 | 3.12 | 796.5 | 191.61 | 17.12 | 13.57 | 13.76 | 103.9 | 28 |
| CR-V-80-4.5b[3] | 165.20 | 4.50 | 1 000.0 | 214.00 | 30.40 | 39.10 | 11.86 | 173.0 | 28 |
| R-2[21] | 100(60) | 2.93 | 600.0 | 195.00 | 29.20 | 29.70 | 17.72 | 304.0 | 28 |
| CFST[6] | 90.00 | 3.00 | 270.0 | 200.00 | 43.25 | 52.00 | 14.80 | 180.0 | 14 |
| CFST-XB-4[22] | 140.00 | 2.20 | 350.0 | 205.00 | 35.50 | 35.50 | 6.59 | 235.3 | 28 |
| 注:D(B)为圆钢管截面外径或方形、矩形钢管截面长和宽; tt为钢管壁厚度;L为钢管混凝土试件高度;Es和Ec分别为钢管和核心混凝土的弹性模量;fcm为圆柱体混凝土28 d的轴心抗压强度;N为钢管混凝土施加的轴压荷载;t0为钢管混凝土的加载龄期;α为钢管混凝土的含钢率。 | |||||||||
图 2给出了不同混凝土徐变预测模型计算的钢管混凝土长期变形随时间的变化曲线,由图可知:GL2000模型早期徐变发展较快,后期变化缓慢,与试验结果偏差较大,这与文献[11]的计算结果一致;ACI209模型经过修正后,计算结果与实测结果吻合程度有所提高,但是对不同的试件,都有明显高估或低估徐变应变的趋势,且ACI209模型对湿度的敏感性较差[24],即使进行湿度或者体积系数的修正,其计算结果与湿度假定为98%的计算结果相差不大; EC2模型和CEB90模型计算结果与试验结果吻合最好。以上分析表明EC2模型和CEB90模型可以作为钢管混凝土徐变计算的预测模型。
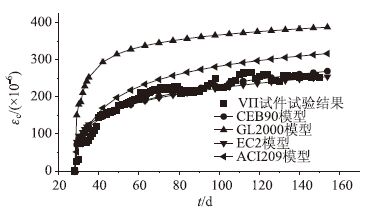 |
| 图 2 不同徐变模型的试件徐变计算值对比 Fig. 2 Comparison of calculated creeps of CFST members obtained by different creep models |
EC2模型和CEB90模型的相对湿度显著影响预测结果,且目前对钢管混凝土徐变模型相对湿度取值范围的研究较为欠缺,为了分析EC2模型和CEB90模型计算中相对湿度的取值问题,本文以既有的试件为分析对象,选取相对湿度h为70%,90%,95%和98%作为计算参数,分析相对湿度取值对钢管混凝土徐变计算预测精度的影响。表 2给出了不同加载龄期,承受不同荷载大小的方钢管、矩形钢管混凝土和圆钢管混凝土试件。本次选取的构件包括普通混凝土和膨胀混凝土,混凝土强度变化范围13~52 MPa,含钢率为6.6%~20%,加载龄期为5~34 d。
图 3给出了4种不同湿度的EC2模型和CEB90的分析结果与试验结果对比情况。由图可知,CEB90模型和EC2模型对相对湿度敏感性较大,当相对湿度取大气平均湿度70%时,计算结果明显高估试验值,证明钢管核心混凝土受到钢管的密闭作用,其湿度较高,明显大于外界大气相对湿度;当相对湿度取90%时,短龄期加载试件与试验结果吻合较好,见图 3(f)和(g);当相对湿度取95%时,28 d 加载试件与试验结果吻合较好,见图 3(c),(h)~(k);当相对湿度取98%时,28 d加载试件与试验结果吻合较好,见图 3(d)。而28 d加载试件在相对湿度取95%时,短期预测结果与试验结果吻合较好,见图 3(b)、(c)。而长期试验结果的徐变值突然增加,究其原因可能是调整荷载时荷载增加导致的,其试验值明显高于计算值。14 d加载试件CFST受外界温度影响较大,其长期变形呈现较大的增长速度。文献[10, 11] 认为CEB90模型和EC2模型计算时h应为无穷,但是经计算显示h取为无穷计算得到徐变系数与相对湿度取98%计算的结果相差不大。从图 3可以看出,如果只取构件理论厚度为无穷(即相对湿度取98%),大多数试件的徐变计算值小于试验值,该方法明显低估了短龄期加载试件混凝土的徐变。因此,本文建议构件理论厚度按照原有的计算方法计算,但是相对湿度取值范围取90%~ 98%。
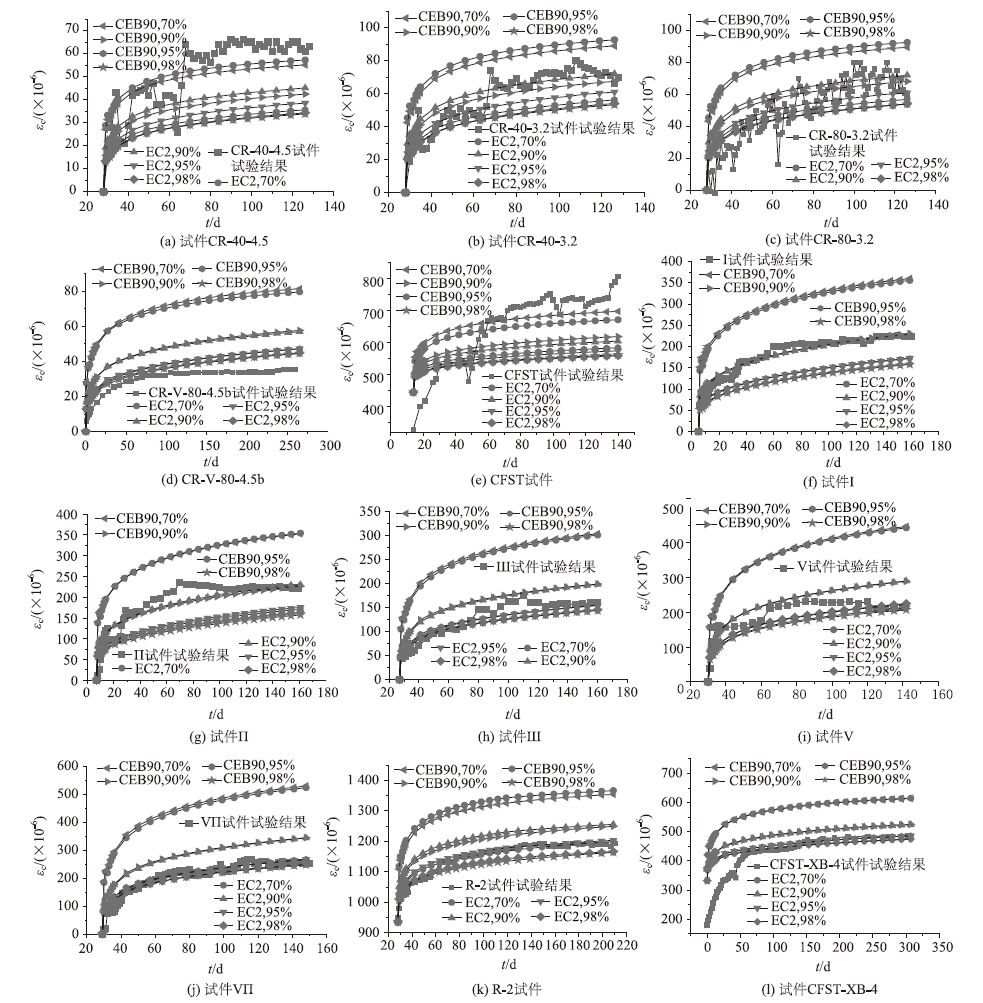 |
| 图 3 钢管混凝土构件长期荷载作用下徐变应变计算值与试验值对比 Fig. 3 Comparison of calculated and tested creep strains of CFST members under long-term loading |
当湿度取90%时,短龄期加载的试验结果与分析结果吻合较好;当湿度取98%时,长龄期加载的试验结果与分析结果吻合较好。而实际的钢管混凝土的湿度应该随着时间的推移逐渐减小,以上结论与实际不符,究其原因,可能是短龄期加载的钢管混凝土徐变试件较少,计算结果不具有代表性,也可能还有其他因素能够显著影响短龄期和长龄期加载的钢管混凝土的徐变,具体原因还需要进一步探讨与分析。
5 结论钢管混凝土的徐变受初始应力、徐变预测模型、变应力状态下核心混凝土计算公式以及基本假定的影响较大,本文分析了钢管混凝土徐变的特点,基于按照龄期调整的有效模量法和逐步积分法简化了钢管混凝土轴压构件的徐变计算公式,可以直接利用显式计算公式计算钢管混凝土的徐变,极大地简化了计算过程,运用本文计算公式对钢管混凝土长期变形进行了分析,将计算结果与试验结果进行了对比分析,得到如下结论:
(1)基于按照龄期调整的有效模量法和逐步积分法推导的钢管混凝土轴压构件徐变简化计算公式,其计算结果与试验结果吻合较好,可供工程应用参考。
(2)钢管混凝土的徐变受混凝土徐变模型相对湿度取值影响较大,大量事实表明:相对湿度取值范围为90%~98%的CEB90模型和EC2模型在分析低应力状态下的钢管混凝土轴压构件的徐变时,具有较高的精度。
| [1] | YAMADA C, MORINO S, KAWAGUCHI J, et al. Creep Behavior of Concrete-Filled Steel Tubular Members[R]. Mie, Japan: Mie University, 1995: 83-98. |
| [2] | ICHINOSE L H,WATANABLE E, NAKAI H. An Experimental Study on Creep of Concrete Filled Steel Pipes[J]. |
| [3] | HAN L H, TAO Z, LIU W. Effects of Sustained Load on Concrete-filled Hollow Structural Steel Columns[J]. Journal of Structural Engineering, 2004, 130(2): 1392-1404. |
| [4] | HAN L H, YANG Y F. Analysis of Thin-walled Steel RHS Columns Filled with Concrete under Long-term Sustained Loads[J]. |
| [5] | YANG Y F. Behaviour of Recycled Aggregate Concrete Filled Steel Tubular Columns under Long-Term Sustained Loads[J]. |
| [6] | UY B, DAS S. Time Effects in Concrete-Filled Steel Box Columns in Tall Buildings[J]. |
| [7] | 韩冰,王元丰. 钢管混凝土轴心受压短柱的徐变分析[J]. 铁道学报, 1999,21(6):87-90. HAN Bing, WANG Yuan-feng. Study on Creep of Concrete Filled in Steel Tubular Members under Axial Loading[J]. Journal of the China Railway Society, 1999,21(6):87-90. |
| [8] | 王元丰,韩冰. 徐变对钢管混凝土轴心受压短柱紧箍应力影响分析[J].铁道学报,2000,22(增1):92-94. WANG Yuan-feng, HAN Bing. Influence of Creep on Confining Stress of Axially Compressed Concrete Filled Steel Tubular Short Columns[J]. Journal of the China Railway Society, 2000,22(S1):92-94. |
| [9] | WANG Y Y, GENG Y, RANZI G, et al. Time-dependent Behaviour of Expansive Concrete-filled Steel Tubular Columns[J]. |
| [10] | 王玉银, 耿悦, 张素梅. 钢管微膨胀混凝土轴压短柱长期变形研究[J]. 中国公路学报, 2011,24(6):57-63. WANG Yu-yin, GENG Yue, ZHANG Su-mei. Research on Long-term Deformation of Concrete-filled Steel Tubular Stubs with Expansive Additive under Axial Loading[J]. China Journal of Highway and Transport, 2011,24(6):57-63. |
| [11] | 赵金钢,赵人达,占玉林. 钢管混凝土轴心受压构件徐变计算方法及徐变模型对比分析[J]. 公路交通科技, 2013,30(4): 46-52. ZHAO Jin-gang, ZHAO Ren-da, ZHAN Yu-lin. Comparative Analysis of Creep Calculation Methods and Creep Models for Axially Compressed CFST Members[J]. Journal of Highway and Transportation Research and Development, 2013,30(4): 46-52. |
| [12] | NAGUIB W, MIRMIRAN A. Creep Modeling for Concrete-filled Steel Tubes[J]. |
| [13] | 韩冰, 王元丰. 圆钢管混凝土轴心受压构件徐变分析的比较[J]. 中国公路学报, 2007, 20(2): 83-86. HAN Bing, WANG Yuan-feng. Creep Analysis Comparison of Circular Axially Compressed Concrete-filled Steel Tubular Members[J]. China Journal of Highway and Transport, 2007,20(2):83-86. |
| [14] | GENG Y,RENZIG WANG Y, et al. Time- dependent Behaviour of Concrete-filled Steel Tubular Columns: Analytical and Comparative Study[J]. |
| [15] | American Concrete Institute. ACI Committee 209, Prediction of Creep, Shrinkage and Temperature Effects in Concrete Structures[S]. Detroit: American Concrete Institute, 1992. |
| [16] | Comite Euro-International Du Beton, CEB-FIP Model Code 1990[S]. Lausanne: Thomas Thelford, 1993. |
| [17] | GARDNER N J, LOCKMAN M J. Design Provisions for Drying Creep and Shrinkage of Normal Strength Concrete[J]. ACI Materials Journal, 2001, 98(2): 159- 167. |
| [18] | BS EN 1992-1-1:2004, Eurocode 2: Design of Concrete Structures [S] |
| [19] | UY B. Static Long-Term Effects in Short Concrete-filled Steel Box Columns under Sustained Loading[J]. ACI Structural Journal, 2001,98(1) :96-104. |
| [20] | BAZANT Z P. Prediction of Concrete Creep Effects Using Age: Adjusted Effective Modulus Method[J]. ACI Journal & Proceedings, 1972, 69: 212-217. |
| [21] | 王戎令,王起才,马丽娜,等. 膨胀剂掺量和应力比对钢管混凝土徐变性能的影响[J]. 中南大学学报:自然科学版,2014,45(7).2416-2423. WANG Rong-ling, WANG Qi-cai, MA Li-na, et al. Effect of Interaction between Expanding Agent Proportion and Stress Ratio on Creep Characteristics of Concrete Filled Steel Tube[J]. Journal of Central South University:Science and Technology Edition,2014,45(7):2416-2423. |
| [22] | KWON S H,KIM T H,KIM J K,et al. Long-term Behaviour of Square Concrete-Filled Steel Tubular Columns under Axial Service Loads[J]. |
| [23] | HOWEL R W, LARK R J, BARR B I G. A Sensitivity Study of Parameters Used in Shrinkage and Creep Prediction Models[J]. |
 2016, Vol. 31
2016, Vol. 31
