扩展功能
文章信息
- 王雁, 穆春阳, 马行
- WANG Yan, MU Chun-yang, MA Xing
- 基于Zernike不变矩与SVM的交通标志的识别
- Traffic Sign Recognition Based on Zernike Invariant Moment and SVM
- 公路交通科技, 2015, Vol. 31 (12): 128-132
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (12): 128-132
- 10.3969/j.issn.1002-0268.2015.12.021
-
文章历史
- 收稿日期: 2015-01-20
汽车的飞速发展,为人们日常生活的出行提供了便利,但也带来了各种问题,交通拥堵,交通事故频频发生。欧洲致力于提高道路行驶安全性的组织[1]高度评价了交通标志的良好可视性在避免车辆发生不幸中起到的重要性。因此,交通标志识别系统得到了广泛的关注,系统可以实时准确地将道路信息传递给驾驶员,有效地帮助驾驶员对可能的危险做出预测,从而实现安全驾驶。 交通标志识别系统分为检测和识别两部分,检测部分对输入系统的图像进行定位,确定是否存在交通志标志;识别部分对检测到的交通标志进行分类,确定其属于特定的交通标志种类。国内外对交通标志的识别已经做了大量的研究,目前采用的识别算法有模板匹配和神经网络识别,但是识别结果受图像的旋转和部分遮挡等的影响较大[2, 3]。也有采用SURF特征值进行模板匹配的识别方法[4, 5],试验结果表明,模板匹配易于实现,但是其扩展性比较差,不具备学习能力。对基于Hu不变矩和BP网络的识别算法[6, 7],大量研究表明,Hu不变矩的识别能力低于Zernike不变矩,尤其对于旋转图像的识别准确率较低[8]。本文对德国公开交通标志标准识别库(GTSRB)中的10种常见交通标志进行识别,直接对感兴趣区域进行处理。首先对感兴趣区域进行预处理,然后提取预处理后图像的Zernike和Hu不变矩特征向量值,最后将特征向量值分别输入SVM进行识别。
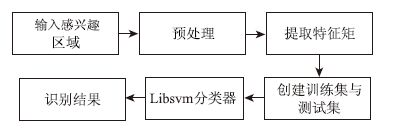
本文提出的交通标志识别算法如图 1所示。
|
| 图 1 交通标志识别算法框图 Fig. 1 Block diagram of traffic sign recognition algorithm |
不变矩由Hu[9]在1962年提出,并推导了7个几何不变矩,定义二维(M×N)图像为{f(x,y),x,y=0,…,M-1},则整幅图像的(p+q)阶矩mpq定义为:
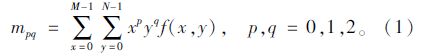
若满足f(x,y)在(x,y)平面上非零,则存在上式定义的各阶原点矩。图像的原点矩不是平移不变矩,图像的中心矩是平移不变矩,则大小为M×N的图像f(x,y)的中心矩upq为:
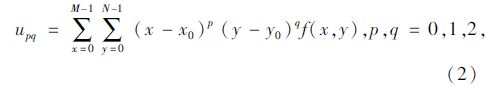
式中x0,y0为几何矩的中心,x0=m10/m00,y0=m01/m00。 对几何中心矩upq进行规则化,得到几何中心矩δpq具有不变性,规则化定义为:
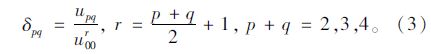
对于二维f(x,y)图像的(p+q)阶中心矩进行非线性组合生成7个不变矩:

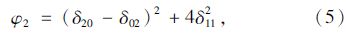
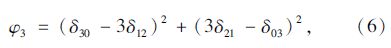
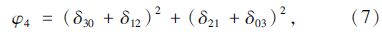
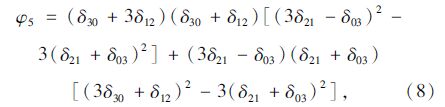
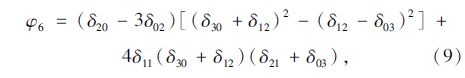
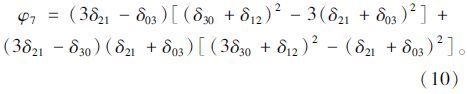
Zernike不变矩[10]是Teague于1980年提出了正交多项式不变矩,定义二维图像f(x,y)的(m+n)阶Zernike不变矩为Zmn,得到:
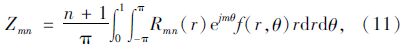
式中,m为正整数或负整数;n为正整数或零,且满足n-|m|为偶数和n+|m|的条件限制;Rmn为点(x,y)的径向多项式;f(r,θ)为函数f(x,y)在极坐标下的对应函数,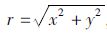 ,-1
,-1
对于一个二维图像,其Zernike矩Zmn是复数,将其实部记作Cmn,虚部记作Smn,分别得到:
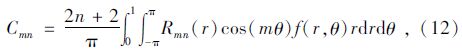
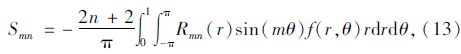
式中m≥0,n≥0。设图像旋转一个角度之后的Zernike矩由原来的Zmn变为Z′mn,并且它们的关系满足Z′mn=Zmnejmθ,可以推导出Zernike矩的幅值没有发生变化,即Zernike矩在离散条件下具有而Hu矩不具有的旋转和缩放不变性。
采用Zernike矩提取交通标志限速的特征值,提取其在6种环境下的7个Zernike不变矩。6种环境如图 2所示,包括旋转、缩放等条件下的图像。提取结果如表 1所示。

|
| 图 2 6种环境下的限速标志 Fig. 2 Speed limit signs in 6 environments |
| 编码 | Zerniek1 | Zernike2 | Zernike3 | Zernike4 | Zernike5 | Zernike6 | Zernike7 |
| 1 | 0.230 63 | 0.004 726 6 | 0.000 927 62 | 0.067 922 | 0.566 01 | 5.3113 | 0.668 45 |
| 2 | 0.233 5 | 0.003 609 | 0.000 974 42 | 0.067 961 | 0.566 34 | 5.3176 | 0.668 83 |
| 3 | 0.235 06 | 0.003 389 9 | 0.000 845 27 | 0.069 478 | 0.562 56 | 5.3177 | 0.683 76 |
| 4 | 0.236 95 | 0.003 964 5 | 0.000 605 72 | 0.070 377 | 0.566 47 | 5.3123 | 0.682 61 |
| 5 | 0.232 95 | 0.003 492 9 | 0.000 673 07 | 0.067 976 | 0.566 46 | 5.3187 | 0.688 98 |
| 6 | 0.237 78 | 0.003 951 2 | 0.000 850 83 | 0.070 172 | 0.564 76 | 5.3188 | 0.680 59 |
对表 1进行分析可知,图像缩放旋转的7个Zernike不变矩和标准图像特征的误差在(10-4,10-6)范围内,误差非常小,可以证明本文提出的Zernike矩具有缩放和旋转不变性。
2 支持向量机(SVM)近年来,在模式识别中越来越多地使用机器学习方法来构建分类器,并取得了较好的分类效果。目前,机器学习法是交通标志识别的主流方法,其中SVM具有完善的理论基础和更好的分类性能,应用更为广泛。本文采用SVM进行特征值的分类,最终实现交通标志的识别。
2.1 SVM理论介绍SVM最早由Vapnik于1992年提出[11]。利用核函数解决寻找非线性变换函数,可以将特征向量映射到更高维空间实现线性的分类。其基本思想是找出能同时满足将2类不同的数据样本正确分开的分类线,满足使训练错误率最小,且分类间隔最大。设数据集为S,可得:
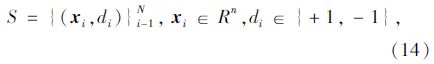
式中,xi为特征向量;di为特征向量对应的类别;N为正整数。
线性判别函数的一般形式为:
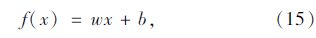
式中,w为线性判别函数的权值;b为其中的常数项。 对应分类面的判别函数式为:

将判别函数进行归一化,使2类所有的样本都满足|f(x)|>=1, 要求分类面对所有的样本都能正确分类,需要满足:
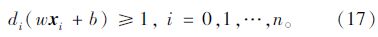
最佳超平面可以通过几何间隔最大化来找到,但为了处理方便,可以将其转化为优化问题为:
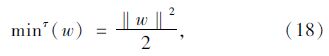
式中τ为线性判别函数因子。
为了便于分析处理,引入拉格朗日乘数:
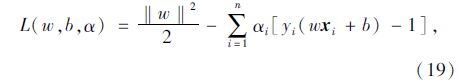
式中α,αi为拉格朗日系数,i=0,1,…,n。 通过求解可以得到一个x的分类式:
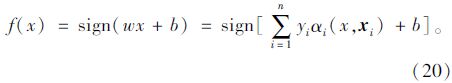
所谈到的分类都是2分类的情况,在N分类的情况下,主要有两种方式:一种是1 对多,另一种是1对1。前一种方法需要训练N个分类器,看第i个分类器是属于分类i还是属于分类i的补集(除去i的N-1个分类)。后一种方式需要训练N(N-1)/2个分类器,分类器(i,j)能够判断某个点是属于i还是属于j。1对1的方式优于1对多,故采用1对1的方式进行识别。本文采用林智仁教授提出的Libsvm进行分类[12],具体步骤如下:
(1) 按照Libsvm软件包的要求将训练样本转换为其要求格式。其中将170组数据做为训练集train.txt,建立其对应的标签样本为train_labels.txt,选择30组数据做为test.txt,建立起对应的标签为test_labels.txt。
(2) 将数据缩放。避免某些特征范围太大或太小,减少训练核函数内积时的数值计算困难问题。
(3) 选取适当的参数训练数据生成模型。调用Libsvm中的svmtrain进行训练,生成模型。
(4) 调入训练所得模型,对测试样本进行分类。利用上步所生成的model调用函数svmpredict对test.txt进行分类,得到对应的预测类型编码及分类正确率。采用相同的方法对Hu不变矩进行分类。
3 试验及分析 3.1 感兴趣区域预处理对于感兴趣区域的预处理包括图像增强和去噪两部分。交通标志图像库中的图像是在各种环境中采集的,当光照条件较差或者背光时,交通标志会模糊看不清楚,不利于识别。首先对感兴趣区域进行图像增强,采用直方图均衡化的增强方法。由于增强的图像普遍存在明显的噪音,中值滤波可以在去噪的同时保持较好的图像边缘细节,因此选择中值滤波进行去噪处理。
3.2 Zernike特征向量数据集的建立本文采用GTSRBT提供的识别图像和实时环境中采集的图像进行识别,选择常见的10种交通标志,如图 3所示。

|
| 图 3 十种待识别交通标志 Fig. 3 Ten traffic signs to be recognized |
对图 3的10类标志按顺序进行编码,每个编码对应的具体含义如表 2所示。
| 编码 | 1 | 2 | 3 | 4 | 5 |
| 含义 | 限速30 km/h | 限速100 km/h | 路口优先通行 | 无优先权 | 禁止通行 |
| 编码 | 6 | 7 | 8 | 9 | 10 |
| 含义 | 禁止驶入 | 危险警告 | 左转弯 | 右转弯 | 环岛行驶 |
其中选择每类交通标志在强光、阴暗、模糊、抖动、旋转、缩小等20种不同情况下的图像,每幅图像提取其7组Zernike矩(每幅图不止有7组Zernike矩,本文由试验得到7组有更好分类效果的Zernike矩),同时试验给出相同图像的7组Hu不变矩,由于篇幅有限,这里分别给出10种情况下限速100 km/h的Zernike矩和Hu矩,如表 3和表 4所示。
| 编码 | Zernike1 | Zernike2 | Zernike3 | Zernike4 | Zernike5 | Zernike6 | Zernike7 |
| 1 | 0.196 55 | 0.011 215 | 0.000 224 31 | 0.059 599 | 1.840 9 | 4.104 9 | 0.586 54 |
| 2 | 0.187 97 | 0.007 359 | 0.000 147 18 | 0.057 381 | 1.710 1 | 3.825 0 | 0.564 72 |
| 3 | 0.185 76 | 0.009 337 | 0.000 186 67 | 0.056 234 | 1.752 0 | 3.903 9 | 0.553 42 |
| 4 | 0.176 87 | 0.009 46 | 0.000 218 92 | 0.053 949 | 1.615 0 | 3.610 9 | 0.530 94 |
| 5 | 0.181 51 | 0.009 788 | 0.000 195 78 | 0.054 337 | 1.791 6 | 3.973 5 | 0.534 76 |
| 6 | 0.200 50 | 0.008 361 | 0.000 416 72 | 0.060 343 | 1.937 2 | 4.305 8 | 0.593 86 |
| 7 | 0.197 70 | 0.008 037 | 0.000 560 74 | 0.058 972 | 1.978 8 | 4.382 6 | 0.580 37 |
| 8 | 0.186 96 | 0.006 005 | 0.000 120 09 | 0.056 322 | 1.799 2 | 4.000 7 | 0.554 29 |
| 9 | 0.203 68 | 0.009 046 | 0.000 180 92 | 0.060 444 | 2.079 7 | 4.597 1 | 0.594 86 |
| 10 | 0.203 05 | 0.015 783 | 0.000 315 67 | 0.060 858 | 1.994 4 | 4.425 5 | 0.598 93 |
| 编码 | Hu1 | Hu2 | Hu3 | Hu4 | Hu5 | Hu6 | Hu7 |
| 1 | 5.039 1 | 15.543 5 | 18.710 9 | 21.307 6 | 43.223 8 | 29.685 4 | 41.446 3 |
| 2 | 6.520 6 | 17.954 8 | 22.752 4 | 24.887 7 | 49.282 1 | 34.060 1 | 49.407 7 |
| 3 | 6.336 9 | 18.651 3 | 23.647 1 | 26.630 4 | 54.631 0 | 37.884 2 | 52.119 4 |
| 4 | 5.789 5 | 16.728 5 | 19.043 1 | 22.804 2 | 44.662 6 | 31.364 0 | 43.846 3 |
| 5 | 6.673 8 | 19.208 8 | 24.908 5 | 27.122 7 | 56.365 1 | 37.205 6 | 53.295 4 |
| 6 | 5.976 4 | 15.679 7 | 21.363 0 | 24.087 8 | 47.141 4 | 31.960 2 | 47.830 7 |
| 7 | 6.700 5 | 17.030 0 | 21.554 1 | 24.039 2 | 47.043 0 | 32.793 1 | 48.046 4 |
| 8 | 6.365 6 | 17.969 6 | 21.480 0 | 26.419 9 | 50.668 1 | 35.690 1 | 51.281 7 |
| 9 | 6.384 3 | 17.617 5 | 21.429 6 | 28.111 2 | 54.314 5 | 37.154 3 | 53.053 2 |
| 10 | 6.203 3 | 17.163 1 | 22.737 2 | 24.686 1 | 49.419 2 | 33.795 7 | 48.499 9 |
按照上述方法对剩余的其他9种标志提取Zernike矩,得到试验所需的数据样本集,建立所需的featureData.txt。
3.3 试验结果通过试验分别采用Zernike不变矩和Hu不变矩对200幅图进行测试,将特征向量值分别输入SVM进行交通标志的识别,试验结果如表 5所示。
| 不变矩种类 | 样本种类 | 样本总数 | 训练集 | 测试集 | 识别率/% | 平均识别时间/ms |
| Zernike | 10 | 200 | 170 | 30 | 93.21 | 81.35 |
| Hu | 10 | 200 | 170 | 30 | 90.56 | 93.21 |
由表 5可知,采用Zernike矩特征向量与Hu矩特征向量分别作为SVM的输入进行识别,Zernike矩具有更高的识别率和更高的实时性。Zernike矩在试验过程中最少的识别时间为10.163 ms,平均识别时间在0.1 s以下,可以满足实时性的要求。
4 结论本文首先对感兴趣区域图像进行了预处理,以提高图像在阴暗、背光等条件下的图像识别效果,然后提取图像的Zernike矩特征值,建立了feature Data数据集,最后将特征值输入SVM进行训练得到识别模型,实现了测试集的识别。试验表明,该算法具有较高的识别率,同时可以满足实时性的要求,但是识别阶段训练前期的工作量较大,如何改进这部分的工作有待进一步研究。
| [1] | WEGMAN F. Implementing, Monitoring, Evaluating, and Updating a Road Safety Programme[C]//Europe 2003 Conference of the European Transport Safety Council:Targeted Road Safety Programmers in the EU. Brussels:SWOV Institute for Road Safety Research, 2003. |
| [2] | KHAN J F, BHUIYAN S M A,ADHAMI R R. Image Segmentation and Shape Analysis for Road-sign Detection[J]. |
| [3] | 冯春贵,祝诗平,王海军,等.基于改进模板匹配的限速标志识别方法研究[J].西南大学学报:自然科学版,2013, 35(4):167-172. FENG Chun-gui, ZHU Shi-ping, WANG Hai-jun, et al. On Identification of Speed-limit Signs Based on Modified Template Match[J]. Journal of Southwest University:Natural Science Edition,2013, 35(4):167-172. |
| [4] | 彭跃军.一种基于SURF的交通标志识别算法[J].信息技术, 2013(17):12-15. PENG Yue-jun. A Traffic Sign Recognition Algorithm Based on SURF[J]. Information Technology, 2013(17):12-15. |
| [5] | 胡锦成,李实英,李仁发.基于高稳定SURF特征的交通标志识别[J].计算机应用研究, 2012, 29(8):3179-3181. HU Jin-cheng, LI Shi-ying, LI Ren-fa. Traffic Sign Recognition Based on Stable SURFs[J]. Application Research of Computers, 2012, 29(8):3179-3181. |
| [6] | SHI M, WU H F, FLEYEH H. Support Vector Machines for Traffic Signs Recognition[C]//Proceedings of IEEE International Joint Conference on Neural Networks. Hong Kong:IEEE, 2008:516-524. |
| [7] | 江治国,李翔,陈小林. HU不变矩特征在道路交通标志识别系统中的应用[J].井冈山大学学报:自然科学版, 2013, 34(1):75-78. JING Zhi-guo, LI Xiang, CHEN Xiao-lin. Hu's Invariant Moments Using in Road Traffic Signs Recognition System[J].Journal of Jinggangshan University:Natural Science Edition, 2013, 34(1):75-78. |
| [8] | 田秋霞,刘成霞,杜晓.基于Zernike矩和BP网络的道路交通标志识别方法研究[J].浙江理工大学学报,2012, 29(2):235-239. TIAN Qiu-xia, LIU Cheng-xia, DU Xiao. Research on Method of Traffic Signs Recognition Based on Hu Invariant Moments and Zernike Invariant Moment[J]. Journal of Zhejiang Institute of Science and Technology, 2012, 29(2):235-239. |
| [9] | LIAO S X. PAWLAK M. On the Accuracy of Zernike Moments for Image Analysis[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1988, 20(12):1358-1364. |
| [10] | HU M K. Visual Pattern Recognition by Moment Invariants[J]. |
| [11] | VAPNIK V. An Overview of Statistical Learning Theory[J]. |
| [12] | CHANG C C, LIN C J. Libsvm:Alibrary for Support Vector Machines[J]. ACM Transaction on Intelligent Systems and Technology(TIST), 2011, 2(3):389-396. |
 2015, Vol. 31
2015, Vol. 31
