扩展功能
文章信息
- 王文博, 周继彪, 陈红, 游月省
- WANG Wen-bo, ZHOU Ji-biao, CHEN Hong, YOU Yue-sheng
- 基于VISSIM仿真的事故路段通行能力估算方法
- A Simulation Method for Capacity in Traffic Accident Section Based on VISSIM
- 公路交通科技, 2015, Vol. 31 (12): 120-127
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (12): 120-127
- 10.3969/j.issn.1002-0268.2015.12.020
-
文章历史
- 收稿日期: 2015-01-26
2. 中交第一公路勘察设计研究院有限公司, 陕西西安 710075;
3. 宁波工程学院交通学院, 浙江宁波 315211
2. CCCC First Highway Consultants Co., Ltd., Xi'an Shaanxi 710075, China;
3. School of Transportation, Ningbo University of Technology, Ningbo Zhejiang 315211, China
随着我国城市化进程的加速和机动车辆保有量的快速增长,城市快速路系统运输效益巨大,成为缓解城市交通拥堵的重要措施。一方面,城市快速路的形成将有力地支撑或推进城市空间结构的合理调整,从整体上提高城市交通的可达功能、快速功能和连通功能,以此满足城市内部中长距离机动车交通和对外交通的需求。另一方面,城市快速路的形成将紧密联系各功能核心组团的空间结构,支撑城市规模的合理扩展,带动周围地区土地的开发和利用。然而,快速路系统突发交通事故将严重影响城市交通的正常运行,并造成交通流紊乱,产生的交通波迅速地向上游传播且易发生交通拥挤阻塞现象,交通流密度达到临界值,导致其通行能力显著下降,行车延误和行程时间增加,甚至会造成一定的人员伤亡和财产损失,对区域路网交通运行环境和安全产生较大影响。因此,研究交通事故下城市快速路的通行能力有重要的意义。
近年来,城市化进程不断加快,城市快速路所承担的交通功能作用越来越显著,其运行安全性也越来越受到重视。目前,国内外学者对城市快速路的通行能力从不同角度进行了大量研究。国外方面对城市快速路通行能力的研究主要集中在快速路交织区长度、交织区几何构型、车道变换行为和交织区流量对通行能力的折减[1, 2]、基本路段通行能力[3, 4]和分、合流[5]对其通行能力的影响3大方面。TRB编写的道路通行能力手册(Highway Capacity Manual,HCM)2000年版和2010年版[6]对正常条件下城市快速路的通行能力也进行了详细阐述。在国内,李秀文等[7]针对城市快速路分、合流影响的通行能力进行了研究。钟连德等[8, 9]给出了理想通行能力的推荐值,并对快速路交织区的通行能力进行了仿真。张建勋等[10]利用VISSIM对地铁枢纽的客流进行了微观仿真。张菁等[11]在分析快速路交织区交通流特性的基础上,提出了改进的交通流模型。这些成果推动了快速路通行能力研究的发展,为城市快速路的规划、设计和进行服务水平分析提供了理论参考,但对因事故数据统计困难等原因造成的交通事故下快速路通行能力的研究并不深入,直接影响了交通事故的救援效率和应急响应措施。
鉴于此,笔者引入决策树ID算法,并结合车流波动理论,分析交通事故下城市快速路局部状态的演变过程和影响因素。以事故延迟时间为观测周期,运用VISSIM仿真软件,对事故路段的通行能力进行仿真模拟,以期为定量描述交通事故下快速路的通行能力交通特性并对其提供合理的交通管制措施、出行信息服务、交通组织诱导和应急救援等给出新的思路。
1 事故路段通行能力分析 1.1 影响因素分析道路通行能力是指在一定道路和交通条件下,道路上某点、某车道或某断面处可能通过的最大交通实体(车辆或行人)数,当有其他车辆混入时,均可采用当量标准车辆(小汽车)的等效通行能力为单位(pcu/h)来表示。区别于正常情况下的城市道路(考虑到正常条件下的通行能力影响因素),城市快速路事故路段通行能力的影响因素具有其特殊性,一般来说与事故点封闭车道数、行车道长度和宽度、事故路段限速、事故延迟时间等因素相关。
(1)事故点封闭车道数
事故发生后,出于安全和现场处理要求,所需空间有时需要关闭1条或多条车道,这将会大大降低城市道路路段的通行能力,导致交通拥挤、阻塞。
(2)车道长度与宽度
封闭的车道长度越长,驾驶员在该车道上的行驶速度和变换车道时的速度都会减少,这也会降低事故路段的通行能力。与正常情况下的城市道路通行能力修正一样,事故点允许行驶的车道宽度也会对事故段的通行能力有一定影响。
(3)事故路段限速
驾驶员在未封闭的车道上行驶时受到速度限制,提高了其通过的安全性和均衡车流速度,减少二次事故的发生,但其通行能力会降低。
(4)事故延迟时间
事故延迟时间与作业强度、事故类型、严重程度及交通条件等因素有关,且作业强度越强,事故延迟时间就越短,其通行能力恢复得也就越快。针对特殊事故路段的通行能力影响因素,例如隧道、桥梁等,除上述影响因素之外,还有其他特殊影响因素。隧道通行能力与照明强度、隧道入口交通标志等因素有关,而桥梁通行能力与坡度、线性等因素有关。
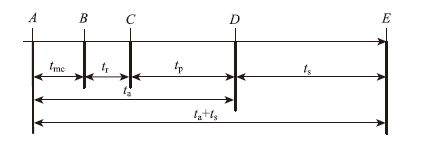
1.2 事故路段局部状态演变过程交通事故发生后,事故点路段的通行能力降低,当此处通行能力小于上游到达的交通量时,车辆会在事件点上游排队,并不断向上游延伸,甚至延伸到上游交叉口,当事故清理完毕后,道路通行能力渐渐恢复,拥挤车流开始消散。事故延迟时间和事故消散时间之和为拥挤持续时间,拥挤持续时间的组成部分如图 1所示。
|
| 图 1 拥挤持续时间 Fig. 1 Traffic congestion duration time tmc—事故监测与确认时间;tr—事故响应时间;tp—现场处理时间;ta—事故延迟时间;ts—消散时间;ta+ts—拥挤持续时间;A—事故开始状态;B—事故确认状态;C—警力到达状态;D—事故结束状态;E—拥挤结束状态 |
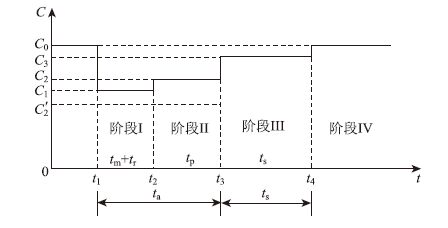
与事故拥挤持续时间相对应的道路局部状态演变过程分为4个阶段,即事件监测和响应阶段、现场事故处理阶段、拥挤影响持续阶段和交通初始状态恢复后阶段。C0(前)为事故前快速路路段通行能力;C0(后)为交通恢复后快速路路段通行能力;C1为警力到达前快速路路段通行能力;C2和C′2为现状处理条件下的快速路路段通行能力,表示通行能力可以增加或减小;C3为交通恢复条件下的快速路路段通行能力。城市快速路突发事故发生后的交通状态演变过程如图 2所示。
|
| 图 2 突发交通事故后交通状态演变过程 Fig. 2 Traffic state evolution process after sudden traffic incident t1—事故开始时间;t2—事故持续时间;t3—事故排除时间;t4—结束响应时间 |
(1)阶段I:事故监测与响应阶段
在突发交通事故造成局部车道临时关闭的情况下,事发车道的通行能力骤降为零,直至突发交通事件排除后才恢复。其间,事发车道车辆会变换车道至相邻车道上去,在一定范围内的车流处于紊流状态,车辆之间的相互影响比较大,因此,此时可通行车道的通行能力比其正常通行能力要小一些。其中,本阶段的t1时刻记为事故开始时间,t2时刻记为事故持续时间。
(2)阶段II:现场事故处理阶段
警力到达后,救援车辆、交通标志等设施相比事故发生时占有的空间要大,此时的通行能力比警力到达前的通行能力要小,即C2略小于C1;反之,此时的通行能力比警力到达前的通行能力要大,即C2略大于C1。为了简化分析阶段I和阶段II的通行能力,将C2等同于C1。其中,本阶段的t3时刻记为事故排除时间,t1至t2时刻间隔记为事故延迟时间。
(3)阶段III:拥挤影响持续阶段
事故结束后,由于事故结束前导致的拥挤车流还没完全消散,将经历拥挤影响持续,此时的通行能力受拥挤车流的交通构成、速度、车头间距等因素的影响,比正常情况下的通行能力要小,即C3略小于C0。其中,本阶段的t4时刻记为结束响应时间,t3至t4时刻间隔记为拥挤消散时间。
(4)阶段 IV:交通初始状态恢复后阶段
事故路段结束响应时间后,由于突发事故导致的拥挤车流完全消散,事故前快速路路段通行能力将恢复到C0状态。
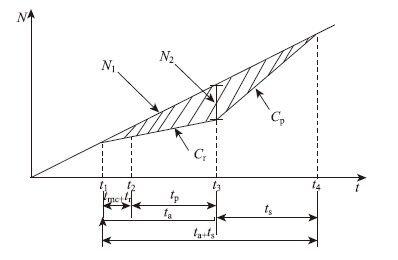
城市快速路事故路段交通拥挤过程从产生至消散的整个过程如图 3所示。
|
| 图 3 交通拥挤形成过程 Fig. 3 Traffic congestion formation process |
图 3中,横轴表示时间t,纵轴表示累计车辆数N。N1为累计到达车辆数;N2为最大排队车辆数;Cr为事故路段剩余通行能力;Cp为交通事故恢复后的道路的实际通行能力。
由图 3可知,估算的事故延迟时间和在该时间段通过的累计到达车辆数N1之间比值的倒数(斜率为Cr)为事故情况下的通行能力,通过计算公式得出的拥挤消散时间和在该时间段通过的累计车辆数之间比值的倒数(斜率为Cp)为状态恢复的通行能力(略大于道路实际的交通能力)。为了简化分析,本文只研究事故发生在城市快速路路段上的情形。
1.3 事故延迟时间和拥挤消散时间计算(1)事故延迟时间计算 考虑到不同交通事故类型下的城市快速路通行能力影响因素,其事故延迟时间也会有所不同。根据决策树ID算法的信息增益值对城市快速路不同事故类型下的延迟时间进行估算,其计算式如下:
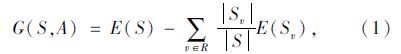

式中,S为样例的集合;E(S)为信息熵;Sv为S中A值为v的样例集合;P(ui)为类别i出现的概率;A为属性;R为属性A取值的集合;v为A的某一属性值;|Sv|和|S|为Sv和S中所含的样本数。
事故延迟时间是交通事件的发现时间、救援的到达时间和事件清除时间的总和。式(1)是两个信息量之间的差值,由期望信息和熵值可以得到对应的信息增益。选取某城市快速路的事故数作为样本,根据决策树ID算法[12],计算每个属性的信息增益,并选取具有最高增益的属性作为给定集合的测试属性,而并不考虑来自于根的路径。对被选取的测试属性创建一个节点,以该属性标记对该属性的每个值创建一个分支,并据此划分样本,从而确定交通事件的严重程度值,并根据该值判定事故延迟时间,如表 1所示。
| 事故类型 | 事故延迟时间/min |
| 抛锚(车辆不可移动) | 15 |
| 抛锚(车辆可移动) | 7 |
| 翻车(车辆类型为小汽车,无伤亡) | 33 |
| 翻车(车辆类型为小汽车,有伤亡) | 48 |
| 火烧(车辆类型为小汽车,无伤亡,无设施损坏) | 18 |
| 火烧(车辆类型为小汽车,无伤亡,有设施损坏) | 36 |
| 追尾(涉及车辆数≥3,车辆类型为小汽车、无伤亡) | 23 |
| 追尾(涉及车辆数≥3,车辆类型为小汽车、有伤亡) | 49 |
| 碰撞(有伤亡但无死亡,车辆类型为小汽车) | 37 |
| 碰撞(有伤亡但无死亡,车辆类型为大巴) | 59 |
(2)事故拥挤消散时间计算
事故拥挤消散时间通过车流波动理论求出,计算公式如式(3)~式(5)所示。
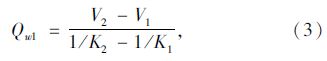
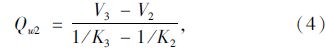
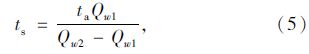
式中,Qw1为集结波的波流量;Qw2为消散波的波流量;Vi(i=1,2,3)为不同车流状态的车速;Ki(i=1,2,3)为不同车流状态的密度;ta为事故延迟时间;ts为事故拥挤消散时间。
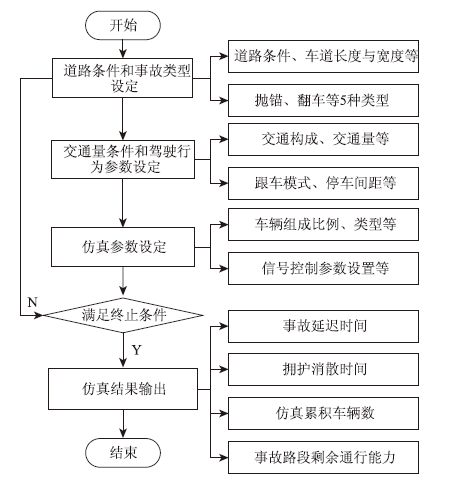
2 事故路段通行能力仿真建模 2.1 VISSIM仿真流程根据上述对城市快速路事故路段通行能力的理论分析,利用VISSIM5.1仿真软件对其事故情况下的通行能力进行仿真与估算,通过20次交通仿真,输出相对应的20组仿真结果,取其平均值以减少误差。城市快速路事故路段通行能力仿真分析流程如图 4所示。
|
| 图 4 交通仿真流程图 Fig. 4 Flowchart of traffic simulation |
(1)道路条件和事故类型设定
道路条件分为道路等级、行驶方向、是否有分隔带、双向车道数、车道宽度。事故类型分为抛锚、翻车、火烧、追尾、碰撞。文中以城市快速路基本路段为仿真背景,车道宽度设置为3.75 m,道路类型为城市快速路,单向车道数为3车道,仿真的道路长度为720.275 m,事故发生的车道位置距离起点360.826 m,以关闭左侧一条车道为例进行仿真试验。
(2)交通量条件设定
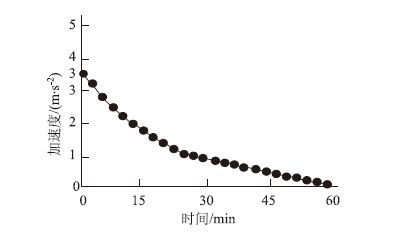
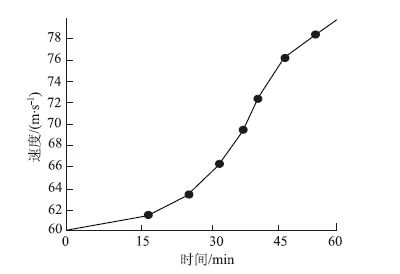
交通量条件包括交通构成、所占比例、交通量、速度等,小汽车的最大加速度分布函数如图 5所示,小汽车的期望速度分布如图 6所示。
|
| 图 5 小汽车最大加速度分布函数 Fig. 5 Maximum acceleration distribution function of car |
|
| 图 6 小汽车期望速度分布图 Fig. 6 Desired velocity distribution of car |
(3)驾驶行为参数设定
驾驶行为参数设置中,所在道路类型为城市快速路,前视距离最小值为0 m,最大值为 250 m,后视距离最小值为0 m,最大值为150 m,暂时走神的持续时间为0 s,持续概率为0,跟车模式采用Wiedemann 74模型,平均停车间距为2 m,安全距离的附加部分为2,安全距离的倍数部分为3。
2.3 仿真参数设定VISSIM5.1微观仿真软件并没有交通事故仿真模块,因此当事故发生后,文中通过对事故车道设置红灯等效的方法来进行交通事故仿真。事件发生时信号灯开始变红,持续到事故结束时变绿,事故车道的车辆将根据仿真软件中的驾驶决策行为进行换道行驶。VISSIM仿真相关参数设置如表 2和表 3所示。
| 车辆类型 | 小客车 | 公交车 | 货车 |
| 车辆组成比例/% | 84 | 3 | 13 |
| 参考折算系数 | 1 | 2 | 3 |
| 注:城市快速路仿真设置中,小客车含小货车,货车含大客车。 | |||
| 名称 | 红灯/黄灯 | 黄灯 | 红灯结束时间/s | 绿灯结束时间/s | 类型 | 周期 |
| 抛锚 | 0 | 0 | 1 080 | 2 400 | Cycle | 2 400 |
| 翻车 | 0 | 0 | 2 160 | 3 600 | Cycle | 3 600 |
| 火烧 | 0 | 0 | 1 260 | 2 400 | Cycle | 2 400 |
| 追尾 | 0 | 0 | 1 560 | 3 600 | Cycle | 3 600 |
| 碰撞 | 0 | 0 | 2 400 | 4 620 | Cycle | 4 620 |
以西安市南二环路为案例分析。南二环路道路等级为城市快速路,规划红线为100 m,主路双向6车道,辅路双向4条车道,车道宽度为3.75 m(VISSIM仿真时车道宽度和实际情况保持一致),设计车速为80 km/h。在城市快速路中,受到驾驶员自身驾驶特性的影响,其变换行为随意发生,行车过程中,驾驶员会根据本车速度、与前车的速度差(车速离散度)、与前车距离、相邻车道车辆车速车距等信息来决策是否可以进行车道变换操作。车辆在不同交通流状态下行驶时优先选择行驶车道,受车流状态变化影响进行车道变换。在城市快速路车流量较大的基本路段中,行车道过宽会导致车辆间的侧向净空加大,加大车辆穿插现象,三车道的道路条件出现4辆车并排行驶的现象,如图 7(a)所示。将会导致交通拥堵产生,且车辆行驶自由度降低,拥堵流难以消散,大大降低了道路通行能力。2013年3月30日(星期六),在南二环中段发生一起3辆车的追尾事故,如图 7(b)所示。事故类型为追尾(涉及车辆数≥3、车辆类型为小汽车、无伤亡)。根据现场实测,事故延迟时间为24.4 min,事故拥挤消散时间为19.5 min,事故路段通过的车辆数为52辆/min。

|
| 图 7 西安市南二环中段交通事故 Fig. 7 Traffic accident at middle section of South 2nd Ring Road in Xian |
在事故路段通行能力分析的基础上,基于VISSIM仿真流程,设定仿真条件(见3.2节)和仿真参数(见3.3节),通过对事故车道设置红灯等效的方法进行交通事故仿真。根据不同的事故类型选取相应的仿真时间,如表 3所示。通过分别改变交通仿真信号控制参数,对抛锚、翻车、火烧、追尾和碰撞5类事故类型进行了模拟仿真,基于上述仿真条件设定和仿真参数设置,输出仿真5种事故类型的仿真结果。
3.2 仿真结果分析根据上述仿真参数设置及车流波动模型,得到的仿真效果如图 8所示。

|
| 图 8 仿真3D效果图 Fig. 8 Simulation 3D rendering |
根据上述设定的仿真条件和设置的仿真参数,得到的仿真结果如表 4所示。
| 事故类型 | ta/min | ts/min | N1/ veh | N2/ pcu | Cr/(pcu·h-1) | n | Cs/(pcu·h-1) | β/% |
| 抛锚(车辆不可移动) | 15 | 3.5 | 732 | 944 | 3 776 | 3 | 1 800 | 69.926 |
| 翻车(车辆类型为小汽车,无伤亡) | 33 | 46.2 | 1 309 | 1 689 | 3 071 | 3 | 1 800 | 56.870 |
| 火烧(车辆类型为小汽车,无伤亡,无设施损坏) | 18 | 10 | 774 | 998 | 3 327 | 3 | 1 800 | 61.611 |
| 追尾(涉及车辆数≥3,车辆类型为小汽车,无伤亡) | 23 | 18.4 | 960 | 1 238 | 3 229 | 3 | 1 800 | 59.796 |
| 碰撞(有伤亡但无死亡,车辆类型为小汽车) | 37 | 51.7 | 1 290 | 1 664 | 2 698 | 3 | 1 800 | 49.963 |
| 注:ta—事故延迟时间;ts—拥挤消散时间;N1—仿真累积车辆数;N2—仿真累积标准车当量数;Cr—事故路段剩余通行能力;n—车道数;Cs—单车道通行能力;β—事故路段剩余通行能力的比例。 | ||||||||
由表 4可知,车辆抛锚的事故延迟时间与拥挤消散时间最小,事故路段剩余通行能力最大,事故路段剩余通行能力为3 776 pcu/h,其比例为69.926%;车辆起火、车辆追尾、车辆翻车的剩余通行能力为3 327,3 229,3 071 pcu/h,其比例分别为61.611%,59.796%,56.870%;车辆碰撞的事故延迟时间与拥挤消散时间最大,事故路段剩余通行能力最小,为2 698 pcu/h,其比例为49.963%。
3.3 仿真效果评价以案例中的追尾(涉及车辆数≥3,车辆类型为小汽车,无伤亡)事故为例进行仿真效果评价,其仿真结果的和实际结果的对比如表 5所示。
| 事故类型 | 追尾(涉及车辆数≥3,车辆类型为小汽车,无伤亡) | ||
| 参数 | 仿真结果 | 实际结果 | 相对误差/% |
| ta/min | 23.000 | 24.400 | -5.738 |
| ts/min | 18.400 | 19.500 | -5.641 |
| Cr/(pcu·h-1) | 3 229 | 3 120 | 3.494 |
| n | 3 | 3 | 0.000 |
| Cs /(pcu·h-1) | 1 800 | 1 800 | 0.000 |
| β / % | 59.796 | 57.778 | 3.494 |
| 注:表中各参数含义同表 4。 | |||
由表 5可以看出,微观交通仿真软件VISSIM能对事故路段通行能力进行仿真模拟,实际案例中的事故延迟时间和拥挤消散时间比仿真结果要大,相对误差分别为-5.738%和-5.641%;实际案例中的事故路段剩余通行能力为3 120 pcu/h,比仿真结果3 229 pcu/h小,相对误差为3.494%;实际案例中的事故路段剩余通行能力比例57.778%比仿真结果59.796%小,相对误差为3.494%;VISSIM仿真中的车道数和单车道通行能力和实际案例保持一致。
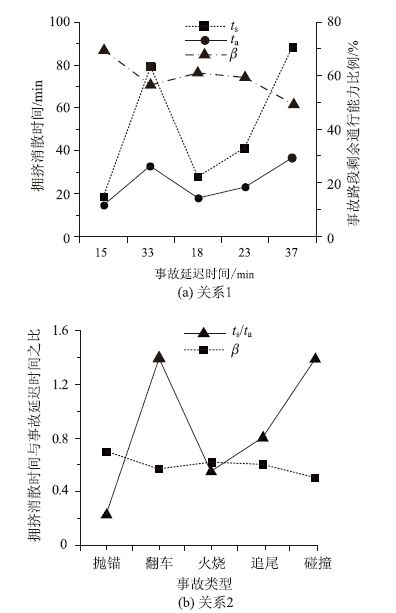
针对不同的事故类型,拥挤消散时间与事故延迟时间的变化趋势基本保持一致,其事故延迟时间和剩余通行能力会有很大不同,当事故类型为抛锚时,事故路段剩余通行能力比例β为69.926%;当事故类型为翻车时,β为56.870%;当事故类型为火烧时,β为61.611%;当事故类型为追尾时,β为59.796%;当事故类型为碰撞时,β为49.963%。拥挤消散时间与事故延迟时间之间的比值与事故路段的剩余通行能力比例有关,当拥挤消散时间ts与事故延迟时间ta的比值ts/ta为0.23时,剩余通行能力比例β为69.926%;当ts/ta为1.40时,β为56.870%;当ts/ta为0.56时,β为61.611%;当ts/ta为0.80时,β为59.796%;当ts/ta为1.40时,β为49.963%。事故路段剩余通行能力越大,其比值就越小,反之就越大。具体如图 9所示。
|
| 图 9 ts,ta,ts/ta与β的关系图 Fig. 9 Relationship of ts,t,ts/ta with β |
在用VISSIM对城市快速路交通流仿真模拟的过程中,通过分别改变交通仿真信号控制参数,对抛锚、翻车、火烧、追尾和碰撞5类事故类型进行了模拟仿真,微观交通仿真软件VISSIM能直观、翔实、具体地仿真出事故路段处交通流随时间变化的三维动画状态,直观和形象地模拟了城市快速路交通流的运行状况,避免了5种事故类型下无法直接观测事故路段通行能力的不足,为城市快速路中交通事故的救援效率和应急响应措施提供了一种新的视角和思路。
4 结论突发交通事故的应急与救援在城市交通管理中占有十分重要的地位,反映了城市的管理和应急保畅水平。通过对城市快速路事故路段通行能力进行微观仿真,得出以下结论:
(1)提出了基于VISSIM仿真的城市快速路事故路段通行能力的估算方法,该方法以求解事故延迟时间的决策树ID算法的信息增益值和求解拥挤消散时间的车流波动为理论基础。通过对事故后城市快速路通行能力的微观仿真与分析,得出的仿真结果与实际情况基本一致,表明该方法具有一定的理论指导意义和实用价值,可以为城市交通管理相关部门采取相应应对措施提供决策支持。
(2)通过交通事故下城市快速路通行能力衰减仿真结果可知,车辆抛锚条件下事故路段通行能力衰减最小,衰减比例为30.074%;车辆起火、车辆追尾和车辆翻车条件下通行能力衰减次之,衰减比例依次为38.389%,40.204%,43.130%;车辆碰撞条件下通行能力衰减最大,衰减比例为50.037%,可以利用交通诱导和对向车道通行对事故路段通行能力进行改善。
(3)对于不同的事故类型,其事故延迟时间和剩余通行能力会有很大不同,并且拥挤消散时间与事故延迟时间之间的比值与事故路段的剩余通行能力有关。事故路段剩余通行能力越大,其比值就越小,反之就越大。
(4)本文中只是针对追尾(涉及车辆数≥3,车辆类型为小汽车,无伤亡)事故进行了实例验证,但是由于现场事故路段数据统计比较困难,通过实例对其他4种事故类型(抛锚、翻车、火烧、碰撞)进行实例验证,尚需一步研究。
| [1] | LIU X M, LU S F. The Weaving Section Length Optimization Based on the Optimal Velocity Car-following Model and Symmetric Lane-changing Rule[J]. Applied Mechanics and Materials, 2013, 241-244:2064-2071. |
| [2] | YANG C, SHAO C, LIU L. Study on Capacity of Urban Expressway Weaving Segments[J]. Procedia-Social and Behavioral Sciences, 2012, 43(4):148-156. |
| [3] | THOMSON T, LIU X C, WANG Y, et al. Operational Performance and Speed-flow Relationships for Basic Managed Lane Segments[J]. Transportation Research Record, 2012, 2286:94-104. |
| [4] | ARON M, SEIDOWSKY R, COHEN S. Safety Impact of Using the Hard Shoulder during Congested Traffic:The Case of a Managed Lane Operation on a French Urban Motorway[J]. Transportation Research Part C:Emerging Technologies, 2013, 28(3):168-180. |
| [5] | WENG J, MENG Q. Modeling Speed-flow Relationship and Merging Behavior in Work Zone Merging Areas[J]. |
| [6] | Transportation Research Board. Highway Capacity Manual[M]. Washington, D.C.:TRB, 2010. |
| [7] | 李秀文,荣建,刘小明,等.快速路分、合流影响区交通特性及通行能力研究[J].公路交通科技, 2006, 23(1):101-104. LI Xiu-wen, RONG Jian, LIU Xiao-ming, et al. Analysis of Traffic Flow Characteristics and Capacities of Diverging and Merging Influence Areas[J].Journal of Highway and Transportation Research and Development, 2006, 23(1):101-104. |
| [8] | 钟连德,李秀文,荣建,等.城市快速路基本路段通行能力的确定[J].北京工业大学学报, 2006, 32(7):605-609. ZHONG Lian-de, LI Xiu-wen, RONG Jian, et al. Confirmation of the Capacity of Urban Expressway Basic Segment[J].Journal of Beijing University of Technology, 2006, 32(7):605-609. |
| [9] | 钟连德,荣建,孙小端,等.仿真求解快速路交织区通行能力[J].公路交通科技, 2006, 23(4):88-93. ZHONG Lian-de, RONG Jian, SUN Xiao-duan, et al. Capacity of Weaving Sections of Urban Expressway Obtained with Simulation Method[J]. Journal of Highway and Transportation Research and Development, 2006, 23(4):88-93. |
| [10] | 张建勋,韩宝明,李得伟. VISSIM在地铁枢纽客流微观仿真中的应用[J].计算机仿真, 2007, 24(6):239-242. ZHANG Jian-xun, HAN Bao-ming, LI De-wei. Application of VISSIM in Pedestrian Simulation of MTR Stations[J]. Computer Simulation, 2007, 24(6):239-242. |
| [11] | 张菁,巨永锋.快速路交织区交通流模型研究[J].中国公路学报, 2011, 24(5):89-93. ZHANG Jing, JU Yong-feng. Research on Traffic Flow Model of Expressway Weaving Area[J]. China Journal of Highway and Transport, 2011, 24(5):89-93. |
| [12] | 姬杨蓓蓓.交通事件持续时间预测方法研究[D].上海:同济大学, 2008. JIYANG Bei-bei. Forecast Method of Traffic Incident Duration[D]. Shanghai:Tongji University, 2008. |
 2015, Vol. 31
2015, Vol. 31
