扩展功能
文章信息
- 李爱增, 刘金阳, 李文权
- LI Ai-zeng, LIU Jin-yang, LI Wen-quan
- 信号交叉口下游车速离散特性
- Speed Dispersion Characteristics of Backward Section of Signalized Intersection
- 公路交通科技, 2015, Vol. 31 (12): 114-119,127
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (12): 114-119,127
- 10.3969/j.issn.1002-0268.2015.12.019
-
文章历史
- 收稿日期: 2014-09-09
2. 合肥工业大学交通运输工程学院, 安徽合肥 230009;
3. 东南大学交通学院, 江苏南京 210096
2. School of Transportation Engineering, Hefei University of Technology, Hefei Anhui 230009, China;
3. School of Transportation, Southeast University, Nanjing Jiangsu 210096, China
信号交叉口排队车辆绿灯期间驶向下游交叉口的过程中,由于车辆性能差异、路侧因素干扰等,车速开始逐渐离散。研究表明,车速离散对道路通行能力[1]、交通安全[2, 3, 4]、交通流稳定性[5]等具有重要影响。现有研究主要从平均速差[4, 6, 7]和车速标准差[2, 3]的角度对车速离散特性进行分析,研究对象一般是连续流设施,主要是高速公路[1]、城市快速路[5, 8]和普通公路[7, 9]。目前,对于间断流的车辆离散特性研究还较少。Bie等[10]研究了城市道路路段不同车道数情况下的车队离散特性,研究表明,随着车道数的增加,车队离散率降低。Bonneson等[11]考虑路段开口对车速离散的影响,对到达下游交叉口的流量进行了预测。魏明等[12, 13]考虑交叉口间不同的车速分布特征,从车速差异的角度探讨了上游交叉口排队车辆对下游交叉口的车辆到达的影响。本文的研究对象是间断流,主要 研究信号交叉口排队车辆绿灯启亮后驶向下游交叉口过程中的车速离散过程,分析车速的离散趋势及最终的离散位置,从而为城市道路线控及面控系统的设计、交通安全分析、通行能力研究、交通管理、流量预测、交通仿真等打下基础。
1 交通调查为了得到车速的离散过程和离散结果,选择相距较远的两交叉口之间的路段进行调查。本文选择平顶山市建设路与稻香路交叉口下游的建设路路段进行调查,调查路段总长1 300 m,调查路段内机非绿化带隔离,双向机动车隔离栏隔离,另外机非隔离带处有3个港湾式公交停靠站和3个绿化带开口。调查路段内共设置12个调查断面,考虑到公交车停靠站和机非隔离带开口等的影响,每隔100 m左右设置一个调查断面。调查时间为正常工作日周三的7:00—11:00,涵盖高峰和平峰两个时段。调查设备采用AxleLight RLU11便携式路侧激光交通调查仪。调查地点基本情况及调查设备布置如图 1所示,建设路与稻香路交叉口的信号配时状况如图 2所示。

|
| 图 1 调查地点及调查设备布置(单位: m) Fig. 1 Survey positions and layout of survey facilities (unit:m) |

|
| 图 2 信号配时图 Fig. 2 Signal timing diagram |
本文研究信号交叉口排队车辆驶离交叉口后的车速离散过程。根据排队车辆驶离交叉口后的运行特征,将调查数据中相邻车辆间车头时距大于20 s和小于0.5 s的样本剔除,最终得到各车道各断面的有效数据。各断面的平均车速计算式为:

式中,Vi为第i断面的平均车速;Vij为第i断面第j辆车的车速;N为第i断面的样本量。
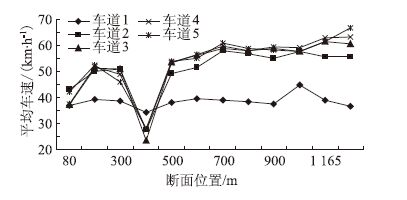
经计算得到各车道各断面高峰时段(7:30—8:30)的平均车速如图 3、表 1所示,平峰时段(9:30—10:30)的平均车速如图 4、表 2所示。
|
| 图 3 高峰时段车速变化状况 Fig. 3 Speed varying trends in peak period |
| 断面编号 | 断面位置/m | 平均车速/(km⋅h-1) | ||||
| 车道1 | 车道2 | 车道3 | 车道4 | 车道5 | ||
| 1 | 80 | 36.91 | 43.06 | 37.35 | 37.68 | 42.14 |
| 2 | 220 | 39.33 | 50.26 | 51.26 | 51.91 | 52.31 |
| 3 | 300 | 38.68 | 51.13 | 50.98 | 48.92 | 46.13 |
| 4 | 385 | 34.24 | 27.64 | 23.38 | 27.60 | 28.26 |
| 5 | 500 | 38.18 | 49.27 | 53.73 | 53.27 | 53.86 |
| 6 | 600 | 39.51 | 51.46 | 56.16 | 56.55 | 55.00 |
| 7 | 700 | 39.08 | 57.88 | 58.98 | 59.64 | 60.87 |
| 8 | 800 | 38.45 | 56.77 | 57.95 | 57.88 | 58.87 |
| 9 | 900 | 37.64 | 55.09 | 58.92 | 59.55 | 58.35 |
| 10 | 1 000 | 44.79 | 57.64 | 57.68 | 59.22 | 57.65 |
| 11 | 1 165 | 39.01 | 55.63 | 61.66 | 63.03 | 61.40 |
| 12 | 1 265 | 36.81 | 55.62 | 60.63 | 63.35 | 66.80 |
| 断面编号 | 断面位置/m | 平均车速/(km⋅h-1) | ||||
| 车道1 | 车道2 | 车道3 | 车道4 | 车道5 | ||
| 1 | 80 | 34.90 | 42.75 | 44.37 | 45.52 | 45.78 |
| 2 | 220 | 37.35 | 50.48 | 52.91 | 52.76 | 53.58 |
| 3 | 300 | 35.46 | 49.05 | 49.66 | 47.95 | 45.06 |
| 4 | 385 | 32.57 | 48.26 | 23.66 | 26.83 | 32.61 |
| 5 | 500 | 36.75 | 51.09 | 54.03 | 54.48 | 52.76 |
| 6 | 600 | 38.98 | 53.28 | 56.88 | 58.38 | 61.63 |
| 7 | 700 | 39.99 | 57.62 | 59.99 | 60.64 | 60.39 |
| 8 | 800 | 39.86 | 58.48 | 58.22 | 59.53 | 58.24 |
| 9 | 900 | 37.64 | 56.85 | 57.60 | 58.9 | 56.83 |
| 10 | 1 000 | 48.64 | 58.67 | 58.57 | 59.05 | 57.91 |
| 11 | 1 165 | 40.00 | 57.55 | 62.03 | 64.19 | 64.15 |
| 12 | 1 265 | 40.06 | 56.09 | 59.65 | 63.25 | 63.32 |
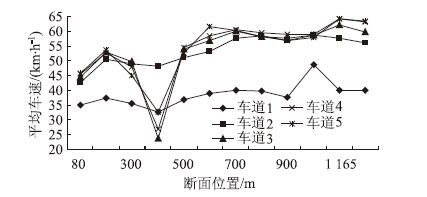
|
| 图 4 平峰时段车速变化状况 Fig. 4 Speed varying trends in off peak period |
可以看出,随着车辆向交叉口下游移动,总体来说,车速逐渐增加,车辆逐渐离散。但在第4断面即385 m处,第2至第4车道的车速出现了明显的降低,其原因主要是第4断面下游紧邻一公交停靠站,该公交停靠站对面为中央花园小区,下车乘客有一大部分横穿建设路至中央花园小区,影响了路段车辆的正常行驶。
为了分析信号交叉口排队车辆驶离交叉口后的正常离散过程,取高峰和平峰时段第3、第5断面的车速平均值作为第4断面的车速进行路段车辆的正常离散过程分析。调整后的第4断面车速值如表 3所示。
| 时段 | 断面位置/m | 平均车速/(km⋅h-1) | ||||
| 车道1 | 车道2 | 车道3 | 车道4 | 车道5 | ||
| 高峰 | 385 | 34.24 | 50.20 | 52.36 | 51.10 | 50.00 |
| 平峰 | 385 | 32.57 | 50.07 | 51.85 | 51.22 | 48.91 |
为了得到各车道高峰和平峰时段车速随距离的变化特征,利用线性函数、二次函数、复合函数、生长函数、对数函数、三次函数、S形曲线、指数函数、逆函数、幂函数和逻辑函数对各车道车速与距离的关系进行回归分析。
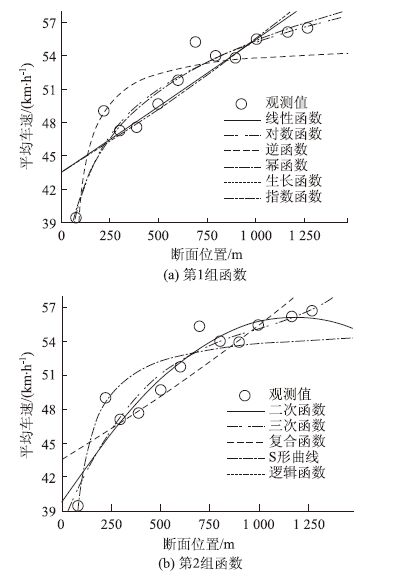
以第2车道为例,高峰时段的回归分析结果如表 4和图 5所示。
|
| 图 5 高峰时段第2车道车速回归分析图 Fig. 5 Regression analysis diagram of speed on the 2nd lane in peak period 注:(a)中,生长函数与指数函数重合;(b)中,复合函数与逻辑函数重合。 |
| 方程 | 模型概述 | 参数估计 | |||||||
| R2 | F | d1 | d2 | S | b0 | b1 | b2 | b3 | |
| 线性函数 | 0.658 | 19.214 | 1 | 10 | 0.001 | 46.648 | 0.009 | ||
| 对数函数 | 0.793 | 38.270 | 1 | 10 | 0.000 | 22.396 | 4.858 | ||
| 逆函数 | 0.699 | 23.234 | 1 | 10 | 0.001 | 55.925 | -1 121.046 | ||
| 二次函数 | 0.798 | 17.815 | 2 | 9 | 0.001 | 42.449 | 0.027 | -1.285E-5 | |
| 三次函数 | 0.799 | 10.619 | 3 | 8 | 0.004 | 42.926 | 0.023 | -6.183E-6 | -3.285E-9 |
| 复合函数 | 0.651 | 18.666 | 1 | 10 | 0.002 | 46.660 | 1.000 | ||
| 幂函数 | 0.808 | 41.963 | 1 | 10 | 0.000 | 28.796 | 0.096 | ||
| S形曲线 | 0.739 | 28.282 | 1 | 10 | 0.000 | 4.026 | -22.644 | ||
| 生长函数 | 0.651 | 18.666 | 1 | 10 | 0.002 | 3.843 | 0.000 | ||
| 指数函数 | 0.651 | 18.666 | 1 | 10 | 0.002 | 46.660 | 0.000 | ||
| 逻辑函数 | 0.651 | 18.666 | 1 | 10 | 0.002 | 0.021 | 1.000 | ||
| 注:R2 为判定系数;F为F检验值;d1,d2为自由度;S 为F检验值的实际显著性水平;b0为表示常数项;b1,b2,b3为回归参数。 | |||||||||
综合考虑这11种回归曲线的判定系数R2值和应用的便利性,选择三次函数对第2车道高峰时段车速与距离的关系进行描述:
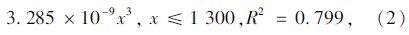
式中,y为平均车速;x为断面距离。 第2车道平峰时段的回归分析结果如表 5和图 6所示。
| 方程 | 模型概述 | 参数估计 | |||||||
| R2 | F | d1 | d2 | S | b0 | b1 | b2 | b3 | |
| 线性函数 | 0.735 | 27.781 | 1 | 10 | 0 | 46.174 | 0.011 | ||
| 对数函数 | 0.868 | 66.036 | 1 | 10 | 0 | 17.827 | 5.693 | ||
| 逆函数 | 0.727 | 26.603 | 1 | 10 | 0 | 57.027 | -1 279.901 | ||
| 二次函数 | 0.903 | 41.976 | 2 | 9 | 0 | 41.037 | 0.032 | -1.572E-5 | |
| 三次函数 | 0.911 | 27.141 | 3 | 8 | 0 | 42.532 | 0.021 | 5.170E-6 | -1.030E-8 |
| 复合函数 | 0.724 | 26.293 | 1 | 10 | 0 | 46.238 | 1.000 | ||
| 幂函数 | 0.882 | 74.719 | 1 | 10 | 0 | 26.433 | 0.112 | ||
| S形曲线 | 0.768 | 33.097 | 1 | 10 | 0 | 4.046 | -25.655 | ||
| 生长函数 | 0.724 | 26.293 | 1 | 10 | 0 | 3.834 | 0 | ||
| 指数函数 | 0.724 | 26.293 | 1 | 10 | 0 | 46.238 | 0 | ||
| 逻辑函数 | 0.724 | 26.293 | 1 | 10 | 0 | 0.022 | 1.000 | ||
| 注:表中符号意义同前。 | |||||||||
|
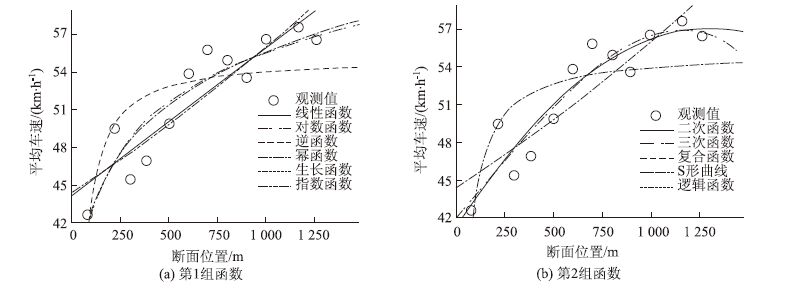
| 图 6 平峰时段第2车道车速回归分析图 Fig. 6 Regression analysis diagram of speed on the 2nd lane in off peak period 注:(a)中,生长函数与指数函数重合;(b)中,复合函数与逻辑函数重合。 |
综合考虑这11种回归曲线的判定系数R2和应用的便利性,选择三次函数对第2车道平峰时段车速与距离的关系进行描述:
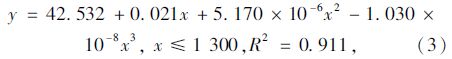
式中各变量意义同前。
同理,对其他车道高峰和平峰时段车速与距离的关系进行回归分析,综合考虑各回归曲线的判定系数R2和应用的便利性,得到回归分析结果如表 6所示。
由表 6可知,最外侧的第1车道由于受到路侧公交停靠站及机非隔离带开口的影响,车速的离散过程受到了较大的干扰,车速并未随距离表现出较好的相关性。除了第1车道外,各车道车速与距离具有较好的相关性。
| 车道编号 | 时段 | 模型 | R2 | 距离范围/m |
| 1 | 高峰 | y=39.489-0.019x+4.292×10-5x2-2.299×10-8x3 | 0.261 | x≤1 300 |
| 平峰 | y=37.845-0.027x+6.556×10-5x2-3.399×10-8x3 | 0.555 | x≤1300 | |
| 2 | 高峰 | y=42.926+0.023x-6.183×10-6x2-3.285×10-9x3 | 0.799 | x≤1 300 |
| 平峰 | y=42.532+0.021x+5.170×10-6x2-1.030×10-8x3 | 0.911 | x≤1 300 | |
| 3 | 高峰 | y=5.172+7.921lnx | 0.939 | x≤1 300 |
| 平峰 | y=42.528+0.037x-2.770×10-5x2+7.603×10-9x3 | 0.887 | x≤1 300 | |
| 4 | 高峰 | y=0.779+8.681lnx | 0.940 | x≤1 300 |
| 平峰 | y=43.431+0.031x-1.673×10-5x2+4.010×10-9x3 | 0.884 | x≤1 300 | |
| 5 | 高峰 | y=38.745+0.052x-5.373×10-5x2+2.313×10-8x3 | 0.866 | x≤1 300 |
| 平峰 | y=43.623+0.026x-1.2×10-5x2+2.44×10-9x3 | 0.726 | x≤1 300 |
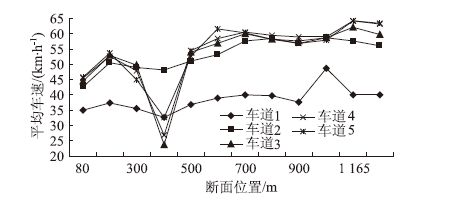
高峰和平峰时段,5个车道同一断面的车速平均值如表 7及图 7所示。
| 断面位置/m | 80 | 220 | 300 | 385 | 500 | 600 | 700 | 800 | 900 | 1 000 | 1 165 | 1 265 |
| 高峰时段 | 39.428 | 49.014 | 47.168 | 47.577 | 49.662 | 51.736 | 55.29 | 53.984 | 53.91 | 55.396 | 56.146 | 56.642 |
| 平峰时段 | 42.664 | 49.416 | 45.436 | 46.922 | 49.822 | 53.83 | 55.726 | 54.866 | 53.564 | 56.568 | 57.584 | 56.474 |
|
| 图 7 车速平均值变化状况 Fig. 7 Varying trends of average speed |
利用上述相同的分析方法可以得到高峰和平峰时段各车道同一断面车速平均值与距离的回归关系方程:
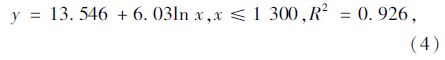
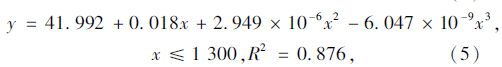
式中各变量意义同前。
由上述分析可知,随着车辆向交叉口下游移动,总体来说,车速逐渐增加,车辆逐渐离散,车速在700 m左右基本趋于稳定,车辆离散过程基本结束。另外,可以看出,平峰时段车速略高于高峰时段,在完全离散后平峰和高峰时段的车速基本相等。
5 实例验证为了对回归方程进行验证,选择建设路与稻香路交叉口下游路段不同调查日(星期四)的调查数据进行分析,调查得到的12个断面的车速平均值如表 8所示。按式(4)、式(5)计算得到的各断面高峰和平峰时段的车速值以及高峰、平峰时段车速调查值和计算值之间的相对误差如表 8所示。
| 断面位置/m | 80 | 220 | 300 | 385 | 500 | 600 | 700 | 800 | 900 | 1 000 | 1 165 | 1 265 |
| 高峰调查值/(km⋅h-1) | 39.134 | 49.581 | 46.993 | 48.575 | 50.157 | 52.196 | 56.761 | 55.226 | 56.799 | 56.567 | 57.907 | 57.341 |
| 高峰计算值/(km⋅h-1) | 39.970 | 46.070 | 47.940 | 49.444 | 51.020 | 52.119 | 53.049 | 53.854 | 54.564 | 55.200 | 56.121 | 56.617 |
| 相对误差/% | 2.136 | 7.081 | 2.015 | 1.789 | 1.721 | 0.148 | 6.540 | 2.484 | 3.935 | 2.417 | 3.084 | 1.263 |
| 平峰调查值/(km⋅h-1) | 43.321 | 49.231 | 44.854 | 47.37 | 49.886 | 53.846 | 56.501 | 54.601 | 54.61 | 57.419 | 56.903 | 56.714 |
| 平峰计算值/(km⋅h-1) | 43.448 | 46.030 | 47.494 | 49.014 | 50.973 | 52.547 | 53.963 | 55.183 | 56.172 | 56.894 | 57.403 | 57.240 |
| 相对误差/% | 0.293 | 6.502 | 5.886 | 3.471 | 2.179 | 2.412 | 4.492 | 1.066 | 2.860 | 0.914 | 0.879 | 0.927 |
可以看出,高峰和平峰时段车速调查值与计算值之间的相对误差都在8%以内,回归方程具有较好的计算精度。
6 结论采用路侧激光交通调查设备对信号交叉口下游1 300 m 路段内12个断面的车速进行调查,得到了高峰和平峰时段的车速值。然后从车速与距离关系的角度对信号交叉口下游的车辆离散特性进行研究,得到如下结论。
(1)采用11种回归曲线对各车道高峰和平峰时段车速与距离的关系进行回归分析,得到了相应的回归方程。结果表明,除第1车道外,各车道车速与距离具有较好的相关性。
(2)采用回归分析方法得到高峰和平峰时段各车道同一断面车速平均值与距离的回归关系模型。回归分析表明,各车道同一断面车速平均值与距离具有较强的相关性。
(3)高峰和平峰时段车速在距离上游交叉口700 m 左右趋于离散。另外,平峰时段车速略高于高峰时段,700 m之后高峰和平峰时段的车速基本相等。
(4)路段行人横穿马路对车速离散特性有较大影响,路侧公交停靠站及机非隔离带开口也会对外侧车道的车辆离散特性产生影响。另外,本文主要是针对四相位信号交叉口下游的车速离散特性进行分析,对于其他条件下交叉口下游的车速离散特性进行分析也是下一步研究的重点。
| [1] | 王昊,王炜,陈竣.车速离散性对高速公路实际通行能力的影响[J].北京工业大学学报, 2010, 36(10):1389-1395. WANG Hao, WANG Wei, CHEN Jun. Effects of Speed Dispersion on Capacity of Freeways[J]. Journal of Beijing University of Technology, 2010, 36(10):1389-1395. |
| [2] | 裴玉龙,程国柱.高速公路车速离散性与交通事故的关系及车速管理研究[J].中国公路学报, 2004, 17(1):74-78. PEI Yu-long, CHENG Guo-zhu. Research on the Relationship between Discrete Character of Speed and Traffic Accident and Speed Management of Freeway[J]. China Journal of Highway and Transport, 2004, 17(1):74-78. |
| [3] | 吴义虎,武志平.基于平均车速和车速标准差的路段安全分析方法[J].公路交通科技, 2008, 25(3):139-142. WU Yi-hu, WU Zhi-ping. A Safety Analysis Method for Highway Based on Average Speed and Speed Standard Deviation[J]. Journal of Highway and Transportation Research and Development, 2008, 25(3):139-142. |
| [4] | 芦方强.高速公路车速离散性对交通安全的影响研究[D].南京:东南大学, 2007. LU Fang-qiang. Research on Speed Dispersion's Influence on Traffic Safety on Freeway[D]. Nanjing:Southeast University, 2007. |
| [5] | 王昊,王炜,陈峻.车速离散对稠密交通流稳态流量的影响[J].吉林大学学报:工学版, 2009, 39(增1):109-114. WANG Hao, WANG Wei, CHEN Jun. Effects of Speed Difference on Steady Flow of Dense Traffic[J]. Journal of Jilin University:Engineering and Technology Edition, 2009, 39(S1):109-114. |
| [6] | 王昊,王炜,陆建,等.基于跟驰理论的车速离散度定义及特性[J].东南大学学报:自然科学版, 2009, 39(1):161-165. WANG Hao, WANG Wei, LU Jian, et al. Car-following Theory Based Speed Dispersion Definition and Related Properties[J]. Journal of Southeast University:Natural Science Edition, 2009, 39(1):161-165. |
| [7] | 陈伟伟.公路车速离散性对交通安全作用影响研究[D].南京:东南大学, 2010. CHEN Wei-wei. Research on Speed Dispersion Effect on Highway's Traffic Safety[D]. Nanjing:Southeast University, 2010. |
| [8] | WANG H, WANG W, CHEN X, et al. Experimental Features and Characteristics of Speed Dispersion in Urban Freeway Traffic[J]. |
| [9] | 吕贞.普通公路车速离散性与交通流微观特性关系研究[D].南京:东南大学, 2010. LV Zhen. Research on Relationship between the Speed Difference and the Micro-traffic Flow on Highway[D]. Nanjing:Southeast University, 2010. |
| [10] | BIE Y M, LIU Z Y, MA D F, et al. Calibration of Platoon Dispersion Parameter Considering the Impact of the Number of Lanes[J]. |
| [11] | BONNESON J A, PRATT M P, VANDEHEY M A. Predicting Arrival Flow Profiles and Platoon Dispersion for Urban Street Segments[J]. |
| [12] | 魏明,孙博.一种车速对数正态分布的车队离散模型[J].北京工业大学学报, 2013, 39(10):1521-1525. WEI Ming, SUN Bo. A Platoon Dispersion Model Based on Lognormal Distribution of Speed[J]. Journal of Beijing University of Technology, 2013, 39(10):1521-1525. |
| [13] | 魏明,陈学武,孙博.一种车速截断对数正态分布的车队离散模型[J].东南大学学报:自然科学版, 2013, 43(4):885-889. WEI Ming, CHEN Xue-wu, SUN Bo. Platoon Dispersion Model Based on Truncated Lognormal Distribution of Speed[J]. Journal of Southeast University:Natural Science Edition, 2013, 43(4):885-889. |
 2015, Vol. 31
2015, Vol. 31
