公路交通科技  2015, Vol. 31 Issue (12): 94-99,107

扩展功能

文章信息

彭建新, 蔡明文, 张建仁, 胡守旺, 刘扬
PENG Jian-xin, CAI Ming-wen, ZHANG Jian-ren, HU Shou-wang, LIU Yang
基于线性增量的混凝土表面氯离子浓度预测模型
A Prediction Model for Concrete Surface Chloride Ion Concentration Based on Linear Increment
公路交通科技, 2015, Vol. 31 (12): 94-99,107
Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (12): 94-99,107
10.3969/j.issn.1002-0268.2015.12.016

文章历史

收稿日期: 2014-09-22
引用本文 0
彭建新, 蔡明文, 张建仁, 胡守旺, 刘扬. 基于线性增量的混凝土表面氯离子浓度预测模型[J]. 公路交通科技, 2015, Vol. 31 (12): 94-99,107.
PENG Jian-xin, CAI Ming-wen, ZHANG Jian-ren, HU Shou-wang, LIU Yang. A Prediction Model for Concrete Surface Chloride Ion Concentration Based on Linear Increment[J]. Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (12): 94-99,107.
基于线性增量的混凝土表面氯离子浓度预测模型
彭建新, 蔡明文, 张建仁, 胡守旺, 刘扬    
长沙理工大学土木与建筑学院, 湖南长沙 410114
收稿日期: 2014-09-22
基金项目: 国家重点基础研究发展计划项目(九七三计划)(2015CB057701);国家自然科学基金项目(51178060,51378081);交通运输部主干学科应用基础研究项目(2014319825160);湖南省教育厅优秀青年项目(15B015); 湖南省研究生创新省级项目(CX2015B344)..
作者简介: 彭建新(1978-),男,江西安福人,副教授,博士.
摘要: 基于Fick第二扩散定律,综合考虑了混凝土初始表面氯离子浓度以线性方式变化、扩散系数随时间不断减小以及温湿度对氯离子扩散的影响,把氯离子扩散过程分为两个阶段,推导得到一个新的氯离子扩散方程,结合现有数据,对理论数学模型进行了验证。结果表明:随着表面氯离子浓度以线性积累速率的减慢,短期内氯离子扩散过程也变得缓慢;阶段一与阶段二时间结合点处的两个氯离子曲线分布得到很好的吻合,用新方程所得到的氯离子分布曲线与以往普遍采用基准方程得到的分布曲线也能很好地匹配,在分别计算10 a,25 a,50 a混凝土中钢筋表面氯离子浓度到达锈蚀临界浓度时,用新方程比采用基准方程时要提前约3%~14%,且随着时间的增长二者之间差异不断减小。
关键词: 桥梁工程     混凝土     线性增量     扩散方程     表面氯离子浓度    
A Prediction Model for Concrete Surface Chloride Ion Concentration Based on Linear Increment
PENG Jian-xin , CAI Ming-wen, ZHANG Jian-ren, HU Shou-wang, LIU Yang     
School of Civil Engineering and Architecture, Changsha University of Science and Technology, Changsha, Hunan 410114
Abstract: Based on the Fick's second law of diffusion, we divided the chloride ion diffusion process into 2 stages when taking an overall consideration to the influence of variation of chloride concentration in initial surface of concrete in a linear way, decrease of diffusion coefficient with time and temperature and humidity on chloride ion diffusion. On this basis, a new chloride ion diffusion equation is derived. Combing with the existing data, the theoretical model is verified. The result shows that (1) as the linear accumulation rate of the chloride ion concentration in the surface slows down, the chloride ion diffusion process also becomes slowly in the short term; (2) the distributions of the 2 chloride curves at the combining point of stage one and stage two is well fit, and chloride ion distribution curve obtained by the new equation is well matched with the previous one obtained by widely used benchmark equation; (3) when the calculating result of chloride ion concentration on reinforcement surface in concrete of 10, 25 and 50 years tending to critical concentration of reinforcement corrosion, adopting the new equation is about 3%-14% in advance compared to adopting the benchmark equation, and the difference between them decreases as time goes.
Key words: bridge engineering     concrete     linear increment     diffusion equation     surface chloride ion concentration    
 0 引言

混凝土结构在氯盐环境下，氯离子能够渗入混凝土，当钢筋表面氯离子浓度超过临界值时能够引起混凝土内钢筋锈蚀。这种锈蚀会减少钢筋截面积进而降低结构承载能力,而且钢筋锈蚀产物会引起混凝土开裂甚至剥落。混凝土结构在氯盐环境下的使用寿命取决于混凝土的氯离子扩散渗透性能，而氯离子渗透可用Fick第二扩散定律描述，并得到一个在一定初始条件和边界条件下的数学解。但是，它有严格的条件限制：混凝土是均匀的半无限介质,氯离子扩散系数必须恒定,氯离子不与混凝土发生反应。长期的氯离子扩散过程不能直接用短期测试结果确定。短期测试结果仅仅在测试时间范围内有效，把短期测试结果推断到长期过程中去是十分必要的。

目前，诸多国内外学者研究混凝土构件在氯盐环境下氯离子扩散系数时变性规律[1]、桥梁结构剩余使用寿命预测方法[2]。有学者探讨了混凝土结构在应力、水灰比等多因素作用下的氯离子扩散方程[3, 4, 5]、氯离子扩散系数原位测量研究[6]。但是考虑初始氯离子浓度和扩散系数的变化对氯离子扩散方程的影响，把扩散过程分两个阶段来研究的相关报道尚未见。

本文首先利用Fick第二扩散定律，推导了考虑混凝土表面氯离子浓度随时间以线性方式增加、氯离子扩散系数不断减小的氯离子扩散方程，并得到此条件下的基准数学解。结合模拟人工气候环境下氯盐喷雾试验结果，对氯离子扩散方程基准数学解进行了较好的验证，并与以往普遍采用基准氯离子扩散方程作分析验证。

1 氯离子扩散新方程及数学解

混凝土中氯离子扩散过程可以通过Fick第二扩散定律建立的模型描述，但它采用了以下假设[7, 8]：混凝土是半无限均匀介质。氯离子扩散时不与混凝土结合。氯离子扩散系数是一个恒定值，为：

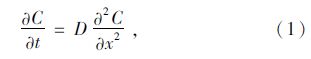
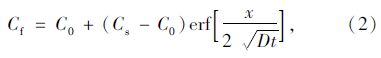
式中，t为时间；D为混凝土中氯离子扩散系数；x为距混凝土表面的距离；C为距混凝土表面x处的氯离子浓度(混凝土质量%)。满足初始条件：当t=0，x>0时，C=C0 ；满足边界条件：当x=0，t>0时，C=Cs。式(1)的数学解为：
式中erf为补偿误差函数。

在多数情况下，混凝土表面携带了一定浓度的氯离子。因此，Crank[9]提供了式(2)的数学表达式为：

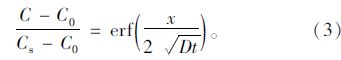
此外，由Andrade[10]，Ann[11]，Meira[12]等人对受到干湿循环或冲洗过程的混凝土的研究指出，混凝土表面最外层氯离子的分布不遵循式(3)，它比预期的浓度要低，这是因为混凝土表面存在一个对流区Δx，考虑对流区时，用x-Δx代替x。式(2)、(3)只适用于氯离子扩散系数趋于恒定值的情况。Tang和Nilsson[13]，Stanish和Thomas[14]等指出混凝土中扩散系数随着时间推移急剧下降，与时间的关系为：

式中，Da为ta时刻混凝土的氯离子扩散系数；Dr为水化时期tr时刻的氯离子扩散系数；m为时间因数，为一个常数，文献[15]取0.64。

Page与Tarras[16]等研究指出温度、湿度对氯离子扩散系数的影响分别为：

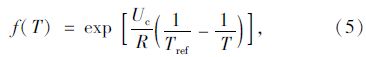
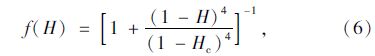
式中，T为当前温度；Tref为参考温度,Tref=296 K；R为气体常数8.34 J/(mol·K)；Uc为氯离子扩散过程的活化能。普通硅酸盐混凝土的活化能，当水灰比为0.4时，Uc取41.8±4.0；当水灰比为0.5时，Uc取44.6±4.3。
式中，H和Hc分别为当前湿度和临界湿度Hc=0.75。

考虑温度、湿度对氯离子扩散系数的影响，利用式(5)、(6)对式(4)进行修正，得到：

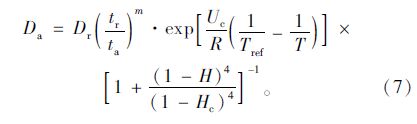
在多数情况下，初始表面氯离子浓度不是一个恒定值，它有一个积累过程。表面氯离子积累周期的长短很大程度依赖于所暴露的环境，较长周期主要是除冰盐环境，较短周期主要是海水、浪溅等环境。第一种积累过程是基于Mustafa和Yusof[17]，Costa和Appleton[18]，Meira等[12]数据建立的，它呈线性方式积累，主要是对通过空气介质传播氯离子的混凝土。第二种积累过程是基于Costa和Appleton[19],Kato等[20]，Shin和Kim[21]等数据建立的，它以平方根方式积累，主要针对混凝土暴露在干湿循环中的情况。本文主要考虑除冰盐环境，混凝土表面氯离子浓度以线性积累，为：

式中k为常量。

当满足初始氯离子浓度为0、表面氯离子浓度以线性方式增加、氯离子扩散系数是一个恒定值的条件时，氯离子的扩散过程可以采用以下Grank[3]提供的数学表达式为：

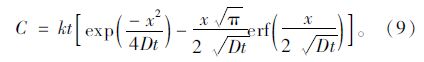
初始暴露时期(阶段1)，Cs和Da都是随时间变化的，扩散系数Da满足式(4)。此条件下，式(3)和式(9)都不适用于这种氯离子扩散模型。随后时期(阶段2)Cs和Da都趋于一个恒定值，式(3)适用于这个阶段。此外，以上两个扩散阶段是在不同的条件下进行的，有不同的数学表达式。因此，需要一个方法去整合以上两个阶段的扩散方程以及得到整个暴露周期的氯离子分布表达式。

混凝土中氯离子扩散过程中Cs以线性增加趋于恒定值比Da不断减少趋于恒定值的时间要短，本文以Da趋于恒定值为分界点。暴露时期在多数情况下分为不同条件下的两个阶段。分别为：阶段1，表面氯离子浓度随时间以线性方式增加和氯离子扩散系数随时间减小；阶段2，表面氯离子浓度和扩散系数都趋于恒定值。

(1)阶段1：以线性增加的Cs和不断减小的Da

氯离子扩散过程中的第1阶段，考虑了初始氯离子浓度C0、随时间不断减小扩散系数，在式(9)中用Da替换D，te替换t，得到：

式(10)只适用于恒定的Da而不适用于不断减小的Da。对于在扩散过程中Da值不断减少的情况，Fick第二扩散定律可以改写成式(11)，把Date当成一个整体转变后再代入式(10)：

采纳Crank[3]变换方法，引进一个新的时间参数T′，为：

T′的值可以从式(13)的积分得到。当满足初始边界条件时：te=0,T′=Date=0，确定这个积分的常数为－Drtrmta01－m/(1－m)，其中ta0为阶段1的初始时刻。
令Drtrmf(T)f(H)＝D′，则式(13)为：
把式(14)代入式(10)中得到式(15)，为：
式中，C′是第1阶段混凝土中氯离子浓度。对于第1阶段结束时刻te1，这阶段最终时刻的氯离子分布ΔC′可以用te1替换式(15)中的te得到，说明式(15)适用于Cs随时间以线性方式增加和Da不断减小的扩散过程。

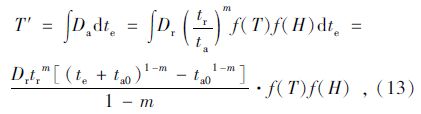
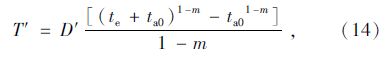
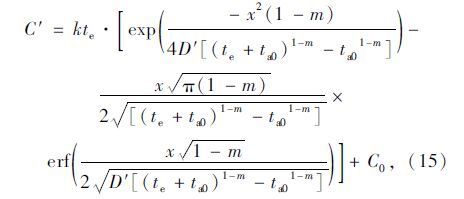
(2)阶段2：恒定的Cs和Da

氯离子扩散过程的第2阶段，Cs和Da都趋于恒定值，式(3)适用此种扩散过程。但是，不能直接使用式(3)，这是因为在阶段2开始时刻通过式(3)计算得到的氯离子分布曲线与式(15)在相同时刻得到的分布曲线不一致。直接利用式(3)来模拟第2阶段的扩散过程，等同于在没有考虑第1阶段分布结果的前提下，就假设扩散过程是在趋于恒定的表面氯离子浓度和扩散系数的条件下进行。用这种方法计算得到的氯离子分布曲线与第1阶段结束时获得的氯离子浓度显著不同。因此，需从阶段2选择一个等效暴露时间，用这个等效暴露时间获得与阶段1结束时相似的分布。等效暴露时间的数学表达式为：

式中，t′e为阶段2的等效暴露时间；Δt′e为实际暴露时间与等效暴露时间的差值。在式(3)中用t′e代替te，并代入其他参数的初始值，得到阶段2氯离子扩散的数学表达为：
式中，C″为第2阶段氯离子浓度；te1为阶段2开始暴露时刻。这里需要选择一个Δte′值，用它通过式(17)计算阶段2开始时刻的分布曲线，且与阶段1结束时刻通过式(15)的分布曲线很接近。整个阶段2氯离子浓度的增量ΔC″为：
式中te2为第2阶段末时刻。

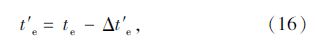
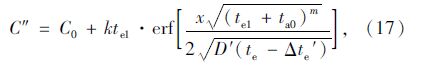
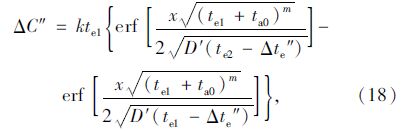
以上整个扩散过程氯离子的最终分布，可以由两个阶段氯离子浓度的增量之和获得：

2 氯离子扩散模型验证 2.1 模型对比分析

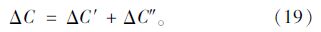
通过计算实例对比分析本文建立的氯离子扩散新方程和已有的扩散方程。假设龄期为28 d的混凝土构件，初始氯离子扩散系数为2.0×10-12m2/s。龄期系数m取0.4，扩散系数随时间的变化按照式(4)计算，温度为20 ℃，相对湿度取90%。通过分析，氯离子扩散系数随暴露时间不断减小趋于恒定值所需时间为7.5 a(即te1为7.5 a)，7.5 a后Cs到达最大值，Cs值取混凝土质量的0.65%。考虑对流区域，Δx取10 mm。混凝土中初始氯离子浓度为混凝土质量的0.01%。混凝土构件养护28 d后将其暴露在含氯离子环境中，开始引起钢筋腐蚀的临界氯离子浓度为混凝土质量的0.06%。

利用上述参数和已知条件，通过式(3)和式(19)，对比分析分别对暴露时间为10，25，50 a的构件的氯离子浓度分布规律。式(3)中的扩散系数D为恒定值，为Dave。

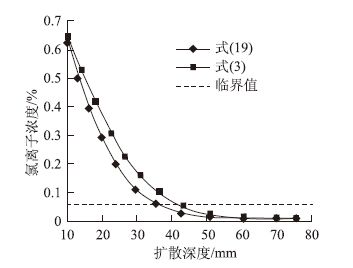
图 1为暴露10 a的混凝土构件的氯离子分布曲线。如图 1所示，当Dave为6.6×10-13 m2/s时，通过式(3)计算的氯离子分布曲线明显比用新模型获得曲线分布要高，可能的原因是式(3)使用的是最大的Cs值，新模型中Cs值是逐渐增加至趋于恒定值，而混凝土中氯离子浓度在一定范围内与Cs是成比例的，表面氯离子缓慢的积累过程将减慢氯离子扩散过程。

图 1 式(19)与(3)氯离子分布曲线 Fig. 1 Chloride ion distribution curves of formula (19) and formula (3)
图选项

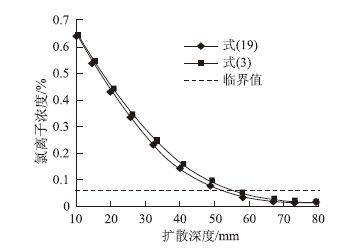
图 2为暴露25 a的混凝土构件的氯离子分布曲线。在式(3)中，Dave为4.3×10-13 m2/s。如图 2所示，用式(19)获得的氯离子分布曲线，比式(3)获得的曲线稍低，最可能的原因是，新方程中同样采用了最大Cs值，式(3)用的Dave值比新方程中的Da值要大。因此，式(3)得到的分布曲线要稍高于式(19)，但二者已经接近。

图 2 式(19)与(3)氯离子分布曲线 Fig. 2 Chloride ion distribution curves of formula (19) and formula (3)
图选项

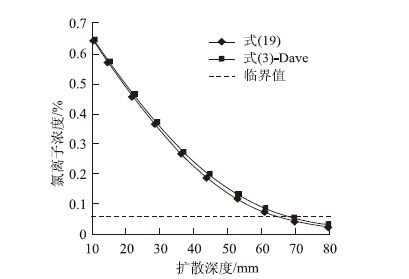
图 3为暴露50 a的混凝土构件的氯离子分布曲线。用新方程获得的曲线与Da取平均值(3.4×10-13 m2/s)通过式(3)获得曲线很接近相似。通过式(3)获得的曲线3这两条曲线之间的总体差异与图 2所得曲线分布差异相比稍微减小。这个阶段，新模型中Cs与Da都是常量，这与式(3)所采用条件基本相同，这也是所得两条曲线更加接近的原因。

图 3 式(19)与(3)氯离子分布曲线 Fig. 3 Chloride ion distribution curves of formula (19) and formula (3)
图选项

从图 1~图 3可以看出，新方程氯离子浓度到达临界值时的扩散深度比基准方程要浅，随着暴露时间的增加，二者之间的差异越来越小，用新方程所得氯离子分布曲线与以往普遍采用的式(3)用平均Da值所得曲线越来越接近，这也充分说明了用新方程所得的氯离子分布与式(3)的氯离子分布曲线的变化趋势是基本一致的。

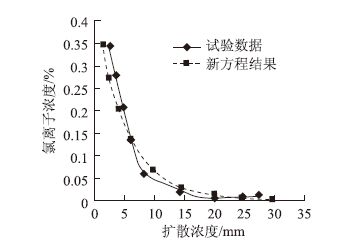
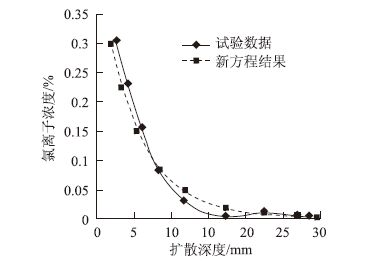
2.2 试验验证

本试验依托长沙理工大学人工气候模拟箱，在考虑不同水灰比的情况下，根据试验配合比制作一批150 mm×150 mm×150 mm的混凝土试块，每组水灰比条件下各制作7个试块，其中6个用于氯离子腐蚀试验，另一个用于强度测试，试块标准养护28 d后，置于试验温度为25 ℃、试验湿度为95%的人工模拟气候箱。在强度测试后取样进行氯离子浓度测试，利用试验数据对比分析验证新方程的正确性。图 4、图 5分别为水灰比0.4,0.5条件下的试验数据与新方程计算氯离子浓度分布曲线。从图中可以看出在扩散深度大于17.5 mm时，氯离子试验测试浓度呈不规律变化，其可能原因是由于暴露于氯盐环境中时间短，在扩散深度大于17.5 mm后，氯离子浓度值不能精确测出，导致试验结果有一定的离散性，但新方程总体变化趋势与试验结果基本一致，新方程能很好地描述混凝土中氯离子扩散过程。

图 4 试验与新方程氯离子分布曲线(w/c=0.4) Fig. 4 Chloride ion distribution curves of test and new equation (w/c=0.4)
图选项

图 5 试验与新方程氯离子分布曲线(w/c=0.5) Fig. 5 Chloride ion distribution curves of test and new equation (w/c=0.5)
图选项
2.3 实桥氯离子浓度分布验证

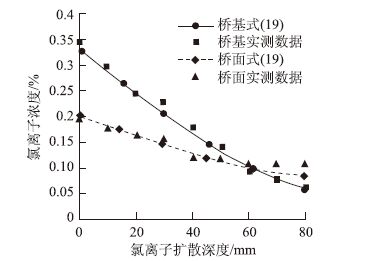
北京西直门旧立交桥，建成于1980年，1999年3月因混凝土破坏维修加固。王玲等[22]研究认为，在除冰盐作用下的盐冻破坏和钢筋锈蚀是混凝土破坏的主要原因。该桥面混凝土的水泥用量为309 kg/m3，配合比为1∶1.82∶2.82，水灰比为0.540。图 6是桥基和桥面混凝土芯样的氯离子浓度的实测结果与本文数学模型的对比分析图。从图 6可以看出，利用理论数学模型所得结果与实测数据基本一致。

图 6 实桥实测数据与模型氯离子分布曲线 Fig. 6 Chloride ion distribution curves based on bridge test data and model
图选项
3 结论

(1)在Fick第二扩散定律的基础上，考虑了表面氯离子浓度有一个缓慢的积累过程，氯离子扩散系数是随时间不断减小的，二者随时间会趋于一个恒定的最大值和最小值，从而把扩散过程分为两个阶段，每个阶段利用适用条件得到扩散方程，然后把两个阶段新方程整合得到新的氯离子扩散方程。新氯离子扩散模型能成功地用于模拟混凝土氯离子扩散过程，把短期试验结果扩展到适用于长期的氯离子扩散过程。

(2)利用以往普遍采用的氯离子扩散方程去验证新的扩散方程，并结合试验数据与新方程作比较验证。混凝土初始时期氯离子扩散系数不断减小，随暴露时间的增加扩散系数继续减小直到趋于恒定值。与Fick第二扩散定律利用平均Da值所得氯离子分布曲线，并结合试验数据作比较验证，发现新氯离子扩散方程，阶段一所需完成时间的增加会导致分布曲线下降。随着暴露时间的增加，新扩散方程与Fick第二扩散定律的扩散方程的变化趋势完全一致，且其效果明显优于Fick第二扩散定律。

(3)采用综合考虑表面氯离子浓度和氯离子扩散系数随暴露时间不断变化直到趋于恒定值条件的氯离子扩散新方程，比用Fick第二扩散定律基准方程得到的到达临界氯离子浓度时的扩散深度要提前约3%～14%，但随着暴露时间的增长，二者之间的差异越来越小。

参考文献
[1] 吴烨,朱雅仙,刘建忠.混凝土氯离子扩散系数时变性规律与计算模型适用性分析[J].水利水运工程学报,2012,(3):50-55. WU Ye,ZHU Ya-xian,LIU Jian-zhong. Time Variation of Concrete Chloride Diffusion Coefficients and Applicability Analysis of the Calculation Models[J]. Hydro-Sciennce and Engineering,2012,(3):50-55.
[2] 万臻,李乔,毛学明.基于可靠度的桥梁结构剩余使用寿命预测方法[J].公路交通科技,2006,23(9):51-53,62. WAN Zhen,LI Qiao,MAO Xue-ming. Methods for Bridge Structure Residual Service Life Prediction Based on Reliability[J]. Journal of Highway and Transportation Research and Development,2006,23(9):51-53,62.
[3] 巴恒静,张武满,高小建.水灰比与应力水平对混凝土氯离子渗透性影响[J].武汉理工大学学报,2006,28(5):45-47,56. BA Heng-jing,ZHANG Wu-man,GAO Xiao-jian. Influence of Water to Cement Ratio and Stress Level on Chloride Penetration Resistance of Concrete[J]. Journal of Wuhan University of Technology, 2006,28(5):45-47,56.
[4] 李国平,胡方健,吴用贤.受力状态下混凝土试件氯离子侵蚀试验(续)[J].预应力技术,2011(6):12-20. LI Guo-ping,HU Fang-jian,WU Yong-xian. Chloride Ion Penetration Test on Concrete Specimens under Stress State[J]. Prestress Technology,2011(6):12-20.
[5] 余红发,孙伟,麻海燕,等.混凝土在多重因素作用下的氯离子扩散方程[J].建筑材料学报,2002,5(3):240-247. YU Hong-fa,SUN Wei,MA Hai-yan,et al. Diffusion Equations of Chloride Ion in Concrete under the Combined Action of Durability Factors[J]. Journal of Building Materials,2002,5(3):240-247.
[6] 路新瀛,杨用兵,刘凯.混凝土中氯离子扩散系数原位测量研究[J].建筑技术,2007,38(1):56-58. LU Xin-ying,YANG Yong-bing,LIU Kai. Preliminary Study of In-situ Measurement of Chloride Diffusivity in Concrete[J]. Architecture Technology,2007,38(1):56-58.
[7] THOMAS M D A,BAMFORTH P B. Modelling Chloride Diffusion in Concrete:Effect of Fly Ash and Slag[J].
[8] PREZZI M,GEYSKENS P, MONTEIRO P J M. Reliability Approach to Service Life Prediction of Concrete Exposed to Marine Environments[J]. ACI Materials Journal,1996,93(6):544-552.
[9] CRANK J. The Mathematics of Diffusion[M]. Oxford:Clarendon Press,1975.
[10] ANDRADE C,DIEZ J M,ALONSO C. Mathematical Modeling of a Concrete Surface "Skin Effect" on Diffusion in Chloride Contaminated Media[J].
[11] ANN K Y,AHN J H,RYOU J R. The Importance of Chloride Content at the Concrete Surface in Assessing the time to Corrosion of Steel in Concrete Structures[J]. Construction and Building Materials,2008,23(1):239-245.
[12] MEIRA G R,ANDRATE C,ALONSO C,et al. Durability of Concrete Structures in Marine Atmosphere Zones:The Use of Chloride Deposition Rate on the Wet Candle as an Environmental Indicator[J].
[13] TANG L, NILSSON L O. Chloride Diffusivity in High Strength Concrete at Different Ages[J].Nordic Concrete Research, 1992, 11(1):162-171.
[14] STANISH K, THOMAS M. The Use of Bulk Diffusion Tests to Establish Time-dependent Concrete Chloride Diffusion Coefficients[J].
[15] 冯乃谦,丁建彤,张新华,等.暴露于海洋环境的高性能混凝土中的氯化物渗透[M]//索默H.高性能混凝土的耐久性.北京:科学出版社, 1998:118-127. PENG Nai-qian, DING Jian-tong, ZHANG Xin-hua, et al. Chloride Penetration of High-performance Concrete Exposed to Marine Environment[M]//SUOMO H. Durability of High Performance Concrete. Beijing:Science Press, 1998:118-127.
[16] PAGE C L, SHORT N R, EL TARRAS A. Diffusion of Chloride Ions in Hardened Cement Pastes[J].
[17] MUSTAFA M A, YUSOF K M. Atmospheric Chloride Penetration into Concrete in Semitropical Marine Environment[J].
[18] COSTA A, APPLETON J. Chloride Penetration into Concrete in Marine Environment-Part 1:Main Parameters Affecting Chloride Penetration[J].
[19] COSTA A, APPLETON J. Chloride Penetration into Concrete in Marine Environment -Part 2:Prediction of Long Term Chloride Penetration[J].
[20] KATO E, KATO Y, UOMOTO T. Development of Simulation Model of Chloride Ion Transportation in Cracked Concrete[J].
[21] SHIN C B, KIM E K. Modeling of Chloride Ion Ingress in Coastal Concrete[J].
[22] 王玲,田培,姚燕,等.西直门旧桥混凝土破坏原因分析[M]//王媛俐,姚燕.水泥基复合材料科学与技术.北京:中国建材工业出版社, 1999:79-82. WANG Lin, TIAN Pei, YAO Yan, et al. Causual Analysis of Concrete Destruction of Xizhimen Old Bridge[M]//WANG Yuan-li, YAO Yan. Science and Technology of Cement-based Composites. Beijing:China Building Materials Press, 1999:79-82.