扩展功能
文章信息
- 何涛, 张巍, 吴植安
- HE Tao, ZHANG Wei, WU Zhi-an
- 基于动静载试验数据的预应力混凝土梁模型修正方法试验研究
- Experimental Research on Model Updating Method of Prestressed Concrete Girder Based on Dynamic and Static Loading Test Data
- 公路交通科技, 2015, Vol. 31 (12): 75-80
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (12): 75-80
- 10.3969/j.issn.1002-0268.2015.12.013
-
文章历史
- 收稿日期: 2015-03-09
预应力混凝土梁的结构性能评估在桥梁工程检测与鉴定领域具有重要的工程意义,但常规检测鉴定方法难以对预应力桥梁构件的整体工作性能做出准确的评估,采用静载试验费用昂贵,且周期较长,不适合普遍使用。因此,通过有限元模型修正方法,建构模型评估预应力混凝土梁的结构性能就成为一种高效的技术手段。
目前的有限元模型修正方法存在着明显的不足。单独采用静载试验数据进行模型修正,有限的荷载步使得可以用于修正的静力测试数据偏少[1];单独应用动载试验数据进行模型修正,动力响应试验存在着试验模态不完备,高阶振型无法准确测量,测试结果受噪声干扰误差较大等缺点[1]。当前采用联合动静载试验数据进行有限元模型修正具有广泛的应用前景。但目前的联合动静载法由于采用不变的加权系数,不能考虑静、动载2个单目标函数在优化迭代过程中在精度和数量级上的差异,容易导致识别效果不佳[2]。本文提出的模型修正方法,综合运用动态加权系数和灵敏度分析方法,联合动静载试验数据,以现场静载试验获得的竖向挠度实测值和动测得到的前5阶自振频率实测数据对基于设计图纸的有限元模型进行修正;而后对修正后的有限元模型按照静载试验加载工况进行加载,模拟分析了静载试验加载工况下2榀预应力混凝土梁有限元模型的应变、挠度计算结果,与现场静载试验测试结果相比较,表明本文提出的方法可以用于对预应力混凝土梁的结构性能评估。
1 现场动静载试验本文动静载试验在中铁三局霍州至永和关高速公路梁场进行,试验对象分别选取1榀跨径40 m的预应力混凝土T梁和1榀跨径30 m的预应力混凝土箱梁。存梁时间均为90 d左右。采用钢垫板和板式橡胶支座作为梁端支座。
1.1 静力测试采用液压千斤顶通过锚桩反力梁装置加载。本试验采用一个等效集中力F施加到试验梁跨中,此等效力F在试验梁加载截面产生的弯矩等于梁在标准使用荷载下该截面的弯矩,具体见表 1。试验分5级加载到等效集中力。
| 试验梁 | 标准使用荷载下跨中截面弯矩/(kN·m) | 等效集中力/ kN |
| 40 m T梁 | 3 693 | 382.30 |
| 30 m箱梁 | 2 643 | 368.50 |
测试方案为:
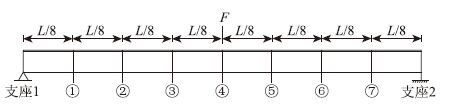
(1)挠度测试:沿梁长方向在2支座中心,L/8,L/4,3L/8,L/2,5L/8,6L/8,7L/8共9个截面处的前后两侧面对称布置测点,采用百分表量测;
(2)应变测试:在跨中位置沿截面前后两侧面上、下缘各布置电阻应变片,采用7V08高级数据记录仪量测。
测点布置和加载位置如图 1所示。
|
| 图 1 测点布置和加载位置 Fig. 1 Arrangement of measuring points and loading positions |
动测仪器主要包括:国家地震局工程力学研究所研发的891-Ⅱ型拾振器、低通滤波放大器、INV-306DF型智能信号采集处理分析仪及DASP6.5.3信号分析处理软件、秦皇岛市信恒电科技有限公司生产的YDL-5H力锤,力锤最大适用范围为300 kN。
2 预应力混凝土梁有限元模型的建立及计算 2.1 初始有限元模型依据设计图纸,采用有限元软件ANSYS建构预应力混凝土梁的实体有限元模型。为使模型符合实际状况,用solid65单元模拟主梁混凝土,用link8单元模拟梁内HRB335钢筋,并通过双线性等向强化本构模型赋予solid65单元3个方向的体积配筋率[3, 4];用link8单元模拟预应力筋,通过节点耦合法与主梁混凝土单元耦合[5]。计入预应力损失,并考虑存梁时间对预应力损失的影响。预应力通过降温法施加[6]:
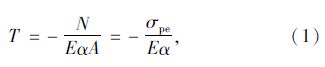
| C50混凝土 | 预应力钢绞线 | HRB335钢筋 | |
| 弹性模量/GPa | 34.5 | 195 | 200 |
| 密度/(kg·m-3) | 2 600 | 7 850 | 7 850 |
| 泊松比 | 0.27 | 0.3 | 0.3 |
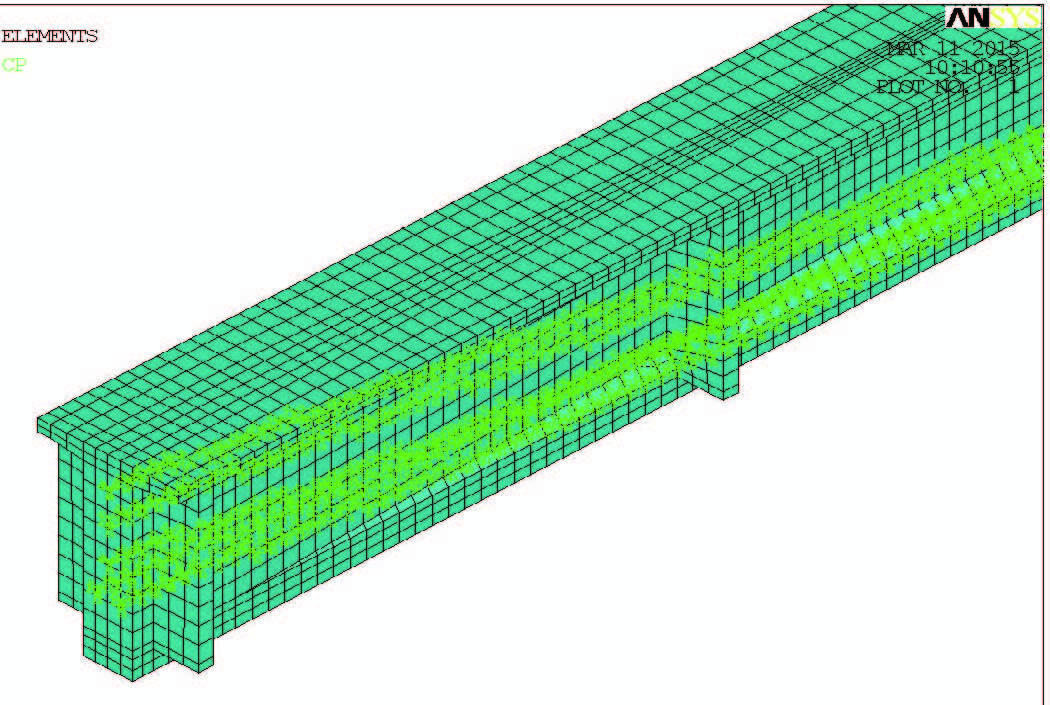
有限元计算模型如图 2、图 3所示。
|
| 图 2 40 m预应力混凝土T梁有限元模型 Fig. 2 FE model of 40 m RC T-girder |

|
| 图 3 30 m预应力混凝土箱梁有限元模型 Fig. 3 FE model of 30 m RC box girder |
目前,国内外学者对预加应力如何影响桥梁结构的动力特性认识还不一致[7, 8, 9]。为考察预应力大小对简支梁自振频率的影响,选取跨径30 m箱梁建模并进行模态分析。预应力筋的布置形式按设计图纸要求,预应力大小按设计值、50%设计值、无预应力3种工况施加,计算构件前5阶竖向自振频率,结果见表 3。
| 预应力工况 | 1阶/Hz | 2阶/Hz | 3阶/Hz | 4阶/Hz | 5阶/Hz |
| 无预应力 | 4.248 | 14.447 | 34.452 | 53.929 | 73.540 |
| 50%设计值 | 4.248 | 14.447 | 34.452 | 53.929 | 73.540 |
| 设计值 | 4.248 | 14.447 | 34.452 | 53.929 | 73.540 |
由表 3的计算结果表明,在预应力混凝土梁未出现开裂的状态下,不同预应力大小对简支梁的自振频率没有影响。这与A.Dall’Asta和Dezi的研究结论相一致[9]。
2.3 初始有限元模型计算结果静力计算和模态分析的数值结果见表 4。
| 项目 | 描述 | T梁试验与计算数据对比 | |||||
| 40 m | 30 m | ||||||
| 实测 | 理论 | 误差/% | 实测 | 理论 | 误差/% | ||
| 竖向 挠度/ mm | 1/8L | 2.524 | 4.136 | 63.87 | 2.902 | 4.664 | 60.72 |
| 1/4L | 8.238 | 8.246 | 0.10 | 5.568 | 8.034 | 44.29 | |
| 3/8L | 10.447 | 10.895 | 4.29 | 7.486 | 11.107 | 48.38 | |
| 跨中 | 11.087 | 11.914 | 7.46 | 9.451 | 12.553 | 32.82 | |
| 5/8L | 9.682 | 10.829 | 11.85 | 8.469 | 11.702 | 38.17 | |
| 3/4L | 7.281 | 7.707 | 5.85 | 6.109 | 9.014 | 47.56 | |
| 7/8L | 1.891 | 2.347 | 24.10 | 3.248 | 5.015 | 58.56 | |
| 竖向 频率/ Hz | 1阶 | 3.850 | 3.881 | 0.81 | 4.500 | 4.252 | 5.51 |
| 2阶 | 13.648 | 12.199 | 10.62 | 16.004 | 14.452 | 9.69 | |
| 3阶 | 19.043 | 18.44 | 3.17 | 38.032 | 34.394 | 9.57 | |
| 4阶 | 27.832 | 28.064 | 0.84 | 56.014 | 53.671 | 4.18 | |
| 5阶 | 45.412 | 43.004 | 5.30 | 78.019 | 73.273 | 6.08 | |
试验结果表明,各测点挠度计算结果相比试验结果偏大,而模态数值分析结果又比试验测试结果偏小,说明在建构有限元初始模型时,结构的刚度取值相比实际值偏小,因此有必要对模型进行修正。
3 目标函数的构造以及参数灵敏度分析 3.1 状态变量根据表 4,L/8,7L/8两个测点挠度实测值与有限元模型计算值的偏差较其他测点大很多,由于L/8,7L/8测点的挠度本来就非常小,导致挠度测试从跨中到梁端测点的误差本身就越来越大,以至L/8,7L/8测点的数据已不能采用。另一方面,百分表的读数误差相较较小的测试值来说也会比较明显,这个误差已远大于本论文想修正的参数误差。因此,本次修正的测试数据采用L/4~3L/4测点的挠度实测值,竖向频率取前5阶实测值,整体误差控制10%。
3.2 目标函数本文采用综合运用动态加权系数和单目标函数作为状态变量的联合动静法构造目标函数[10, 11]:
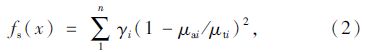
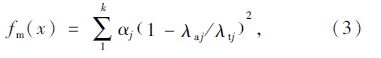



这里需要说明的是,本文综合运用动态加权系数和联合动静法所构造的目标函数,充分考虑了静、动载2个单目标函数在优化迭代过程中在精度和数量级上的差异,克服了以往的目标函数采用不变的加权系数,在迭代计算过程中加权系数不会因各单目标函数数量级的变化而自动调整,导致联合动静法失去“联合”的目的和意义,也避免了当测量精度差、量级大的残差项在修正过程中处于主导地位时所造成识别效果不佳的缺陷[2]。
3.3 设计参数灵敏度分析考虑到钢筋和钢绞线的材料参数,通过单独测试已是比较精确,而混凝土的材料参数受施工因素的影响,与设计值存在偏差,故仅取混凝土弹性模量、密度、泊松比等参数进行灵敏度分析[12, 13]。
目标函数对设计变量的灵敏度为:
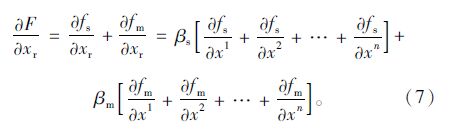
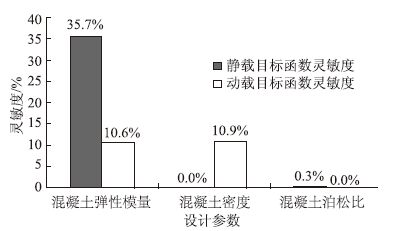
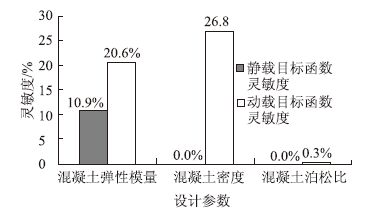
用ansys中的最优梯度法对设计参数进行灵敏度分析,分别得到T梁模型和箱梁模型中设计参数变化±1%,目标函数对于设计参数的绝对灵敏度,见图 4、图 5。
|
| 图 4 40 m T梁目标函数对设计参数灵敏度 Fig. 4 Sensitivity of 40 m T-girder's objective function to design parameters |
|
| 图 5 30 m箱梁目标函数对设计参数灵敏度 Fig. 5 Sensitivity of 30 m box girder's objective function to design parameters |
通过灵敏度分析可见:挠度计算结果对混凝土的弹性模量的变化比较敏感,而频率计算结果对混凝土的弹性模量和密度的变化都比较敏感,混凝土的泊松比则对挠度和频率的计算结果没有影响。故将混凝土的弹性模量、密度选择为进一步的待修正参数。
4 模型修正计算利用有限元软件ANSYS的优化设计模块,用一阶方法[14]进行优化计算,最终得到使目标函数取得最小值的最佳序列计算结果,见表 5。
| 项目 | 描述 | 40 m T梁修正前后数据对比 | 30 m箱梁修正前后数据对比 | ||||||
| 实测值 | 修正值 | 误差/% | 实测值 | 修正值 | 误差/% | ||||
| 修正前 | 修正后 | 修正前 | 修正后 | ||||||
| 竖向挠度/mm | 1/4L | 8.238 | 7.795 | 0.10 | 5.38 | 5.568 | 5.862 | 44.29 | 5.27 |
| 3/8L | 10.447 | 10.288 | 4.29 | 1.52 | 7.486 | 8.094 | 48.38 | 8.13 | |
| 跨中 | 11.087 | 11.242 | 7.46 | 1.40 | 9.451 | 9.152 | 32.82 | 3.17 | |
| 5/8L | 9.682 | 10.132 | 11.85 | 4.65 | 8.469 | 8.524 | 38.17 | 0.65 | |
| 3/4L | 7.281 | 7.286 | 5.85 | 0.07 | 6.109 | 6.575 | 47.56 | 7.63 | |
| 竖向频率/Hz | 1阶 | 3.850 | 4.034 | 0.81 | 4.78 | 4.500 | 4.478 | 5.51 | 0.50 |
| 2阶 | 13.648 | 12.748 | 10.62 | 6.59 | 16.004 | 15.559 | 9.69 | 2.78 | |
| 3阶 | 19.043 | 19.273 | 3.17 | 1.21 | 38.032 | 37.248 | 9.57 | 2.06 | |
| 4阶 | 27.832 | 29.573 | 0.84 | 6.26 | 56.014 | 58.326 | 4.18 | 4.13 | |
| 5阶 | 45.412 | 45.201 | 5.30 | 0.46 | 78.019 | 79.605 | 6.08 | 2.03 | |
多次优化迭代后设计参数修正值,见表 6。
| 设计变量 | 修正前 | 修正后 | 偏差/% | |
| 40 m T梁 | 混凝土弹性模量 | 34.5 | 37.022 | 7.31 |
| 混凝土密度 | 2 600 | 2 541.5 | -3.73 | |
| 30 m箱梁 | 混凝土弹性模量 | 34.5 | 50.234 | 45.61 |
| 混凝土密度 | 2 600 | 3210.1 | 31.02 | |
从表 5、表 6可看出,装配式后张法预应力混凝土梁的弹性模量比设计值增大7.3%~45.6%,这一方面是由于混凝土弹性模量随龄期增长而增长所致[15];另一方面,也考虑到支模偏差、梁内钢筋布置与设计图纸存在偏差,使得梁截面的惯性矩与设计值不符,故本文修正的混凝土弹性模量表征的是对整个构件刚度的修正。
5 静载试验工况下有限元模型数值计算结果与现场静载试验结果的比较为验证本文提出的模型修正方法和精度,将修正后模型按照静载试验加载工况进行加载,模拟分析了静载试验加载工况下梁跨中截面的应变、挠度值,并与现场静载试验测试结果进行了比较。各级加载下跨中下缘混凝土主拉应变和竖向挠度的结果对比见表 7、表 8。
| 荷载步 | 40 mT梁挠度/mm | 30 m箱梁挠度/mm | ||||
| 实测值 | 修正值 | 偏差/% | 实测值 | 修正值 | 偏差/% | |
| 1级 | 1.538 | 1.684 | 9.49 | 1.182 | 1.102 | -6.77 |
| 2级 | 3.609 | 3.717 | 2.99 | 2.986 | 3.159 | 5.79 |
| 3级 | 6.474 | 6.151 | -4.99 | 5.393 | 5.219 | -3.23 |
| 4级 | 8.858 | 8.584 | -3.09 | 7.568 | 7.277 | -3.85 |
| 5级 | 11.087 | 11.242 | 1.40 | 9.451 | 9.152 | -3.17 |
| 荷载步 | 40 m T梁应变/(× 10-6) | 30 m箱梁应变/(×10-6) | ||||
| 实测值 | 修正值 | 偏差/% | 实测值 | 修正值 | 偏差/% | |
| 1级 | 9.17 | 9.34 | 1.81 | 16.42 | 15.10 | -8.07 |
| 2级 | 32.92 | 33.60 | 2.05 | 48.67 | 45.28 | -6.98 |
| 3级 | 56.67 | 58.88 | 3.91 | 81.83 | 75.46 | -7.79 |
| 4级 | 81.17 | 89.17 | 9.86 | 115.00 | 108.64 | -5.53 |
| 5级 | 108.92 | 114.46 | 5.09 | 147.33 | 134.82 | -8.49 |
由表 7~表 8可见,修正后的模型在各级加载下的跨中截面应变值和挠度值都与实测值相当接近,相对误差在10%以内。这说明修正后的模型达到了较高的计算精度,能够反映结构的真实受力与变形。
6 结论(1)本文提出了综合运用动态加权系数和灵敏度分析方法,联合动静载试验数据对预应力混凝土梁进行模型修正。该方法克服了以往模型修正方法的不足,提高了模型修正的精度。
(2)本文提出的模型修正方法通过与现场易于准确测量的静载挠度数据和动测自振频率相结合,能够实现对预应力混凝土梁的结构性能评估。这对探索和完善结构状态评估的工程应用具有参考价值。
| [1] | 宗周红,任伟新.桥梁有限元模型修正和模型确认[M].北京:人民交通出版社,2012. ZONG Zhou-hong, REN Wei-xin. Finite Element Model Updating and Model Validation of Bridge Strustures[M]. Beijing:China Communications Press,2012. |
| [2] | 李波,屈文忠,曾又林.基于有限元模型修正技术的结构损伤检测[J].武汉大学学报:工学版,2008,41(5):102-105. LI Bo, QU Wen-zhong, ZENG You-lin. Research on Structural Damage Detection Based on Finite Element Model Updating[J]. Engineering Journal of Wuhan University, 2008,41(5):102-105. |
| [3] | 王新敏. ANSYS工程结构数值分析[M].北京:人民交通出版社,2007:485-486. WANG Xin-min. ANSYS Numerical Analysis of Engineering Structures[M]. Beijing:China Communications Press,2007. |
| [4] | 王新敏,李义强,许宏伟.ANSYS结构分析单元与应用[M].北京:人民交通出版社,2011. WANG Xin-min, LI Yi-qiang, XU Hong-wei. ANSYS Structure Analysis Units and Its Application[M]. Beijing:China Communications Press, 2011. |
| [5] | 熊健民,周俊荣,周金枝.基于ANSYS预应力简支梁固有频率的研究[J].固体力学学报,2008(增1):158-161. XIONG Jian-min, ZHOU Jun-rong, ZHOU Jin-zhi. Research of Pre-stress Simple-supported Beam's Natural Frequency Based on ANSYS[J]. Chinese Journal of Solid Mechanics, 2008(S1):158-161. |
| [6] | 李辉,阎贵平,高学奎.基于有限元的预应力混凝土梁桥的优化分析[J].基建优化,2005,26(6):107-110. LI Hui,YAN Gui-ping,GAO Xue-kui. Optimization Design of Prestressed Concrete Beam Bridge Base on Finite Element Analysis[J]. Optimization of Capital Construction,2005,26(6):107-110. |
| [7] | 苏健,孙宗光,易南概,等.基于自振频率与神经网络方法的简支梁预应力识别[J].公路交通科技,2013,30(10):39-43. SU Jian,SUN Zong-guang,YI Nan-gai,et al. Prestress Identification for Simple Beam Based on Natural Frequency and Neural Network[J]. Journal of Highway and Transportation Research and Development,2013,30(10):39-43. |
| [8] | 夏樟华,宗周红.预应力对混凝土梁动力特性的影响分析[J].振动与冲击,2007,26(7):129-134. XIA Zhang-hua, ZONG Zhou-hong. Analysis of Influence of Prestressing on Dynamic Characteristics of A Concrete Beam[J]. Journal of Vibration and Shock,2007,26(7):129-134. |
| [9] | DALL'ASTA A, DEZI L. Discussion of "Prestress Force Effect on Vibration Frequency of Concrete Bridges"[J]. |
| [10] | 方志,唐盛华,张国刚,等.基于多状态下静动态测试数据的斜拉桥模型修正[J].中国公路学报,2011,24(1):34-41. FANG Zhi,TANG Sheng-hua,ZHANG Guo-gang,et al. Cable-stayed Bridge Model Updating Based on Static and Dynamic Test Data of Multi-state[J]. China Journal of Highway and Transport, 2011,24(1):34-41. |
| [11] | 何旭辉,李鹏.既有钢管混凝土拱桥的有限元模型修正[J].城市道桥与防洪,2009(1):20-23,7. HE Xu-hui, LI Peng. Finite Element Model Updating of Existing Steel Pipe Concrete Arch Bridge[J]. Urban Roads Bridges & Flood Control, 2009(1):20-23,7. |
| [12] | 狄生奎,李凯峰,项长生,等.简支变连续装配式混凝土箱梁桥的有限元模型修正[J].甘肃科学学报,2013,25(3):107-111. DI Sheng-kui, LI Kai-feng, XIANG Chang-sheng,et al. Finite Element Model Updating of Existing Steel Pipe Concrete Arch Bridge[J].Journal of Gansu Sciences, 2013, 25(3):107-111. |
| [13] | 刘金梅,韩国有,周国强.基于灵敏度分析的井架结构模型修正方法研究[J].科学技术与工程,2009,9(9):2366-2370. LIU Jin-mei,HAN Guo-you,ZHOU Guo-qiang. Research on Model Updating Method of Derrick Structures Based on Sensitivity Analysis[J]. Science Technology and Engineering, 2009,9(9):2366-2370. |
| [14] | 郭彤,李爱群,费庆国,等.零阶与一阶优化算法在悬索桥模型修正中的应用对比分析[J].振动与冲击,2007, 26(4):35-38,68,167-168. GUO Tong,LI Ai-qun, FEI Qing-guo, et al. Application Comparison between Zero-order and First-order Optimization Methods In Model Updating of Suspension Bridges[J]. Journal of Vibration and Shock,2007,26(4):35-38,68,167-168. |
| [15] | 刘宏伟.混凝土早龄期弹性模量无损检测初探[D].南京:河海大学,2006. LIU Hong-wei. Preliminary Discussion of Nondestructive Testing of Elasticity Modulus of Concrete at Early Age Nondestructivly[D].Nanjing:Hohai University,2006. |
 2015, Vol. 31
2015, Vol. 31
