扩展功能
文章信息
- 黄华, 曾志成, 张峰, 刘伯权
- HUANG Hua, ZENG Zhi-cheng, ZHANG Feng, LIU Bo-quan
- 不同桩锚支护结构受力性能及影响因素
- Mechanical Behavior and Influencing Factors of Different Pile-anchor Supporting Structures
- 公路交通科技, 2015, Vol. 31 (12): 58-66
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (12): 58-66
- 10.3969/j.issn.1002-0268.2015.12.011
-
文章历史
- 收稿日期: 2014-09-09
桩锚支护结构是国内外岩土工程支护中应用最为广泛的一类支护结构,主要由抗滑桩、锚杆、围檩和冠梁4部分组成。该支护结构体系根据其锚杆作用的位置不同,本文将其分为两类:桩锚整体式支护结构和桩锚分离式支护结构。前者锚杆直接锚固于抗滑桩桩体之上,省去了围檩结构,但锚杆穿过桩体,预留孔洞减弱了桩身承载力,同时增大了锚杆成孔的施工难度;后者锚杆锚固于围檩上,避免桩体留孔,方便施工。由于锚杆作用位置不同,两类支护结构的受力性能将产生差异。当前研究者对此类支护结构的研究主要集中在桩锚分离式支护结构上:许海勇等[1]根据收集的大量基坑围护结构变形观测结果,研究了桩锚支护结构水平位移的计算方法;李柏生等[2]研究了桩顶荷载、锚杆间距和孔径、锚杆锚固段长度、预应力大小等参数对支护结构内力和变形等的影响;张智浩等[3]对季节性冻土区桩锚支护结构冻胀机理及计算方法进行了研究,并提出了相应处理措施;许锡昌等[4]通过现场实测和数值分析结果,推导了桩锚支护结构的桩顶最大位移解析解,并分析了桩顶荷载、桩间距、锚杆刚度等参数变化对桩顶位移的影响;胡贺松[5]对桩锚支护效应、支护结构与土体相互作用、桩锚结构参数对结构稳定性的影响以及桩锚结构之间的相互作用机理进行研究,建立了桩锚支护结构与土体相互作用模型及其变形协调条件和破坏模式、桩锚数值计算单元等;此外,王明龙等[6]、张钦喜等[7]分别采用FLAC3D软件对桩锚支护结构的力学性能进行了分析。当前对桩锚整体式支护结构研究的缺乏,会导致设计中错误地估算桩锚支护结构的承载力,给支护工程埋下隐患,甚至会引起安全事故。
近年来延安市加快城市化进程,受地域影响不得不大规模开发黄土沟壑和塬、梁、峁区域,形成大量地质结构复杂的高边坡、深基坑,对岩土支护结构的稳定性和受力性能提出了较高要求[8, 9, 10]。因此,论文采用ABAQUS软件,以延安某综合边坡支护为背景,建立三维有限元模型,分析两类支护结构受力性能上的差异,为此类支护结构的设计和使用提供参考。
1 工程概况延安某综合边坡地层构造为第四系全新统素填土(Q4ml),第四系中更新统(Q2eol)黄土、白垩系(K1)泥岩、砂岩等,稳定地下水位埋深约2.60~11.60 m,属于上层滞水,仅分布于场地东侧局部地段,支护结构设计中不考虑地下水对设计影响。该综合边坡为道路、基坑复合边坡,高度5~17 m,基坑回填至设计高度后,道路边坡剩余高度0~12 m;边坡南侧坡顶由近至远为小区道路和场地、建筑,场地上停放车辆,宽15 m;西侧坡顶为市政道路,宽15 m,路面以下有天然气、自来水等管道,道路对面为住宅楼。边坡支护采用桩锚结构,西侧受到用地红线限制,抗滑桩紧邻建筑物,采用桩锚整体式支护结构,南侧采用传统的桩锚分离式支护结构,具体见图 1。施工现场在南侧7,13,16 m支护高度和西侧8 m和11 m支护高度处桩顶分别设置观测点以监测桩顶变形。

|
| 图 1 两类桩锚支护结构 Fig. 1 Two kinds of pile-anchor supporting structure |
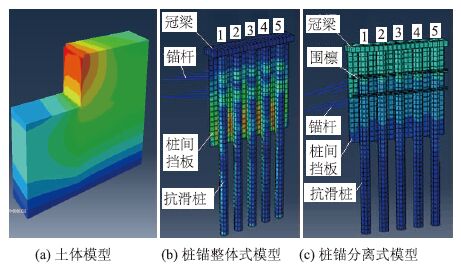
有限元计算模型如图 2,根据工程实际情况进行简化。基本尺寸如下:土体开挖深度取10.0 m,宽度取10.5 m;冠梁尺寸为11.0 m×1.3 m×0.60 m,冠梁顶部标高为±0,坡底标高为-10;锚杆为两根直径28 mm的预应力钢筋,长度20 m,锚杆与水平夹角为15°,上下两排锚杆竖直间距为2.5,2 m、水平间距为2 m;抗滑桩的设计尺寸为长度20 m、直径为1 m、桩心距为2 m、嵌固部分的深度为10 m;桩间土体采用0.15 m厚钢筋混凝土板支档;围檩采用两根20 a槽钢焊接而成。抗滑桩从左至右依次编号为1~5,其中1号桩距左侧1 m,5号桩距右侧0.5 m,两类模型的锚杆高度及位置相同。
|
| 图 2 支护结构有限元模型 Fig. 2 FE model of supporting structures |
抗滑桩、冠梁、桩间挡板均为钢筋混凝土材料,模型中不考虑其配筋,并设置为弹性材料,均采用实体单元C3D8R;围檩为工字钢焊接而成,同样设置为弹性材料并选用C3D8R;锚杆采用等向强化塑性模型和T3D2单元,材料参数见表 1。
| 杆件 | 密度ρ/ (kg·m-3) | 弹性模量 E/MPa | 泊松比ν | 抗拉强度/ MPa | 抗压强度/ MPa |
| 抗滑桩 | 2 400 | 30 000 | 0.2 | 3.0 | 30.0 |
| 冠梁 | 2 400 | 30 000 | 0.2 | 3.0 | 30.0 |
| 挡板 | 2 400 | 28 000 | 0.2 | 2.5 | 25.0 |
| 围檩 | 7 800 | 210 000 | 0.25 | 360 | 360 |
| 锚杆 | 7 800 | 200 000 | 0.25 | — | — |
模型中土体除支护面,坑底以及坡顶外,约束全部自由度。模型中各个部件之间的接触约束分别为:抗滑桩和土体之间采用有限滑移的接触形式,抗滑桩和冠梁、抗滑桩和围檩之间采用绑定约束(Tie)约束,耦合变形,不考虑相对滑移;锚杆和土体之间的约束形式采用嵌入区域(Embedded region),嵌固于土体中,同样不考虑相对滑移。由于模型按实际工程设计建立,结构基本处于弹性状态,并不会出现破坏的极端状态,因此对计算结果造成的影响很小,可以忽略其带来的误差。
3 两类结构基本受力性能比较两类结构模型基本受力性能计算时,除土体、支护结构自重外,根据设计,在坡顶施加20 kPa的荷载,以考虑坡顶道路的车辆、行人以及可能的堆载等。计算得到结构5根桩的最大位移以及弯矩见表 2,桩身水平位移、弯矩和剪力分布见图 3。根据现场监测点分布,西侧11 m高处抗滑桩与计算模型最为接近。根据监测数据,支护结构变形稳定时桩顶水平位移为30.8 mm,与整体式支护结构桩顶最大位移相差8.77%,考虑到计算模型与实际场地的差异,以及顶部实际荷载大小(实际结构顶部荷载小于20 kPa),模型计算结果是可信的,误差在可接受范围。
| 桩号 | 位移/mm | 弯矩/(kN·m-1) | 剪力/kN | ||||||
| 整体式 | 分离式 | 二者差/% | 整体式 | 分离式 | 二者差/% | 整体式 | 分离式 | 二者差/% | |
| 1 | 33.46 | 40.15 | 19.99 | 292.80/-244.40 | 333.79/-283.62 | 14.00/16.05 | 384.77 | 422.01 | 9.68 |
| 2 | 33.73 | 40.48 | 20.01 | 269.91/-213.61 | 277.75/-235.99 | 2.90/10.48 | 353.84 | 394.70 | 11.55 |
| 3 | 33.76 | 40.51 | 19.99 | 258.74/-207.63 | 268.61/-228.23 | 3.81/9.92 | 342.93 | 362.37 | 5.67 |
| 4 | 33.70 | 40.44 | 20.00 | 245.06/-200.38 | 251.15/-213.40 | 2.49/6.50 | 355.68 | 402.27 | 13.10 |
| 5 | 33.38 | 40.06 | 20.01 | 282.79/-236.05 | 311.93/-265.04 | 10.30/12.28 | 379.51 | 409.11 | 7.80 |
| 注:表中弯矩列“/”前为正弯矩及其差值,“/”后为负弯矩及其差值。 | |||||||||
|
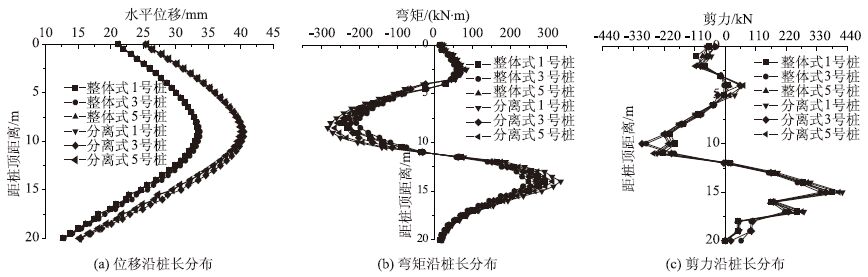
| 图 3 支护结构荷载及位移分布 Fig. 3 Distributions of loads and displacements of supporting structures |
结合表 2和图 3可见,两类支护结构中抗滑桩位移变化趋势相同,水平向位移沿桩长由桩顶至桩底先增大后减小,最大位移出现在距桩顶9.0 m处。并且位于支护结构两端的1号和5号桩变形最小,然后向中间增大,直到中间的3号桩变形达最大,但同类结构抗滑桩之间位移差异不大,整体式支护结构与分离式支护结构位移最大最小值之差仅分别为1.14%和1.12%。但整体式支护结构5根桩最大变形基本上与分离式支护结构相差20%左右,二者差距显著。另外由于结构两端边距不一样,对支护结构存在一定影响,两种结构的5号桩位移均比1号桩略小。
两类支护结构弯矩变化趋势相同,由桩顶至桩底先由正值变为负值,然后再变为正值,弯矩零点出现在距桩顶4.0 m和11.0 m处,负弯矩最大值出现在距桩顶8.0 m处,正弯矩最大值出现在距桩顶14.5 m处,且抗滑桩弯矩由结构两端向中间减小。整体式支护结构抗滑桩正弯矩最大值相差19.48%,负弯矩最大值相差21.97%;分离式支护结构抗滑桩正弯矩最大值相差32.90%,负弯矩最大值相差32.91%。两种支护结构弯矩最大相差16.05%,且支护结构两端的弯矩相差比中间大,两根4号桩正弯矩仅相差2.49%。支护结构两端边距不同,对分离式支护结构弯矩影响要大于整体式,前者5号桩比1号桩小7.01%,后者小3.54%。
两类支护结构剪力变化趋势相同,整体式支护结构剪力最大值出现在10 m和15 m左右处,剪力为零点出现在4 m和12 m处;分离式支护结构剪力最大值出现在10 m和15 m左右处,剪力为零点出现在3,5 m和12 m左右处。两类支护结构的1号桩和5号桩剪力最大,然后向中间的3号桩减小。整体式结构剪力最大值相差12.20%;分离式结构剪力最大值相差16.46%;且整体式支护结构剪力明显小于分离式结构,前者最大值小于后者13.10%。同样,支护结构两端边距对分离式的影响大于整体式,前者5号桩比1号桩小3.15%,后者小1.39%。
以上分析表明两类桩锚支护结构的空间效应明显[11, 12, 13]。两类支护结构荷载和变形产生差异的主要原因是锚杆和抗滑桩连接方式不同,整体式结构锚杆直接锚固在抗滑桩上,其对抗滑桩的约束作用明显大于分离式支护结构;分离式结构锚杆通过围檩与抗滑桩相连接,围檩本身存在变形,导致锚杆对抗滑桩的约束作用减弱。因此,整体式结构连接方式有利于锚杆与抗滑桩的协同作用,但其施工时需预留锚杆孔道,同时增加锚杆成孔时的施工难度。
4 两类结构受力性能的参数分析由于支护结构的抗滑桩直径、桩嵌固长度、冠梁尺寸、锚杆数量、预应力状况等都会影响结构受力性能,下文就针对以上因素,展开参数分析。
4.1 桩径桩径对支护结构受力性能的影响分析主要考虑0.8,1.0,1.2 m这3种桩径,计算模型同图 2,计算得到不同桩径情况下1号桩最大位移以及弯矩见表 3,1号桩桩身水平位移和弯矩分布见图 4。
| 支护桩直径/m | 位移/mm | 弯矩/(kN·m) | ||||
| 整体式 | 分离式 | 二者差/% | 整体式 | 分离式 | 二者差/% | |
| 0.8 | 33.40 | 45.37 | 35.84 | 368.25/-314.18 | 474.99/-412.11 | 28.98/31.17 |
| 1.0 | 33.46 | 40.15 | 19.99 | 292.80/-244.40 | 333.79/-283.62 | 14.00/16.05 |
| 1.2 | 33.09 | 36.40 | 10.00 | 269.27/-232.74 | 325.11/-276.24 | 20.73/18.69 |
| 注: 表中弯矩列“/” 前为正弯矩及其差值,“/”后为负弯矩及其差值。 | ||||||
|
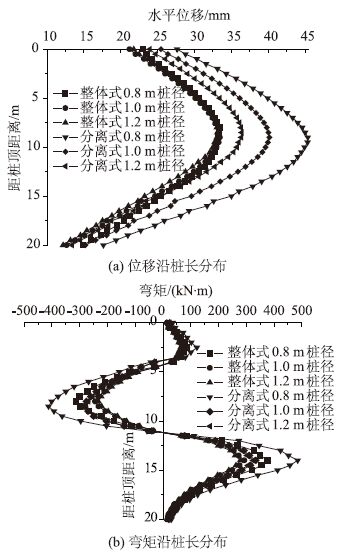
| 图 4 不同桩径时支护结构荷载及位移分布 Fig. 4 Distributions of loads and displacements of supporting structures with different diameters |
根据表 3和图 4可见,不同桩径下两种桩锚支护结构水平位移分布形式相同,但位移差距明显,随桩径增大,二者位移差由35.84%缩小至10%。桩径对整体式支护结构水平位移影响不大,桩体嵌固部分的水平位移有些许变化;而分离式结构随桩径增大,位移减小明显,桩径0.8 m和1.2 m二者相差24.64%。
不同桩径下两种桩锚支护结构弯矩分布形式相同,但弯矩大小差距显著,正负弯矩最大分别相差28.98%和31.17%。两类支护结构在桩径为1.0 m和1.2 m时各自的弯矩曲线差别不大,但是桩径为0.8 m时,弯矩均显著变大,且桩锚分离式情况下桩径0.8 m时的弯矩曲线增大幅度比桩锚整体式更加明显,与1.2 m桩径相比,最大相差49.19%,而后者最大相差37.76%。
随着抗滑桩桩径的增大两种桩锚支护结构的水平位移和弯矩值都呈现出减小的趋势,增大桩径可以减少支护结构的水平位移和弯矩值,尤其是分离式支护结构的效果更为显著;但桩径增大对整体式支护结构的位移影响不明显。并且当桩径增大至一定值时,继续增加抗滑桩的桩径对于支护结构水平位移值和弯矩值的影响不再明显。
4.2 嵌固深度嵌固深度对支护结构的受力性能影响分析主要考虑8,10 m和12 m,这3种情况。计算模型同图 2,计算得到不同嵌固深度情况下1号桩最大位移以及弯矩见表 4,1号桩桩身水平位移和弯矩分布见图 5。
| 嵌固深度/m | 位移/mm | 弯矩/(kN·m) | ||||
| 整体式 | 分离式 | 二者差/% | 整体式 | 分离式 | 二者差/% | |
| 8 | 34.79 | 41.29 | 18.68 | 368.20/-297.72 | 472.34/-393.89 | 28.28/32. 30 |
| 10 | 33.46 | 40.15 | 19.99 | 292.80/-244.40 | 333.79/-283.62 | 14.00/16.05 |
| 12 | 31.69 | 35.50 | 12.02 | 348.40/-312.95 | 459.70/-397.25 | 31.95/26.94 |
| 注:表中弯矩列“/” 前为正弯矩及其差值 ,“/” 后为负弯矩及其差值。 | ||||||
|
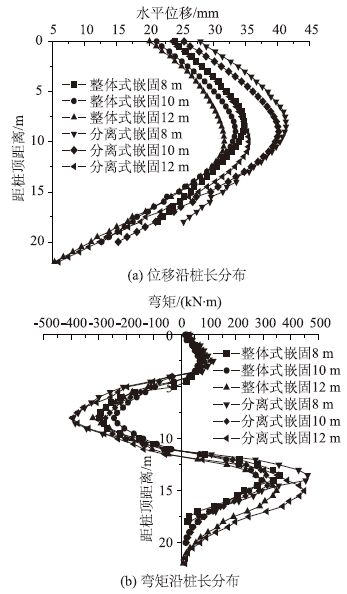
| 图 5 不同嵌固深度时支护结构荷载及位移分布 Fig. 5 Distributions of loads and displacements of supporting structures with different nesting depths |
根据表 4和图 5可见,不同嵌固深度下两种桩锚支护结构水平位移分布形式相同,桩身水平位移最大值点随着嵌固深度的增加而下移,且桩顶水平位移减小。但整体式支护结构位移增大幅度要小于分离式结构,前者8 m和12 m深度的最大值相差9.78%,而后者相差16.31%。嵌固8 m和 12 m时,两类支护结构最大位移差接近,分别为18.68%和19.99%,但随嵌固深度进一步增大,两类支护结构最大位移差缩小为12.02%。
不同嵌固深度下两种桩锚支护结构弯矩分布形式相同,嵌固深度增大时抗滑桩负弯矩最大值作用点变化不明显,但正弯矩最大值点逐渐下移。两种桩锚支护结构在嵌固10 m时的弯矩值要明显小于嵌固8 m和嵌固12 m时的弯矩值,整体式结构最大正弯矩分别相差25.75%和18.99%;而分离式情况下嵌固10 m的弯矩值要小得更明显,最大正弯矩分别相差41.51%和37.72%。同时,嵌固10 m时两类结构的弯矩最大值相差也最小,正负弯矩最大值相差仅为14%和16.05%。这说明增大或者减小嵌固深度,不一定使得结构受力更为合理。
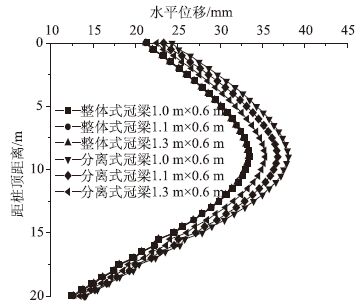
4.3 冠梁尺寸冠梁尺寸对支护结构的受力性能影响分析主要考虑1.0 m×0.6 m,1.1 m×0.6 m和1.3 m×0.6 m,3种情况。计算模型同图 2,计算得到不同冠梁情况下1号桩最大位移见表 5,1号桩桩身水平位移分布见图 6。由于3种冠梁尺寸下,弯矩几乎没有变化,考虑篇幅,这里不再给出。
| 冠梁截面尺寸/(m×m) | 位移/mm | ||
| 整体式 | 分离式 | 二者差/% | |
| 1.0×0.6 | 33.51 | 41.91 | 25.07 |
| 1.1×0.6 | 33.46 | 40.15 | 19.99 |
| 1.3×0.6 | 33.33 | 37.46 | 12.39 |
|
| 图 6 不同冠梁尺寸时支护结构位移分布 Fig. 6 Distributions of displacements of supporting structures with different sizes of top-beam |
根据表 5和图 6可见,冠梁尺寸增大,体系刚度增加,对抗滑桩的约束作用增大,因此结构体系位移减小,但其对桩锚整体式结构的影响不大。而桩锚分离式结构随冠梁尺寸减小,位移分别增大7.18%和11.88%。同时,两类结构的最大位移随冠梁尺寸减小,差距增大,由12.39%增大至25.07%。
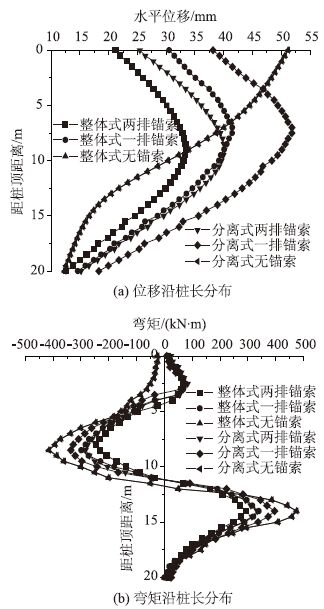
4.4 锚索数量锚杆数量对支护结构的受力性能影响分析主要考虑两排、一排和无锚杆3种情况。计算模型同图 2,计算得到不同锚杆数量情况下1号桩最大位移及弯矩见表 6,1号桩桩身水平位移及弯矩分布见图 7。
| 锚杆数量 | 位移/mm | 弯矩/(kN·m) | ||||
| 整体式 | 分离式 | 二者差/% | 整体式 | 分离式 | 二者差/% | |
| 两排锚杆 | 33.46 | 40.15 | 19.99 | 292.80/-244.40 | 333.79/-283.62 | 14.00/16.05 |
| 一排锚杆 | 41.49 | 51.86 | 25.00 | 349.60/-298.90 | 386.63/-336.66 | 10.59/12.63 |
| 无锚杆 | 55.68 | 55.68 | — | 475.13/-415.27 | 475.13/-415.27 | —/— |
| 注:表中弯矩列“/”前为正弯矩及其差值,“/”后为负弯矩及其差值。 | ||||||
|
| 图 7 不同锚杆数量时支护结构荷载及位移分布 Fig. 7 Distributions of loads and displacements of supporting structures with different amounts of anchor blot |
根据表 6和图 7可见,两类支护结构在不设置锚杆时,抗滑桩水平位移分布曲线重合,桩身下部水平位移变小,上部位移变大,且桩身位移最大值出现在桩顶。支护结构施加锚杆后,抗滑桩底部水平位移沿桩长向桩顶逐渐增大,到桩身中部时达到最大值,然后至桩顶水平位移逐渐减小。设置两排锚杆时,桩身水平位移最大值位置下移,水平位移值显著减小,整体式支护结构最大位移减小22.90%,而分离式减小29.17%,且两类结构最大位移差值由25%减小到18.93%。但两类支护结构水平位移分布曲线的整体趋势未有明显的变化。
两类支护结构在不设置锚杆时,抗滑桩弯矩分布曲线重合,桩顶部不存在正弯矩区,而设置锚杆时,桩顶0~4 m范围是正弯矩分布区,锚杆对支护结构产生的锚固力改变了桩身弯矩曲线的分布,随锚杆数量增加,弯矩最大值减小,整体式结构最大正弯矩分别减小35.91%和62.27%,分离式结构最大正弯矩分别减小22.89%和42.34%,且随锚杆数增多,两类结构的最大弯矩差值增大。这说明锚杆对整体式结构的约束效果好于分离式结构。
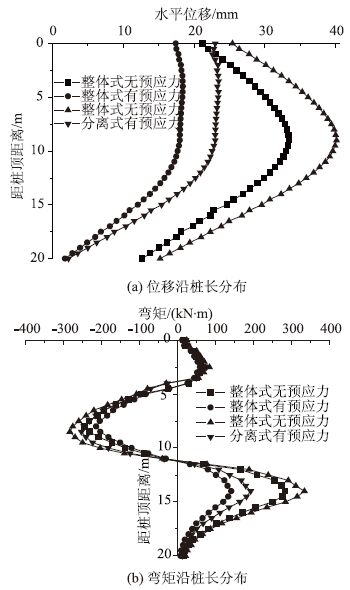
4.5 锚杆预应力锚杆预应力对支护结构的受力性能影响分析主要考虑不施加预应力和施加120 kN预应力两种情况,预应力通过降温法施加。计算模型同图 2,计算得到不同锚杆数量情况下1号桩最大位移及弯矩见表 7,1号桩桩身水平位移及弯矩分布见图 8。
| 预应力 | 位移/mm | 弯矩/(kN·m) | ||||
| 整体式 | 分离式 | 二者差/% | 整体式 | 分离式 | 二者差/% | |
| 施加 | 18.43 | 23.48 | 27.40 | 141.44/-214.30 | 192.27/-253.23 | 35.94/18.17 |
| 未施加 | 33.46 | 40.15 | 19.99 | 292.80/-244.40 | 333.79/-283.62 | 14.00/16.05 |
|
| 图 8 不同预应力时支护结构荷载及位移分布 Fig. 8 Distributions of loads and displacements of supporting structures with different pre-stresses |
根据表 7和图 8可见,两类支护结构在锚杆未施加和施加预应力时,抗滑桩桩身水平位移分布曲线发生明显变化,施加预应力时抗滑桩上部悬臂段水平位移基本相同,最大位移下降显著,整体式结构最大位移下降81.55%,分离式下降71%。
锚杆施加预应力后,抗滑桩弯矩分布形式没有改变,但弯矩大小显著降低。锚杆施加200 kN预应力后,整体式支护结构负弯矩最大值减少了14.05%,正弯矩最大值减小了2.07倍;分离式支护结构的负弯矩最大值减少了12%,正弯矩值减少了1.74倍。由此可见对锚杆施加预应力后可以显著减小桩身的位移和弯矩。
5 桩锚支护结构计算调整国内外现行边坡支护规程中没有把桩锚支护结构分成两类来分别计算,基于上文的数值分析结果可知,两种桩锚支护结构中抗滑桩的位移和内力存在显著变化,现根据以上计算,分析调整计算的必要性。
根据表 2中的计算结果,2,3,4号桩弯矩相差最大10.49%,最小2.48%,而1~5号桩的剪力差5.67%~13.1%,因此两类支护结构受力上的差异并不十分明显。但支护结构中间部分抗滑桩与端部抗滑桩受力差异显著:整体式支护结构抗滑桩正弯矩最大值相差19.48%,负弯矩最大值相差21.97%,剪力最大值相差12.20%;分离式支护结构抗滑桩正弯矩最大值相差32.90%,负弯矩最大值相差32.91%,剪力最大值相差16.46%。
因此,两类支护结构承载力设计的调整在于支护结构端部构件,可从计算上将其抗弯承载力乘以1.35的调整系数,抗剪承载力乘以1.2的调整系数,将端部的两根桩承载力提高,尤其在一字型边坡支护时,两端没有其他方向的支护结构或土体支撑,此时考虑提高端部结构承载力尤其重要。
6 结论(1) 两类支护结构各自抗滑桩的变形基本一致,支护结构整体性和变形协调性良好。
(2) 两类桩锚支护结构的位移和荷载存在明显的空间效应。变形由两端向中间减小,而弯矩和剪力则由两端向中间增大,中间部分支护结构的受力和变形基本一致,设计时要加强两端抗滑桩的承载力。支护结构端部两根抗滑桩的弯矩和剪力宜分别乘以1.35和1.2的承载力调整系数,以提高其承载力。
(3) 桩锚整体式支护结构中抗滑桩的受力和变形明显小于桩锚分离式支护结构。正常情况下(不包括抗滑桩嵌固深度很深,冠梁尺寸很大等特殊情况),桩锚整体式结构可以有效减少20%以上的最大位移,减少3%以上的最大弯矩值和6%以上的最大剪力值。
(4) 增大抗滑桩桩径,两种桩锚支护结构的水平位移和弯矩值都呈现减小的趋势,同时两类结构的受力和变形差异减小,桩径增大对分离式支护结构的力学性能影响更为显著,而对整体式支护结构的变形影响不明显。
(5) 增大抗滑桩嵌固深度,可减小两类支护结构的位移,但弯矩先减小后增大,且改变幅度较大,整体式结构弯矩差最大达到25.75%,分离式结构弯矩差最大达到41.51%,且分离式结构的受力和变形比整体式结构改变更为显著,增大或者减小嵌固深度,结构受力不一定合理。
(6) 增大冠梁尺寸可提高支护结构整体刚度和抗变形能力,且对分离式结构的影响更大,但其作用有限,对结构的受力影响更小。
(7) 增加锚杆数量、施加预应力可显著减少抗滑桩的水平位移和弯矩,并改变位移和弯矩沿桩身的分布形态,且明显增大两类桩锚支护结构在位移和弯矩上的差值。
| [1] | 许海勇,陈龙珠,刘全林.桩锚支护结构水平位移的简化算法[J].岩土力学,2013,34(8):2323-2328. XU Hai-yong,CHEN Long-zhu,LIU Quan-lin. A Simplified Algorithm of Lateral Displacements of Pile-anchor Retaining Structures[J]. Rock and Soil Mechanics,2013,34(8):2323-2328. |
| [2] | 李柏生,张浩龙,朱彦鹏,等.深基坑桩锚支护结构设计参数分析[J].兰州理工大学学报,2013,39(1):109-114. LI Bo-sheng,ZHANG Hao-long,ZHU Yan-peng,et al. Design Parameters Analysis of Pile-anchor Supporting Structure for Deep Foundation Pit[J]. Journal of Lanzhou University of Technology,2013,39(1):109-114. |
| [3] | 张智浩,马凛,韩晓猛,等.季节性冻土区深基坑桩锚支护结构冻胀变形控制研究[J].岩土工程学报,2012,34(增1):65-71. ZHANG Zhi-hao,MA Lin,HAN Xiao-meng,et al. Frost Heaving Deformation Control of Pile-anchor Retaining Structure of Deep Foundation Pits in Seasonal Frozen Soil Regions[J]. Chinese Journal of Geotechnical Engineering,2012,34(S1):65-71. |
| [4] | 许锡昌,葛修润.基于最小势能原理的桩锚支护结构空间变形分析[J].岩土力学,2006,27(5):705-710. XU Xi-chang,GE Xiu-run. Application of Principle of Minimum Potential Energy to Spatial Deformation Analysis for Deep Foundation Pit with Anchored Pile Supporting[J]. Rock and Soil Mechanics,2006,27(5):705-710. |
| [5] | 胡贺松.深基坑桩锚支护结构稳定性及受力变形特性研究[D].长沙:中南大学,2009. HU He-song. Study on Mechanical Deformation Characteristics and Stability of Deep Foundation with Pile-anchor Structure[D]. Changsha:Central South University,2009. |
| [6] | 王明龙,王景梅.深基坑桩锚支护中桩内力变化规律数值模拟研究[J].地下空间与工程学报,2013,9(3):576-584,627. WANG Ming-long,WANG Jing-mei. Numerical Simulation on the Variation Law of Pile Internal Force of Pile-anchor Retaining Structure in Deep Foundation Pit[J]. Chinese Journal of Underground Space and Engineering,2013,9(3):576-584,627. |
| [7] | 张钦喜,樊绍峰,周予启.深基坑桩锚支护侧土压力反分析及数值模拟[J].岩石力学与工程学报,2009,28(增1):3214-3220. ZHANG Qin-xi,FAN Shao-feng,ZHOU Yu-qi. Back Analysis and Numerical Simulation of Earth Pressure around Pile-anchor Supporting Structures in Deep Pit[J]. Chinese Journal of Rock Mechanics and Engineering,2009,28(S1):3214-3220. |
| [8] | 刘鸣,黄华,韩冰,等.延安地区某边坡双排抗滑桩支护分析[J].长安大学学报:自然科学版,2011,31(2):63-67. LIU Ming,HUANG Hua,HAN Bing,et al. Analysis on Double-row Anti-slide Piles of Slope in Yanan[J]. Journal of Chang'an University:Natural Science Edition,2011,31(2):63-67. |
| [9] | 石玉玲,李貅,李凯玲.锚索抗滑桩工程的优化设计研究[J].工程地质学报,2007,15(3):412-415,327. SHI Yu-ling,LI Xiu,LI Kai-ling. Design Optimizing of Anti-sliding Pile with Prestressed Cable Anchors[J]. Journal of Engineering Geology,2007,15(3):412-415,327. |
| [10] | 杨明辉,汪罗成,赵明华.考虑土拱效应的双排抗滑桩桩侧土压力计算[J].公路交通科技,2011,28(10):12-17,39. YANG Ming-hui,WANG Luo-cheng,ZHAO Ming-hua. Calculation of Soil Pressure against Double-row Anti-slide Piles Considering Soil Arching Effect[J]. Journal of Highway and Transportation Research and Development,2011,28(10):12-17,39. |
| [11] | 张伟园.深基坑桩锚支护体系的空间效应研究[D].邯郸:河北工程大学,2013. ZHANG Wei-yuan. Study on Spatial Effect of Pile-anchor Supported System in Deep Foundation Pit[D]. Handan:Hebei University of Engineering,2013. |
| [12] | 李宝平,张玉,李军.桩锚式支护结构的变形特性研究[J].地下空间与工程学报,2007,3(7):1291-1294. LI Bao-ping,ZHANG Yu,LI Jun. Research on the Deformation Character of Anchor Piles Retaining Structure[J]. Chinese Journal of Underground Space and Engineering,2007,3(7):1291-1294. |
| [13] | 李会章,冯君,宋响军.滑坡推力在多排抗滑桩上的分配情况研究[J].公路交通科技,2014,31(10):26-31. LI Hui-zhang,FENG Jun,SONG Xiang-jun. Research of Thrust-sharing in Multi-row Anti-slide Piles[J]. Journal of Highway and Transportation Research and Development,2014,31(10):26-31. |
 2015, Vol. 31
2015, Vol. 31
