扩展功能
文章信息
- 张海峰, 魏连雨, 宋杨, 马士宾, 虞秋富
- ZHANG Hai-feng, WEI Lian-yu, SONG Yang, MA Shi-bin, YU Qiu-fu
- 基于安定理论的高速公路路面大修结构极限荷载研究
- Research on Structural Ultimate Load of Highway Pavement Overhaul Based on Shakedown Theory
- 公路交通科技, 2015, Vol. 31 (12): 53-57
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (12): 53-57
- 10.3969/j.issn.1002-0268.2015.12.010
-
文章历史
- 收稿日期: 2015-10-23
2. 华北高速公路股份有限公司, 北京 100176;
3. 河北工程技术高等专科学校, 河北沧州 061000
2. Huabei Expressway Co., Ltd., Beijing 100176, China;
3. Hebei Engineering and Technical College, Cangzhou Hebei 061000, China
公路是国民经济快速发展、促进社会进步和保障人民生活的重要公共基础设施,同时也是衡量一个国家现代化进程和经济实力的重要指标[1]。目前我国公路总里程已经达到446.39万公里,其中国家高速公路已突破11万公里。由此带来的养护工作也急剧上升,尤其是早期修建的高速公路相继进入大修周期[2],而我国目前对高速公路的大修养护设计并未形成系统的设计方法。如何科学合理进行高速公路大修结构设计成为养护决策部门面临的一个主要问题。胡霞光等[3]利用均匀设计方法进行路面结构优化,这种方法精确程度高,计算机程序仿真取得了较好的效果,但计算机程序的编写给工程设计人员带来不便。长江大学的黄文雄[4]将遗传算法应用于路面结构的优化设计,作为一种广泛应用的优化算法,遗传算法具有较好的优化性能,然而其缺点是容易陷入局部最优且收敛速度慢的缺点。许新权[5]、俞竞伟应用模糊理论对路面结构进行评价,提供了路面结构的优选模型。该方法需要较高的数学基础,难以在现实生产中推广应用。
上述设计方法在进行路面大修结构设计时各有利弊,然而却均未考虑移动荷载冲击作用的影响,本文则是考虑到高速公路最低速度的限制,分析了行车速率对路面大修结构安定极限荷载的影响。
1 路面大修结构安定理论静力安定定理又称Melan定理[6],表述如下:如果存在一组自平衡残余应力场ρij且不随时间变化,对于任意荷载在给定的极限状态范围不会发生任何变化,将它与假设结构处于完全弹性状态下的应力场σije相加后,结构处满足不屈服条件[7],即:
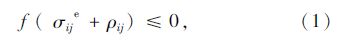
如果对于任何的初始残余应力分布ρij 能够使结构达到安定,则结构在经历足够多的循环次数后的安定残余应力分布当然不会随时间变化。如果用ρ0ij表示结构安定时的残余应力场,由上述定义则有:
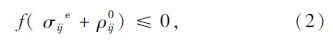
路面结构在实际工作中,承受车辆重复荷载作用[8],为了模拟路面结构实际工作状态,在对路面结构安定分析时,采用循环荷载的加载方式。因此,详细地研究结构承受循环加载的弹性一理想塑性结构的响应具有重要的意义。引入广义荷载Γa(t)。对一个周期为T的循环加载过程,必定有:
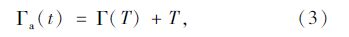
基于Melan静力安定理论下安定荷载乘子求解具体步骤为:
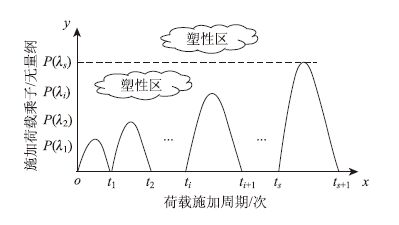
(1)图 1中,物体从O点加载到点P(λ1),然后卸载到点t1,此过程为一荷载步。卸载后观察结构是否进入塑性区域,若进入了塑性区域,则重复加载该过程O→P(λ1) →t1,直到结构内部形成稳定的残余应力场停止循环,然后继续施加荷载步P(λ2);若路面结构没有点进入塑性区,则直接加载到下一加载点P(λ3)。
|
| 图 1 残余应力场求解的加载方式 Fig. 1 Loading ways for solving residual stress field |
(2)重复步骤(1),假设结构加载到已经出现塑性区的加载点P(λi)时,结构内部形成了稳定的残余应力场,表明结构屈服,则停止施加荷载,上一个加载点即为该结构极限安定状态下的临界点,则安定荷载乘子λs=λi-1;若结构内部不能形成稳定的残余应力场,继续施加下一个加载点P(λi+1)。
(3)继续加载,直到结构内部形成稳定的残余应力场得到其对应的荷载乘子即为结构的安定乘子λs。 循环荷载作用下,结构从全部为弹性状态到进入塑性状态,再到形成稳定的残余应力场需要若干的荷载加载过程,对于路面结构来讲即需要在通车运营后的若干周期。对安定荷载乘子可以通过试算来确定,结构的安定性分析和弹塑性分析是同时完成的,不需进行静力安定定理中的纯弹性应力场的计算,且避免了基于数学规划方法的维数障碍,简化了分析步聚。
路面结构材料达到破坏后,塑性变形会不断发展,与破坏前是截然不同的。建立材料的应力-应变关系就必须弄清楚在什么情况下路面材料达到破坏,因此就要给出一个判别破坏与否的标准,即屈服准则。屈服准则可定义为:
(1)物体处于单向受力状态时,只要物体内某一质点的单向应力达到物体的屈服点,则认为该物体开始由弹性状态进入塑性状态,即物体进入屈服阶段。
(2)物体处于多向受力状态时,必须考虑每种应力分量同时作用。在特定的条件(变形速度、变形温度等)下,只有当各个应力分量满足某种关系时,物体才开始进入塑性变形状态,这种条件状态称为屈服准则,又称塑性条件[9]。它是描述受力物体处于不同应力状态下进入塑性状态并使塑性变形继续发展必须遵守的力学准则,这种力学准则一般可表示为:

Kf为试验的常数。若f (σij)= Kf,则结构破坏;若f(σij)Kf ,则结构材料不会产生破坏;f (σij)> Kf的情况不存在。由于破坏与坐标的选取无关,故函数f(σij)的自变量是某种形式的应力不变量,一般取主应力分量。
函数f(σij)在主应力空间内代表的是一曲面,即破坏面。若表示应力状态的点落在破坏面以内,则材料不会破坏;若落在破坏面上,材料破坏。应力状态不可能超出破坏面,破坏面应该可以说是应力空间内达到破坏的所有点的轨迹集合,对路面结构材料的破坏准则,本文采用Drucker-Prager屈服准则。
为了克服Mises准则没有考虑到水压力对屈服与破坏的影响,Drucker与Prager于1952年一起提出了考虑静水压力作用下的广义Mises屈服与破坏准则[10, 11],简称为D-P屈服或破坏准则,D-P准则是广义上的Mises准则的一种形式。D-P准则或称广义Mises准则的屈服函数可表示为:
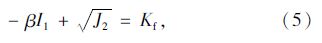
在ANSYS分析中,采用的D-P准则的当量应力计算公式如式(5),但当当量应力σe达到结构材料的屈服应力Kf时,材料将发生塑性应变;若σe小于Kf时,材料将处于弹性状态,其应力的发展趋势将满足弹性应力-应变关系,当量应力可以表示为:
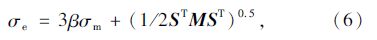
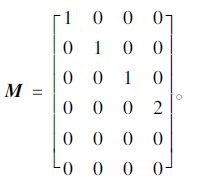
在ANSYS的Help手册里,将式(6)可进一步表示为:
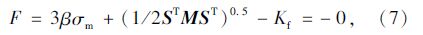
经过调查分析,本文选取高速公路常用的典型大修结构(4 cm AC-13,6 cm AC-20,12~16 cm泡沫乳化沥青再生,16~18 cm水泥稳定碎石,16~20 cm现场冷再生)作为计算模型,参考《公路沥青路面结构设计规范》 (JTG D50—2006)选取结构参数如表 1所示。在对大修路面结构的安定性进行有限元计算分析时,需首先对路面结构模型进行合适的简化处理,本文在进行模拟分析时作如下假设:
(1)路面材料是均匀分布的、各向同性的弹性体,D-P模型应用于冷再生结构层,建模时冷再生材料的内摩擦角取40°、黏聚力C取35 MPa,其他参数见表 1;
| 材料类型 | 层位 | 抗压模量/MPa | 泊松比 | |
| 15 ℃ | 20 ℃ | |||
| 沥青冷再生 | 下面层 | 1000,1200,1400 | 800,1000,1200 | 0.25 |
| 水泥稳定碎石 | 基层 | 3000,3500,4200 | 1300~1700 | 0.25 |
| 水泥冷再生 | 基层 | 1400,1800,2200 | 1000~1400 | 0.25 |
| 铣刨后路面 | — | — | 100~250 | 0.35 |
(2)将土基看作水平向和竖直向下的半无限体,其他大修结构层水平向(路线走向方向)无限,厚度有限。经过验证,荷载作用范围可以近似看作以荷载为中心向外发散的半球,半径超过2.5 m时边缘的影响可以忽略,本文有限元模型以荷载为中心左右延伸3 m,向下延伸5 m,即6 m×6 m×5m;
(3)结构模型侧面边界条件为水平垂直面向约束,底面边界条件全约束;
(4)不计材料自重。
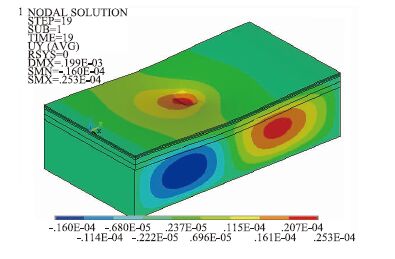
3 沥青路面大修结构安定极限荷载路面大修结构使用寿命大小与其可以承受的极限荷载水平直接相关[12, 13],本文选取典型大修结构为代表结构,根据以上材料参数运用有限元分析软件ANSYS建立路面大修结构仿真模型如图 3所示,计算不同工况下路面大修结构安定极限荷载,计算结果如图 2~图 6所示。
|
| 图 2 移动荷载作用下路面大修结构安定分析模型 Fig. 2 Pavement overhaul structure stability analysis model under moving load |
|
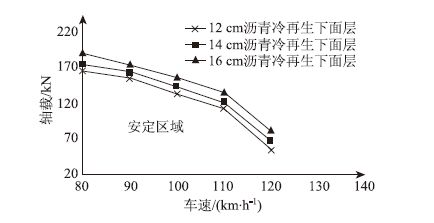
| 图 3 沥青冷再生下面层厚度对结构安定极限荷载的影响 Fig. 3 Influence of thickness on ultimate load of structure shakedown during asphalt cold regeneration |
|
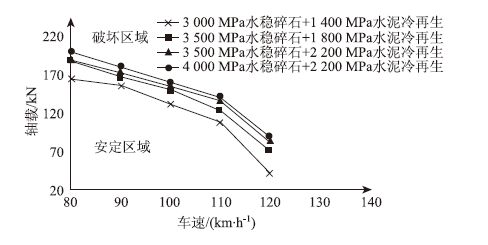
| 图 6 半刚性基层模量对结构安定极限荷载的影响 Fig. 6 Influence of semi-rigid base thickness modulus on ultimate load of structure shakedown |
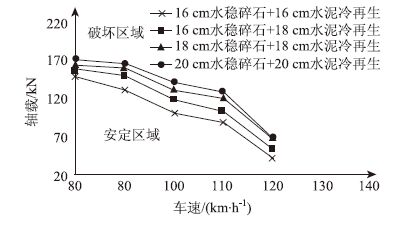
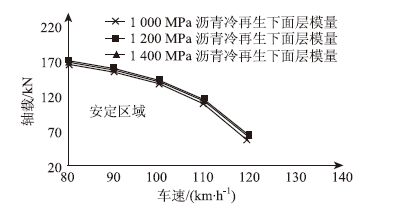
由图 3~图 6可以看出,车速与轴载呈现负相关关系,根据以往经验,高速公路大货车低速行驶会促进车辙的发展,但是显然,高速行驶状态下的车辆对路面的冲击作用对路面结构造成的损伤更大。而且随着路面结构层厚度和回弹模量的增加,路面大修结构安定区域的面积均随之扩大,说明增大路面结构厚度以及模量可以提高路面结构强度。由图 3可以看出,随着沥青冷再生下面层厚度的从6 cm增加到10 cm(增幅66.67%),路面可以承受的安定极限荷载逐渐变大,平均增幅为21.97%,最大增幅达到了45.45%。由图 4看出,随着半刚性基层总厚度由32 cm增加到40 cm(增幅25%),大修结构安定极限荷载增幅均值达到了37.67%,最大增幅为61.90%,最小为14.67%。图 5中,随着沥青冷再生下面层回弹模量从1000 MPa增加到1400 MPa(增幅40%),路面大修结构安定极限荷载增幅均值只有5.76%,最大为12.73%,最小2.98%。图 6中,随着半刚性基层材料回弹模量从3000MPa水稳碎石、1400MPa水泥冷再生增加到4000MPa水稳碎石、2200MPa水泥冷再生,路面大修结构安定极限荷载增幅均值为40.18%,最大值114.63%,最小值15.38%。从每种参数对路面大修结构安定极限荷载提高的贡献度角度看,由小到大依次为:沥青冷再生下面层回弹模量0.14,沥青冷再生下面层厚度0.33,半刚性基层材料回弹模量0.98,半刚性基层总厚度1.51。
|
| 图 4 半刚性基层厚度对结构安定极限荷载的影响 Fig. 4 Influence of semi-rigid base thickness on ultimate load of structure shakedown |
|
| 图 5 沥青冷再生下面层模量对结构安定极限荷载的影响 Fig. 5 Influence of surface course modulus on ultimate load of structure shakedown during asphalt cold regeneration |
4 结论
高速公路由于其功能定位原因,其行驶的车辆行驶速度最低为80 km/h,因此路面承受车辆冲击荷载不能忽视。本文基于shakedown定理,通过建立路面大修结构材料的屈服准则,应用ANSYS模拟高速公路路面大修结构在循环荷载反复作用下的达到塑性破坏时的安定极限荷载,得出如下结论:
(1)行车速度与路面结构安定极限荷载呈负相关关系,行车速度越大,路面大修结构在重复荷载作用下达到塑性破坏时承受的安定极限荷载越小。
(2)路面大修结构层厚度和模量参数取值对其安定极限荷载有一定程度的影响,通过提高路面大修结构层厚度和回弹模量可以提高路面大修结构强度,不同参数对其安定极限荷载提高的贡献度不同,贡献度从小到大依次为:沥青冷再生下面层回弹模量0.14,沥青冷再生下面层厚度0.33,半刚性基层材料回弹模量0.98,半刚性基层总厚度1.51。
(3)在高速公路沥青路面大修结构设计的影响因素诸多,基于安定理论的极限荷载分析可以充实完善大修设计体系,具有较强的借鉴意义。
| [1] | 张桂娟.安徽省高速公路土地利用现状与管理模式研究[D].合肥:安徽农业大学,2012. ZHANG Gui-juan. Research on Present Situation of Land Utilization and Management Mode of Expressway in Anhui Province[D].Hefei:Anhui Agricultural University,2012. |
| [2] | 高菲.重载交通干线公路沥青路面大修关键技术研究[D].天津:河北工业大学,2012. GAO Fei. Research on Overhaul Key Technology of Asphalt Pavement for Arterial Highway with Heavy Load[D]. Tianjin:Hebei University of Technology,2012. |
| [3] | 胡霞光,杨永红,王选仓,等.沥青路面结构优化的均匀设计方法[J].长安大学学报:自然科学版,2002,22(6):15-18. HU Xia-guang,YANG Yong-hong,WANG Xuan-cang,et al. Uniform Design in Structure Optimization of Asphalt Pavement[J]. Journal of Chang'an University:Natural Science Edition, 2002,22(6):15-18. |
| [4] | 黄文雄,谭利英,许成祥.长寿命沥青路面结构力学特性研究[J].公路交通技术,2009,12(5):27-30. HUANG Wen-xiong,TAN Li-ying,XU Cheng-xiang. Study on Mechanical Characteristics of Long Lifetime Asphalt Pavement Structure[J].Technology of Highway and Transport, 2009,12(5):27-30. |
| [5] | 许新权,郑南翔,吴传海,等.基于模糊理论的沥青路面结构优选[J].中外公路,2009,29(4):66-69. XU Xin-quan,ZHENG Nan-xiang,WU Chuan-hai,et al. Optimization of Asphalt Pavement Structure Based on Fuzzy Theory[J]. Journal of China & Foreign Highway, 2009,29(4):66-69. |
| [6] | ARNOLD G, DAWSON A, HUGHES D, et al. The Application of Shakedown Approach to Granular Pavement Layers[C]//9th International Conference on Asphalt Pavements. Copenhagen:International Society for Asphalt Pavements, 2002. |
| [7] | 王生楠,陈瑞峰,诸德培.结构弹塑性安定性分析方法[J].西北工业大学学报,1995,13(4):505-510. WANG Sheng-nan,CHEN Rui-feng,ZHU De-pei. Elasto-plastic Shakedown Analysis Method for Complicated Structures[J]. Journal of Northwestern Polytechnical University, 1995,13(4):505-510. |
| [8] | KERZREHO J P, HORNYCH P, CHABOT A, et al. Evaluation of the Aggressiveness of Different Multi-axle Loads Using Accelerated Pavement Tests[C]//4th International Conference on Accelerated Pavement Testing. Davis CA:Transportation Research Board, 2012. |
| [9] | CHEN H F, PONTER A R S. The Linear Matching Method for Shakedown and Limit Analyses Applied to Rolling and Sliding Point Contact Problems[J].Road Materials and Pavement Design,2005,11(6):9-30. |
| [10] | 孙阳.结构安定性数值分析方法及其工程应用研究[D].上海:上海交通大学,2011. SUN Yang. Numerical Analysis Method of Structure Shakedown and Its Engineering Application[D]. Shanghai:Shanghai Jiaotong University, 2011. |
| [11] | LEVY N H, ITAI E, TIM H. Cyclic Shakedown of Piles Subjected to Two-dimensional Lateral Loading[J]. |
| [12] | 任瑞波,祁文洋,李美玲.移动荷载作用下饱和沥青路面动力响应三维有限元分析[J].公路交通科技,2011,28(9):11-16. REN Rui-bo,QI Wen-yang,LI Mei-ling. Analysis on Dynamic Response of Saturated Asphalt Pavement under Moving Vehicle Loads by 3D Finite Element Method[J]. Journal of Highway and Transportation Research and Development,2011,28(9):11-16. |
| [13] | 张艳红,申爱琴,郭寅川,等.不同类型基层沥青路面设计指标的控制[J].长安大学学报,2011,31(1):6-11. ZHANG Yan-hong, SHENG Ai-qin, GUO Yin-chuan,et al. Control of Designing Indices for Asphalt Pavement with Different Types of Base[J]. Journal of Chang'an University,2011,31(1):6-11. |
 2015, Vol. 31
2015, Vol. 31
