扩展功能
文章信息
- 卢守峰, 王杰, 薛智规, 刘喜敏
- LU Shou-feng, WANG Jie, XUE Zhi-gui, LIU Xi-min
- 基于二流体模型的交通分析及OD出行时间矩阵
- Analysis of Traffic Based on Two-fluid Model and OD travel time matrix
- 公路交通科技, 2015, Vol. 31 (11): 132-137,142
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (11): 132-137,142
- 10.3969/j.issn.1002-0268.2015.11.021
-
文章历史
- 收稿日期: 2014-06-18
2. 长沙市公安局交通警察支队, 湖南 长沙 410012
2. Changsha Traffic Police Detachment, Changsha Municipal Public Security Bureau, Changsha Hunan 410012, China
OD矩阵是进行交通规划与管理的核心基础数据和前提条件,无论是交通规划阶段的4阶段法还是交通管理阶段的智能交通技术,都需要充分详实的OD矩阵,研究获得实时OD矩阵的理论技术具有重要的价值。胡优[1]为减少OD调查数据量,对抽样矩阵优化模型进行了研究。传统的OD出行矩阵调查利用家庭访问法、路边询问法、车辆牌照法和明信片调查法等获取,不仅调查耗时长、成本大、需要大量的人力物力,而且有些调查方法回收率低、需要大量的后续数据处理工作,效率较低,有的调查方法对交通运行造成一定干扰,易引发延误甚至堵塞,需要交警部门的协调配合[2]。80年代末以来,有较多的研究人员做了利用OD反推技术获得OD矩阵的努力,如周晶等[3]用极大似然法原理建立了非线性规划模型,根据先验OD矩阵推算当前OD出行分布矩阵。段进宇等[4]给出了适于计算机编程的模型和算法,提出使用Bi-Section和Newton-Raphson组合算法来保证其中非线性方程求解的稳定性和效率。王炜等[5]提出了一种修正的极大熵模型来推算OD矩阵,并将立足点从路段转移到路径,适用于大型网络OD矩阵推算。董敬欣等[6]提出了用浮动车监测实时OD矩阵的方法,并给出了浮动车与运营车辆的比例随OD对变化的估算模型,但OD反推技术受模型算法及路网流量的影响很大,反推得到的OD矩阵具有很大的不确定性。
事实上,在4阶段模型中,OD矩阵的每个元素代表小区域之间出行量,然后通过方式划分和交通分配两个阶段获得各路段的流量和饱和度。由OD矩阵分配得到的路径时间(阻抗)与现实之间存在一定的误差,局部区域无法反映交通状况甚至与实际情况完全不同。动态交通分配模型自20世纪70年代以来一直在研究,但是要建立一个能够考虑出行需求的动态性、车辆在路段上运动的动态性、适合大规模路网应用的动态交通分配模型还较困难。
对于出行者而言,对交通状态感知最直观的变量是出行时间。在科技迅速发展的今天,许多城市的出租车普遍安装了GPS装置,能够实时向控制中心上传海量的数据,可以从其中直接推算出OD出行时间矩阵,本身就包含了出行需求的动态性和路段上运行的动态性。本文尝试利用出租车的GPS数据获得出行时间,利用二流体模型对数据进行处理,推算城市路网的OD出行时间矩阵。
1 二流体模型简介二流体模型(Two-fluid model)是由Herman和Prigogine[7]在上世纪70年代末提出的,认为车辆的单位距离行程时间T和单位距离停驶时间Ts能够描述路网的宏观特性,并假设它们之间存在某种曲线关系。随后Ardekani和Herman[8]通过地面和高空数据用遍历的方法验证了二流体模型的假设关系,Williams等[9]用测试车和仿真的方法标定了二流体模型的参数,并进一步验证了假设。S. Y. Hong等[10]用GPS数据研究了判定停驶车辆临界速度的阈值。Dixit[11]分析了受事故率、道路线形、信号灯密度等影响因素的驾驶行为对二流体模型参数的影响。国内学者姚荣涵等[12]根据二流体理论,利用流量守恒方程建立了拥挤交通流当量排队长度模型。王殿海等[13]提出了将最佳路网容量与二流体模型结合起来判断路网宏观交通状态。二流体模型将整个路网中的车辆划分为运动车辆和停驶车辆,其中停驶车辆指由于信号灯、道路拥堵等引起停车排队的车辆,而不包括路边或停车场泊车或临时停车(上下客)的情况。二流体模型的两个基本假设如下:
(1)车辆平均行驶速度vr与运动车辆占总车辆数的比值fr成比例关系。
(2)在足够长的时间内探测车辆的停驶时间占行程时间的比例Ts/T与路网内所有车辆的总停驶时间占总行程时间的比例相等。
以上两个基本假设用数学语言表述如下:


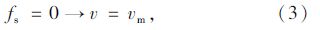

假设平均行程速度v与平均行驶速度vr成正比,且满足式(5):

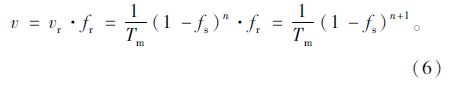
又由于v=1/T,代入式(6)中:
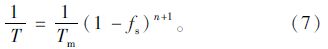
由式(7)最终得到:
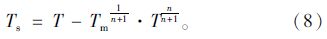
从式(8)可知,城市道路网络的交通特性(Ts,Tr)关系可以用数据点对(Tm,n)来表示,不同的宏观交通特性和对交通变化的敏感性都对应于不同的(Tm,n)点对,因此二流体模型不仅可以刻画一个城市整体的宏观特性,也可以用来描述不同小区域路网的宏观交通特性。
2 数据的采集与处理本文的数据来源是2013-04-23(星期二)全天长沙市6 000 veh出租车的GPS数据,截取7:30:00—8:30:00之间的数据,GPS终端平均每30 s向控制中心上传一次该车的经纬度、速度等数据。
2.1 研究范围的确定(1)经纬度范围。交通区域的划分既要符合数据量的要求又要保证计算效率,因此并不是一味的追求大区域,也不是为了计算简便而缩小研究范围而导致数据不具代表性、不能用二流体模型反映路网宏观特性。综合长沙市城市布局和路网结构以及数据处理过程的效率,最终确定了研究范围为湘江路、八一路、车站路、新建路围合的矩形区域,经度范围为112.957°~113.009 515°,纬度范围为28.1577°~28.204 509°。
(2)时间范围。交通量具有时间分布特性,不同时间段(如高峰期、平峰期)的交通特性存在显著差异,如果研究的时间范围过广,一是会无端增加数据处理的难度、降低计算效率,二是在计算过程中个别变量会被平均化而导致局部特性扁平化,宏观规律无法被发现。综合长沙市交通量时间分布特性和计算效率,最终确定的时间范围为7:30:00—8:30:00。
(3)小区域划分。二流体模型得到的是一定时间、空间范围内的平均值,对城市道路管理者与使用者来说要同时关注大区域和小区域交通状况的好坏,因此还需把研究范围划分为小区域。为了统计和计算方便,同时考虑二流体特性的完整性,将研究范围划分为5行5列方格网状,每个小区边长为1 027 m× 1 034 m。
2.2 统计量及统计方法的确定二流体指的是运动车辆和停驶车辆两个流体,分别用行驶时间Tr和停驶时间Ts来表征,且它们都是每km的时间平均值,因此还需统计车辆行驶距离。
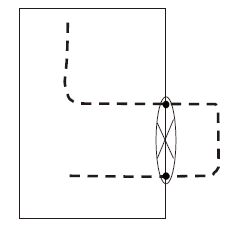
对于二流体指标值Tr和Ts,由于GPS终端上传时间间隔并不是严格以30 s为准,因此用数据点数来推算时间是不准确的,而且在取基准点作为计算起点时有向前计算与向后计算两种情况,加之划分研究范围时车辆行驶轨迹可能不完全落在研究范围内,车辆的连续行驶轨迹会被切断,因此需要确定一种计算方法。本文采用向后计算方法,即以某辆车在处理时间范围内的第1个数据点作为计算起点,与其相邻时间为30 s左右的下一个数据点组成一个数据对,依次向后进行计算。当车辆轨迹超出区域边缘时,将超出部分做切除处理,最终保留所有车辆在研究范围内的轨迹点。图 1所示的是将1辆车超出研究范围的轨迹切除后,变成两段轨迹。标注成黑圆点的两个数据点在时间上不相邻,因此不能作为一个数据对。
|
| 图 1 车辆轨迹分析方法 Fig. 1 Vehicle trajectory analysis method |
由于数据存在一定的原始误差或噪点,因此在数据处理过程中需要进行一些必要的筛选与校正,归纳关键点如下:
(1)将上传时间间隔较长的数据点对隔断。在数据处理过程中发现有3种情况需要将数据点对隔断,一是因交通拥堵状况而停车;二是车辆熄火停车;三是车辆经过交叉口时校正转向距离,由于相邻两个数据点之间的距离是通过经纬度坐标计算的几何距离,而不是行驶轨迹经过的距离,因此在交叉口处的行驶距离误差较大。对这3种情况,本文将时间间隔大于2 min的点对隔断,“后点”作为下一个数据对的起点。
(2)由于GPS终端的机械误差,导致相邻两数据点之间(时间间隔为30 s)的距离偏移很大,表现为瞬时速度过高甚至超过合理范围,还会产生连续数据点速度不为零但彼此的距离为零,表现为“卡死”现象。这两种误差都会对数据处理产生较大影响,因此都应剔除。
(3)删除重复记录的点。由于设备自身故障导致同一个数据点可能会上传不止一次,虽然对距离统计没有影响,但是会导致二流体时间的重复累加,使计算结果失真。
(4)停车速度阈值,即判断车辆处于停驶状态时的速度值。城市路网二流体中的停驶车辆不能简单、绝对地用速度为零来判断,这是由于:①城市路网中移动缓慢的车辆很多,当达到一定程度时,这些车辆也可认为是由于交通状况拥堵而导致的停驶车辆;②GPS数据上传时存在误差,速度的精度不够高;③当发生交通堵塞时,排队后方车辆并不立刻停车,而是慢慢减速到与前方车辆保持到一定的安全距离。Ardekani等[8]研究发现取停车速度阈值4 km/h 会达到较好效果,本文引用该成果,视停车速度阈值小于5 km/h的车辆为停驶车辆。
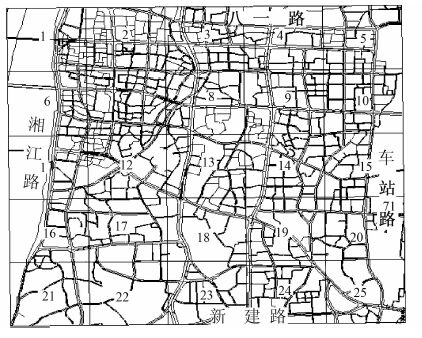
3 OD出行时间矩阵计算方法将研究区域划分为25个小区域,如图 2所示,这里的小区域比OD调查小区要大得多。首先对每个小区域的出租车GPS数据用二流体模型进行分析并进行数据拟合。在得到研究区域内每个小区域的二流体特性后(出行时间特性),以每个小区域为节点运用图论方法进行出行时间最短路径识别,从而达到行车诱导的目的。行车诱导的思路是在车辆起讫小区域确定的情况下,根据每个小区域的二流体曲线特性,对车辆经过的小区域进行诱导,避免经过拥堵的小区域。相对于搜索最优路径的个体诱导方法,这种诱导思路更适于可变信息屏的群体性诱导。
|
| 图 2 路网及小区域划分 Fig. 2 Road network and zone dividing |
3.1 小区域二流体特性
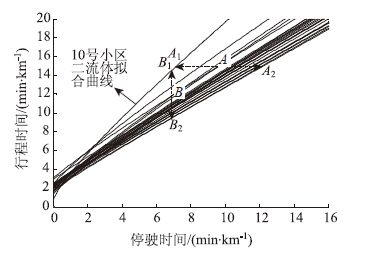
对25个小区域进行二流体计算,每个小区域的特性点对(Tm,n)如表 1所示。将每个小区域的特性参数值表示成式(8)的函数关系并画在同一个坐标系中,如图 3所示。
| (3.098,0.53) | (2.947,0.278) | (2.22,1.46) | (1.61,0.79) | (2.31,0.4) |
| (2.23,0.36) | (1.63,0.75) | (2.24,0.28) | (2.33,0.17) | (0.86,3.4) |
| (1.41,0.99) | (2.23,0.64) | (2.18,0.51) | (2.38,0.24) | (2.1,0.25) |
| (1.74,1.09) | (1.74,1.18) | (2.28,0.58) | (2.15,0.6) | (2.48,0.34) |
| (1.82,0.27) | (2.48,1.12) | (2.11,0.62) | (2.42,0.36) | (2.02,0.19) |
|
| 图 3 25个小区域二流体拟合曲线 Fig. 3 Two-fluid model fitted curves of 25 zones |
从表 1和图 3可以看出,不同小区域的二流体特性曲线可以通过Tm和n进行刻画,Tm的取值范围为0.86~3.098 min/km,此时对应的自由流速度在19.4~69.8 km/h之间,n的取值范围为0.17~3.4。
有了Tm和n,行程时间T与停驶时间Ts之间的关系可通过式(8)计算。二流体特性曲线近似为直线,其截距为Tm,反映在该小区域内通行单位距离需要的最小行程时间,其值越小说明该小区域道路等级越高、路网建设越好。斜率反映行程时间随停驶时间变化的速度,斜率越大,行程时间随停驶时间增长得越快,说明该小区域饱和度较大,交通较拥挤。对于研究区域,各小区域的二流体特性曲线越集中,说明该区域不同小区域的路网建设和承担的交通量越接近。图 3中10号小区域的Tm最小,斜率最大,说明该小区域路网建设最好。A线表示不同小区域在同一行程时间下停驶时间的差异,其长度越小说明各小区域之间的差别越小。对比分析A1点和A2点可知,这两个小区域的单位距离行程时间相同,但是A2点的停驶时间比A1点的停驶时间大,则A2点对应的小区域的行驶时间较小,说明该小区域可能存在多个堵点,在堵点之外的路段运行速度很快。A1点对应的小区域堵点较少,但是总体运行速度较慢。B线表示不同小区域在同一停驶时间下行程时间的差异,B线长度越小说明各小区域之间的差异越小。对比分析B1点和B2点可知,这两个小区域的单位距离停驶时间相同,但是B2点的行程时间比B1点的行程时间小,说明B2点对应的小区域总体运行速度较大。
3.2 OD最短出行时间计算利用矩阵迭代法[2]进行最短路径的识别具有能一次获得任意两点之间最短路权矩阵的优势,在城市交通中,每个小区域都可能成为起讫点的情况下更有应用价值,其算法步骤如下。
步骤1:构造出行时间矩阵。
步骤2:矩阵给出了节点间只经过1步(1条边)到达某点的最短出行时间。
步骤3:对出行时间矩阵进行如下迭代运算,便可得到经过两步达到某点的最短出行时间。
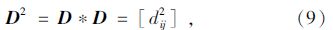
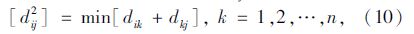
经过m步到达某节点的最短出行时间为:
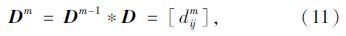
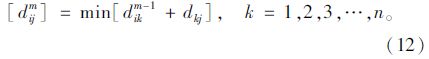
迭代不断进行,直到Dm=Dm-1,即Dm中的每个元素等于Dm-1中的每个元素为止,此时的Dm便是任意两点之间的最短出行时间矩阵。
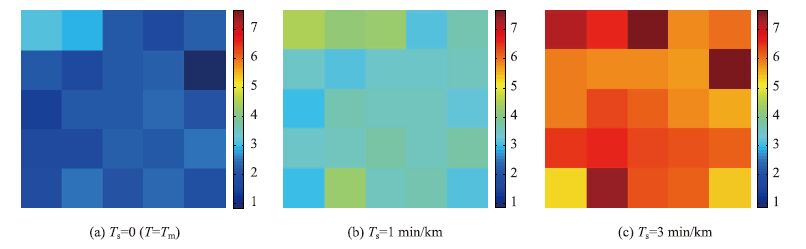
本文的矩阵迭代法中取相邻两小区域之间的行程时间T为阻抗。因为不同停驶时间Ts对应不同的行程时间,因此首先取Ts为一个固定值,在固定Ts值的情况下寻找最短路径,再对比不同Ts取值时最短路径的变化。由于Ts的变化反映了交通状况的变化,因此利用图 4所示的二流体曲线可以得到不同拥堵情况下的行程时间最短路径,这就是拥挤效应在路径诱导中的体现。
|
| 图 4 不同Ts下的各小区域T值变化过程(单位:min/km) Fig. 4 T values of different zones varying with Ts(unit:min/km) |
3种Ts取值下行程时间T的变化过程如图 4所示。每个方格代表 1个小区域,小区域标号与图 2标号相同(略)。可以看出,不同小区域对交通变化的敏感度是不同的,标号为3,10,22的小区域对拥堵较敏感。越敏感的小区域在交通诱导时应尽量避免选择该小区域,因为这些小区域较脆弱。当Ts=1 min/km 时,矩阵经过9次迭代达到迭代标准,即D9=D8,此时的OD出行时间矩阵如表 2所示。文中的方法是根据每个小区域平均行程时间的加和得到不同小区域间的行程时间,可用于诱导长距离的跨区域出行。
| 小区域 | 1 | 2 | 3 | 4 | 5 | … | 21 | 22 | 23 | 24 | 25 |
| 1 | 4.535 | 8.714 992 | 17.170 31 | 24.617 48 | 31.417 09 | … | 27.770 54 | 35.126 97 | 42.922 64 | 49.848 38 | 56.193 73 |
| 2 | 8.714 992 | 4.179 8 | 8.455 323 | 15.902 48 | 22.702 1 | … | 33.748 44 | 29.421 14 | 36.141 37 | 42.461 79 | 48.807 15 |
| 3 | 17.170 31 | 8.455 323 | 4.275 6 | 7.447 161 | 14.246 78 | … | 40.772 55 | 36.445 25 | 42.933 23 | 35.639 12 | 41.984 48 |
| 4 | 24.617 48 | 15.902 48 | 7.447 161 | 3.171 6 | 6.799 618 | … | 46.605 95 | 42.278 65 | 35.486 07 | 28.191 96 | 34.537 32 |
| 5 | 31.417 09 | 22.702 1 | 14.246 78 | 6.799 618 | 3.628 0 | … | 53.405 56 | 49.078 27 | 42.15594 | 34.861 82 | 28.106 65 |
| … | … | … | … | … | … | … | … | … | … | … | … |
| 21 | 27.770 54 | 33.748 44 | 40.772 55 | 46.605 95 | 53.405 56 | … | 3.028 0 | 7.356 425 | 15.269 21 | 22.563 32 | 29.443 83 |
| 22 | 35.126 97 | 29.421 14 | 36.445 25 | 42.278 65 | 49.078 27 | … | 7.356 425 | 4.328 4 | 7.9127 84 | 15.206 9 | 22.087 4 |
| 23 | 42.922 64 | 35.643 73 | 29.406 17 | 35.239 57 | 42.039 19 | … | 15.269 21 | 7.912 784 | 3.584 4 | 7.2941 15 | 14.174 62 |
| 24 | 49.848 38 | 42.461 79 | 35.639 12 | 28.191 96 | 34.987 16 | … | 22.563 32 | 15.206 9 | 7.294 115 | 3.709 7 | 6.880 506 |
| 25 | 56.193 73 | 48.807 15 | 41.984 48 | 34.537 32 | 28.106 65 | … | 29.318 49 | 21.962 07 | 14.049 28 | 6.755 17 | 3.170 8 |
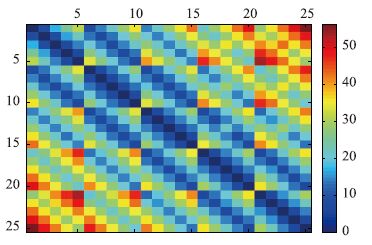
将表 2的内容用matlab的imagesc作灰度图,如图 5所示。可以看出,如果不同小区域的交通状况是相同的,那么随着出行距离的增长,出行时间将增长,对应的颜色应越深。因为小区域是5行5列的,所以灰度图色块每隔5个颜色由浅变深,但某小区域向四周相邻小区域前进时颜色变化程度不一致,这既可以说是路径决策的原因也可以说是路径决策的结果,为解释交通状况和进行路径诱导提供了依据。
|
| 图 5 OD出行时间矩阵灰度图 Fig. 5 Gray scale image of OD travel time matrix |
设某最短路径的起点为r,终点为s,路径辨识算法步骤如下。
步骤1:从起点r开始,寻找与r相邻的节点i,使其满足
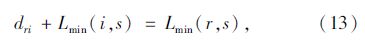
则路段[r,i]便是从r到s最短径路上的一段。
步骤2:寻找与i相邻的一点j,使其满足
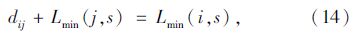
步骤3:如此不断反复,直到终点s。把节点r,i,j,…,s连接起来,便得到从r到s的最短路线。
以小区域1到小区域25的最短路径为例,经过最短路径的反向追踪,确定了最短行程时间路径为1-6-7-8-9-10-15-20-25(数字为图 2中的小区域编号),其他任意两个小区域间的最短路径以此类推。二流体模型给出了一个区域行程时间与停驶时间的平均关系,因此本方法不能给出每个小区域内的最优路线,只能给出将小区域看作节点的最优出行路径,适合于对路网较熟悉的驾驶员采用可变信息屏进行长距离出行的诱导。
4 结论(1)提出了利用出租车GPS数据推导二流体曲线的数据处理方法,并对如何利用二流体曲线分析区域路网的交通状况进行了研究。将研究区域划分成小区域,用所有小区域二流体曲线的离散程度来判断各小区域交通状态的差别,对于交通供需平衡管理有较大参考意义。
(2)建立了利用二流体模型推算出行时间OD矩阵的方法,通过分析不同停驶时间下行程时间T的变化,可以分析各小区域的敏感性和脆弱性,为不同交通状况下的路径诱导提供依据。对长沙市路网的实例用矩阵迭代法找出了某停驶时间下任意两小区域之间的最短路径。
| [1] | 胡优. OD调查样本容量分析及抽样矩阵优化研究[D]. 长沙:长沙理工大学, 2007. HU You.Reasearch on Sample Size of OD Survey and Optimization of OD Sample Matrix[D]. Changsha:Changsha University of Science and Technology,2007. |
| [2] | 邵春福.交通规划原理[M]. 北京:中国铁道出版社, 2004. SHAO Chun-fu. Traffic Planning[M]. Beijing: China Railway Publishing House,2004. |
| [3] | 周晶, 徐南荣. 起讫点交通出行分布矩阵的极大似然估计方法[J]. 管理工程学报, 1994, 8(1): 46-51. ZHOU Jing, XU Nan-rong. The Maximizing Likelihood Principle of Estimating Origin-destination Traffic Trip Matrix[J]. Journal of Industrial Engineering and Engineering Management, 1994, 8(1): 46-51. |
| [4] | 段进宇, 缪立新, 江见鲸. 由路段交通流量反估出行 OD 矩阵技术的应用[J]. 清华大学学报: 自然科学版, 2000, 40(6): 123-126. DUAN Jin-yu, MIU Li-xin, JIANG Jian-jing. Application of Entropy Maximization Model for Estimating OD Trip Matrices [J]. Journal of Tsinghua University: Science and Technology Edition, 2000, 40(6): 123-126. |
| [5] | 王炜, 孙俊. 大型交通网络OD矩阵推算方法研究[J]. 东南大学学报: 自然科学版, 1996, 26(6): 47-54. WANG Wei, SUN Jun. Research on Method of Estimating OD Matrices for Large Sized Transportation Network [J]. Journal of Southeast University: Natural Science Edition,1996, 26(6): 47-54. |
| [6] | 董敬欣, 吴建平. 使用浮动车检测 OD矩阵的算法及可靠性分析[J]. 北京交通大学学报: 自然科学版, 2005, 29(3): 73-76. DONG Jing-xin, WU Jian-ping. An Algorithm to Estimate OD Matrix with Probe Vehicle and Its Reliability Analysis[J].Journal of Beijing Jiaotong University: Natural Science Edition, 2005, 29(3): 73-76. |
| [7] | HERMAN R, PRIGOGINE I. A Two-fluid Approach to Town Traffic[J]. |
| [8] | ARDEKANI S, HERMAN R. Urban Network-wide Traffic Variables and Their Relations[J]. |
| [9] | WILLIAMS J C, MAHMASSANI H S, HERMAN R. Sampling Strategies for Two-fluid Model Parameter Estimation in Urban Networks[J]. |
| [10] | HONG S Y, LEE C, CHUNG S B, et al. Analysis of Two-fluid Model Using GPS Data [J]. Journal of the Eastern Asia Society for Transportation Studies, 2005(6): 560-572. |
| [11] | DIXIT V V. Behavioural Foundations of Two-fluid Model for Urban Traffic[J]. |
| [12] | 姚荣涵, 王殿海, 曲昭伟. 基于二流理论的拥挤交通流当量排队长度模型[J]. 东南大学学报: 自然科学版, 2007, 37(3): 521-526. YAO Rong-han, WANG Dian-hai, QU Zhao-wei. Equivalent Queue Length Model for Congested Traffic Stream Based on Two-fluid Theory[J]. Journal of Southeast University: Natural Science Edition, 2007, 37(3): 521-526. |
| [13] | 王殿海, 陈松, 魏强, 等. 基于二流理论的路网宏观交通状态判断模型[J]. 东南大学学报: 自然科学版, 2011, 41(5): 1098-1103. WANG Dian-hai, CHEN Song, WEI Qiang, et al. Discrimination Model for Macroscopic Traffic Condition of Urban Networks Using Two-fluid Theory[J]. Journal of Southeast University: Natural Science Edition, 2011, 41(5): 1098-1103. |
 2015, Vol. 31
2015, Vol. 31
