扩展功能
文章信息
- 张之勇, 郭孜政, 姚磊
- ZHANG Zhi-yong, GUO Zi-zheng, YAO Lei
- 基于云模型的非机动车交通流速度仿真
- Simulation of Traffic Flow Speed of Non-motorized Vehicle Based on Cloud Model
- 公路交通科技, 2015, Vol. 31 (11): 126-131
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (11): 126-131
- 10.3969/j.issn.1002-0268.2015.11.020
-
文章历史
- 收稿日期: 2014-09-09
2. 综合交通运输智能化国家地方联合工程实验室, 四川 成都 610031
2. National-provincial United Engineering Laboratory of Integrated and Intelligent Transportation, Chengdu Sichuan 610031, China
我国是非机动车大国,目前的保有量约为5.51亿辆(截止到2013年底,其中普通自行车社会保有量为3.70亿辆,电动自行车社会保有量为1.81亿辆)[1],并且电动自行车(以下简称电动车)因其环保、节能、费用低廉、便捷的特点受到越来越多的普通市民的青睐。杨金花等[2]认为有效缓解交通供需紧张的出行方式是“显示公共交通系统”加“非机动车或步行”。非机动车己成为人们所关注的环保型交通工具,非机动车交通将在我国长期存在。根据本文试验统计数据,在实际使用中,电动车(包括超标电动车)在非机动车中所占比例已经高于80%,逐渐成为我国非机动车的主体。但是,非机动车安全防护性差,骑行行为不稳定,造成了极大的交通安全隐患。因此,研究非机动车交通问题及对策,对优化城市交通系统、促进社会和谐发展具有重要意义。
目前针对交通流的仿真主要集中在机动车交通流,对非机动车交通流的研究较少或模型复杂。李星星[3]分析了非机动车中普通自行车与电动车的差别,但没有进行实际交通数据检验。潘晓东[4]对普通自行车与电动车个体的车速、加速度等相关参数进行了分析。Z. Zhou 等对非机动车车道的宽度、车流密度和车道利用率之间的关系进行了研究[5]。赵亚龙等[6]结合实例对交叉口应用Vissim软件进行了微观仿真,但主要是针对机动车进行的优化设计。杨晓芳等[7]对混合非机动车交通流用多值元胞自动机模型进行模拟,分析了电动车比例提高对混合非机动车交通流的通行能力的影响。王华东等[8]建立了一种新的非机动车流矢量场微观模型,能准确地实现非机动车的交通特点。
随着电动车在非机动车中所占比例的日渐增高,对非机动车交通流仿真是进行非机动车交通工程设计和制订相关标准的基础。上述研究从不同角度分析了非机动车的相关特性,但较少关注非机动车交通流的仿真。因此本研究拟引入云模型理论与方法对非机动车交通流的速度进行仿真,以期为非机动车交通流的特性分析和研究提供参考依据。
1 机动车交通流基本特征分析非机动车交通流中每个个体的车速具有随机性的特点,从整体分布特征可以较为准确地描述,而每个个体的车速自身又不完全符合分布模型的描述,具备模糊性的特征。在云模型将随机性与模糊性有机结合的前提下,可有效地描述非机动车交通流的整体特点和个体车速的特征。因此在分析非机动车交通流的特征时,可将以往的定性描述或粗略的定量描述变为更为准确、全面的定量描述,为非机动车交通流分析提供更为有效、准确、便捷的数据分析方法。
2 云模型的概念与原理云模型是使用自然语言值表示的某个定性概念Ã与其定量表示之间的不确定性转换模型。设U是一个用精确数值表示的论域(一维的、二维的或多维的),U上对应的定性概念Ã对于论域中的任意一个元素x,都存在一个有稳定倾向的随机数y=uÃ(x),叫做x对概念Ã的确定程度,x在论域上的分布称为云模型,简称云。
云的数字特征用期望Ex、熵En和超熵He来表示,他们反映了定性概念Ã整体上的定量特征。期望在数域空间最能够代表定性概念Ã的点,或者说是这个概念量化的最典型样本点。熵反映定性概念Ã的不确定性,这种不确定性表现在以下方面:
(1)熵反映了在数域空间可以被语言值Ã接受的云滴群的范围大小,即模糊度。
(2)熵还反映了在数域空间的云滴群能够代表这个语言值的概率密度,表示代表定性概念的云滴出现的随机性。
(3)熵还揭示了模糊性和随机型的关联性。超熵是熵的不确定性的度量,即熵的熵。
正态云的普适性在文献[9]中已得到证明。正态分布在自然界中普遍存在,正态云模型是用语言值表示的某个定性概念与其定量表示之间的不确定性转换模型,它主要反映客观世界中事物或人类知识中概念的两种不确定性:模糊性和随机性。正态云模型将这两者完全融合在一起,构成定性和定量相互间的映射,充分表现了正态分布和正态隶属函数的普适性。随机性与模糊性通过熵统一表示,构成了不确定知识的表示模型[10]。
正态云模型的应用十分广泛,如文献[11]利用云模型理论确定了道路交通拥堵状态等级。
3 非机动车交通流车速调查 3.1 试验目的真实地记录非机动车行驶过程中的实时数据,包括基本的交通环境信息、车流状态等。采集数据主要是:道路基本信息(非机动车道宽度、非机动车道交通组织形式、道路断面形式)、交通量(非机动车交通量、普通自行车与电动车比例)、骑行速度。
3.2 试验设备试验设备采用视频监测系统,主要由摄像机(带有摄像功能的佳能A640相机)、三角架等组成,另有皮尺等测量工具。
3.3 试验方法与试验过程
摄像机位置选在被摄路段人行天桥上,摄像范围是远离交叉口一定距离的非机动车道。选择路段长度在50 m以上,路况良好,线路平直,机动车道与非机动车道有隔离设施,没有会引起非机动车流量突然增加或减少的出入口,以得到具有一定代表性的路况信息和非机动车交通流信息。
通过视频可以得到测试时间、非机动车经过特定点的时刻、非机动车流量等基本信息。通过测量工具可以测得非机动车道宽度、测试路段长度。
鉴于成都市的路网特点、道路横断面特征、人行天桥分布情况,并结合施工路段实际情况和视频资料的分析,认为一环路九如村的道路状况和视频采集情况较好,最终选择这个调查点进行了较长时间的视频采集。
选择一环路九如村段为最终调查点的原因有:(1)调查点附近人行天桥上的视频采集点覆盖非机动车道距离较长,可减少系统误差;(2)调查路段与交叉口距离较远,可以保证非机动车从路口到达调查路段时已经进行了充分的加速,处于速度变化较小的行驶阶段,保证数据分析过程中得到的平均速度与实际情况较为接近;(3)该路段有机非隔离带,可尽量减少由于机非混行而造成的影响;(4)距离公交车站较远,不产生由于公交车进出站或者港湾式公交站对非机动车道宽度带来的影响;(5)没有占道停车场,不产生由于机动车停车造成的占用非机动车道的问题;(6)一定距离内没有机动车或非机动车的进出口,如停车场、单位、小区出入口等。
利用视频系统记录所选择路段的非机动车交通流情况,记录地点与时间见表 1,所选择的监测地段具有一定的代表性和典型性。
| 调查路段 | 路段长度/m | 车道宽度/m | 与交叉口距离/m | 电动自行车比例/% | |
| 九如村 | 66.30 | 3.10 | 364 | 第1时段 | 84.38 |
| 第2时段 | 86.77 | ||||
| 第3时段 | 85.90 | ||||
数据采集时间选择为星期四,摄像时间段分别从上午8:56(持续时间51′1″)、9:51(持续时间53′55″)、10:47开始(持续时间47′14″)(以下分别称为第1、第2、第3时段)。剔除在路段中途停车等非正常因素影响的个别对象,各获得有效数据914,809,633 个。对速度样本整理获得不同速度下的频次样本29,24,23 个。
假设非机动车交通流车速频次符合正态分布。用SPSS软件(19.0版)的柯尔莫哥洛夫-斯密尔诺夫检验(简称K-S检验)对试验数据进行分析(见表 2、表 3)。3个时段的渐进显著性均大于0.05,接受假设。故可知在这3个时段的非机动车车速频次符合正态分布,可以使用正态云模型进行分析。
| 时间段 | 频次样本个数 | 均值 | 标准差 | 极小值 | 极大值 |
| 第1时段 | 29 | 31.45 | 44.897 | 1 | 151 |
| 第2时段 | 24 | 33.71 | 42.817 | 1 | 138 |
| 第3时段 | 23 | 27.48 | 35.777 | 1 | 120 |
| 时间段 | 第1时段 | 第2时段 | 第3时段 | |
| 频次样本个数 | 29 | 24 | 23 | |
| 正态参数 | 均值 | 31.45 | 33.71 | 27.48 |
| 标准差 | 44.897 | 42.817 | 35.777 | |
| 绝对值 | 0.249 | 0.252 | 0.276 | |
| 最极端差别 | 正 | 0.246 | 0.252 | 0.276 |
| 负 | -0.249 | -0.222 | -0.230 | |
| K-S检验统计值 | 1.340 | 1.236 | 1.324 | |
| 渐近显著性(双侧)概率 | 0.055 | 0.094 | 0.060 | |
根据逆向云的两种典型计算方法对非机动车交通流车速试验数据进行分析。
算法1:RCG1(xi)
输入:输入N个样本点xi=1,2,…,N。
输出:反映定性概念的数字特征(Ex,En,He)。
算法步骤如下:
(1)根据xi计算定量数据的样本均值X=${1 \over N}\sum\limits_{i = 1}^N {{x_i}} $,样本方差(二阶中心距)c2=${1 \over {N - 1}}{\sum\limits_{i = 1}^N {\left( {{x_i} - \bar X} \right)} ^2}$,样本四阶中心距c4=${1 \over {N - 1}}{\sum\limits_{i = 1}^N {\left( {{x_i} - \bar X} \right)} ^4}$;
(2)计算期望:Ex=X;
(3)根据云滴分布的二阶和四阶中心距的推导结果,求解方程组:
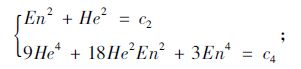
(4)计算熵和超熵:
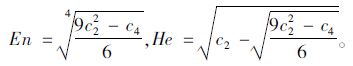
算法2:RCG2(xi)
输入:输入N个样本点xi,i=1,2,…,N。
输出:反映定性概念的数字特征(Ex,En,He)。
算法步骤:
(1)根据xi计算定量数据的样本均值X=${1 \over N}\sum\limits_{i = 1}^N {{x_i}} $,一阶样本绝对中心矩${1 \over N}\sum\limits_{i = 1}^N {} \left| {{x_i} - \bar X} \right|$,样本方差(二阶中心矩)为c2=${1 \over {N - 1}}{\sum\limits_{i = 1}^N {\left( {{x_i} - \bar X} \right)} ^2}$;
(2) 计算期望Ex=X;
(3) 计算熵En=$\sqrt {{\pi \over 2}} {1 \over N}\sum\limits_{i = 1}^N {} \left| {{x_i} - \bar X} \right|$;
(4) 计算超熵He=$\sqrt {{c_2} - E{n^2}} $[10]。
分别以两种算法对第1时段的非机动车交通流速度数据进行处理(表 4、表 5)。
| 测试时间段 | 样本/个 | 均值/(km·h-1) | 样本方差 | 样本四阶中心矩 | 熵 | 超熵 |
| 第1时段 | 914 | 20.379 | 27.232 | 2 441.552 | 5.154 | 0.820 |
| 测试时间段 | 样本/个 | 均值/(km·h-1) | 一阶绝对中心矩 | 样本方差 | 熵 | 超熵 |
| 第1时段 | 914 | 20.379 | 4.127 | 27.232 | 5.172 | 0.691 |
通过算法1和算法2应用正向云发生器可以得到第1时段的两个车速频次云滴图。
正向云发生器FCG(Ex,En,He,N)。
输入:数字特征(Ex,En,He),生成云滴的个数N。
输出:N个云滴x及其隶属度y,也可表示为Drop(xi,yi),i=1,2,…,N。
算法步骤:
(1)生成以En为期望,He2为方差的一个正态随机熵En′i=norm(En,He2);
(2)生成以Ex为期望,Ex′i2为方差的一个正态随机数xi=norm(Ex,En′2);
(3)计算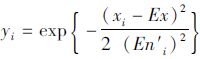 ,具有隶属度yi的xi成为论域U中的1个云滴;
,具有隶属度yi的xi成为论域U中的1个云滴;
(4)重复以上3个步骤,直至生成N个云滴。
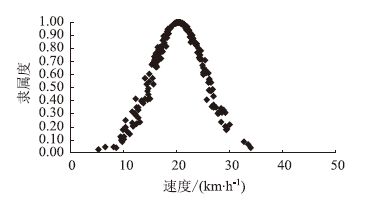
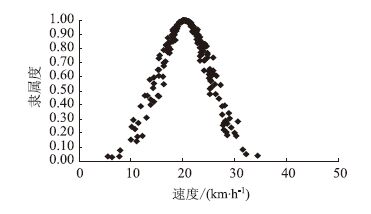
根据九如村调查数据,第1时段根据算法1计算FCG(20.379,5.154,0.820,200),得出云滴图(200个云滴,图 1)。根据算法2计算FCG(20.379,5.172,0.691,200),得出云滴图(200个云滴,图 2)。
|
| 图 1 第1时段仿真云滴图(算法1) Fig. 1 Simulation cloud diagram of period 1 (algorithm 1) |
|
| 图 2 第1时段仿真云滴图(算法2) Fig. 2 Simulation cloud diagram of period 1(algorithm 2) |
图 1和图 2中横坐标为非机动车速度,纵坐标为该速度的隶属度,每个点为1个云滴,表示在该路段出现该速度的隶属度。
根据试验数据可以计算出相应速度的实际隶属度。速度的隶属函数按照正态隶属函数计算。
正态(钟形)隶属函数: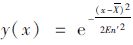 。其中En′为随机熵且En′~N(En,He2)。
。其中En′为随机熵且En′~N(En,He2)。
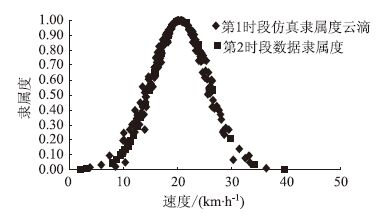
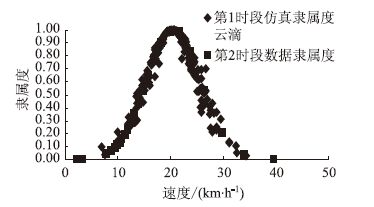
其他两个时段也符合正态分布,但是其均值和方差均与第1时段有差异。因此在图 3~图 6中可以看出,两种算法预测的实际隶属度呈现出不同的吻合度。在云滴图中由于有超熵的存在而使这种差异(即随机性)在一定时间范围内保持了较高的吻合度。但随着时间的推移,误差明显增大(表 6)。还可以看出,不在预测范围内的数据依然在预测云滴图边界附近(绝对误差较小)。
|
| 图 3 第2时段数据与云滴图(算法1)比较 Fig. 3 Comparison of data of period 2 and cloud diagram (algorithm 1) |
|
| 图 4 第2时段数据与云滴图(算法2)比较 Fig. 4 Comparison of data of period 2 and cloud diagram (algorithm 2) |
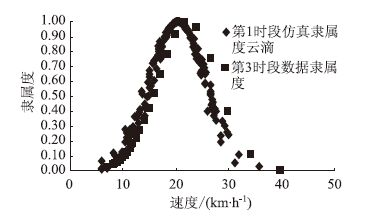
|
| 图 5 第3时段数据与云滴图(算法1)比较 Fig. 5 Comparison of data of period 3 and cloud diagram (algorithm 1) |
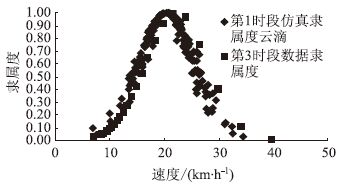
|
| 图 6 第3时段数据与云滴图(算法2)比较 Fig. 6 Comparison of data of period 3 and cloud diagram (algorithm 2) |
根据仿真模型和试验数据之间的关系,可以得出仿真模型参数的基本含义:
(1)数学期望为样本均值,是非机动车交通流整体快慢的直观反映。
(2)熵反映了云滴群的范围大小,即模糊度。熵还反映了云滴群能够代表这个语言值的概率密度,表示代表定性概念的云滴出现的随机性;熵还揭示了模糊性和随机型的关联性。熵表示了非机动车速度的集中性。
(3)超熵是熵的不确定性的度量,即熵的熵。超熵决定了速度仿真云的厚度及该路段速度的不确定性程度。
期望、熵和超熵的含义见图 7。
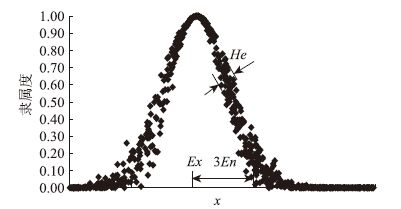
|
| 图 7 期望、熵和超熵的含义 Fig. 7 Meanings of Ex,En and He |
(1) 仿真模型中的期望、熵和超熵的含义分别为非机动车速度的均值、方差和二阶中心矩,这些参数的确定相对简单易行。两种经典算法的预测数据在本试验中没有明显差异。
(2) 利用云模型对非机动车交通流路段速度参数进行仿真与实际情况吻合较好,是一种较好的非机动车交通流路段速度参数的仿真算法。
(3)随着与原始数据时间差距的增大,仿真结果误差明显增大。但仿真结果的绝对误差值较小,因此对非机动车速度的短时间仿真效果更优。
由于云模型可以较好地描述非机动车交通流的随机性和模糊性,仿真结果更符合实际情况,可以为非机动车交通流的研究,尤其是电动车安全的研究提供参考。
但本文在分析过程中,对普通自行车与电动车的速度差异并没有凸显出来,也没有对不同比例条件下的速度变化情况进行分析,这将在今后进一步研究。
| [1] | 胡俊超. 新华网[EB/OL]. [2014/04/27]. http://news.xinhuanet.com/2014-04/27/c_1110429434.htm. HU Jun-chao. Xinhua Net[EB/OL].[2014/04/27]. http://news.xinhuanet.com/2014-04/27/c_1110429434.htm. |
| [2] | 杨金花,季令. 城市交通系统的非机动车交通问题及对策[J].铁道运输与经济, 2006,28(5):14-16. YANG Jin-hua, JI Ling. Problems and Countermeasures on Non-motorised Vehicle Traffic of Urban Transit System[J]. Railway Transport and Economy, 2006,28(5):14-16. |
| [3] | 李星星,马健霄,徐佳逸. 非机动车跟驰模型的研究[J]. 交通运输工程与信息学报, 2012,10(1):115-120. LI Xing-xing, MA Jian-xiao, XU Jia-yi. Study on Non-motorized Vehicle-following Model[J]. Journal of Transportation Engineering and Information, 2012,10(1):115-120. |
| [4] | 潘晓东,赵晓翠,杨轸,等. 非机动车骑行行为实验研究[J].长沙交通学院学报,2008,24(4):62-71. PAN Xiao-dong, ZHAO Xiao-cui, YANG Zhen, et al. The Experimental Research on Riding Behavior of Non-motorized Vehicle[J]. Journal of Changsha Communications University, 2008,24(4):62-71. |
| [5] | ZHOU Zhao,WANG Jian-bo,HE Cao,et al. The Relationship between Non-Motor Vehicle Lane's Utilization and Width and Other Factors[J]. Applied Mechanics & Materials, 2014, 505-506:827-831. |
| [6] | 赵亚龙,王喜富,李宏峰. 交叉口混合交通流仿真设计及应用[J]. 交通信息与安全,2012,30(5):125-129. ZHAO Ya-long, WANG Xi-fu, LI Hong-feng. Design and Application of Mixed Traffic Flows Simulation in Intersection[J]. Journal of Transportation Information and Safety, 2012,30(5):125-129. |
| [7] | 杨晓芳,牛兆雨,王建蓉. 基于多值元胞机的混合非机动车通行能力研究[J].系统仿真学报,2012,24(12):2577-2581. YANG Xiao-fang, NIU Zhao-yu, WANG Jian-rong. Mixed Non-motorized Traffic Flow Capacity Based on Multi-value Cellular Automata Model[J]. Journal of System Simulation, 2012,24(12):2577-2581. |
| [8] | 王华东,吴铁军. 一种新的交通流矢量场微观模型[J].中国公路学报, 2003, 16(2): 99-102. WANG Hua-dong, WU Tie-jun. New Vector Field Microcosmic Model for Traffic Flow[J]. China Journal of Highway and Transport, 2003, 16(2): 99-102. |
| [9] | 李德毅,刘常昱. 论正态云模型的普适性[J]. 中国工程科学, 2004, 6(8):28-34. LI De-yi, LIU Chang-yu. Study on the Universality of the Normal Cloud Model[J]. Engineering Science, 2004, 6(8):28-34. |
| [10] | 刘常昱,李德毅,潘莉莉. 基于云模型的不确定性知识表示[J]. 计算机工程与应用, 2004, 40 (2):32-35. LIU Chang-yu, LI De-yi, PAN Li-li. Uncertain Knowledge Representation Based on Cloud Model[J]. Computer Engineering and Applications, 2004,40(2):32-35. |
| [11] | 高雅隽,许伦辉. 基于云模型的交通状态评价系统及其应用[J].公路交通科技, 2013, 30 (11):124-130. GAO Ya-jun, XU Lun-hui. Traffic State Evaluation System Based on Cloud Model and Its Application[J]. Journal of Highway and Transportation Research and Development, 2013, 30 (11):124-130. |
 2015, Vol. 31
2015, Vol. 31
