扩展功能
文章信息
- 卢维科, 刘澜, 冯伟
- LU Wei-ke, LIU Lan, FENG Wei
- 基于相邻相位合作博弈的单信号交叉口实时滚动优化建模和仿真
- Modelling and Simulation of Single Signal Intersection Real-time Rolling Optimization Based on Adjacent Phases Cooperation Game
- 公路交通科技, 2015, Vol. 31 (11): 120-125,131
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (11): 120-125,131
- 10.3969/j.issn.1002-0268.2015.11.019
-
文章历史
- 收稿日期: 2014-12-14
交叉路口是城市道路网络交通中各向交通流汇聚交错的地点,对它的交通信号控制是城市交通控制系统的核心[1]。单交叉路口交通信号控制配时方案的设计与优化,是实现干道协调控制系统和区域协调控制系统的基础[2]。要实现未来城市交通控制的智能化和自动化,单交叉口的信号控制与优化显得极为重要。单交叉口信号控制配时方法按相序变化分为不变相序控制和可变相序控制两种。其中可变相序可以通过提取道路数据选取最有价值通行相位,但是改变交叉口的相序没有考虑驾驶员停车按相位顺序等待绿灯的习惯,而且由于相位切换造成的处理冲突的时间变长。本文研究不变相序控制主要原因有两点: (1)不变相位控制符合驾驶员停车等待通行的习惯; (2)不变相序可以成为滚动优化的基础条件。不变相序控制的配时主要包括Webster配时方法、冲突点法、估算法、临界车道法和感应控制法。
Webster配时方法、冲突点法、估算法、临界车道法这4种方法都属于不变相序定周期控制方法的范畴,这类配时方法虽然在某一交通条件下控制效果良好,但是当交通条件发生变化时,这类方法因受固定配时方案的约束,无法充分有效利用和分配绿灯资源。
常规感应控制没有固定的周期,通过在交叉口入口道上放置检测器,如果检测器检测有车辆通过则增加绿灯时间,但是没有考虑到相位之间的矛盾,增加绿灯时间可能会造成其他相位平均停车时间增大。
本文提出的控制也是一种感应控制,与常规感应控制不同的是,本文在计算执行绿灯时间时考虑了对下一绿灯相位的影响,将执行绿灯的相位和下一相位作为一个整体,把在时间窗内使得整体平均停车时间最低的时间作为执行绿灯时间,以此为基础,每次相位切换选择将要执行绿灯的相位和下一相位为对象,求解出最优绿灯时间,从而达到让所有相位的绿灯时间最优的目的。
1 车辆平均停车时间特性分析与建模思想 1.1 平均车辆停车时间的计算及特性分析设 θ∈(1,2,3,4) 为信号交叉口的4个相位, r∈(1,2) 为每一相位所对应的两个入口道组,在t时刻,每个进口道的到达率为 qθr(t)(r∈1,2)。 假设信号交叉口在tf时刻发生切换相位,切换后执行绿灯的相位执行时间为tg。用Qθr(tf)表示tf末θ相位的停车数量。用Sθr(tf)表示tf末θ相位停车所产生的总时间,则tg时刻某相位的平均车辆停车时间计算方式与特性为:
(1)如某相位θ在tf到tf+tg是红灯,在tf+tg时刻,平均每辆车的停车时间为:
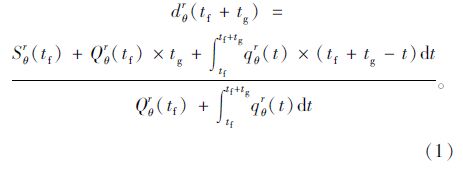
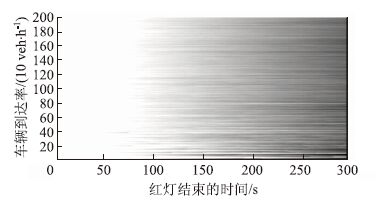
用MATLAB软件生成了到达车辆在1~2 000 veh/h之间的符合泊松分布的随机车辆,绘制了绿灯时间在0~300 s之间逐渐增大过程中执行红灯相位车辆平均停车时间变化图(图 1)。
|
| 图 1 持续红灯时间在0~300 s之间不同流量的车辆平均停车时间变化图 Fig. 1 Changes of vehicle average parking time in different volumes during red light time from 0 s to 300 s |
从图 1可知,执行红灯的相位的车辆平均停车时间随绿灯时间tg的增大而增多。
(2)如某相位θ在tf到tf+tg是绿灯,在tf+tg时刻,令tf时刻红灯产生的停车数全部消散完,N*为绿灯期间等待前面排队车启动的车辆数,它在绿灯开启时到启动加速时的时间产生的停车时间为ξi。则产生的总停车时间为:
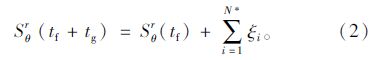
通过的车辆总数为:
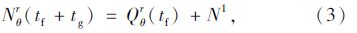
平均每辆车的停车时间为:
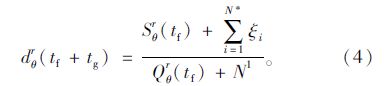
绿灯开始后, Sθr(tf),Qθr(tf) 为常数。当绿灯时间tg大于排队车辆消散时间t0时,由于消散过程产生的总停车时间 $\sum\limits_{i = 1}^{{N^*}} {{\xi _i}} $ 变为常数,绿灯期间通过车辆数N1开始变大。所以当绿灯时间tg大于排队车辆消散时间t0时,车辆的平均停车时间随时间的增大而减少。
1.2 建模思想根据以上分析,两个相邻的相位θ0和θ1(其中θ0相位为tf末将要执行绿灯的相位,θ1为θ0的下一相位)总是存在一种矛盾。随着绿灯时间的增大,执行绿灯θ0相位的平均车辆停车时间在减少,而执行红灯θ1相位的平均车辆停车时间在增加。所以tg绿灯时间越长, dθ0r(tf+tg) 越短,对θ0越有利,但tg绿灯时间越长, dθ1r(tf+tg) 越长,对θ1 越不利。这种关系可以描述成θ0和θ1对tg绿灯资源的博弈,但同时要求整个由θ0和θ1组成的联盟效益最高,这种相互竞争又互相合作的关系可以描述为合作博弈。
合作博弈论又称联盟博弈论,由于在解决世界上各类资源共享问题和避免冲突方面有独到的方法,近年来在运筹学中的地位与日俱增[3]。合作博弈有3个要素:局中人、参与者的策略集合和价值函数[4, 5, 6, 7, 8, 9]。
结合以上分析,局中人集合 S={θ0,θ1}, 参与者的策略集合T为tg∈[g0,g1] ,对θ0来说,tg=g1时,即绿灯时间达到策略集合的上限时,θ0相位将获得最大收益,即θ0的平均停车时间最小,此时的收益为θ0的目标收益dθ0r(tf+g1)。那么在时间窗 tg∈[g0,g1] 内,θ0的收益损失为 dθ0r(tf+tg)-dθ0r(tf+g1),tg 时刻的相对目标收益损失率为:
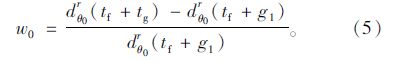
对θ1来说,tg=g0时,即绿灯时间达到策略集合的下限时,θ1相位将获得最大收益,即θ1的平均停车时间最小,此时的收益为θ1的目标收益 dθ1r(tf+g0)。 那么在时间窗 tg∈[g0,g1] 内,θ1的收益损失为 dθ1r(tf+tg)-dθ1r(tf+g0),tg 时刻的相对目标收益损失率为:
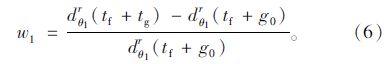
要使由θ0和θ1组成的联盟效益最高,则使得局中人相对目标收益的损失率之和最小即可,即在时间窗[g0,g1]内,找出使z=w0+w1最小的时间点tg,意味着此时合作联盟效益最大。
2 模型建立与滚动优化2.1 建立模型
根据参数分析和建模思想建立如下模型:
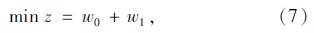
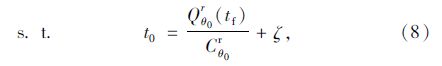
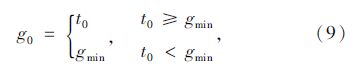

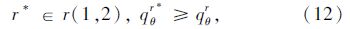
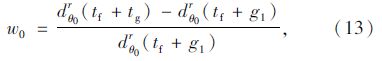
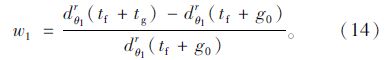
为了使局中人θ0和θ1在合作博弈中的{θ0,θ1}联盟效益最高,所以选取式(7)为目标函数。约束条件式(8)中,Cθ0r为r车道组的饱和流量,ζ为车辆启动时间,这个约束条件是为了保证排队车辆都可以消散。约束条件式(9)作用在于规定g0为决策变量绿灯时间tg下限,当车队消散时间比最小绿灯时间gmin小时取gmin,当消散时间大于等于gmin时取消散时间。式(10)规定g1为决策变量绿灯时间tg的上限,目的在于缓解滚动优化过程中绿灯时间过长而造成其他未参加相位停车过多的现象。约束条件(11)为决策变量tg的范围。约束条件(12)表示选择每一相位中最大到达率的入口道作为研究对象,r*为θ相位中最大到达率的入口道,qθr*≥qθr表示选取r*的方法。式(13)为执行绿灯相位tg时刻相对目标收益的损失率。式(14)为执行红灯相位tg时刻相对目标收益的损失率。
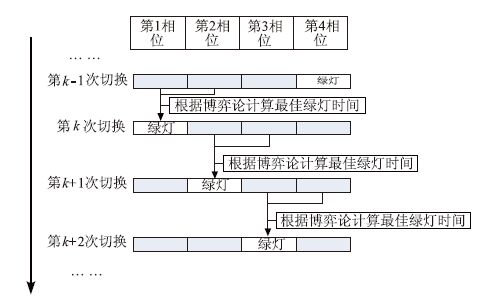
2.2 滚动优化本文建立的单交叉口滚动控制是按照相位顺序依次进行滚动从而求出每次绿灯时间的控制模式[10]。主要思想是在信号灯第k次相位切换时,把将要执行绿灯的相位和此相位的下一相位视作参加合作博弈联盟的两名局中人,以整个联盟平均车辆停车时间的相对目标收益损失率之和为目标函数,将要执行的绿灯时间作为两名局中人的决策变量,在对应的绿灯时间范围内,求出使联盟平均车辆停车时间的最小绿灯时间,总体控制流程如图 2所示。
|
| 图 2 滚动优化图 Fig. 2 Rolling optimization process |
根据停车时间计算公式,令函数g(t)为t时刻到达率下的停车时间的函数:
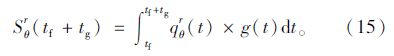
利用定积分原理
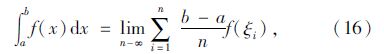
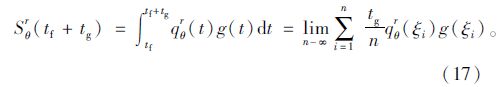
本文假设用一台频率为1(即每s照1次照片)的照相机悬停在交叉口上方进行拍照,那么可以将时间段tg划分成tg个微小的时间区间,则每个时间序列为1 s,那显然在任意一个微小的时间序列ξi=1里,qθr(ξi)为第i秒拍摄的图片上某进口道的停车数量,此时用Mi表示,那么g(ξi)为这个时间序列的停车时间,此处可以近似看成1 s。
综上所述,
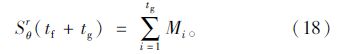
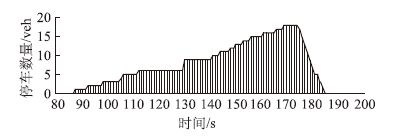
基于VISSIM二次开发,利用上面提出的方法提取了某进口道在80~184 s之间从遇到红灯到绿灯后消散的车辆数,见图 3。
|
| 图 3 某进口道在80~200 s之间每秒停车数量统计图 Fig. 3 Parking quantity statistics of an entrance lane per second from 80 s to 200 s |
在80~200 s之间,此车道红灯产生的停车总时间为85~175 s的停车时间累计和,等于856 s,从图 3看即为85~175 s的阴影面积。175 s时排队开始消散,红灯排队车数为18 veh。平均停车时间为47.56 s。
3.2 排队消散过程中车辆等待时间的计算根据信号交叉口的间断流理论,当信号转为绿灯时,车队开始进入交叉口,第1辆车的车头时距比较长,因为第1辆车的驾驶员最先看到绿灯信号,然后产生反应,使车辆进入交叉口。第2车头时距是第1辆和第2辆的保险杠通过标线的时间间隔,这个值比较小,因为第2辆车的驾驶员对红灯的反应几乎重合,第3车头时距比第2车头时距更小,以此类推。最后(通常在第4和第6时距之间),各车辆到达观察标线均已充分加速。假设在排队的车辆只有紧靠它的前面的车辆启动才可以启动,且每辆车的启动时间相同,每名驾驶员的反应时间相同,启动损失时间加反应时间为常数A。所以对于一个排队的驾驶员序列,设ξi为第i名驾驶员的停车等待时间,则存在以下关系:

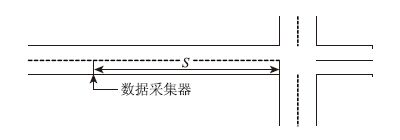
为了预测有可能在绿灯时间tg内通过交叉口的车辆及其时间,假设在进口道处行驶的车辆车速变化波动不大,即认为它是匀速,在离停车线S(现取600 s)处放置一个数据检测器,如图 4所示。数据检测器可以记录车辆vehiclei通过检测器的时刻ti和车辆速度vi,那么可以推算出vehiclei到达停车线的时刻为[11, 12]:

|
| 图 4 检测器的放置 Fig. 4 Place schematic detector |
当tia≥tf+tg时,vehiclei没有在绿灯时间内到达交叉口,如果θ相位在tf到tf+tg内执行绿灯,那么当tf≤tai≤tf+tg时,可以认为vehiclei可以在绿灯时间tg通过交叉口。如果θ相位在tf到tf+tg内执行红灯,那么当tf≤tia≤tf+tg时,可以认为vehiclei参与了排队,结合式(20),则vehiclei在tf+tg末的停车时间可以表示为:
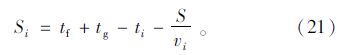
由上述所建模型可知,此模型是关于绿灯时间tg的整数非线性规划问题,而且tg的可行解解集有限,因此用全枚举法对每个可行解进行罗列,从中提取出最优解来。
Step1:通过检测数据罗列出每个可行解下的目标函数值。
Step2:比较每个可行解的目标函数,求出最优解。
4 仿真试验 4.1 滚动优化实现的总流程VISSIM是交通微观仿真软件,本文用VISSIM的com接口与Excel VBA编辑器搭建仿真平台[13, 14, 15],对相邻相位合作博弈的滚动优化模型进行仿真[16],总体模型计算及仿真流程如图 5所示。
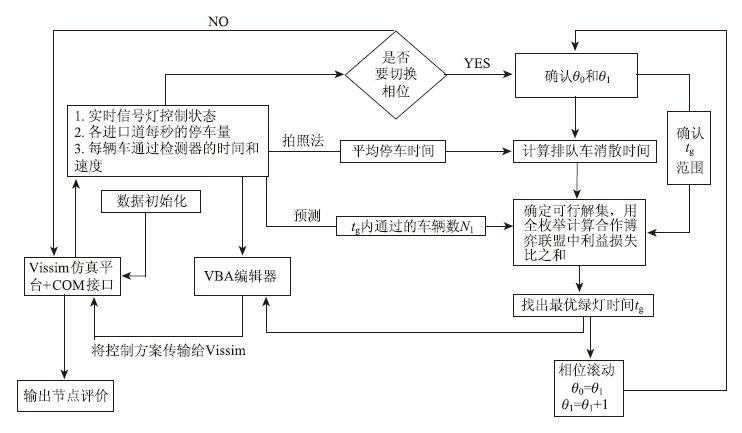
|
| 图 5 基于相邻相位合作博弈的滚动控制仿真流程图 Fig. 5 Flowchart of simulating rolling control based on cooperation game during adjacent phases |
为了对基于相邻相位合作博弈论滚动控制的特性进行对比,本文选取一个四 相位信号控制交叉口进行仿真,如图 6所示。感应控制方法中,线圈检测器布置在进口道上游距离停止线30 m处,最大绿灯时间50 s,最小绿灯时间20 s。
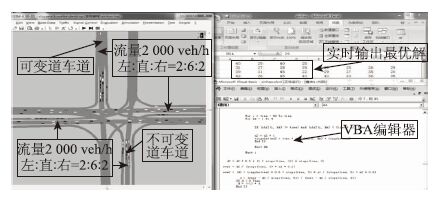
|
| 图 6 基于相邻相位合作博弈的滚动控制仿真过程截图 Fig. 6 Screenshot of simulating rolling control based on cooperation game during adjacent phases |
选择每200 s对节点进行一次评价,评价参数为节点平均车辆延误和节点平均排队长度。
试验结果见图 7和图 8。图 7表明,当前入口道流量下,基于博弈论的滚动控制节点平均延误稍优于感应控制。
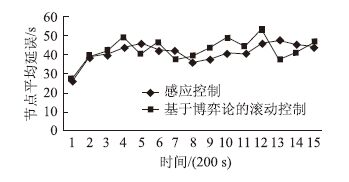
|
| 图 7 每200 s节点平均延误对比图 Fig. 7 Contrast curves of node average delay per 200 s |
|
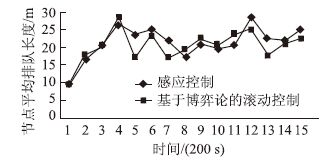
| 图 8 每200 s节点平均排队长对比图 Fig. 8 Contrast curves of node average queue length per 200 s |
图 8表明,当前入口道流量下,基于博弈论的滚动控制节点平均排队长度稍优于感应控制。
通过节点评价,对所有时间序列取平均值,感应控制每200 s节点平均延误为41 s、每200 s节点平均排队长度为21 m,基于相邻相位合作博弈的滚动控制每200 s节点平均延误为38 s,比感应控制少3 s;每200 s节点平均排队长度为19 m,比感应控制少2 m。虽然在有的时间序列里,基于相邻相位合作博弈的滚动控制相关评价参数会稍微超过感应控制,但是超出的差值较小。
综合以上分析,在此流量下,基于相邻相位合作博弈的滚动控制优于感应控制。
5 结论首先建立了基于相邻相位合作博弈的滚动优化模型,并通过搭建仿真平台将其实现。对比同等条件下的感应控制,得到了良好的控制效果,证明基于相邻相位合作博弈的滚动优化模型具有可行性。论证了在信号交叉口中绿灯相位与红灯相位间存在对绿灯资源的博弈,并将合作博弈论运用于信号配时当中。其次提出了基于拍照法采集和计算停车时间的方法,同时利用VISSIM软件和VBA搭建的仿真平台求解模型并对其仿真。本文存在不足之处在于对绿灯时间内将要通过交叉口或到达交叉口的车辆预测方法有待改进,同时对模型中的相关常数参数还需进行校正。下一步工作包括:(1)改进预测和数据采集方法,提高准确性。(2)研究将4个相位同时参加合作博弈的滚动优化。
| [1] | 罗霞,刘澜. 交通管理控制[M]. 北京:人民交通出版社,2008:141-200. LUO Xia, LIU Lan. Traffic Management and Control [M].Beijing: China Communications Press,2008:141-120. |
| [2] | 刘澜,卢维科,尹俊淞.城市交通拥挤对策新解[J].交通运输工程与信息学报,2014,12 (4):1-7. LIU Lan, LU Wei-ke,YIN Jun-song. New Interpretation on Urban Traffic Congestion Countermeasures[J]. Journal of Transportation Engineering and Information,2014,12(4):1-7. |
| [3] | 蒋鹏飞. 合作博弈解及其应用研究[D]. 济南:山东大学,2007. JIANG Peng-fei. Research on Solution and Application of Cooperation Games [D].Jinan: Shandong Univercity,2007. |
| [4] | 李保明.效用函数与纳什均衡[J].Mathematics in Economics,2000,17(4):4-5. LI Bao-ming. Utility Function and Nash Equilibrium[J]. Mathematics in Economics, 2000,17(4):4-5. |
| [5] | ZHANG Guo-peng,YANG Kun,HU Qing-song,et al.Bargaining Game Theoretic Framework for Stimulating Cooperation in Wireless Cooperative Multicast Networks [J]. |
| [6] | 李迪.基于博弈论的城市交通管控策略与仿真研究[D].长春:吉林大学.2013. LI Di. Research of Urban Traffic Management Strategy and Simulation Based on Game Theory[D].Changchun: Jilin Univercity,2013. |
| [7] | 蔡永泉,孙科.基于重复博弈参与者有权重的秘密共享方案[J]. 计算机工程, 2012, 38(18):120-122. CAI Yong-quan,SUN Ke. Secret Sharing Scheme with Weighted Participants Based on Repeated Games[J]. Computer Engineering,2012,38(18):120-122. |
| [8] | LIN S, DE SCHUTTER B, XI Y. A Simplified Macroscopic Urban Traffic Network Model for Model-based Predictive Control[C]//Proceedings of IEEE IFAC Symposium Control Transportation Systems. Redondo Beach: IEEE, 2009: 286-291. |
| [9] | LIN S, DE SCHUTTER B, XI Y, et al. Efficient Network-wide Model-based Predictive Control for Urban Traffic Networks[J]. |
| [10] | 杨海荣,罗大庸. 交叉口信号实时滚动优化模型及算法[J].控制与决策, 2014,29(4):645-651. YANG Hai-rong, LUO Da-yong. Real-time Rolling Horizon Optimization of Intersection Signal Model[J]. Control and Decision,2014,29(4) :645-651. |
| [11] | 张存保,冉斌,梅朝辉,等. 车路协同下道路交叉口信号控制优化方法[J].交通运输系统工程与信息,2013,13(3):1-5. ZHANG Cun-bao,RAN Bin,MEI Chao-hui,et al. An Optimization Method of Traffic Signal Control Based on Cooperative Vehicle Infrastructure System[J]. Journal of Transportation Systems Engineering and Information Technology, 2013,13(3):1-5. |
| [12] | 邹智军.车路集成系统探测车数据采集仿真研究[J].系统仿真学报, 2009, 21(18):5955-5960. ZOU Zhi-jun. Study on Vehicle-infrastructure Integration Probe Data Collection Simulation [J]. Journal of System Simulation, 2009, 21(18) :5955-5960. |
| [13] | PTV Planung Transport Verkehr AG. VISSIM 5.20-10 COM Interface Manual[R]. [S. l.] : PTV Planung Transport Verkehr AG, 2010. |
| [14] | WIEDEMANN R,REITER U. Microscopic Traffic Simulation: The Simulation System Mission,Background and Actual State[R].Brussels: [s.n.],1992. |
| [15] | 卢守峰,韦钦平,沈文, 等. 集成 VISSIM、Excel VBA和MATLAB的仿真平台研究[J].交通运输系统工程与信息, 2012,12(4):43-49. LU Shou-feng, WEI Qin-ping, SHEN Wen, et al. Integrated Simulation Platform of VISSIM, Excel VBA, MATLAB [J]. Journal of Transportation Systems Engineering and Information Technology, 2012,12(4): 43-49. |
| [16] | 夏新海. 面向城市自适应交通信号控制的强化学习方法研究[D]. 广州:华南理工大学,2013. XIA Xin-hai. Study of Reinforcement Learning towards Urban Self-adaptive Traffic Signal Control Environment[D]. Guangzhou: South China University of Technology, 2013. |
 2015, Vol. 31
2015, Vol. 31
