公路交通科技  2015, Vol. 31 Issue (11): 107-112,119

扩展功能

文章信息

成卫, 李冰, 雷建明, 刘荣贵
CHENG Wei, LI Bing, LEI Jian-ming, LIU Rong-gui
远引调头对下游交叉口通行能力的影响
Influence of U-turn on Capacity of Downstream Intersection
公路交通科技, 2015, Vol. 31 (11): 107-112,119
Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (11): 107-112,119
10.3969/j.issn.1002-0268.2015.11.017

文章历史

收稿日期: 2015-01-04
引用本文 0
成卫, 李冰, 雷建明, 刘荣贵. 远引调头对下游交叉口通行能力的影响[J]. 公路交通科技, 2015, Vol. 31 (11): 107-112,119.
CHENG Wei, LI Bing, LEI Jian-ming, LIU Rong-gui. Influence of U-turn on Capacity of Downstream Intersection[J]. Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (11): 107-112,119.
远引调头对下游交叉口通行能力的影响
成卫1 , 李冰2, 雷建明3, 刘荣贵1    
1. 昆明理工大学 云南省高校智能交通系统工程研究中心, 云南 昆明 650093;
2. 昆明理工大学, 交通工程学院, 云南 昆明 650093;
3. 玉溪市公安局交通警察支队, 云南 玉溪 653100
收稿日期: 2015-01-04
基金项目: 国家自然科学基金项目(61364019).
作者简介: 成卫(1972-),男,云南宣威人,教授,博士生导师.
摘要: 为了准确分析在主干路上设置中央隔离栏以后,支路原有直接左转的车辆对下游交叉口的影响,以交通流理论为基础,以交叉口通行能力为评价指标,建立了车头时距与通行能力之间的关系模型。研究结果表明:对于信号交叉口,当调头流量的百分比为21%,调头车辆的修正系数为0.95,即左转专用车道的通行能力降低了5%时,尽管交叉口通行能力有所降低,但是远引调头的运行效率将比直接左转的高,此时设置中央隔离栏对提高主干路交通运行效率具有积极意义;对于无信号控制交叉口,在主干路流量小于850 pcu/h时,不同主干路车头时距对应的支路的通行能力比较接近,当主干路流量大于1 250 pcu/h时,不同的主干路车头时距对应的支路的通行能力差异较大,即不同的主干路车头时距对支路的通行能影响较大。
关键词: 交通工程     通行能力     回归分析     中央隔离     远引调头    
Influence of U-turn on Capacity of Downstream Intersection
CHENG Wei1 , LI Bing2, LEI Jian-ming3, LIU Rong-gui1     
1. ITS Center of Higher Institutions in Yunnan Province, Kunming University of Science and Technology, Kunming Yunnan 650093, China;
2. School of Transportation Engineering, Kunming University of Science and Technology, Kunming Yunnan 650093, China;
3. Traffic Police Detachment of Yuxi Public Security Bureau, Yuxi Yunnan 653100, China
Abstract: In order to accurately analyze the impact of direct left turn traffic of branch road on downstream intersection after setting central isolation fence in arterial road, the relationship model between time headway and capacity is built based on traffic flow theory and taking capacity of intersection as evaluation indicator. The research result shows that (1) for signalized intersection, when the percentage of U-turn vehicles is 21%, the correction factor of U-turn vehicles is 0.95, i.e., the capacity of left turn lane is reduced by 5%, although the capacity of intersection has decreased, the U-turn traffic has higher efficiency than the direct left turn traffic, so setting central isolation fence has positive significance to improve efficiency of arterial road; (2) for non-signalized intersection, when traffic volume in arterial road is less than 850 pcu/h, the different time headway of arterial road corresponding to the capacity of branch road is no significant difference, when the arterial road traffic volume is greater than 1 250 pcu/h, the different time headway of arterial road corresponding to the capacity of branch road is obviously different, i.e., the different headway of arterial road traffic has a larger effect on the capacity of branch road.
Key words: traffic engineering     capacity     regression analysis     central isolation     U-turn    
 0 引言

在主干路上设置中央隔离栏以后，支路处原有进行直接左转的车辆只能右转到下游交叉口进行远引调头完成出行[1]。对于下游交叉口来说，这些转移的交通流量会打破其原有的交通运行状态，对交叉口的通行能力产生影响。转移交通量的远引调头可以分为右转到下游中央隔离栏开口处远引调头和右转到下游交叉口远引调头[2]。第1种情况由于受到交织段长队、隔离栏开口位置等因素的制约，本文不做分析。本文将对第2种情况进行分析研究。而第2种情况又可以分为右转到下游信号交叉口远引调头和右转到下游无信号交叉口处远引调头。

1 对信号控制交叉口的影响

上游支路开口处安装中央隔离栏之后，直接左转的车辆转移到下游交叉口，在信号交叉口处，远引调头的车辆就会进入左转专用车道。因此，信号交叉口远引调头的通行能力取决于内侧左转专用车道的通行能力[3]，从这个意义上说，转移交通量对信号交叉口通行能力的影响，即调头车辆对左转专用车道通行能力的影响。由于受研究条件和时间的限制，本文主要选择在左转专用车道和相位的条件下，远引调头车辆对信号交叉口通行能力的影响。

1.1 信号交叉口饱和流率计算

在现有的信号交叉口通行能力研究成果中，最广泛的当属美国《道路通行能力手册》中的饱和流率模型。但由于交通特性、交叉口基础设施等条件的限制，该模型中饱和流率受到进口道车道组中车道数量及其宽度、道路坡度、大型车辆比例、转向车辆比例(包括左转车辆和右转车辆)等因素的制约，该方法并不常用。此外，《道路通行能力手册》还介绍了通过实地调查直接测量饱和流率的方法，该方法比理论计算的方法更精确，且不用进行修正[4]。其简便之处在于在现场调查时只需调查平均饱和车头时距。其方法为：当绿灯开始时，记录进入交叉口的所有车辆及其各自对应的时刻。为使计算出的平均饱和车头时距更加准确，通常选取车流运行状态相对稳定的时段计算平均车头时距。一般情况下，当第4辆车进入交叉口时，交通状态已经趋于相对稳定状态。因此，选择进入交叉口的第4辆车所对应的时刻以及最后一辆进入交叉口的车辆及其所对应的时刻计算饱和车头时距，然后，通过饱和车头时距计算饱和流率。饱和车头时距和饱和流率之间的关系为：

式中，s为饱和流率；h为平均饱和车头时距，h=${{{t_n} - {t_{n - 4}}} \over {n - 4}}$，式中n为总观测车辆数，tn，tn－4分别为第n辆、第n－4辆车进入交叉口的时刻。

在求解了饱和流率的基础上，一条车道或一个车道组的通行能力为：

式中，ci为车道(组)i的通行能力；si为车道(组)i的饱和流率；${{{g_i}} \over c}$为有效绿灯时间与信号周期的比值，即绿信比。

1.2 调头车辆对车头时距的影响

在本节的概述中提到，远引调头车辆对信号交叉口通行能力的影响其实就是调头车辆对左转专用车道通行能力的影响。根据式(1)和式(2)，可以通过研究调头车辆对平均饱和车头时距的影响，间接分析远引调头对信号交叉口通行能力的影响。

采用实地调查计算平均饱和车头时距的方法。当信号灯启亮且通过交叉口约4辆车以后，车辆放行的状态就会趋于稳定，平均车头时距也会达到稳定值[5]。但是，由于没有专用的调头车道，左转车辆将与右转车辆共用一条车道，在这样的情况下，由于受到调头车辆的影响，车辆的运行状态将很难趋于稳定，导致在调查过程中很难得到饱和的平均车头时距[6]。实际调查得到的数据如表 1所示，当调头车辆的比例较大时，车头时距并没有趋于稳定值。

表 1 不同位置对应的平均车头时距 Tab. 1 Average time headways corresponding to different locations
调头车辆比例/% 队列位置 平均车头时距/s
Pu>50 1 2.4
2 3.0
3 2.5
4 2.6
5 2.4
6 2.8
7 2.4
8 2.6
0＜Pu＜50 1 2.5
2 2.6
3 2.7
4 2.4
5 2.3
6 2.0
7 2.1
8 1.8
Pu=0 1 2.9
2 2.7
3 2.4
4 2.1
5 2.0
6 1.9
7 1.8
8 2.1
 注：Pu为掉头车辆的比例，队列位置为调头车辆所在该队列的顺序。
表选项

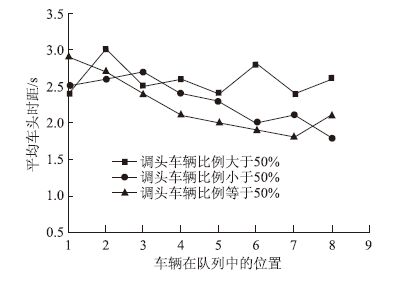
根据表 1的数据可以得到不同调头比例情况下，队列中平均车头时距的曲线变化示意图(图 1)。从表 1和图 1可知，由于调头车流对左转车流会产生一定的影响，导致左转专用道的车头时距没有趋于一个相对稳定值。为了能够定量分析调头车流对左转专用道饱和流率的影响，在计算左转专用车道饱和流率时，针对调头车流引入一个修正系数，其大小可以直观反映调头车流对左转专用车道饱和流率的影响。

图 1 不同比率调头车对应的车头时距 Fig. 1 ifferent ratios of U-turn vehicles corresponding to time headways
图选项

引入的调头车流修正系数并不是不受限制的。相反，为了体现其科学性和合理性，需要考虑以下因素[7]：

(1)所选取的信号交叉口须有左转专用车道；

(2)须有与左转专用车道相对应的左转专用相位，以消除其他车流对左转饱和流率的影响；

(3)左转专用车道上须有不同比例的调头车辆；

(4)交叉口处于饱和状态。

在以上既定因素限制下，用混合平均车头时距代替饱和车头时距，混合平均饱和车头时距的计算式为[8]：

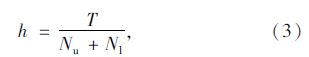
式中，h为混合平均车头时距；T为左转专用相位绿灯时间；Nu为调头车辆数；Nl为左转车辆数。

1.3 模型建立与分析

由于昆明市主城区(一环以内)的关键交叉口绝大多数均采取了禁左的管控措施，为了研究的合理性，选择昆明市环城东路与人民东路交叉口作为研究对象。该交叉口调头车辆较多，且具有左转专用相位。

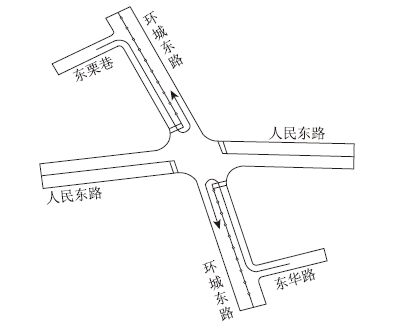
环城东路为双向六车道，在该交叉口周边的路段设置中央隔离栏，与环城东路相交的支路均采用右进右出的交通组织方式，即支路进口道左转车辆只能右转到下游信号交叉口调头，调查位置如图 2所示。

图 2 数据采集点位 Fig. 2 Data collection positions
图选项

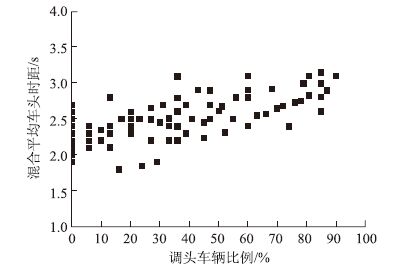
对实地调查的数据进行统计分析，把混合平均车头时距作为因变量，调头车辆比例作为自变量，混合平均车头时距-调头车辆比例散点图见图 3。

图 3 不同比率调头车对应的混合平均车头时距 Fig. 3 Different ratios of U-turn vehicles corresponding to mixed average time headways
图选项

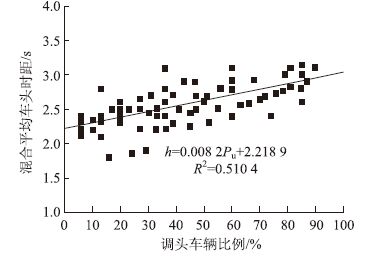
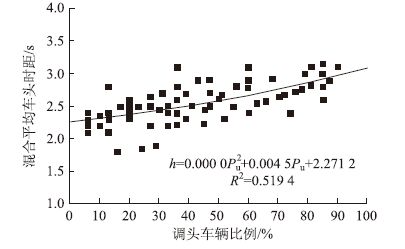
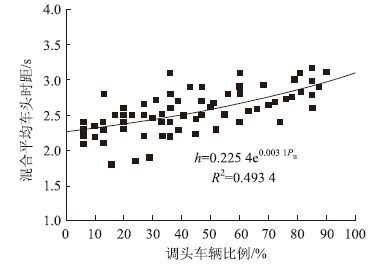
根据散点图，选取线性回归模型、二次多项式回归模型、指数回归模型等模型，通过Origin Pro 8.5对混合平均车头时距-调头车辆比例进行回归分析，结果如图 4～图 6所示(图中的R2为回归模型的相关系数)，对比分析结果如表 2所示。

图 4 线性回归模型 Fig. 4 Liner regression model
图选项

图 5 二次多项式回归模型 Fig. 5 Quadratic regression model
图选项

图 6 指数线性回归模型 Fig. 6 Exponential linear regression model
图选项

表 2 三种回归模型统计结果分析 Tab. 2 Analysis of statistical result of 3 regression models
模型线性回归系数 拟合系数 调整后拟合系数 标准误差
一次线性模型 h=0.008 2Pu+2.218 90.712 60.510 40.500 320.235 7
二次线性模型h=0.000 04 Pu2+ 0.004 5Pu + 2.271 20.706 00.519 40.512 20.253 7
指数线性回归模型 h=2.225 4e0.003 1Pu0.715 40.493 40.486 20.263 8
表选项

结果显示，二次多项式回归模型具有最好的拟合度，因此，选择该拟合曲线作为混合平均车头时距h和调头车辆比例Pu的关系模型，模型方程为：

式中

由回归模型方程可知，当调头车辆比例为零时，饱和车头时距h0为2.271 2 s。由此可得调头车辆的修正系数为：

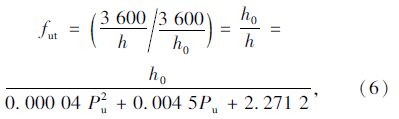
式中,fut为调头车辆修正系数；h为混合平均车头时距；h0为无调头车辆时左转车辆的平均车头时距。

通过式(6)可以求出不同调头车辆比例情况下的修正系数，其结果如表 3所示。

表 3 不同的调头车辆比例情况下的修正系数 Tab. 3 Correction coefficients of different percentages of U-turn vehicle
Pu/%102030405060708090100
fut0.980.960.930.910.880.850.820.790.760.73
表选项

由表 3可知，调头车流对左转专用车道的饱和流率确实存在影响，而且其影响也比较明显。随着调头车辆比例的增加，修正系数也呈现出逐步增加的趋势，其对左转饱和流率的影响逐步增加。由式(6)及表(3)的结果，可以计算出不同调头车辆比例情况下左转专用车道的饱和流率。由通行能力的计算公式，在其他条件不变的情况下，可以得出调头车辆对交叉口通行能力的影响结果。然而，设置中央隔离栏的最终目的是为了提高设置区域的交通运行效率[9]，因此，利用直接左转和远引调头的行程时间和延误，可以得到设置中央隔离栏后行程时间和延误的差值为：

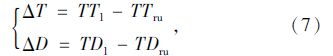
式中,TTl，TTru分别为直接左转平均行程时间和远引调头平均行程时间;TDl，TDru分别为直接左转平均延误和远引调头平均延误。

只有当ΔT和ΔD同时大于零时，设置中央隔离栏后的交通运行效率才会得到最大的提高；当ΔT=0，ΔD=0时,所对应的转移交通量和主干路交通量为主干路设置中央隔离栏后的流量阈值。

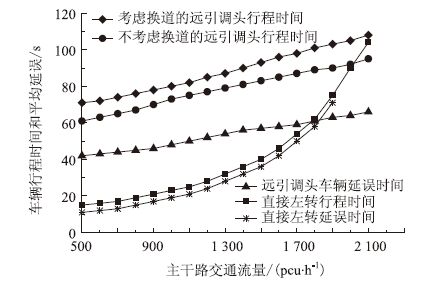
由文献[10]可知，直接左转和远引调头运行效率分析结果显示，不同主干路流量下这两种组织方式下的行程时间和延误可用支路车流的最大值(250 pcu/h)来对比分析，其结果如图 7所示。

图 7 两种组织方式下行程时间和延误模型比较 Fig. 7 Comparison of travel time and delays of 2 organization modes
图选项

从图 7可以看出，在支路转移交通量为250 pcu/h的情况下，对于行程时间而言，当主干路交通流大于1 900 pcu/h时，直接左转的行程时间大于远引调头的行程时间；对于平均延误而言，当主干路交通流量大于1 800 pcu/h时，直接左转的平均延误大于远引调头的平均延误。综上所述，当主干路交通流大于1 900 pcu/h时，远引调头的运行效率高于直接左转的运行效率。因此，主干路设置中央隔离栏的流量阈值分别为支路250 pcu/h和主干路1 900 pcu/h。由式(5)可以得出，调头流量的百分比为21%，将其代入式(6)可以得到调头车辆的修正系数为0.95，即左转专用车道的通行能力降低了5%。在主干路上设置中央隔离栏以后，当调头流量百分比小于21%时，尽管交叉口通行能力有所降低，但是远引调头的运行效率将比直接左转的高，此时设置中央隔离栏对提高主干路的交通运行效率有积极意义。

2 对无信号控制交叉口的影响

对于无信号交叉口，其交通组织一般属于自组织的范畴[11]。在未转移交通量之前，在自组织的作用下，交叉口的交通组织处于相对稳定的状态。但由于转移交通量的出现，将打破原有的交通状态，对交叉口产生一定的影响。这些影响主要体现在对交叉口通行能力的影响。基于此，本节将重点分析转移交通量对无信号交叉口通行能力的影响。

上一节已经分析了转移交通流对信号交叉口主干路通行能力的影响，对于无信号交叉口，转移交通流对主干路通行能力的影响与信号交叉口的类似，本节将不再赘述。本节运用可接受间隙理论来探讨转移交通流对无信号交叉口次要道路(支路)通行能力的影响[12]。

可接受间隙模型已经被广泛运用于计算无信号交叉口支路的通行能力。而大多数可接受间隙模型均可追溯到Siegloch的通行能力公式。根据Siegloch的通行能力公式，支路通行能力为[13]：

式中，C为支路通行能力；qp为主路交通流量；f(t)为主路车头时距概率分布函数；g(t)为主路车头时距t内支路可通过主路上的车辆数。以Siegloch的通行能力公式为基础，不同的f(t)和g(t)对应着不同的通行能力模型。f(t)的主要形式在上节已经分析过，此处不再赘述。g(t)是一个逐步常数函数，表示车头时距t内可以通过主路的车辆数，计算式为[14]：
式中，pn(t)为车头时距t内支路可通过主路上n辆车的概率，其表达式为：
式中，tc为支路车流穿越主路车流的临界间隙；tf为支路车流穿越主路车流的随车时距。

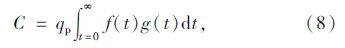
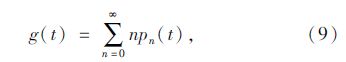
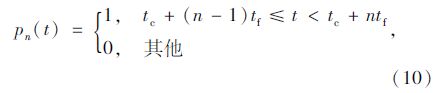
根据上述分析，得到不同f(t)和g(t)情况下的通行能力为：

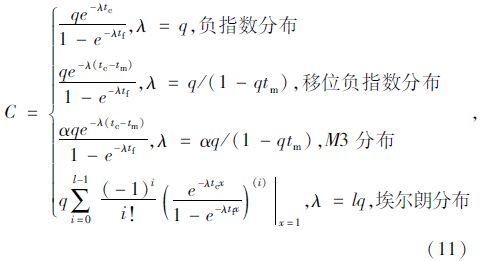
式中，q为主干路交通流量；tm为位移量；λ为车流的平均到达率;α为按自由流状态行驶的车辆所占的比例;l为分布参数可以认为是非随机性程度的一种粗略表示，车流的非随机性程度随着其增加而增加;i为到达车辆数;x为支路饱和度。

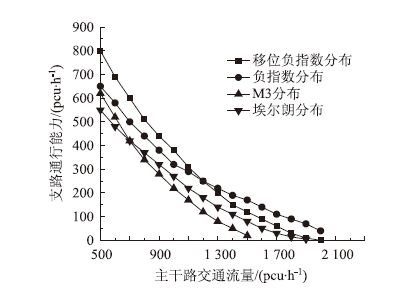
综上所述，不同的主干路车头时距分布对应着不同的支路的通行能力计算公式。上述几种不同的通行能力曲线如图 8所示。其中，取tc=6 s，tf=3 s；对于移位负指数分布，位移量tm取1.2 s，对于M3分布tm取2.4 s，埃尔朗分布的阶数取二阶。

图 8 主干路不同车头时距情况下对应的支路通行能力 Fig. 8 Capacities of branch road corresponding to different time headways on arterial road
图选项

由图 8可以看出，当主干路车流的车头时距服从负指数分布和移位负指数分布时，它们所对应的支路的通行能力很接近，特别是当主干路流量为1 200 pcu/h 时，两种分布函数的支路通行能力趋于相等。同时，在主干路流量小于850 pcu/h时，不同的主干路车头时距对应的支路通行能力比较接近，即不同的主干路车头时距对支路的通行能影响较小。当主干路流量大于1 250 pcu/h时，不同的主干路车头时距对应的支路通行能力差异较大，即不同的主干路车头时距对支路的通行能影响较大。

3 结论

本文主要分析了转移交通流对下游交叉口通行能力的影响。首先分析了信号交叉口饱和流率的计算方法，选取了实地调查平均饱和车头时距的方法计算饱和流率。其次引入调头调整系数，对所得的调查数据进行了回归分析，得出如下结论：

(1)转移交通流对下游信号交叉口通行能力的影响：在主干路上设置中央隔离栏后，当调头流量百分比小于21%时，尽管交叉口通行能力有所降低，但远引调头的运行效率将比直接左转的高，此时设置中央隔离栏对提高主干路交通运行效率有积极意义。

(2)转移交通流对无下游信号交叉口通行能力的影响：在主干路流量小于850 pcu/h时，不同的主干路车头时距对应的支路通行能力比较接近，即不同的主干路车头时距对支路的通行能影响较小。当主干路流量大于1 250 pcu/h时，不同的主干路车头时距对应的支路通行能力差异较大，即不同的主干路车头时距对支路的通行能力影响较大。

参考文献
[1] 刘峰.中央隔离条件下路段左转交通流转移机理研究[D].昆明:昆明理工大学,2012. LIU Feng. Research on Transfer Mechanism of Left Turn Traffic Flow under the Condition of Central Isolation Fence[D].Kunming: Kunming University of Science and Technology,2012.
[2] PAN Liu. Evaluation of the Operational Effects of U-turn Movement[D]. Tampa, FL: University of South Florida,2006.
[3] YANG Xiao-kuan, ZHOU Hua-gu. CORSIM-based Simulation Approach to Evaluation of Direct Left Turn versus Right Turn Plus U-turn from Driveways[J].
[4] Transportation Research Board. Highway Capacity Manual 2000[M/CD]. Washington, D. C.: National Research Council, 2000.
[5] TSAO S M, CHU S W. A Study on Adjustment Factors for U-turns in Left-turn Lanes at Signalized Intersections [J].
[6] 朱传万.远引调头对下游信号交叉口交通流的影响分析[D].长春:吉林大学,2008. ZHU Chuan-wan. Research on Influence of U-turn upon Traffic Flow at Downstream Signalized Intersection[D].Changchun: Jilin University,2008.
[7] 刘明君.基于混合交通流的信号交叉口机动车车头时距研究[D].北京:北京交通大学,2010. LIU Ming-jun. Research on Discharge Headway with Heterogeneous Traffic at Signalized Intersections[D].Beijing: Beijing Jiaotong University,2010.
[8] 郑倩.远引调头组织方式的交通效果评价研究[D].长春:吉林大学,2007. ZHENG Qian. Research on Operational Effects of Right Turns Followed by U-turns [D].Changchun:Jilin University,2007.
[9] 蒋卫东,周磊,乐逸祥.道路中央分离带的安全性分析[J].公路与汽运,2003(5):49-51. JIANG Wei-dong, ZHOU Lei, YUE Yi-xiang. Safety Analysis of Central Isolation Fence[J]. Highways and Automotive Applications, 2003(5):49-51.
[10] 刘荣贵,中央隔离条件下支路交通流转移机理研究[D].昆明:昆明理工大学,2014. LIU Rong-gui. Research on Transfer Mechanism of Branch Traffic Flow under the Condition of Central Isolation Fence[D].Kunming: Kunming University of Science and Technology,2014.
[11] 翟忠民,道路交通组织优化[M].北京:人民交通出版社,2004. ZHAI Zhong-min. Road Traffic Organizational Optimization[M]. Beijing: China Communications Press, 2004.
[12] 郑柯,张起森.无信号交叉口可接受间隙理论模型修正分析[J].长沙交通学院学报,2001,17(1): 36-38. ZHENG Ke, ZHANG Qi-sen. Analysis of Amending Gap Acceptance Theory's Model at Unsignalized Intersections [J]. Journal of Changsha Communications University, 2001,17(1): 36-38.
[13] FAN Jing-jing. Operational Evaluation of Right Turns Followed by U-turns at Signalized Intersections as an Alternative to Direct Left Turns[D]. Tampa, FL: University of South Florida,2006.
[14] KYTE M, TIAN Z, MIR Z, et al. Capacity and Level of Service at Unsignalized Intersections, NCHRP Report 346[R]. Washington, D.C.: National Cooperative Highway Research Program, TRB, 1996.