扩展功能
文章信息
- 齐宏学, 高小妮, 贺拴海
- QI Hong-xue, GAO Xiao-ni, HE Shuan-hai
- 斜拉-自锚式悬索组合体系桥梁结构参数变化对活荷载效应影响
- Influence of Change of Structure Parameters of Cable-stayed and Self-anchored Suspension Combination Bridge on Live Load Effect
- 公路交通科技, 2015, Vol. 31 (11): 81-87,93
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (11): 81-87,93
- 10.3969/j.issn.1002-0268.2015.11.013
-
文章历史
- 收稿日期: 2014-11-21
2. 交通运输部公路科学研究院, 北京 100088;
3. 长安大学 桥梁与隧道陕西省重点实验室, 陕西 西安 710064
2. Research Institute of Highway, Ministry of Transport, Beijing 100088, China;
3. Key Laboratory for Bridge and Tunnel of Shaanxi Province, Chang'an University, Xi'an Shaanxi 710064, China
斜拉-悬索协作体系桥是将悬索桥[1, 2, 3, 4, 5]和斜拉桥结合[6]后形成的一种缆索承重体系桥梁,其悬索部分较同跨径的悬索桥有所减小,进而减小主缆力,降低锚碇的造价,在结构施工和成桥状态具有较好的抗风稳定性。国内建成的有贵州乌江大桥和大连庄河建设大桥。国内外学者对该体系桥梁进行了大量研究,对活载作用下的非线性效应也进行了一些研究,如王会利应用线性理论、线性二阶理论和非线性理论对一座主跨800 m的自锚式斜拉-悬索协作体系桥进行了分析;宋爱清[7]结合一座自锚式斜拉悬索协作体系桥的方案设计,采用了非线性和线性二阶两种方法对活载作用下的结构体系进行了对比计算;周云岗[8]根据斜拉-悬吊协作桥的受力特点,建立了结构简化计算模型,并采用实例对计算模型进行了验证。
然而,多塔斜拉-自锚式悬索组合体系桥梁不同于常规斜拉-悬索协作体系桥,组合体系桥梁具有跨越能力强、结构美观和两种缆索体系桥相互影响的特点,其主缆力、加劲梁变位、斜拉索力和背索力相互影响,受力复杂,且非线性效应较明显。国内对该体系桥梁研究较少,长安大学徐岳[9]教授对独塔组合体系桥梁静力性能进行了有限元分析和实桥缩尺模型试验研究;长安大学赵煜[10, 11]教授对多塔组合体系桥梁进行了模型试验和计算方法研究。对于缆索体系桥梁[12]的研究重点之一就是其非线性效应,以及在活载作用下组合体系桥的受力特点。本文以某三塔斜拉-自锚式悬索组合体系桥梁为工程背景,针对活载下该桥的非线性效应展开研究,进而讨论其在活载作用下的参数影响特征。
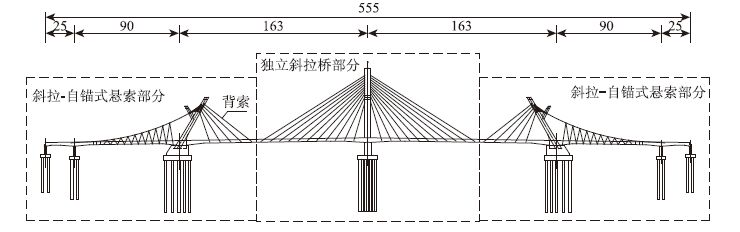
1 主要构造某三塔斜拉-自锚式悬索组合体系桥梁[13]跨径组成为:25+90+2×162.5+90+25=555 m,由独立斜拉桥部分与斜拉-自锚式悬索部分组成。斜拉桥部分的塔称为主塔,桥面以上塔高60 m,悬索桥部分的塔称为副塔,桥面以上塔高35 m。加劲梁宽40 m。全桥总体布置如图 1所示。
|
| 图 1 斜拉-自锚式悬索组合体系桥立面布置图(单位:m) Fig. 1 Layout of cable-stayed and self-anchored suspension combination bridge (unit:m) |
利用桥梁专用有限元软件midas对结构进行计算,结构中主缆采用索单元,背索和斜拉索采用桁架单元,主梁及桥塔模拟采用梁单元。副塔墩处支座通过只受压约束,塔梁连接处采用主从约束实现墩塔梁固结,斜拉索及吊杆与主梁通过钢臂连接。全桥计算模型采用脊骨梁模型。全桥有限元模型及单元离散如图 2所示。

|
| 图 2 全桥有限元模型 Fig. 2 Finite element model of bridge |
对于结构平衡状态的建立,首先采用悬索理论和最小弯曲能量法并结合柔性迭代法确定自锚式悬索部分的初步几何和受力状态,然后采用最小弯曲能量法和影响矩阵法并结合迭代算法初步确定独立斜拉桥部分的几何和受力状态。再将两部分独立模型组合在整体模型中,并对整体模型进行非线性的迭代计算求得合理成桥状态。
3 活荷载作用下非线性分析缆索体系桥梁存在着明显的几何非线性[14],在活荷载作用下使用叠加原理将失效,不能用线性影响线加载方法计算结构内力及位移包络图。若想准确计算活载作用下体系的内力和位移等效应,就必须采用非线性的分析方法,但其迭代分析计算量大。因此,引入简化的近似计算方法——线性二阶加载方法[15]。
(1)活荷载线性二阶理论和非线性理论
线性二阶加载分析是指仅计入恒载的非线性影响,用单位荷载沿桥纵向移动,就可得到各量值的影响线,得到车辆最不利的加载位置,应用叠加原理,即可求得车辆荷载产生的位移、内力包络图。
对于非线性加载,即可利用线性二阶加载所确定的最不利加车位置,利用非线性分析求得位移、内力包络图等。
在活载作用下利用桥梁软件midas分别采用线性二阶与非线性理论对结构进行分析。活荷载模拟采用均布荷载进行加载,单车道活载集度采用10 kN/m。
(2)组合体系桥梁活载分析计算方法比较
① 位移
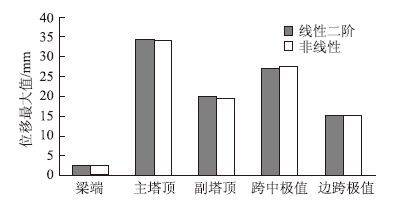
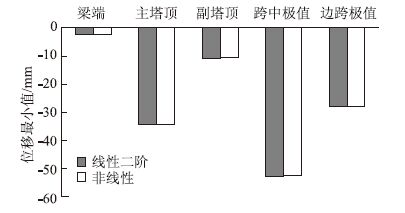
通过梁端、主塔顶和副塔顶水平位移极值以及主梁跨中和边梁跨中竖向位移极值,来分析采用线性二阶与非线性理论所计算的活荷载效应情况。两种理论计算的控制截面活荷载最大和最小位移如图 3、图 4所示。由图中两种理论计算的结果对比看出:除主梁跨中和边跨位移极值外,线性二阶计算所得的活载位移最大值较非线性计算所得结果大;所选控制位置由线性二阶方法计算所得的活载位移最小值较非线性计算结果大。
|
| 图 3 控制截面位移最大值 Fig. 3 Maximum displacement of critical section |
|
| 图 4 控制截面位移最小值 Fig. 4 Minimum displacement of critical section |
从数值来看,两种理论计算所得的梁端水平位移的误差较其他控制截面误差大。梁端水平位移线性二阶计算最大值为2.41 mm,非线性计算最大值为2.36 mm,二者误差为2.1%。梁端水平位移线性二阶计算最小值为-2.31 mm,非线性计算最小值为-2.2 mm,二者误差为4%。两种理论计算的控制截面位移误差最大为4%,因此从工程角度上而言,线性二阶理论计算的位移值与非线性理论计算结果较接近。
②内力
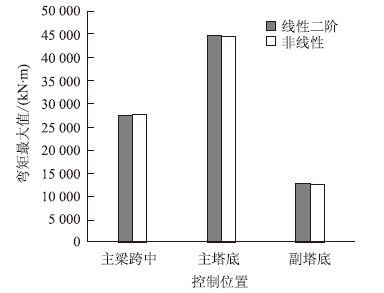
以主梁跨中、主塔、副塔及缆索内力极值为研究对象,来分析采用线性二阶与非线性理论所计算的活荷载效应情况。线性二阶与非线性计算的控制截面活荷载最大和最小内力对比情况如图 5~图 9所示。
|
| 图 5 控制位置弯矩最大值 Fig. 5 Maximum bending moment of critical position |

|
| 图 6 控制位置弯矩最小值 Fig. 6 Minimum bending moment of critical position |
|
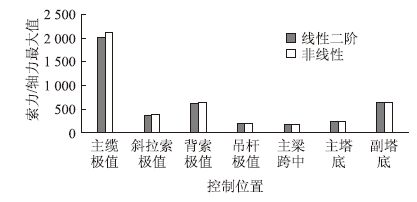
| 图 7 控制位置索力/轴力最大值(单位:kN) Fig. 7 Maximum cable tension or axial force of critical position(unit:kN) |

|
| 图 8 控制位置索力最小值 Fig. 8 Minimum cable tension of critical position |

|
| 图 9 控制位置轴力最小值 Fig. 9 Minimum axial force of critical position |
对比图中两种理论的计算结果可看出:除主梁跨中弯矩外,线性二阶计算所得的活载弯矩最大值和最小值较非线性计算所得结果大;所选控制位置,除斜拉索索力外,其余缆索力采用线性二阶计算所得的活载索力最大值较非线性计算所得结果小;所选控制位置,除背索索力外,其余缆索力采用线性二阶计算所得的活载索力最小值较非线性计算所得结果小;所选控制位置,除主跨跨中轴力外,其余截面轴力采用线性二阶计算所得的活载轴力最大值较非线性计算所得结果小;所选控制位置,除主塔塔底轴力外,其余截面轴力采用线性二阶计算所得的活载轴力最小值较非线性计算所得结果小。
从数值来看两种理论计算的控制截面弯矩中,主梁跨中最小弯矩值的误差较其他控制截面弯矩值误差大,主梁跨中弯矩线性二阶计算最小值为-10 702 kN·m,非线性计算最小值为-11 083 kN·m,二者误差为3.6%;两种理论计算的控制截面索力中,主缆缆力最大值误差较其他控制截面索力值误差大,主缆缆力线性二阶计算最大值为2 019 kN,非线性计算最大值为2 119 kN,二者误差为4.9%;两种理论计算的控制截面轴力中,主梁跨中轴力最小值误差较其他控制截面误差大,主梁跨中轴力线性二阶计算最小值为4 816 kN,非线性计算最大值为4 917 kN,二者误差为2.2%。可以看出,两种理论计算的控制截面内力误差最大为4.9%。
由以上位移和内力的比较分析可见,两种理论计算结果较接近,误差在5%之内。对于该类结构,在满足工程要求的情况下,可以采用线性二阶理论计算活载效应。
4 参数变化对结构受力性能影响分析多塔斜拉-自锚式悬索组合体系桥梁可供参考资料较少,数值模拟分析方法是构件参数选取的方法之一。本文以三塔斜拉-自锚式悬索桥为例,针对斜拉-自锚式悬索组合体系桥梁构件参数进行研究。结合线性二阶理论,通过构件参数如主缆刚度、主梁刚度及塔的刚度等对主梁跨中挠度、主梁合龙处(独立斜拉桥与自锚式斜拉-悬索组合体系结合处)弯矩、主缆轴力等力学指标的影响情况对比分析,确定构件参数变化对结构影响情况,为该类桥梁的设计提供参考。
主缆、主梁及塔刚度等的变化主要通过构件的弹性模量和截面面积进行变化来实现,构件弹性模量如表 1所示。在确保主梁线性不变的情况下,对结构进行迭代分析确定新的平衡状态。
| 构件 | 主缆 | 吊杆 | 背索 | 斜拉索 | 副塔 | 主梁 | 主塔 | |
| 混凝土 | 钢混 | |||||||
| 弹性模量/(kN·m-2) | 2.05e8 | 2.05e8 | 2.05e8 | 1.95e8 | 2.06e8 | 3.45e7 | 2.06e8 | 3.45e7 |
| 截面面积/m2 | 0.11 | 0.003 5 | 0.011 5 | 0.012 7 | 2.5 | 31.02 | 3.02 | 12 |
(1) 主梁轴向刚度的影响
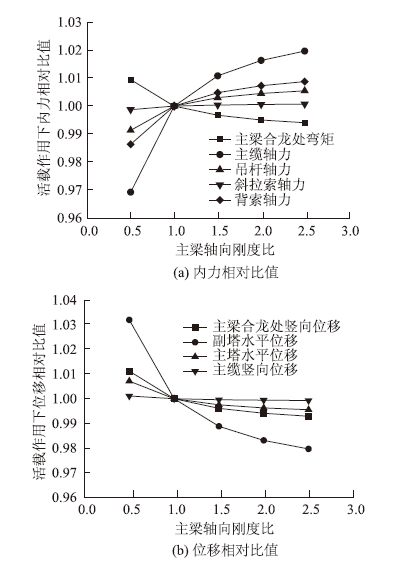
图 10为主梁轴向刚度比分别取0.5,1.0,1.5,2.0和2.5时,结构的内力及位移的相对比值。可以看出:①随着主梁轴向刚度的增加,合龙处主梁位移和弯矩、副塔位移、主塔位移及主缆竖向位移均减小;主缆缆力、吊杆轴力、背索索力及斜拉索索力有所增加。②主梁轴向刚度比在0.5~2.5变化时,控制截面弯矩、轴力及索力比值在0.968~1.02之间,主缆缆力相对比值变化范围最大;控制截面位移比值在0.98~1.033之间,副塔水平位移相对比值变化范围最大。可见,主梁轴向刚度比在0.5~2.5变化时,对副塔的位移和主缆缆力影响相对较大,但对结构整体受力的影响较小。
|
| 图 10 主梁轴向刚度变化对结构力学性能影响 Fig. 10 Influence of axial stiffness change of main girder on mechanical performance of structure |
(2) 主梁抗弯刚度的影响
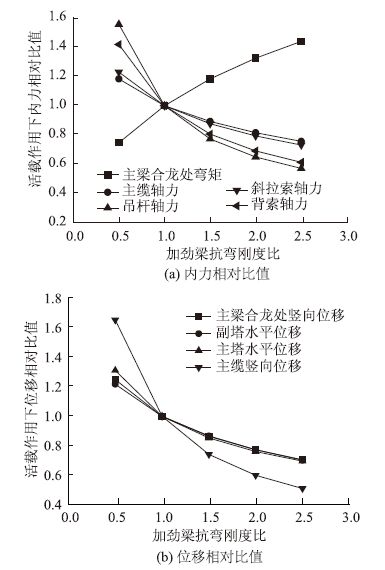
图 11为主梁抗弯刚度比分别取0.5,1.0,1.5,2.0和2.5时,结构的内力及位移的相对比值。可以看出:①随着主梁抗弯刚度的增加,除主梁合龙处弯矩外,其余控制截面内力和位移均减小。②主梁刚度在0.5~2.5变化时,控制截面弯矩、轴力及索力比值在0.57~1.57之间,吊杆轴力相对比值变化范围最大;控制截面位移比值在0.51~1.67之间,主缆竖向变位相对比值变化范围最大。可见,主梁抗弯刚度在0.5~2.5变化时,对主缆竖向位移及吊杆轴力影响较显著。随着主梁抗弯刚度的增加,缆索所分担的活载比例在减小,而主梁承担的活载比例在增加,符合荷载按刚度分配的原则。
|
| 图 11 主梁抗弯刚度变化对结构力学性能影响 Fig. 11 nfluence of flexural rigidity change of main girder on mechanical performance of structure |
(3) 主塔刚度的影响
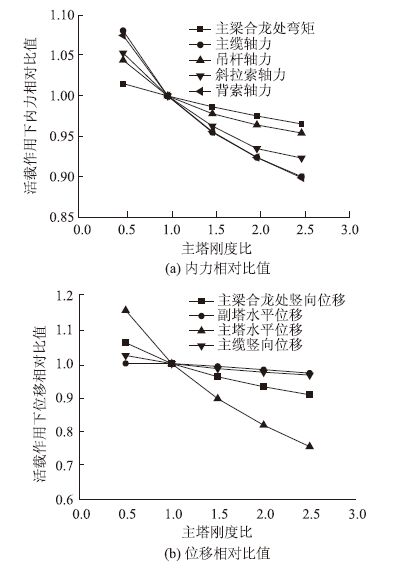
通过改变主塔截面面积来改变主塔刚度。图 12为主塔刚度比分别取0.5,1.0,1.5,2.0和2.5时,结构的内力及位移的相对比值。可以看出:①随着主塔刚度的增加,控制截面内力、缆索力及控制位置位移均逐渐减小。②主塔刚度在0.5~2.5变化时,控制截面弯矩、轴力及索力比值在0.9~1.08之间,主缆力与背索索力相对比值变化范围最大;控制截面位移比值在0.75~1.16之间,主塔水平位移相对比值变化范围最大。可见,主塔刚度在0.5~2.5变化时,对结构的影响不显著。随着主塔刚度的增大,斜拉部分及斜拉-自锚式协作部分刚度均增加,说明在活荷载作用下,斜拉部分与斜拉-自锚式协作部分共同受力,结构协作性较强。
|
| 图 12 主塔刚度变化对结构力学性能影响 Fig. 12 Influence of stiffness change of main pylon on mechanical performance of structure |
(4)主缆刚度的影响
在组合体系中斜拉-自锚式组合部分,主缆一端锚固于主梁,另一端锚固于副塔,主缆荷载通过副塔传递至基础,主缆是该部分结构中重要组成部位。对三塔斜拉-自锚式悬索组合体系桥主缆刚度比取为原方案刚度的0.5,1.5,2.0,2.5倍,研究其对结构的受力特性影响。通过改变主缆弹性模量来改变主缆刚度,采用不同主缆刚度进行计算分析,结构的内力及位移的相对比值结果见图 13。

|
| 图 13 主缆刚度变化对结构力学性能影响 Fig. 13 Influence of stiffness change of main cable on mechanical performance of structure |
由图 13可见,随着主缆刚度的增大,主缆缆力、背索索力及吊杆力在逐渐增大,而斜拉索索力和主梁合龙处弯矩值在逐渐减小。当主缆刚度在0.5~2.5变化时,控制截面弯矩、轴力及索力比值在0.71~1.36之间,主缆缆力相对比值变化范围最大;主缆刚度比在0.5~2.5变化时,构件主要位置的位移均在逐渐减小,除副塔水平向位移外,其余构件的位移比在0.88~1.11之间。当主缆刚度比为0.5时,副塔水平向位移比为1.24;当主缆刚度比为2.5时,副塔水平向位移比为0.71。
可见,主缆刚度比在0.5~2.5变化时,结构的内力及位移比在0.71~1.36之间,主缆刚度变化对结构刚度的影响较大。根据荷载按刚度分配原则,主缆刚度的增加对主缆轴力影响较显著,因而对副塔水平向变位的影响亦较大,同时使斜拉-自锚式协作部分在全桥受力体系中贡献比例变大。
(5) 副塔刚度的影响
通过改变副塔截面面积来改变副塔刚度,采用不同副塔刚度计算分析,控制截面的内力和位移比见图 14。

|
| 图 14 副塔刚度变化对结构力学性能影响 Fig. 14 Influence of stiffness change of side pylon on mechanical performance of structure |
由图 14可见,随着副塔刚度的增大,除背索索力逐渐增大外,其余控制截面弯矩、缆力和轴力均逐渐减小。副塔刚度在0.5~2.5变化时,控制截面弯矩、轴力及索力比值在0.82~1.12之间,主缆力与背索索力相对比值变化范围最大。随着副塔刚度的增大,控制位置的位移均逐渐减小,副塔刚度在0.5~2.5变化时,副塔水平向位移比在0.69~1.17间变化,副塔刚度的变化对副塔水平向位移影响较大。
可见,副塔刚度的变化,使得结构整体刚度提高。副塔刚度比在0.5~2.5变化时,结构的内力及位移比在0.69~1.17之间,副塔刚度的变化对副塔自身及锚固于其上的主缆及背索影响较大。
5 结论以某斜拉-自锚式悬索组合体系桥梁为研究背景,对其进行活载作用下的非线性分析,并选取不同的结构参数,如主梁刚度、桥塔刚度及主缆刚度等,来分析在活载作用下结构的受力情况,得到如下结论:
(1)主跨跨径达到160 m的三塔斜拉-自锚式组合体系桥梁在活荷载作用下,其线性二阶理论与非线性理论计算结果较接近,误差在5%之内。在满足工程精度的要求下,为简化计算可采用线性二阶理论进行结构分析。
(2)斜拉-自锚式悬索组合体系桥中任一部件的变化对结构都有影响,主梁抗弯刚度、主缆刚度的变化对结构受力性能影响较大,主梁轴向刚度、副塔轴向刚度及主塔轴向刚度的变化对结构受力性能影响较小。
(3)在斜拉-自锚式悬索组合体系桥梁设计中,结构主梁和主缆参数变化对结构受力影响较大,在设计中选取参数时应给予足够重视。
| [1] | 潘永仁.悬索桥结构非线性分析理论与方法[M].北京:人民交通出版社,2005. PAN Yong-ren. Non-linear Analysis Theory and Method for Suspension Bridge Structures[M]. Beijing: China Communications Press, 2005. |
| [2] | ÇEVIK M, PAKDEMIRLI M. Non-linear Vibrations of Suspension Bridges with External Excitation[J]. |
| [3] | BOONYAPINYO V,LAUHATANON Y,LUKKUNA- PRASIT P.Nonlinear Aerostatic Stability Analysis of Suspension Bridges[J]. |
| [4] | MATSON D D. Lions' Gate Suspension Bridge: Design of the Suspended Structure Replacement[C]//Metropolis and Beyond: Proceedings of the 2005 Structures Congress and the 2005 Forensic Engineering Symposium. New York: ASCE, 2005. |
| [5] | 张哲. 混凝土自锚式悬索桥[M]. 北京: 人民交通出版社, 2005. ZHANG Zhe. Concrete Self-anchored Suspension Bridge[M]. Beijing: China Communications Press, 2005. |
| [6] | BRUNO D, LEONARDI A. Natural Periods of Long-span Cable-stayed Bridges[J]. |
| [7] | 宋爱清,李箴,吴宏业.自锚式斜拉-悬索协作体系桥活载响应分析[J].北方交通,2011(4):65-67. SONG Ai-qing, LI Zhen, WU Hong-ye. Live Load Response Analysis on Self-anchored Cable-stayed-suspension Cooperative System Bridge[J]. Northern Communications, 2011(4):65-67. |
| [8] | 周云岗,肖汝诚.多塔斜拉-悬吊协作桥活载效应近似计算方法[J].同济大学学报:自然科学版,2013,41(11):1609-1617. ZHOU Yun-gang, XIAO Ru-cheng. Approximate Analysis Method of Multi-tower Cable-stayed Suspension Bridges Under Live Load[J]. Journal of Tongji University:Natural Science Edition, 2013,41(11):1609-1617. |
| [9] | 徐岳,邹存俊,任更锋,等.自锚式悬索与斜拉组合体系桥梁使用阶段模型试验[J].长安大学学报:自然科学版,2009,29(2):46-50. XU Yue, ZOU Cun-jun,REN Geng-feng,et al. Model Test of Self-anchored Suspension and Cable-stayed Combination Bridge in Service Stage [J]. Journal of Chang'an University:Natural Science Edition, 2009,29(2):46-50. |
| [10] | 赵煜,张锋,周勇军,等,多跨斜拉-自锚式悬索组合体系桥全桥静力模型试验[J].长安大学学报:自然科学版,2012,32(5):45-51. ZHAO Yu, ZHANG Feng, ZHOU Yong-jun,et al. Static Model Test of Multi-Span Cable-Stayed and Self-anchored Suspension Composite Bridge[J]. Journal of Chang'an University:Natural Science Edition, 2012, 32(5):45-51. |
| [11] | 高小妮, 贺拴海, 赵煜,等. 三塔斜拉-自锚式悬索组合体系桥成桥阶段活载模型试验研究, 武汉理工大学学报, 2012, 34(1): 84-89. GAO Xiao-ni, HE Shuan-hai, ZHAO Yu, et al. Model Test on Cable-stayed and Self-anchored Suspension Combination Bridge with Three Towers Under Live Loading in Finished Stage [J]. Journal of Wuhan University of Technology, 2012, 34(1): 84-89. |
| [12] | 赵煜,汤金涛,周勇军,等.三塔斜拉-自锚式悬索组合结构计算方法及参数分析[J].西安科技大学学报,2011,31(5):573-579. ZHAO Yu, TANG Jin-tao, ZHOU Yong-jun, et al. Calculation Method and Parameter Analysis of Self-anchored Suspension and Cable-Stayed Composite Structure with Three Towers[J].Journal of Xi'an University of Science and Technology, 2011, 31(5):573-579. |
| [13] | 高小妮. 多塔斜拉-自锚式悬索组合体系桥梁结构理论分析与模型试验研究[D]. 西安:长安大学, 2012. GAO Xiao-ni. Theoretical Analysis and Model Test Study on Cable-stayed and Self-anchored Suspension Combination Bridge with Multi-tower[D]. Xi'an: Chang'an University, 2012. |
| [14] | KAROUMI R. Some Modeling Aspects in the Nonlinear Finite Element Analysis of Cable Supported Bridges[J]. |
| [15] | 梁鹏, 秦建国, 袁卫军. 超大跨度斜拉桥活载几何非线性分析 [J].公路交通科技,2006,23(4):60-62. LIANG Peng, QIN Jian-guo, YUAN Wei-jun. Geometrical Nonlinear Analysis under Live Load for Super Long Span Cable-stayed Bridges[J]. Journal of Highway and Transportation Research and Development, 2006, 23(4):60-62. |
 2015, Vol. 31
2015, Vol. 31
