扩展功能
文章信息
- 何琳, 王家林
- HE Lin, WANG Jia-lin
- 模拟有效预应力的等效荷载-实体力筋降温法
- Method of Equivalent Load and Temperature Reduction on Prestressing Tendon for Effective Prestress Simulation
- 公路交通科技, 2015, Vol. 31 (11): 75-80
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (11): 75-80
- 10.3969/j.issn.1002-0268.2015.11.012
-
文章历史
- 收稿日期: 2014-08-18
预应力混凝土结构在土木工程特别是桥梁工程中得到广泛使用,使用预应力技术可增加混凝土结构的弹性工作范围,提高结构的强度和承载力,延长结构使用寿命。
通过有限元数值方法准确地揭示和模拟预应力混凝土结构的真实力学状态,对预应力混凝土结构的设计、施工及使用的安全性具有重要意义。对于预应力的模拟,目前普遍采用的方法有等效荷载法和实体力筋法两种。
对于预应力筋的有效预应力,等效荷载法[1, 2, 3]将预应力筋从结构中取出,用一组等效荷载代替预应力筋对混凝土的作用,其优点是建模简单,可以准确模拟考虑各种损失后的有效预应力,其主要缺点是不能考虑预应力筋的刚度贡献和承载作用[4, 5]。黄侨等[6]在关于预应力的等效荷载数值计算时,提出了基于NURBS预应力束的几何模型,弥补常用折线逼近法的不足,更准确地计算预应力束等效荷载,进行预应力混凝土预应力效应的分析。
实体力筋法是在建模中分别用不同的单元模拟混凝土和预应力筋,通过建立预应力筋节点与混凝土单元的位移约束关系实现两者的连接和共同工作,采用降温法或初应变法模拟预应力的施加[7, 8, 9, 10, 11, 12, 13, 14, 15]。通过等效降温法或等效应变法这种间接预应力加载方式进行结构分析后发现,如果直接施加预设张拉力,结构变形后筋的最后张拉力发生变化,达不到初张拉力的数值。陈玉峰[7]提出采用初应变扩大系数或单元生死法,可以准确加载目标预应力效果,但该扩大系数法需不断调整初应变,修正扩大系数,最后得到理想的结果,需要考虑索自重时,杀死该单元,将其自重采用等效节点力同时考虑。周江[13]提出通过施加等效温度荷载直接计算预应力混凝土结构次内力的方法,以得出更接近实际的计算结果。
本文基于预应力筋与混凝土共同工作、共同承载的理念,通过等效荷载法获得无筋模型的混凝土弹性收缩,根据该弹性收缩量得到预应力筋的等效降温值,从而在有筋模型中实现有效预应力的准确模拟。该方法能便捷地在多种有限元通用软件中得以实现,为模拟预应力混凝土结构张拉加载提供了又一种有效分析方法。
1 基本原理阐述 1.1 等效荷载法原理等效荷载法应用自平衡原理,将混凝土结构中的预应力筋与结构分离,用一组等效荷载代替预应力筋对混凝土的作用,并把这种等效荷载如同外荷载一样反向施加到由混凝土和非预应力筋组成的结构上,用以计算预应力对结构产生的效应。
1.2 降温法基本原理
传统降温法的原理是将混凝土和预应力筋的作用一起考虑,通过对预应力筋单元实施温降实现预应力的施加,即为力筋单元设定一个初始温度,并且给定一个温降值,使得力筋单元产生一个收缩变形,此初始应变将使力筋产生预拉力作用,力的大小为所要达到的预应力数值。力筋的温降值按式(1)计算:
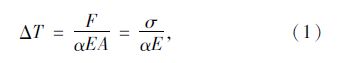
对于先张预应力筋,可以计入混凝土弹性收缩引起的预应力损失;对于后张预应力筋,式(1)根据有效预应力换算的温度降低没有考虑混凝土的弹性收缩,会导致计算后筋的应力达不到预设的应力值。
2 考虑弹性收缩的计算原理 2.1 考虑弹性收缩的等效降温计算原理设通过降温值ΔT′对预应力筋施加预应力σ,在预应力的作用下,混凝土会产生弹性收缩,混凝土的弹性收缩应变即为预应力筋的总应变,该应变用ε表示,则有:
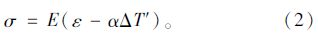
由此可得到考虑混凝土弹性收缩的等效降温计算公式:
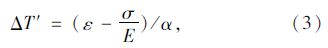
第一步:建立无预应力筋结构模型,采用等效荷载法,用一组等效荷载代替预应力筋(荷载σ)的作用施加于结构上,此时的计算结果可以正确地反映结构在预设预应力作用下的初始状态,通过力筋两点间的线位移结果,计算得到两点间的相对线位移(收缩),以及产生的弹性应变ε。
第二步:建立有筋结构模型,利用式(3),由混凝土弹性应变ε、预设预应力σ、材料参数E和α计算出考虑结构弹性收缩的力筋降温值,施加在力筋单元上,实现对有筋模型中有效预应力的准确模拟。
3 算例验证下面通过设计的线性杆件单元结构、平面单元结构、空间体单元结构验证此法的模拟效果。
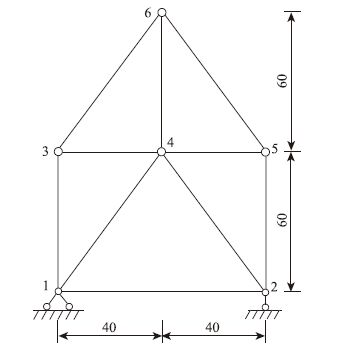
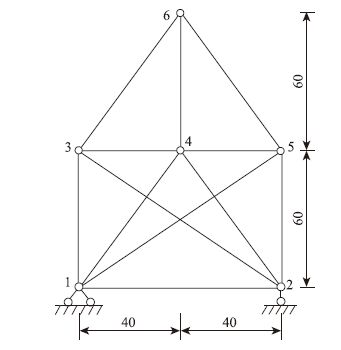
3.1 超静定桁架对于如图 1所示的平面桁架结构,各杆截面积为A=0.002 m2,弹性模量E=200 GPa,材料的热膨胀系数为α=1.0e-5 ℃-1。现欲在节点1和5之间、节点2和3之间分别张拉一根截面积和材料与其他杆相同的预应力筋(见图 2),张拉应力值为100 MPa。
|
| 图 1 桁架结构示意图(单位:cm) Fig. 1 Truss structure(unit:cm) |
|
| 图 2 含筋桁架结构示意图(单位:cm) Fig. 2 Truss structure with tendons(unit:cm) |
采用二节点桁架单元,现用不同方法模拟结构加上预应力筋张拉后的力学状态。
(1)采用等效荷载法。计算模型为图 1,在节点1和5之间、节点2和3之间施加与预应力荷载等效的相对张拉力:F=Aσ=0.002×100e6=200 kN。
(2)采用实体力筋法,计算模型为图 2,采用式(1),由张拉应力100 MPa可换算得预应力筋相应的降温值ΔT=50 ℃,即在单元15杆和23杆施加降温荷载50 ℃。
(3)根据本文方法,采用模型2,由等效荷载法的位移结果可计算得到力筋15、23节点间总应变值为-3.487 4e-4;利用式(3) 计算得考虑弹性收缩的相应降温值ΔT′=84.874 ℃;在模型2的15杆和23杆单元施加降温荷载84.874 ℃。
采用SAP2000软件,三种模拟方法计算结果见表 1、表 2。
| 节点号 | 节点1位移 | 节点5位移 | 节点2位移 | 节点3位移 |
| 等效荷载法 | (0,0) | (-0.320 0,-0.154 5) | (-0.297 4,0) | (0.022 65,-0.154 5) |
| 实体力筋法 | (0,0) | (-0.0188 5,-0.0910 3) | (-0.175 4,0) | (0.013 34,-0.091 03 |
| 本文方法 | (0,0) | (-0.320 0,-0.154 5) | (-0.297 3,0) | (0.022 65,-0.154 5) |
| 杆件号 | 13杆 | 12杆 | 45杆 | 36杆 | 23杆 |
| 等效荷载法 | -103.014 | -148.676 | -171.324 | 20.415 | — |
| 实体力筋法 | -60.688 | -87.589 | -100.932 | 12.027 | 117.826 |
| 本文方法 | -103.012 | -148.674 | -171.322 | 20.414 | 199.997 |
(4)分析对比
等效荷载法是用一组等效荷载代替有效预应力对结构的作用,可以正确地反映结构在有效预应力作用下的初始状态,即等效荷载法的节点位移、杆件轴力是在预设预应力状态下的正确值。但由于结构中没有预应力筋,预应力筋没有与混凝土一起参与结构的后期受力,当进一步加载时,此模型计算结果显然与实际情况不相符合。
计算结果可以看出,不计弹性收缩实体力筋法,即用式(1)换算的温度降幅在23杆产生的实际轴力只有117.826 kN,即58.913 MPa,并未达到预设的100 MPa,也就是说最终的预应力与预设有效预应力存在差异,5节点位移也和等效荷载法的结果间存有很大差异,说明这种模拟不能和预设效果相符,没有能够准确地模拟有效预应力下的结构力学状态。
考虑弹性收缩的实体力筋法,即用式(3)换算的等效降温在23杆产生的实际轴力几乎和预设应力100 MPa对应的轴力200 kN一致,两者误差仅为0.001 5%,节点位移结果也和等效荷载法下的几乎一致,说明此法可以正确模拟结构在有效预应力下的受力状态,且结构中含有力筋单元,与混凝土一起参与结构的后期受力,当进一步加载时,此模型能计算出与实际情况相符的结果。
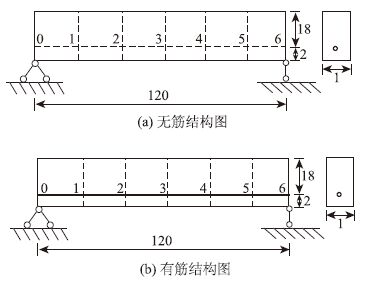
3.2 平面问题对图 3所示的平面简支梁问题,结构尺寸1.2 m×0.2 m,厚度取0.01 m,混凝土弹性模量Ec=2e10 Pa,泊松比μc=0.166 7,现欲在离下边界0.02 m处张拉一根预应力筋,筋截面面积A=0.000 1 m2,钢筋弹性模量Es=2e11Pa,泊松比μs=0.3,材料的热膨胀系数为α=1.0e-5 ℃-1。筋单元6等分,设从左至右各段的预设张拉应力分别为200,210,220,230,230,250 MPa。现用3种方法(平面单元均采用四节点单元)模拟结构预应力筋张拉后的力学状态。
|
| 图 3 平面简支梁结构示意图(单位:cm) Fig. 3 Plane simply supported beam structure(unit:cm) |
(1)采用等效荷载法,结构计算模型见图 3(a),混凝土单元网格划分如虚线示意。根据预应力等效的相对张拉力F=Aσ,可知应该施加在混凝土节点0上的集中力荷载为20 kN,方向向右;施加在节点1,2,3,4,5上的集中力荷载为1 kN,方向向右;施加在节点6上的集中力荷载为25 kN,方向向左。
(2)采用实体力筋法,钢筋处理为嵌入混凝土的桁架单元,计算模型见图 3(b)。用式(1)可得各段筋单元的降温荷载值为100,105,110,115,120,125 ℃。
(3)本文方法,采用计算模型3(b),由等效荷载法的位移结果计算得到的力筋01至56节点间总应变值分别为-0.001 19,-0.001 215,-0.001 28,-0.001 34,-0.001 385,-0.001 495,用式(3) 计算得考虑弹性收缩的相应降温荷载值ΔT′为:-219,-226.5,-238,-249,-258.5,-274.5 ℃。
计算结果见表 3、表 4。
| 节点号 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 等效荷载法 | -0.087 | -0.325 | -0.568 | -0.824 | -1.092 | -1.369 | -1.668 |
| 实体力筋法 | -0.040 06 | -0.148 9 | -0.261 5 | -0.379 8 | -0.503 5 | -0.632 2 | -0.768 2 |
| 本文方法 | -0.087 | -0.325 | -0.568 | -0.824 | -1.092 | -1.369 | -1.668 |
| 筋单元号 | 01 | 12 | 23 | 34 | 45 | 56 |
| 力筋应力 预设值 | 200 | 210 | 220 | 230 | 240 | 250 |
| 实体力筋法 | 91.194 | 97.368 | 101.707 | 106.317 | 111.319 | 113.921 |
| 本文方法 | 199.688 3 | 210.070 4 | 220.050 9 | 230.184 | 239.852 6 | 250.131 3 |
(4)分析对比
从计算结果可看出,对不计弹性收缩的实体力筋法,根据有效预应力换算的温度降低,产生的节点位移和等效荷载法的结果存有很大差异,在01筋单元至56筋单元上实际产生的应力未达到预设值,没有能准确地模拟出有效预应力状态。
对考虑弹性收缩的实体力筋法,得到的各节点位移与等效荷载法计算结果一致,产生的预应力筋实际应力值和预设有效预应力值误差很小,表明了本方法对于平面问题有效预应力模拟的正确性。
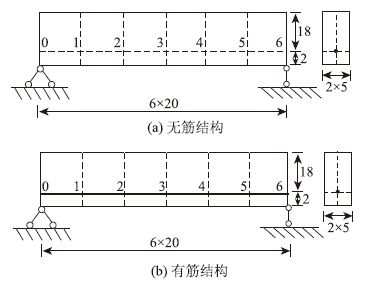
3.3 空间问题对图 4所示的空间简支梁问题,结构尺寸1.2 m×0.2 m×0.1 m,混凝土弹性模量Ec=2e10 Pa,泊松比μc=0.166 7,现欲在离下边界0.02 m,厚度中间位置处张拉一根预应力筋,筋截面面积A=0.000 1 m2,钢筋弹性模量Es=2e11Pa,泊松比μs=0.3,材料的热膨胀系数为α=1.0e-5 ℃-1。设力筋01段、12段、23段、34段、45段、56段的有效张拉应力分别为200,210,220,230,240,250 MPa,同上进行3种建模方法的模拟对比分析。
|
| 图 4 空间简支梁结构示意图(单位:cm) Fig. 4 Structure of space simple supported beam (unit:cm) |
(1)等效荷载法,结构计算模型为图 4(a),虚线为混凝土单元划分情况。同平面问题计算得在混凝土节点0上的集中力荷载为20 kN,方向向右;施加在节点1,2,3,4,5上的集中力荷载为1 kN,方向向右;施加在节点6上的集中力荷载为反方向25 kN。
(2)采用实体力筋法,计算模型为图 4(b)。用式(1)可得各段筋单元的降温荷载值为100,105,110,115,120,125 ℃。
(3)采用本文方法,仍然采用计算模型4(b),由等效荷载法的位移结果计算得到的力筋01至56节点间总应变值分别为-0.000 140 275,-0.000 12,-0.000 125,-0.000 135,-0.000 135,-0.000 18,用式(3) 计算得考虑弹性收缩的力筋相应降温荷载值ΔT′为:-114.027 5,-117,-122.5,-128.5,-133.5,-143 ℃。
计算结果见表 5、表 6。
| 节点号 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 等效荷载法 | -0.004 945 | -0.033 | -0.057 | -0.082 | -0.109 | -0.136 | -0.172 |
| 实体力筋法 | -0.004 519 | -0.029 23 | -0.050 31 | -0.073 32 | -0.097 43 | -0.121 4 | -0.152 7 |
| 本文方法 | -0.004 957 | -0.033 | -0.057 | -0.082 | -0.109 | -0.136 | -0.172 |
| 筋单元号 | 01 | 12 | 23 | 34 | 45 | 56 |
| 力筋应力 | 200 | 210 | 220 | 230 | 240 | 250 |
| 实体力筋法 | 175.292 4 | 188.918 9 | 196.986 8 | 205.888 4 | 216.078 3 | 218.675 7 |
| 本文方法 | 199.816 6 | 210.581 | 219.373 1 | 230.018 8 | 240.515 7 | 250.068 2 |
(4)分析对比
对比计算结果的结论同平面问题,对不计弹性收缩的实体力筋法,根据有效预应力换算的温度降低,产生的节点位移和等效荷载法的结果存有很大差异,在01筋单元至56筋单元上实际产生的应力未达到预设值,没有准确地模拟出有效预应力效果。
对考虑弹性收缩的实体力筋法,得到的各节点位移与等效荷载法计算结果一致,预应力筋的实际应力值和预设的有效预应力值吻合很好,表明了本方法对于空间问题有效预应力结构模拟的准确性。
4 结论
本文通过研究预应力模拟的等效荷载法和实体力筋法,提出了考虑混凝土弹性收缩引起预应力损失的等效温度计算公式,通过无筋模型和有筋模型的两次建模计算,以达到准确模拟预设预应力加载状态目的。该实体力筋法能在多种有限元通用软件中得以实现,通过实例验证计算,结果表明该方法简便实用,能实现有筋模型中有效预应力的准确模拟,为真实模拟预应力混凝土结构张拉加载、后续加载的受力分析,提供了又一种有效的方法。
| [1] | SHUSHKEWICH K W. Simplified Equivalent Loads of Prestressing[J]. |
| [2] | KUYUCULAR A. Prestressing Optimization of Concrete Slabs[J]. |
| [3] | 张道明,梁力,尹新生,等.预应力内荷载的新计算方法——直接内载法[J].工程力学,2007,24(3):104-109. ZHANG Dao-ming, LIANG Li, YIN Xin-sheng, et al. New Approach to Calculate Prestressed Internal Load: Direct Internal Load Method[J]. Engineering Mechanics, 2007,24(3):104-109. |
| [4] | 熊欢,李鹏辉,李庆斌,等.PCCP受载响应分析中三种预应力施加方法的比较研究[J].水力发电学报, 2010,29(6):178-186. XIONG Huan, LI Peng-hui, LI Qing-bin,et al. Comparative Study of Three Methods for the Prestressing Simulation in the Analysis of Load-bearing Response of a PCCP[J]. Journal of Hydroelectric Engineering, 2010,29(6):178-186. |
| [5] | 牛黎明.预应力等效荷载计算方法研究[J].交通科技,2012,254(5):12-14 NIU Li-ming. Study on Calculation Method of Prestressed Equivalent Load[J]. Transportation Science & Technology, 2012,254(5):12-14. |
| [6] | 黄侨,杨大伟,李忠龙.预应力混凝土梁桥的NURBS预应力束模型研究[J].公路交通科技,2007,27(1):51-54. HUANG Qiao, YANG Da-wei, LI Zhong-long. NURBS Strand Model for Prestressed Concrete Girder Bridges[J]. Journal of Highway and Transportation Research and Development,2007,27(1): 51-54. |
| [7] | 陈玉峰.用ANSYS进行预应力加载时解决损失的方法[J].四川建筑,2004,24(6):106. CHEN Yu-feng. Methods of Solving Prestressing Loss Applying ANSYS[J]. Sichuan Architecture, 2004,24(6):106. |
| [8] | 袁明,颜东煌.PC箱梁竖向预应力张拉锚固阶段应力损失研究[J].公路交通科技, 2010,27(10):53-57. YUAN Ming, YAN Dong-huang. Study on Vertical Prestress Loss of PC Box Girder during Stretching and Anchoring Stage[J]. Journal of Highway and Transportation Research and Development, 2010,27(10): 53-57. |
| [9] | 陈宜言,林松,尧国皇.有限元分析中钢筋混凝土梁的预应力模拟[J].深圳土木与建筑,2009,6(3):22-24. CHEN Yi-yan, LIN Song, YAO Guo-huang. Prestress Simulation of Steel Reinforced Concrete Bridge in Finite Element Analysis[J]. Shenzhen Civil Engineering and Architecture, 2009,6(3):22-24. |
| [10] | 刘烈坤,傅少君,田波.小湾拱坝放空底孔预应力闸墩三维有限元分析[J].武汉大学学报:工学版,2009,42(3):340-343. LIU Lie-kun, FU Shao-jun, TIAN Bo. 3D Finite Element Analysis of Prestressed Pier of Emptying Bottom Outlets in Xiaowan Arch Dam[J]. Engineering Journal of Wuhan University, 2009,42(3):340-343. |
| [11] | 李文华,贺拴海,翟晓亮,等.大跨径梁桥墩顶块空间应力数值分析及优化设计[J].长安大学学报:自然科学版,2011,31(4):50-57. LI Wen-hua,HE Shuan-hai, ZHAI Xiao-liang,et al. Numerical Analysis and Optimal Design for Block on Pier Top of Long Span Beam Bridge [J].Journal of Chang'an University: Natural Science Edition, 2011,31(4):50-57. |
| [12] | 陈军,周安,詹炳根,等.曲线箱梁桥预应力筋张拉顺序的数值模拟及优化[J].工程与建设,2011,25(1):1-3. CHEN Jun,ZHOU An,ZHAN Bing-gen. Numerical Simulation and Optimization of Prestressed Tensioning Sequence of Curve Box Girder Bridge[J]. Engineering and Construction, 2011,25(1): 1-3. |
| [13] | 周江.用等效温度荷载法直接计算预应力混凝土结构的次内力[J].建筑结构, 2013,43(增2):572-575. ZHOU Jiang. Directly Calculating Secondary Interior Forces of Pre-stressed Concrete Structures with Equivalent Temperature Load Method[J]. Building Structure, 2013,43(S2):572-575. |
| [14] | 刘轲,赵建昌.某预应力混凝土简支梁降温法的有限元分析[J].山西建筑,2008,34(5):92-93. LIU Ke,ZHAO Jian-chang. Finite Element Analysis on the Prestressed Concrete Simple Beam with the Cooling Method[J].Shanxi Architecture, 2008,34(5):92-93. |
| [15] | 宁俊超.基于ansys大跨度张弦梁结构预应力模拟研究[D].成都:西南交通大学,2013. NING Jun-chao. Simulation of Prestressed Long-span Beam String Structure Based on Ansys[D].Chengdu: Southwest Jiaotong University, 2013. |
 2015, Vol. 31
2015, Vol. 31
