扩展功能
文章信息
- 刘世明, 刘永健, 琚明杰
- LIU Shi-ming, LIU Yong-jian, JU Ming-jie
- 无背索曲塔曲梁斜拉桥施工优化
- Construction Optimization of Curved-pylon and Curved-girder Cable-stayed Bridge without Back Stay
- 公路交通科技, 2015, Vol. 31 (11): 68-74,80
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (11): 68-74,80
- 10.3969/j.issn.1002-0268.2015.11.011
-
文章历史
- 收稿日期: 2015-02-10
2. 长安大学 旧桥检测与加固技术交通行业重点实验室, 陕西 西安 710064;
3. 东莞市交通投资集团有限公司, 广东 东莞 523120
2. Key Laboratory for Bridge Detection and Reinforcement Technology of Ministry of Transport, Chang'an University, Xi'an Shaanxi 710064, China;
3. Dongguan Communications Investment Group Co., Ltd., Dongguan Guangdong 523120, China
随着社会经济的快速发展和人们对桥梁景观的高水平追求,无背索斜拉桥以其独特的造型受到人们的喜爱,在我国建设的数量已达20座[1]。正确合理的斜拉桥施工顺序、索力大小对结构安全、施工方便、工程造价等有重要的影响。文献[2, 3, 4, 5, 6]分别对悬臂施工、支架施工斜拉桥的索力大小及更换顺序、施工顺序等进行了优化研究。文献[7, 8, 9]进行了施工过程精细化的仿真分析,确保了施工安全,明确各构件传力状态。纵观已建无背索斜拉桥的桥塔、主梁大都采用直线布置,桥塔、主梁均采用曲线布置时,结构受力复杂,施工工艺、要求及顺序影响因素多。文献[10, 11, 12, 13]研究了东莞水道桥的结构选型、受力模式和设计优化,而没有开展施工优化研究,目前尚没有针对性的施工技术规范条款,有必要开展相关研究工作。本文结合东莞水道桥的施工监控及相关科研工作,以不改变拉索类型、施工简便可行、成桥状态受力合理为控制目标,尽可能使结构受力合理、缩短工期、节省工程造价,对设计图纸施工顺序进行优化调整,为确定合理的桥梁施工顺序提供依据。
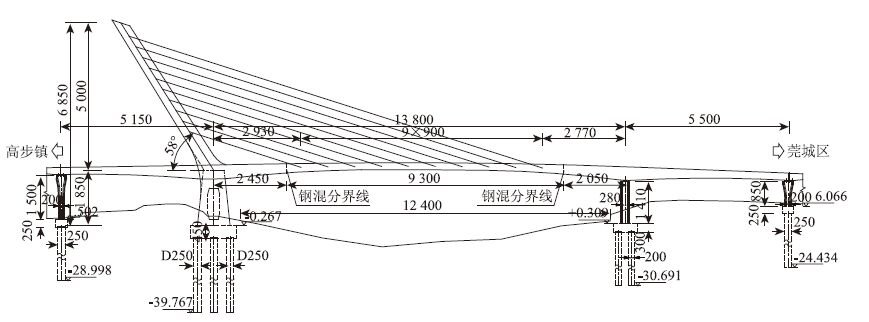
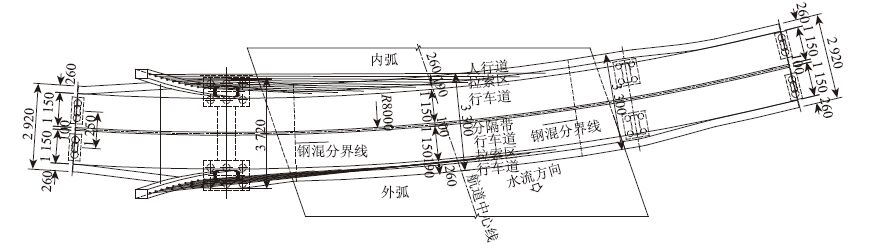
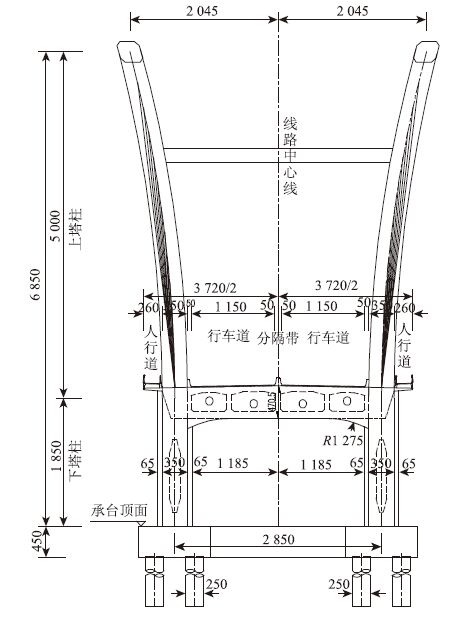
1 桥梁结构分析 1.1 桥梁概况东莞水道桥平面位于半径为800 m圆曲线上,小桩号侧纵坡为1.68%,大桩号侧纵坡为-4%,竖曲线半径为2 000 m。采用塔梁墩固结体系无背索曲塔曲梁斜拉桥,跨径布置为(51.5+138+55) m[14]。桥梁立面、平面和桥塔处横断面如图 1~图 3所示。
|
| 图 1 桥梁立面图(单位:cm) Fig. 1 Elevation view of bridge (unit: cm) |
|
| 图 2 桥梁平面图(单位:cm) Fig. 2 Plan view of bridge (unit: cm) |
|
| 图 3 桥塔处横断面图(单位:cm) Fig. 3 Sectional view at pylon of bridge (unit: cm) |
主塔位于车行道与人行道之间,每个主塔横桥向宽3~3.5 m,顺桥向宽4~5.5 m,主塔横桥向往外圆弧张开,顺桥向水平倾角为58°。上塔柱采用预应力钢箱混凝土结构,在内外钢箱内填充C50微膨胀混凝土,每个塔柱13个节段,采用悬臂拼装施工。下塔柱为变截面空心普通钢筋混凝土结构。两塔柱间设两道横向备用拉索,离桥面垂直距离分别为34.506,31.894 m。横向备用拉索规格为GJ15-3,锚固于塔柱侧壁。
主梁采用钢混凝土混合梁,主跨中间一段93 m为钢箱梁,采用变截面梁高2.3~3.014 m,两头各设一个钢混结合段。边跨为变截面斜腹板混凝土梁,梁高2.3~4.5 m。桥面标准宽度为33 m,桥塔位置处加宽至37.2 m,55 m边跨桥宽由29.2 m变宽至33 m,51.5 m边跨桥宽由37.2 m变化至29.2 m。
拉索采用竖琴式双索面布置,钢梁上索距为9.0 m,拉索水平夹角为18°,共计20根拉索,采用桥塔端张拉。
1.2 结构特点与常规的无背索斜拉桥相比,东莞水道桥在结构形式、受力特点和施工方法上都有其独创性和新颖性,其主要特点有:
(1)桥梁纵坡较大,最大纵坡达4%,在理论计算和施工控制难度大。
(2)曲塔、曲梁及拉索间空间力学行为复杂,曲塔、曲梁受力状态为压、弯、剪及扭转联合作用,各作用间相互耦合,理论分析难度大。
(3)钢混结合段位于曲线上,结合段的受力状态、传力机理复杂。
(4)悬臂拼装变宽变高曲梁、曲塔,节段需要进行空间定位,施工控制难度大,特别是曲塔,5个格室空间均较小,布置有预应力及拉索锚板、PBL连接件和普通钢筋,施工空间小,各节段间混凝土面为倾斜的且高差比较大,混凝土浇注困难,浇注质量难以控制。
(5)箱梁宽度达29.2~37.2 m,剪力滞效应明显。
1.3 施工顺序设计图纸采用满堂支架和悬臂拼装法相结合的施工方法,其主要施工顺序如下:
(1)桥梁桩基础、承台、墩身、主塔下塔柱及节段1施工。
(2)搭设预应力混凝土及钢混结合段处支架,预压处理,浇注相应混凝土,预埋钢构件,张拉预应力钢筋。
(3)安装桥面吊机,悬臂安装各箱梁梁段,其中小桩号侧4个节段,大桩号侧5个节段。
(4)主跨主梁合龙,拆除桥面吊机。
(5)悬拼主塔节段2、3,灌注塔内混凝土、张拉预应力钢筋及拉索1,依次悬臂安装主塔4~13节段,灌注塔内混凝土、张拉预应力钢筋及对应拉索。
(6)张拉塔间横向拉索。
(7)拆除支架,安装桥面附属结构,桥面系施工。
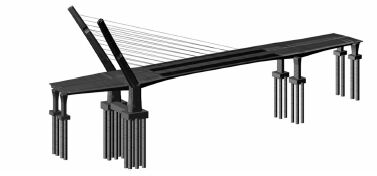
2 桥梁施工优化比选 2.1 有限元模型在充分理解设计图纸的基础上,考虑桥梁平弯、纵横坡、材料、施工过程及桥位处地质信息等,采用MIDAS/CIVIL有限元程序建立了全桥的空间分析模型,其中,主塔、主梁、桩基础、墩身、承台等采用梁单元模拟,拉索采用桁架单元模拟,并按Ernst公式对弹性模量进行修正。模型共计1 080个节点,1 035个单元,6种材料属性,混凝土的收缩、徐变作用按《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTGD 62—2004)计算,混凝土的强度发展采用1990年欧洲混凝土规范(CEB-FIP)计算。主要边界条件:主塔钢箱及混凝土部分采用双主梁单元、共节点模拟,不计两者间的相对位移;钢混结合的采用共节点模拟,其中实心混凝土部分作为外荷载施加;支架采用只受压节点弹簧模拟;桩土相互作用采用等代节点弹簧模拟;主梁与支座上节点、承台与桩基础、拉索与塔梁均采用为刚性连接的主从约束模拟,桥梁支座用弹性支承等代弹簧模拟;主梁与塔采用弹性连接中的刚性连接模拟。根据施工方案,全桥共分为49个施工阶段。三维有限元整体计算模型见图 4。
|
| 图 4 桥梁计算模型 Fig. 4 Computation model of bridge |
在已有设计图纸施工方法和施工顺序的基础上,依据成桥结构受力合理、安全、施工方便、节省工程投资和缩短工期等原则,对施工顺序进行优化如下:
(1)主梁在支架施工完成后,拆除主梁下支架,然后再进行钢主梁悬臂拼装的施工,这样悬臂拼装施工时受力更明确,同时缩短了支架使用时间,提高周转效率,节省工程投资。
(2)桥塔3节段前施工顺序与原设计一致,而在4~7节段主塔施工时,与对应的主梁节段同时悬拼施工,并张拉对应位置处的斜拉索,这样主塔和主梁同步悬臂施工,加快了施工进度,缩短施工工期。
2.3 优化前后应力和变形分析不改变主塔、主梁预应力钢筋类型及布置形式,以成桥状态为目标索力调整拉索初拉力,采用优化后的施工顺序调整理论计算模型,与优化前的计算结果进行对比,分析对结构受力性能的影响。
(1)主塔的应力和变形分析
因主塔采用钢箱混凝土结构,不同的施工顺序时,成桥时主塔应力和变形是有差别的,优化前后主塔钢箱、混凝土特征截面的正应力见表 1和表 2,其中括号内、外数据分别为对应位置处内、外弧侧主塔的应力;优化前后主塔位移见表 3,其中坐标轴x方向为桥塔位置处桥面沿行车水平方向,y方向为圆心方向,z方向为竖直向上,下同。
| 位置 | 节段1底 | 节段3底 | 节段5底 | 节段7底 | 节段9底 | 节段11底 | 节段13底 |
| 原设计外侧上缘 | -40.8(-31.0) | -23.2(-42.8) | -77.2(-35.1) | -54.7(-32.4) | -39.4(-21.7) | -25.2(-11.1) | -0.4(-0.4) |
| 优化后外侧上缘 | -40.8(-31.1) | -22.1(-41.3) | -75.6(-34.1) | -53.0(-31.3) | -38.2(-21.0) | -24.2(-10.5) | 0.0(0.0) |
| 差值 | 0.0(-0.1) | 1.1(1.5) | 1.6(1.0) | 1.7(1.1) | 1.2(0.7) | 1.0(0.6) | 0.4(0.4) |
| 原设计内侧上缘 | -63.8(-50.3) | -16.1(-17.8) | -57.5(-58.8) | -41.1(-36.2) | -27.1(-17.9) | -13.3(-11.9) | -0.4(-0.4) |
| 优化后内侧上缘 | -65.2(-51.9) | -15.1(-16.4) | -56.5(-58.0) | -40.1(-35.3) | -26.2(-17.3) | -12.6(-11.3) | 0.0(0.0) |
| 差值 | -1.4(-1.6) | 1.0(1.4) | 1.0(0.8) | 1.0(0.9) | 0.9(0.6) | 0.7(0.6) | 0.4(0.4) |
| 原设计内侧下缘 | -60.6(-61.8) | -82.3(-52.8) | -22.8(-53.1) | -30.9(-41.3) | -25.7(-33.1) | -20.1(-26.9) | -4.2(-4.2) |
| 优化后内侧下缘 | -61.7(-62.8) | -81.0(-52.2) | -21.6(-51.8) | -29.8(-40.0) | -24.9(-32.2) | -19.3(-25.9) | -3.8(-3.8) |
| 差值 | -1.1(-1.0) | 1.3(0.6) | 1.2(1.3) | 1.1(1.3) | 0.8(0.9) | 0.8(1.0) | 0.4(0.4) |
| 原设计外侧下缘 | -37.6(-42.5) | -89.3(-77.8) | -42.5(-29.4) | -44.5(-37.5) | -38.0(-37.0) | -32.0(-26.1) | -4.3(-4.3) |
| 优化后外侧下缘 | -37.3(-42.0) | -88.0(-77.2) | -40.8(-27.9) | -42.8(-36.0) | -36.9(-35.9) | -30.9(-25.1) | -3.8(-3.8) |
| 差值 | 0.3(0.5) | 1.3(0.6) | 1.7(1.5) | 1.7(1.5) | 1.1(1.1) | 1.1(1.0) | 0.5(0.5) |
| 位置 | 节段1底 | 节段3底 | 节段5底 | 节段7底 | 节段9底 | 节段11底 | 节段13底 |
| 原设计外侧上缘 | -5.0 (-3.7) | -3.9(-1.9) | -3.7(-1.8) | -4.2(-2.2) | -3.4(-1.5) | -2.4(-1.0) | 0.1(0.1) |
| 优化后外侧上缘 | -5.0(-3.7) | -3.9(-1.9) | -3.8(-1.8) | -4.3(-2.2) | -3.4(-1.5) | -2.4(-1.0) | 0.1(0.1) |
| 差值 | 0.0(0.0) | 0.0(0.0) | 0.0(0.0) | -0.1(0.0) | 0.0(0.0) | 0.0(0.0) | 0.0(0.0) |
| 原设计内侧上缘 | -7.5(-5.8) | -5.3(-4.4) | -3.4(-2.7) | -2.6(-2.1) | -1.4(-1.2) | -1.2(-1.1) | 0.1(0.1) |
| 优化后内侧上缘 | -7.4(-5.8) | -5.3(-4.4) | -3.4(-2.7) | -2.6(-2.1) | -1.4(-1.2) | -1.2(-1.1) | 0.1(0.1) |
| 差值 | 0.1(0.0) | 0.0(0.0) | 0.0(0.0) | 0.0(0.0) | 0.0(0.0) | 0.0(0.0) | 0.0(0.0) |
| 原设计内侧下缘 | -6.3(-6.4) | -6.1(-7.0) | -5.1(-6.1) | -3.8(-4.6) | -2.7(-3.5) | -1.7(-2.4) | -0.1(-0.1) |
| 优化后内侧下缘 | -6.3(-6.4) | -6.2(-7.1) | -5.2(-6.2) | -3.9(-4.7) | -2.7(-3.5) | -1.8(-2.4) | -0.1(-0.1) |
| 差值 | 0.0(0.0) | -0.1(-0.1) | -0.1(-0.1) | -0.1(-0.1) | 0.0(-0.1) | 0.0(0.0) | 0.0(0.0) |
| 原设计外侧下缘 | -3.8(-4.3) | -4.7(-4.6) | -5.1(-5.5) | -5.4(-4.8) | -4.6(-3.8) | -2.9(-2.3) | -0.1(-0.1) |
| 优化后外侧下缘 | -3.9 (-4.4) | -4.8(-4.6) | -5.2(-5.6) | -5.5(-4.8) | -4.7(-3.8) | -2.9(-2.3) | -0.1(-0.1) |
| 差值 | -0.1(-0.1) | -0.1(-0.1) | -0.1(-0.1) | -0.1(0.0) | -0.1(0.0) | 0.0(0.0) | 0.0(0.0) |
| 位置 | 节段1顶 | 节段3顶 | 节段5顶 | 节段7顶 | 节段9顶 | 节段11顶 | 节段13顶 |
| 原设计x方向 | 4.5(4.7) | 0.3(-0.9) | 4.3(1.1) | 8.6(3.1) | 11.7(4.4) | 15.4(7.4) | 8.8(8.3) |
| 优化后x方向 | -1.9(-1.8) | 6.1(4.9) | -7.2(-10.2) | 0.5(-4.5) | 11.7(5) | 15.9(8.4) | 9.6(9.6) |
| 差值 | -6.4(-6.5) | 5.8(5.7) | -11.5(-11.3) | -8(-7.6) | 0(0.6) | 0.4(0.9) | 0.8(1.3) |
| 原设计y方向 | 2.1(-0.6) | 5.7(-4.9) | 4.2(-4) | -8.2(6.8) | -22.5(21.9) | -26.3(21.4) | 4.2(-1.3) |
| 优化后y方向 | 2.2(-0.7) | 6(-5.2) | 4.3(-4) | -9(7.7) | -23.3(23.3) | -26.4(22.1) | 4.3(-0.8) |
| 差值 | 0.1(-0.1) | 0.3(-0.3) | 0.1(0.1) | -0.8(0.9) | -0.8(1.4) | -0.2(0.8) | 0.2(0.4) |
| 原设计z方向 | -17.9(-18.2) | -8.2(-8.9) | -7.5(-9.1) | -6.9(-9.5) | -6.9(-10.5) | -5(-8.3) | -0.4(-0.9) |
| 优化后z方向 | -19(-19.2) | -8.4(-9.1) | -11.8(-13.4) | -9.9(-12.2) | -6.4(-9.8) | -4.2(-7.4) | 0.6(0.2) |
| 差值 | -1(-1) | -0.2(-0.2) | -4.4(-4.3) | -2.9(-2.7) | 0.5(0.7) | 0.7(0.9) | 0.9(1.1) |
由表 1可知,优化前后桥塔钢箱应力变化规律一致,均处于受压状态,受施工方法、混凝土收缩徐变及预应力钢筋等影响,在节段接口处存在突变,主塔钢箱应力在底部较大,向上逐渐增大,并在节段3底部达到最大,随后向上逐渐减少;截面上、下缘的内、外侧应力差异较大,表明曲塔空间弯曲效应明显;因曲梁布置形式的影响,内、外弧侧桥塔钢箱应力分布差异较大,不对称性明显,外侧主塔受力较不利;优化前后除节段1底部上缘及内侧下移应力值增大外,其余节段位置处应力均有所减少,应力变化值均很小,增大最值为1.6 MPa,减少最值为1.7 MPa,优化后成桥阶段主塔钢箱受力较合理。
由表 2可知,优化前后桥塔混凝土应力变化规律一致,均处于受压状态,外侧塔混凝土最大压应力出现在节段1底部内侧上缘截面,内侧桥塔混凝土最大压应力出现在节段3底部内侧下缘;截面上、下缘的内、外侧应力表现较大的差异表明曲塔空间弯曲效应明显;因曲梁布置形式的影响,内、外弧侧桥塔混凝土应力分布存在一定差异,差值最大出现在节段3、节段5底部位置,不对称性明显;优化前后主塔混凝土应力变化量很小,最大差值为0.1 MPa,表明优化施工顺序对桥塔混凝土应力的影响可以忽略不计。
由表 3可知,优化前后桥塔x、y方向变形均较小,最值不在塔顶位置,且内、外弧侧桥塔变形分布存在一定差异,不对称性明显;优化前后主塔x,y方向位移变化量很小,最大差值分别为11.5,1.4 mm,x方向最大差值发生在节段5顶部,表明优化施工顺序对桥塔x方向的位移影响较大;优化前后桥塔z方向变形最值均发生在节段1顶部,变化量很小,最大差值为4.4 mm,发生在节段5顶部位置。
(2)主梁的应力和变形分析
为研究施工顺序优化前后对主梁的影响,对成桥阶段的应力和变形进行分析,主梁特征截面处的正应力见表 4,主梁的特征变形见表 5,表中39#墩为主塔处桥墩,40#墩为主跨与右侧边跨之间的桥墩。
| 位置 | 左边跨跨中 | 39#墩处 | 主跨1/4跨径 | 主跨跨中 | 主跨3/4跨径 | 40#墩处 | 右边跨跨中 |
| 原设计外侧上缘 | -4.3 | -1.6 | 37.6 | 0.3 | 46.4 | -5.5 | -7.5 |
| 优化后外侧上缘 | -4.7 | -2.4 | 15.6 | -10.6 | 50.0 | -5.1 | -6.8 |
| 差值 | -0.4 | -0.8 | -22.0 | -10.9 | 3.6 | 0.4 | 0.7 |
| 原设计内侧上缘 | -4.3 | -1.6 | 33.9 | -1.3 | 47.2 | -5.5 | -7.2 |
| 优化后内侧上缘 | -4.7 | -2.4 | 11.3 | -12.6 | 50.6 | -5.1 | -6.5 |
| 差值 | -0.4 | -0.8 | -22.6 | -11.4 | 3.4 | 0.5 | 0.7 |
| 原设计内侧下缘 | -6.9 | -7.1 | -110.0 | -20.2 | -98.0 | -7.9 | -9.6 |
| 优化后内侧下缘 | -6.4 | -6.2 | -66.5 | 2.2 | -105.0 | -8.5 | -10.7 |
| 差值 | 0.5 | 0.9 | 43.5 | 22.4 | -7.0 | -0.6 | -1.1 |
| 原设计外侧下缘 | -6.9 | -7.1 | -107.0 | -19.0 | -98.7 | -8.0 | -9.8 |
| 优化后外侧下缘 | -6.4 | -6.2 | -63.2 | 3.8 | -106.0 | -8.5 | -10.9 |
| 差值 | 0.5 | 0.9 | 43.8 | 22.8 | -7.3 | -0.6 | -1.1 |
| 位置 | 左边跨跨中 | 主跨1/4跨径 | 主跨跨中 | 主跨3/4跨径 | 右边跨跨中 |
| 原设计x方向 | 11.8 | 2.2 | -10.7 | -26.0 | -26.3 |
| 优化后x方向 | 7.0 | -3.1 | 1.5 | -19.8 | -14.5 |
| 差值 | -4.8 | -5.3 | 12.2 | 6.3 | 11.7 |
| 原设计y方向 | 1.0 | -0.1 | -1.1 | -2.6 | -5.1 |
| 优化后y方向 | 0.9 | -0.1 | -0.2 | -1.9 | -2.7 |
| 差值 | -0.1 | 0.0 | 0.9 | 0.7 | 2.4 |
| 原设计z方向 | -8.1 | -35.6 | 23.2 | -66.2 | -11.0 |
| 优化后z方向 | -12.3 | -11.0 | -16.6 | -99.4 | -2.9 |
| 差值 | -4.2 | 24.7 | -39.8 | -33.2 | 8.1 |
由表 4可知,优化前后主梁混凝土部分上、下缘的内、外侧应力差别较小,钢主梁部分变化大,表明曲梁引起的混凝土主梁扭转效应不明显,钢主梁扭转效应明显。优化施工顺序后,主梁受力表现如下特点:左边跨上缘压应力有所增大,下缘压应力有所减少,右边跨与之相反,最大差值为1.1 MPa,对主梁整体受力影响较小;主跨1/4跨径处的应力有明显的下降,最大差值达43.8 MPa,主跨3/4跨径处的应力有稍微增加,最大差值为7.3 MPa;主跨跨中上缘应力有所增大,下缘应力值有所减少,但整体的应力水平比较小,不控制设计计算;钢主梁应力最大值比原设计低,与原设计相比,主梁整体受力状况得到一定程度的改善。
施工优化后,因拉索张拉时主梁未合龙,主梁整体刚度相对较低,故对变形影响较大。由表 5可知,优化后主梁位移的变化有如下特点:主梁x方向位移,除主跨1/4跨径处外,位移值均有所减少;主梁y方向变形趋势一致,位移值均有所减少,减少最大值为2.4 mm;主梁z方向位移在左边跨跨中、主跨3/4跨径处有所增加,其中3/4跨径处位置变化值较大,差值为33.2 mm,其他位置均有所减少;主梁的整体变形对结构线形的影响,通过设置预拱度来完成。
(3)拉索初拉力分析
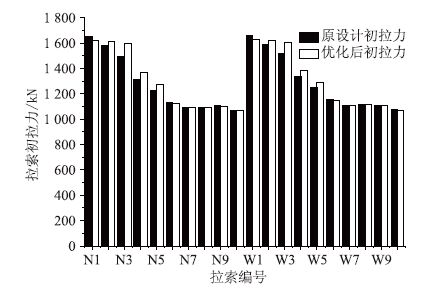
拉索采用一次张拉法控制施工时,为达到成桥设计索力值,不同的施工顺序,索力初张拉值会存在一定差异,优化前后的索力初张拉值如图 5所示,图中拉索编号为从桥塔侧依次为1~10,N表示内弧侧塔,W表示外弧侧塔。
|
| 图 5 优化前后拉索初拉力(单位:kN) Fig. 5 Initial forces of cable before and after optimization (unit: kN) |
由图 5可知,优化施工顺序后,2#~5#拉索初拉力均有所增大,最大差值为97.9 kN,增长率为6.5%,拉索安全系数的最小值为2.6,满足规范规程要求,其余索力均有稍微减少。索力值整体变化值不大,施工张拉设备与原设计一致。
3 结论建立了考虑施工阶段的有限元分析模型,对图纸原有施工顺序进行优化,分析比较优化前后主塔(包括钢箱和混凝土)应力和变形、主梁的应力及变形、拉索初拉力变化情况,研究表明:
(1)优化施工后,与常规斜拉桥悬拼施工类似,结构受力更明确,能缩短工期,节省工程投资。
(2)优化前后主塔应力分布规律一致,其中钢箱应力变化最值为1.7 MPa,混凝土应力变化最值为0.1 MPa,优化后钢箱受力更加合理,混凝土受力影响可忽略不计;优化前后内、外弧侧主塔位移不对称性明显,对桥塔x方向的位移影响较大,最大变化量为11.5 mm,y,z方向影响较小。
(3)优化后对混凝土主梁整体受力影响小,钢主梁整体受力状况得到一定程度的改善;因优化后拉索张拉时主梁刚度相对较低,主梁z方向位移在主跨3/4跨径处变化值较大,差值为33.2 mm,其他位置均有所减少,位移变化可以调整施工预拱度进行调整,x,y方向位移影响小。
(4)优化施工顺序后,2#~5#拉索初拉力均有所增大,最大差值为97.9 kN,增大率为6.5%,拉索安全系数的最小值为2.6,满足设计规范要求,其余索力均有稍微减少。
| [1] | 刘世明, 赵顺波,李晓克. 大跨人行异型斜拉桥静、动力及抗震性能分析[J].桥梁建设,2012,42 (4):45-50. LIU Shi-ming, ZHAO Shun-bo, LI Xiao-ke. Analysis of Static, Dynamic and Seismic Performance of Long Span Irregular-shape Pedestrian Cable-stayed Bridge[J]. Bridge Construction,2012, 42(4):45-50. |
| [2] | 戴宇文,王友元,何锦明. 混合式桥面体系斜拉桥悬臂施工优化[J]. 桥梁建设,2014,44 (4):117-121. DAI Yu-wen, WANG You-yuan, HE Jin-ming. Optimization of Cantilever Construction of CableStayed Bridge with Hybrid Deck System[J]. Bridge Construction,2014,44(4):117-121. |
| [3] | 王珊,方有亮. 同步优化斜拉桥施工索力及成桥索力的方法[J]. 四川建筑,2014,34(5):132-134. WANG Shan, FANG You-liang. Method of Simultaneous Optimization Cable Forces of Cable-stayed Bridge during Construction and Completion [J].Sichuan Architecture,2014,34 (5):132-134. |
| [4] | 付三伟,郑文通,王智勇,等. 独塔不对称斜拉桥压重施加顺序的优化研究[J]. 中外公路,2014 (4):205-207. FU San-wei, ZHENG Wen-tong, WANG Zhi-yong, et al. Optimization Study on Weight Applied Sequence of Single-pylon Asymmetric Cable-stayed Bridge[J]. Journal of China & Foreign Highway,2014 (4) : 205-207. |
| [5] | 史国刚,孙洪滨,吉伯海,等.基于灵敏度分析的斜拉桥拉索更换顺序研究[J].防灾减灾工程学报,2011,31(5):590-594. SHI Guo-gang,SUN Hong-bin,JI Bo-hai,et al. Study on Sequence of Cable Replacement for Cable-stayed Bridge Based on Sensitivity Analysis[J]. Journal of Diaster Prevention and Mitigation Engineering,2011,31(5):590-594. |
| [6] | 高立强,蒲黔辉,霍学晋,等.索梁组合体系桥梁施工索力确定的割线迭代法[J].公路交通科技,2012,29(6):81-86,92. GAO Li-qiang, PU Qian-hui, HUO Xue-jin, et al. Secant Iterative Method for Determining Construction Cable Forces of Combined-system Bridge with Cable and Girder[J]. Journal of Highway and Transportation Research and Development,2012, 29(6):81-86,92. |
| [7] | 莫亚南,彭成明. 大跨独塔部分斜拉钢桁梁桥施工仿真分析[J]. 公路交通技术,2014(6):97-102. MO Ya-nan, PENG Cheng-ming. Simulated Analysis for Construction of Large-span Single-tower Partially Cable-stayed Steel Truss Bridges[J]. Technology of Highway and Transport,2014(6):97-102. |
| [8] | 李旺,王解军,彭小亮. 矮塔斜拉桥施工过程非线性受力分析[J]. 公路工程,2014,39(2):205-206,226. LI Wang, WANG Jie-jun, PENG Xiao-liang. Nonlinear Analysis for Short Tower Cable-stayed Bridge in Construction[J]. Highway Engineering,2014,39(2):205-206,226. |
| [9] | 郑文通,王智勇,郭金山,等. 独塔不对称斜拉桥主梁施工中支架受力行为研究[J]. 中外公路,2014 (4):174-176. ZHENG Wen-tong, WANG Zhi-yong, GUO Jin-shan, et al. Research on Force Behavior of Girder Bracket of Single-pylon Asymmetric Cable-stayed Bridge during Construction [J]. Journal of China & Foreign Highway,2014 (4) : 174-176. |
| [10] | 杨敏.无背索曲塔曲梁斜拉桥的力学性能分析与研究[D].广州:广东工业大学,2012. YANG Min. Research on Curved-pylon and Curved-girder Cable-stayed Bridge without Back Stay [D].Guangzhou:Guangdong University of Technology,2012. |
| [11] | 盛捷.无背索曲塔曲梁斜拉桥力学性能分析与试验研究[D].长沙:湖南大学,2012. SHENG Jie. Mechanical Property Analysis and Experimental Research of Curved-pylon and Curved-girder Cable-stayed Bridge without Backstays[D].Changsha: Hunan University,2012. |
| [12] | 琚明杰.无背索曲塔曲梁斜拉桥受力性能研究[D].西安:长安大学,2011. JU Ming-jie. Analysis on Mechanical Performance of Curved-pylon and Curved-girder Cable-stayed Bridge without Backstays[D].Xi'an: Chang'an University,2011. |
| [13] | 朱强. 东莞市东江梨川大桥工程桥梁结构选型及景观设计[J]. 城市道桥与防洪,2011(6):65-69. ZHU Qiang. Selection of Bridge Structure and Design of Landscape for Dongwan City Dongjiang Lichuan Bridge Project[J]. Urban Roads Bridges & Flood Control, 2011(6):65-69. |
| [14] | 刘世明,刘永健.无背索曲塔曲梁斜拉桥参数敏感性分析[J].公路交通科技,2014,31(2):54-59. LIU Shi-ming, LIU Yong-jian. Analysis of Parameter Sensitivity for Curved-pylon and Curved-girder Cable-stayed Bridge without Back-stay[J]. Journal of Highway and Transportation Research and Development,2014, 31(2):54-59. |
 2015, Vol. 31
2015, Vol. 31
