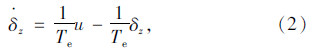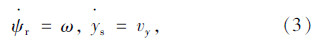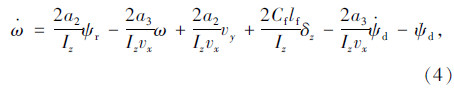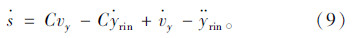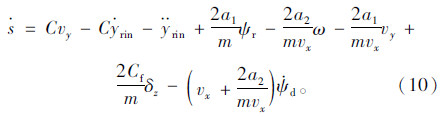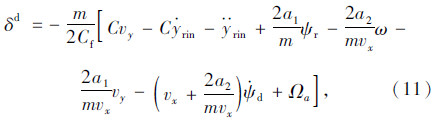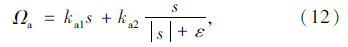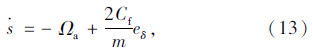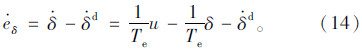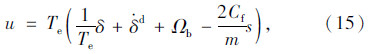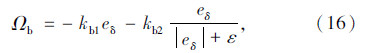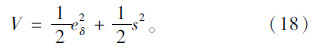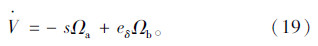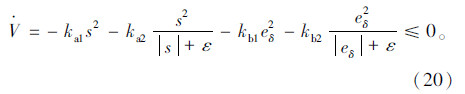扩展功能
文章信息
- 杨洁, 许宏科, 赵俊波, 雷军委
- YANG Jie, XU Kong-ke, ZHAO Jun-bo, LEI Jun-wei
- 基于反演与滑模的车道线横向位置复合控制研究
- Research on Hybrid Control of Lateral Position of Lane Line Based on Inversion and Sliding Mode
- 公路交通科技, 2015, Vol. 32 (10): 153-158
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 32 (10): 153-158
- 10.3969/j.issn.1002-0268.2015.10.025
-
文章历史
- 收稿日期: 2014-12-14
2. 长安大学, 陕西 西安 710064;
3. 海军航空工程学院, 山东 烟台 264001
2. Chang'an University, Xi'an Shaanxi 710064, China;
3. Naval Aeronautical and Astronautical University, Yantai Shandong 264001, China
近年来,车辆自主驾驶的相关技术引起了国内外学者的广泛兴趣。其中车道线保持控制是车辆自主驾驶的关键技术之一。它通过车辆在运行中对汽车相对车道线中心的偏移量,根据相应的控制算法计算方向盘转角的大小,从而控制车辆跟随车道线轨迹而安全行驶。文献[1, 2, 3, 4, 5, 6]针对二自由度前轮转向车辆横向动力学,考虑了车辆模型参数在运行中受外界扰动影响而产生的摄动,分别尝试采用自适应、模糊控制、神经网络与滑模控制的方法设计了横向位置偏差控制器,实现了车道线保持的车辆横向安全控制。
文献[7]在此基础上进一步考虑了车辆转向机构的动态特性,采用时间常数为0.1 s的一阶惯性环节来模拟转向机构的物理延迟特性,选用双级性sigmoid函数代替传统滑模控制中的符号函数,设计了自校正滑模控制器,改善了滑模控制器输出的抖振现象。该文献重点描述了切换增益与边界层厚度自校正律对消除系统抖振以及饱含环节减轻工作负荷的作用,但对转向机构动态特性对系统的不利影响及控制律设计中如何采取相应措施处理转向机构动态延迟没有深入分析。
转向机构动态延迟的引入,大大增加了系统设计与稳定性的难度。其一是增加了系统阶次,从而导致了设计与分析的复杂度增加。其二是以往文献采用滑模控制时,滑模面的构成均由横向位置偏差以及偏差的导数组成,即由位置与速度信息匹配,具有明显的物理意义,而新考虑的第3阶转向机构的动态特性,无论是把转向机构的转动角还是转动角速率引入滑模面,均难以和已有的车辆位置与速度信息匹配,而且设计将变得复杂。不易匹配的原因主要是由于位置与速度是描述车辆的信息,而转动角与转动角速率则是与转向机构物理特性相关的信息,两者难以构成相关的微分关系,因此难以组成滑模面。其三是也可在滑模面中引入横向位置偏差的二阶导数,即加速度信息,但这意味着需要引入车辆加速度测量传感器,这不仅增大了算法复杂度,而且增加了控制成本。
目前车辆保持面临的主要问题是控制器设计的强鲁棒性问题,主要是由于理论建模和实际试验的数据之间总是存在一定的差别,而该问题的解决在理论设计阶段只能从两方面解决: 一是建模尽量精确,二是针对理论模型使得算法具有极强的鲁棒性。只有具有强鲁棒性的控制器才会在未来试验中走得更远。本文基于以上思想,首先在模型上,进一步精确考虑转向机构的动态特性;其次在控制器设计上着重考虑其鲁棒性的提高;最后在数字仿真验证上,也采用多次重复随机仿真来严格检验反演滑模控制器的鲁棒性。
综合以上分析,本文提出一类反演滑模复合控制方法,保留原有滑模面的组成形式,采用滑模控制方法将车辆运动动力学模型降阶为一阶,与引入的转向机构的一阶惯性特性组成二阶系统,采用反演控制层层倒推的方法,根据Lyapunov理论设计新组成二阶系统的控制律,实现车道线横向位置偏差的安全控制。最后,采用计算机仿真技术对轮胎刚度系数确定与随机变化两种情况的车道线保持进行数字仿真分析,并对本文所提方法的正确性与有效性进行检验。
1 模型描述在不考虑路面倾斜的前提下,车辆横向运动模型可以采用横向位置误差与横摆角误差为基本状态变量描述如下[8, 9, 10]:
式中,ψr为横摆角误差;ys为横向位置误差;Iz为车辆的转动惯量;vx为车辆纵向速度;m为车辆质量;lf与lr分别为车辆质心到前、后轴的距离;Cf与Cr分别为车辆的前、后轮胎刚度;δ为车辆前后轮转角;ψd为期望横摆角;χ为车道中心线曲率,ψ·d=vxχ;a1=Cf+Cr;a2=Cflf-Crlr;a3=Cflf2+Crlr2。
参考文献[8],进一步深入考虑从转向机构到前轮转角δz的惯性延迟特性,引入一阶惯性环节来描述其动态特性为:
式中,u为系统输入;Te为惯性时间常数。为便于理解,定义横摆误差角速度ω与横向位置误差速度vy变量如下:
则上述模型可以改为如下形式:
车道线横向位置误差控制的任务是设计控制规律u=f(x),其中x为系统可测量的全部或部分状态,使得横向位置误差ys能在任意初始位置下渐进收敛到0。
考虑到车道线保持控制系统的物理特性,把上述系统模型(式(1))分为两部分,其中第1部分为式(4)、式(5),该部分中包含大量车辆动态系数,而且部分系数受路面摩擦、侧风等影响而难以确定,因此把该部分定义为不确定子系统;而第2部分则为式(2),该部分仅含惯性时间常数Te,该参数只和前轮转向的反应速度相关。而且一旦生产定型就比较固定,因此,把第2部分定义为相对确定的子系统。本文针对不确定子系统与确定子系统,分别采用滑模控制和反演控制的方法,并通过选取Lyapunov函数将其融合为一体。
2 反演滑模控制律设计不失一般性,定义横向位置误差ys的期望值为yrin,在无特殊说明情况下,yrin=0,定义误差变量ey=ys-yrin,则有:
考虑到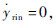 ,则有
,则有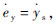 ,选取滑模面
,选取滑模面
式中C为滑模面参数。对其求导得:
代入式(3)得:
考虑到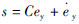 ,将式(5)代入式(9),则有:
,将式(5)代入式(9),则有:
设计δ的期望值为:
式中Ωa为带柔化函数的滑模控制项,可以设计为:
式中ka1,ka2,ε均为可调控制参数。
则有:
式中eδ=δ-δd,则有:
设计控制律
式中Ωb为带柔化函数的滑模控制项,其表达式为:
式中kb1与kb2为可调控制参数。
此时
选取Lyapunov能量函数如下:
求取能量函数的导数为:
选取ka1,ka2,kb1,kb2为正的常数,则:
根据Lyapunov稳定性理论,可以得到系统稳定,且s→0。
由于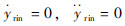 ,且选取C为正常数,则当s→0时,有ey=Ae-Ct(t为时间),则有ey→0,ys→yrin,即车道线横向位置误差能得以消除。
,且选取C为正常数,则当s→0时,有ey=Ae-Ct(t为时间),则有ey→0,ys→yrin,即车道线横向位置误差能得以消除。
在仿真分析中,车辆模型参数参照文献[11],假设车辆质量m为1 350 kg,转动惯量Iz为2 400 kg·m2,前轴距lf为1.46 m,后轴距lr为1.5 m,前、后轮胎的刚度Cf与Cr的标准值为65 kN/rad和75 kN/rad。 车辆纵向速度vx为25 m/s,转向延迟时间常数Te为0.05 s。上述模型参数目前在国内外广泛使用,是研究者普遍接受与认可的。车辆的初始横摆角误差为2°,初始横向位置误差为2 m,其他初始状态为0。
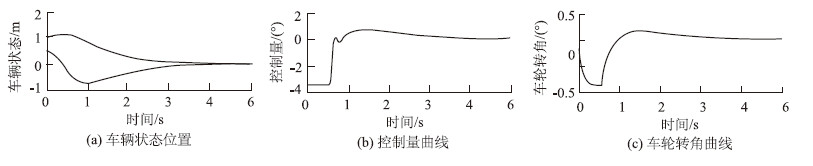
按照上文设计的控制规律,选取控制参数C=10,<ε=0.3,车辆被跟踪路径曲率半径为100 m,分别考虑前、后轮胎刚度Cf与Cr为标准值、[60, 70]和[70, 80]间的随机数。在两种滑模控制情况下进行数据仿真分析。图 1与图 2给出了文献[11]所示的传统滑模控制与自校正滑模控制效果图。

|
| 图 1 传统滑模控制效果图 Fig. 1 Control effect of traditional SMC |
|
| 图 2 自校正滑模控制效果图 Fig. 2 Effect of self-correcting SMC |
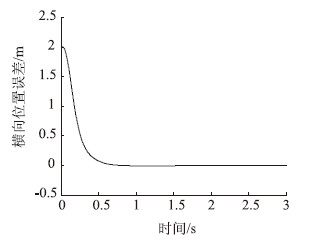
当轮胎的刚度Cf与Cr取值为标准值时,仿真结果如图 3~图 7所示
|
| 图 3 横向位置误差曲线 Fig. 3 Curve of lateral position error |

|
| 图 4 横向位置误差导数曲线 Fig. 4 Derivative curve of lateral position error |
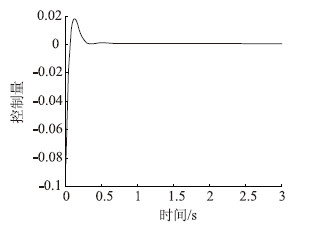
|
| 图 5 控制量曲线 Fig. 5 Curve of control quantity |
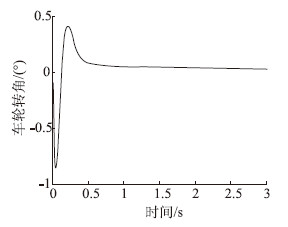
|
| 图 6 车前轮转向角曲线 Fig. 6 Curve of steering angle of front wheel |
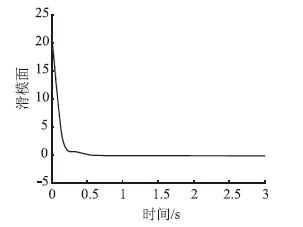
|
| 图 7 滑模面收敛曲线 Fig. 7 Converging curve of sliding mode surface |
通过对比可以看出,本文所设计的带柔化函数的反演滑模控制方案中,车辆的前轮转向角与控制量以及横向位置误差的导数均比较平滑,可以克服传统滑模方法在0~0.5 s内输出抖振较大,浪费能量且加快轮胎磨损的缺点,而且其横向位置误差能够在1 s内完全收敛到0,较自校正滑模控制具有更快的收敛速度。为了测试反演滑模控制的鲁棒性,并使仿真更接近实际情况,本文不同于其他文献的单次仿真分析,而采用严格的大量随机仿真分析来衡量控制算法的适应性,因此其结果比单次仿真更具有说服力。当然,不足之处在于对轮胎刚度之外的其他参数没有采用随机分析,但考虑到轮胎刚度是车辆模型中受外界环境影响最大的不确定参数,因此本文仿真也足以对未来的车辆真实试验提供理论指导与数据支持。
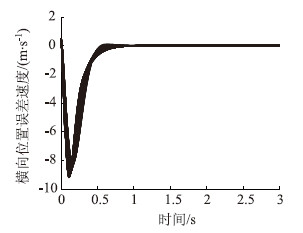
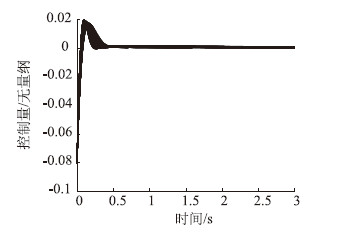
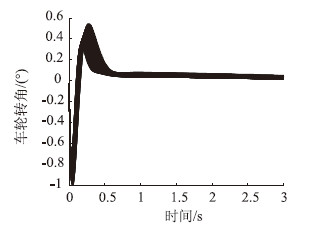
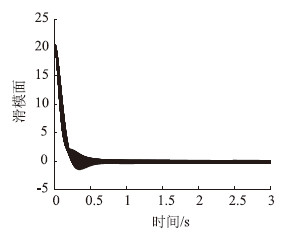
选取轮胎的刚度Cf与Cr取值为[60, 70]及 [70, 80]间的随机数,进行100次重复仿真,仿真结果如图 8~图 12所示。
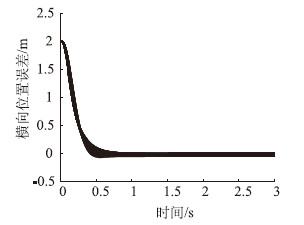
|
| 图 8 横向位置误差100次仿真收敛曲线 Fig. 8 One hundred simulation converging curves of lateral position error |
|
| 图 9 横向位置误差导数100次仿真收敛曲线 Fig. 9 One hundred simulation converging curves of derivative of lateral position error |
|
| 图 10 控制量100次仿真收敛曲线 Fig. 10 One hundred simulation converging curves of control quantity |
|
| 图 11 滑模面100次仿真收敛曲线 Fig. 11 One hundred simulation converging curves of sliding mode surface |
|
| 图 12 车前轮转向角100次仿真收敛曲线 Fig. 12 One hundred simulation converging curves of steering angle of front wheel |
以上100次随机仿真的结果表明,反演滑模控制算法在轮胎刚度区域给定区间随机变化时,具有很好的鲁棒性。从图 12可以看出,在模型参数随机变化的情况下,滑模面的收敛具有很好的一致性。控制算法的稳定性能够满足环境参数摄动的需求。从图 8可以看出,横向位置误差收敛的快速性也基本能够满足在1 s内收敛的需求。因此,基于柔化函数的反演滑模控制算法具有较好的鲁棒性,能够满足轮胎刚度参数不确定的需求。
4 结论本文针对车辆横向动力学简化线性模型,考虑前向轮自动转动系统的惯性延迟特性,设计了一类车道线横向误差的反演滑模复合控制器。 其中滑模控制对横向动力学模型不确定性的处理具有强鲁棒性优点;而反演控制对确定的转向系统具有层层倒推、环环相扣、精确巧妙的设计特点。最后,综合考虑了轮胎刚度系数随机不确定的复杂情况,进行了多次仿真,仿真结果进一步验证了本文方法的有效性。
车道线保持问题是一个复杂而又有意义的实际问题,本文将实际被控对象分解为确定与不确定两个子系统,其中不确定子系统包含车辆运动的复杂动态模型,难以精确建模,而且受地面路面、轮胎磨损等外界情况影响,因此针对该部分子系统采用强鲁棒性的滑模控制。而前轮转向系统模型仅含一个惯性时间常数,它与汽车设计参数相关,而且一旦生产定型,该参数是比较固定的。因此本文认为它是确定性较强的系统。针对该类确定性系统采用反演控制,无疑是最直接又有效的方法。
综上所述,本文把复杂系统按照物理实际情况分解为相对确定与不确定两部分,采用反演与滑模进行融合设计的思想,十分符合车辆自动驾驶中车道线保持问题的物理实际,同时对其他类似被控对象的设计也具有指导意义。最后,采用多次重复随机仿真的方法来验证本文控制算法的鲁棒性以及将确定子系统和不确定子系统分离设计的合理性,其仿真结果能够为未来车辆试验提供数据支持与理论参考。
| [1] | ZHANG Jing-ming, REN Dian-bo, CUI Sheng-min, et al. Direct Adaptive Control for Lane Keeping in Intelligent Vehicle Systems[J].Journal of Harbin Institute of Technology, 2009, 16(6):810-814. |
| [2] | ZHOU Jian-jun, ZHANG Man, WANG Mao-hua, et a1. Path Tracking for Agricultural Vehicle Based on Fuzzy Control[J].Transactions of the Chinese Society for Agricultural Machinery, 2009, 40 (4):151-156. |
| [3] | 张继业, 任殿波.具有不确定参数的车道保持终端滑模控制[J]. 大连海事大学学报, 2008, 34(3):81-84, 88. ZHANG Ji-ye, REN Dian-bo. Terminal Sliding Mode Control for Lane Keeping with Parametric Uncertainties[J]. Journal of Dalian Maritime University, 2008, 34(3):81-84, 88. |
| [4] | 金立生, 方文平, 候海晶.基于BP神经网络的车道保持控制系统[J].吉林大学学报:工学版, 2010, 40(3):650-654. JIN Li-sheng, FANG Wen-ping, HOU Hai-jing. Co-simulation of Lane Keeping Control System Based on BP Neural Network[J]. Journal of Jilin University: Engineering and Technology Edition, 2010, 40(3):650-654. |
| [5] | 王荣本, 马雷, 储江伟, 等.智能车辆转向变结构控制方法的研究[J].汽车工程, 2004, 26(1):1-4. WANG Rong-ben, MA Lei, CHU Jiang-wei, et al. A Research on Variable Structure Steering Control Method for Intelligent Vehicle[J]. Automotive Engineering, 2004, 26(1):1-4. |
| [6] | ZHAO S, LI Y, ZHENG L, et a1. Vehicle Lateral Stability Control Based on Sliding Mode Control[C]// Proceedings of the IEEE International Conference on Automation and Logistics. Jinan, China:IEEE, 2007:638-642. |
| [7] | AKAR M, KALKKUHL J. Lateral Dynamics Emulation Via a Four-wheel Steering Vehicle[J]. |
| [8] | LI Zhi-jun. Vehicle Merging Control for an Automated Highway System[D]. Blackburg, USA: Virginia Polytechnic Institute and State University, 1996. |
| [9] | 李玮, 王晶, 段建民. 车道线保持自校正滑模控制[J]. 公路交通科技, 2011, 28(6):136-140. LI Wei, WANG Jing, DUAN Jian-min. Self-tuning Sliding Mode Control for Vehicle's Lane Keeping[J]. Journal of Highway and Transportation Research and Development, 2011, 28(6):136-140. |
| [10] | 孙涵, 任明武, 唐振民, 等. 基于机器视觉的智能车辆导航综述[J].公路交通科技, 2005, 22(5):132-135. SUN Han, REN Ming-wu, TANG Zhen-min, et al. A Survey of Machine Vision Based Intelligent Vehicle Navigation[J]. Journal of Highway and Transportation Research and Development, 2005, 22(5):132-135. |
| [11] | 贾立山, 罗剑, 李世其. 基于车道线直线模型的道路曲率估计方法[J]. 江苏大学学报: 自然科学版, 2012, 3(4):152-157. JIA Li-shan, LUO Jian, LI Shi-qi. Road Curvature Estimation Based on Linear Lane Model[J]. Journal of Jiangsu University: Natural Science Edition, 2012, 3(4): 152-157. |
 2015, Vol. 32
2015, Vol. 32