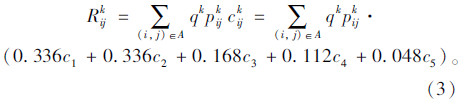扩展功能
文章信息
- 宋洋, 孙俊富
- SONG Yang, SUN Jun-fu
- 危险品道路运输网络风险-成本综合优化研究
- Study on Risk-cost Synthetic Optimization of Dangerous Goods Transport in Road Network
- 公路交通科技, 2015, Vol. 32 (10): 141-145,152
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 32 (10): 141-145,152
- 10.3969/j.issn.1002-0268.2015.10.023
-
文章历史
- 收稿日期: 2014-07-31
危险品的运输道路网络规划中,一方面,由于危险品的运输牵涉到较大规模的人身财产安全,因此通常受到政府管制,政府在规划其道路网络时,希望尽可能低降低运输过程中的风险,确保人身财产安全;另一方面,危险品运输企业往往倾向于在道路运输网络中选择运输成本最小的路径。因此,有必要进行危险品运输道路网络风险-成本综合优化研究,在政府目标和企业目标二者之间找到一个均衡点,从而保障危险品运输安全。
从国内外研究的发展历程来看,针对危险品运输的研究经过了以下3个阶段[1],即:危险品运输风险评价、危险品运输选线研究、危险品运输道路网络规划。
针对危险品风险的评价源于20世纪70年代。这一时期是起步阶段,多为框架性的建立,如定量的风险评价等。80年代时期,Chan和Saccomanno[2]在分析加拿大的事故数据之后得出以下结论:不同天气和不同时段的事故概率不同主要是由道路差异造成的。
20世纪90年代后,随着危险品风险评价发展迅速,研究从单纯的风险分析转向了风险、路径选择、设施选址等多方面。首开先河的是List等人[3],他们对80年代危险品运输风险评价和选线进行了综合分析。由于危险品的运输关系到风险和成本这一对矛盾的目标,而单一目标无法解决这种问题,因此多目标选线应运而生。Shobrys[4]和Robbins[5]以最小化吨位运输距离和最小化吨位影响人数作为选线标准,最早开展了多目标选线研究。
21世纪后,危险品运输又进入了另一个高度,即全局性的道路网络优化分析。Kara和Vert[6]首次提出了危险品运输网络设计的双层模型,政府关闭网络中的某些路段,减少暴露人口,从而使网络中的总风险最小。
本文从危险品道路运输的政府-企业双层规划特性出发,针对危险品运输道路网络规划上的风险和成本进行优化分析。首先对风险和成本进行了定量分析,建立了危险品运输道路风险-成本双层规划的数学模型和目标函数。并利用遗传算法对目标函数进行求解,借助Matlab程序获得运算结果和优化方案。
1 危险品道路运输风险-成本分析根据美国联邦公路管理局针对危险品运输时提出的建议,以下因素应该被考虑在内:人口密度、公路类型、危险品类型和运量、暴露风险和其他风险因素、历史事故、地形、对商业的影响、运输的成本等。在基于以上考虑,本文将危险品道路运输时需要考虑的因素归为以下7个方面,如图 1所示。

|
| 图 1 危险品道路运输考虑因素 Fig. 1 Considered factors for dangerous goods transport |
假设道路网络G(N,A),其中N表示节点的集合,A表示边的集合[7]。用(i,j)表示路段,则有i,j∈N,(i,j)∈A,lij表示路段长度 。假设每年有不同的k种危险品从各自的起点ok 运往各自的终点dk,其中 k∈{k1,k2,k3,…,K},运输量为qk;假设ok ~dk 路径由n个(i,j)路段组成,其中 n∈{1,2,3,…,N}。
1.1 危险品道路运输成本估算忽略其他成本因素,危险品道路运输的成本主要由运输量q和运输距离lij决定。设1个单位距离内1个单位运量的运输危险品k的成本为mk,运输总量为qk,则危险品k在路段(i,j)上的运输成本mijk=qkmklijk。那么ok ~ dk 路径的总成本mijk有:
1.2 危险品道路运输风险估算按照传统的风险定义,风险R等于事故发生概率P乘以事故后果的严重程度C
(1)路事故概率P分析
若用pijk则表示k类危险品在路段(i,j)上运输时发生事故的概率,且假设pijk在一个(i,j)路段上是不变的,则 。那么第k 类危险品在第n个(i,j)路段上发生事故的概率为:
。那么第k 类危险品在第n个(i,j)路段上发生事故的概率为:
(2)事故严重程度C分析
本文采用层次分析法(AHP)对以上影响危险品运输事故后果严重程度的5项指标进行量化分析,参考相关文献[8, 9, 10],并结合实际情况,得出以上5个因素的比较打分表格,如表 1所示。
| 影响因素 | c1 | c2 | c3 | c4 | c5 |
| c1 | 1 | 1 | 2 | 3 | 7 |
| c2 | 1 | 1 | 2 | 3 | 7 |
| c3 | 1/2 | 1/2 | 1 | 3/2 | 7/2 |
| c4 | 1/3 | 1/3 | 2/3 | 1 | 7/3 |
| c5 | 1/7 | 1/7 | 2/7 | 3/7 | 1 |
利用层次分析法定量分析得到影响危险品运输事故后果严重程度各个因素的权重为:0.285,0.285,0.142,0.095,0.041,0.095,0.057。综合事故概率分析和事故后果严重程度分析,用rijk表示危险品k在(i,j)路段上的风险,则 ok ~ dk路径上的风险rijk表示为:
1.3 危险品运输双层规划分析危险品运输道路网络双层规划的优化过程,如图 2所示,针对每一个风险水平r,在其对应的不同成本中搜寻出最低成本mmin,如在风险水平r1对应的成本 m11,m12,…,m1n 中搜寻出最低成本mmin1,r2对应一个最低成本 mmin2,rn 对应一个最低成本mminn,再在所有的最低成本mmin中搜寻出最小的值,即总最低成本mmin(反之亦然)。 同时,mmin对应的风险R既满足了政府的风险要求,也使企业获得了最低成本的风险值。

|
| 图 2 双层规划过程 Fig. 2 Bi-level programming process |
根据上述分析,可设上下层决策变量分别为:
上层:
下层:
则危险品道路运输网络双层规划模型可建立如下:
上层规划:
下层规划:
上述式中,式(4)和式(5)表示决策变量xijk和yij只能在1或0中取值;式(6)为政府的上层规划的风险函数,即政府希望在现有的道路网络中总运输风险最小;式(7)是上层约束条件,其意义是在现有的道路网络A中,若(i,j)路段允许运输危险品,则相反方向的(j,i)路段同样也允许;式(8)为企业的下层规划的成本函数,即企业期望在现有的道路网络中总运输成本最小;式(9)是下层约束条件,表示企业只能在政府规定的路径里选线。
3 遗传算法求解危险品运输风险-成本优化模型用遗传算法求解危险品运输路径优化问题的过程就是:将种群代入下层目标函数进行初步计算后,再将结果导入以上层目标函数转换而来的适应度函数,进行排序处理,再进行3个遗传操作:选择、交叉、变异[11, 12]。
3.1 参数设定根据本文计算的规模,设GEN为进化代数,最大进化数GENmax=20;GGAP为代沟,取1;XVOR为交叉概率,取值0.3;MUTR为变异概率,取值1/NVAR,NVAR为变量维度。
3.2 算法具体步骤本文采用了谢菲尔德大学(Sheffield University)开发的遗传算法工具箱GATOB对模型进行求解,步骤如下:
(1)初始种群的生成
本文个体为随机0-1矩阵,因此采用三维矩阵来生成具有若干个体的种群。
(2)下层目标函数计算
由于运输成本与运输路径成线性相关,因此本文采取dijkstra算法来计算最短路径,从而计算出每个个体对应的最低成本路径X。
(3)上层目标函数计算
转换后的上层目标函数即适应度函数,计算每个最短路径X对应的风险值。
(4)排序
采用遗传工具箱自带的ranking函数进行排序,其输出的结果为一列向量。
(5)选择、交叉、变异
利用遗传算法工具箱自带select、recombin和mut函数完成选择、交叉和变异。
4 实例分析本文选取了天津市两交易市场之间的危险品运输作为实例进行分析。2个交易市分别为天津危险化学品交易市场,位于天津市内环线金狮立交桥旁;和滨海新区大港分市场,位于天津市滨海新区大港交通主干道世纪大道86号。
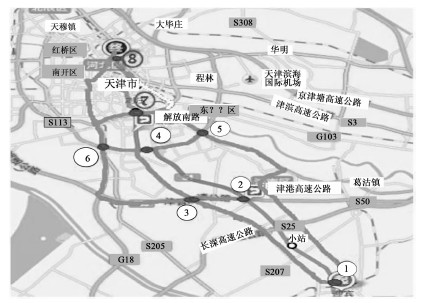
在分析位置、地形等实际情况后,初步选定运输网络包括如图 3所示的几条路线,其中共有8个节点。
|
| 图 3 天津市危险品道路运输网络图 Fig. 3 Dangerous goods transport road network in Tianjin |
根据上述分析,对各项指标按一定标准进行评价打分,得到邻接矩阵如下。
运输距离:
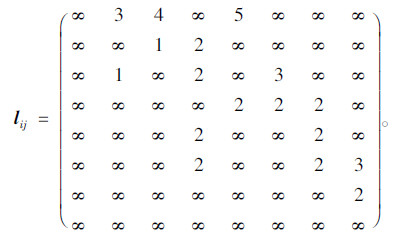
道路事故概率:

道路上人口暴露:

道路附近人口暴露:

财产损失:

环境污染:

应急响应效率:

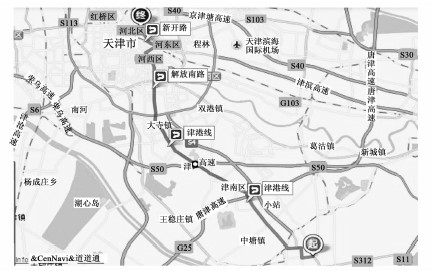
设种群大小NIND=8,变量维度NVAR=64。将实例信息转化为Matlab语句代入程序中进行计算,调用MATLAB遗传算法工具箱GATOB模块,对程序做适当调整,将遗传算法进行适当改良,提高全局搜索能力,计算出的最优路径为:1—3—4—7—8。实际路径如图 4所示:从滨海新区危险品交易市场①出发,沿津港线卫津路经过节点③进入S107道,随后经过节点④进入解放南路,到达节点⑦,再沿新开路到达终点⑧天津市危险化学品交易市场。
|
| 图 4 天津市危险品道路运输最优路径图 Fig. 4 Optimal path for dangerous goods road transport in Tianjin |
此路径的风险与成本同最短路径的比较如表 2所示。
| 最优路径 | 路径 | 1—3 | 3—4 | 4—7 | 7—8 | 总计 |
| 风险 | 1.16 | 1 | 4.52 | 8.994 | 15.624 | |
| 成本 | 4 | 2 | 2 | 2 | 10 | |
| 最短路径 | 路径 | 1—2 | 2—4 | 4—7 | 7—8 | 总计 |
| 风险 | 1.048 | 4.26 | 4.52 | 8.994 | 18.772 | |
| 成本 | 3 | 2 | 2 | 2 | 9 |
通过对比,最短路径由于成本值最低,是企业追求最低成本的最佳选择,但该路径风险值却偏高,为4.26;而最优路径虽然在选择3—4路段时,使得成本值略有增加,但风险值却大大降低,符合管理者追求低风险的目标。因此本实例求解出的1—3—4—7—8路径符合双层模型需求,同时满足了管理者低风险与企业低成本的要求,为最佳路径。
5 结论本文针对危险品运输的双层特性,将成本和风险两个互相冲突的问题利用双层规划进行了建模。并且相对全面地考虑了事故后果的影响因素,将危险品事故中的人口暴露细分为道路上人口和道路附近人口,将应急救援能力对危险品事故的缓解作用加入了评价指标。根据实际情况对指标进行打分评价,确定了较为合理的权重。利用遗传算法对危险品运输网络双层模型的求解,使最优解同时满足对风险和成本控制的需求。
| [1] | 任常兴. 基于风险分析的危险品道路运输路径优化方法研究[D].天津:南开大学, 2007. REN Chang-xing. Study on Transport Routing Optimal Method for Dangerous Goods Based on Risk Analysis[D].Tianjin: Nankai University, 2007. |
| [2] | SACCOMANNO F F, CHAN A Y W. Economic Evaluation of Routing Strategies for Hazardous Road Shipments[J]. Transportation Research Record, 1985, 1020:12-18. |
| [3] | LIST G F, MIRCHANDANI P B, TURNQUIST M A, et al. Modeling and Analysis for Hazardous Materials Transportation: Risk Analysis, Routing/Scheduling and Facility Location[J]. |
| [4] | SHOBRYS D. A Model for the Selection of Shipping Routes and Storage Locations for a Hazardous Substance[D]. Baltimore: Johns Hopkins University, 1981. |
| [5] | ROBBINS J. Routing Hazardous Materials Shipments[D]. Bloomington: Indiana University, 1981. |
| [6] | KARA B Y, VERTER V. Designing a Road Network for Hazardous Materials Transportation[J]. |
| [7] | 储庆中, 张家应, 谢之权. 基于双层规划的危险品道路运输网络设计[J].重庆交通大学学报:自然科学版, 2010, 29(4):597-603. CHU Qing-zhong, ZHANG Jia-ying, XIE Zhi-quan. Road Network Design for Hazardous Materials Transportation Based on Bi-level Programming[J]. Journal of Chongqing Jiaotong University:Natural Science Edition, 2010, 29(4): 597-603. |
| [8] | 宋伟程, 帅斌, 陈钢铁. 基于点危险源的危险品运输路径优化研究[J] .中国安全科学学报, 2012, 22(2):116-121. SONG Wei-cheng, SHUAI Bin, CHEN Gang-tie. Dangerous Goods Transport Path Optimization Based on Point of Hazard[J]. China Safety Science Journal, 2012, 22(2):116-121. |
| [9] | 吴锋, 王晓艳. 基于模糊Petri 网的危险品运输安全评估模型及应用[J]. 中国安全科学学报, 2011, 21(1):93 - 98. WU Feng, WANG Xiao-yan. A Safety Evaluation Model for Dangerous Goods Transportation Based on Fuzzy Petri Nets and Its Application[J]. China Safety Science Journal, 2011, 21(1): 93-98. |
| [10] | 马昌喜, 广晓平, 吴芳, 等. 发达运输网络环境下危险品公路运输路径决策[J].交通运输系统工程与信息, 2009, 9(4):134-139.Hazardous Material in Developed Transportation Network[J].Journal of Transportation Systems Engineering and Information Technology, 2009, 9(4):134-139. |
| [11] | 宋洋, 徐桢, 王燕青. 基于蚂蚁算法的危险品运输路径优化研究[J].安全与环境工程, 2014, 21(1):148-152. SONG Yang, XU Zhen, WANG Yan-qing. Route Optimization for Dangerous Goods Transportation Based on Ant Colony Algorithm[J].Safety and Environmental Engineering, 2014, 21(1):148-152. |
| [12] | 冯树民, 殷国强 . 规划层面的危险品运输路径优化模型[J] .哈尔滨工业大学学报, 2012, 44(8):53-56. FENG Shu-min, YIN Guo-qiang. Transport Route Optimization Model of Dangerous Goods at the Planning Level[J]. Journal of Harbin Institute of Technology, 2012, 44(8):53-56. |
 2015, Vol. 32
2015, Vol. 32