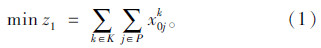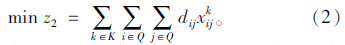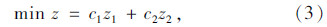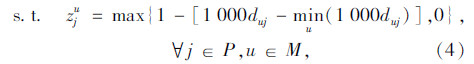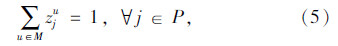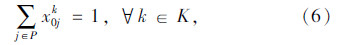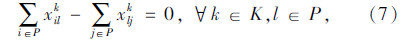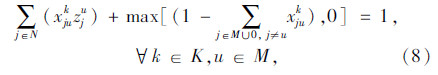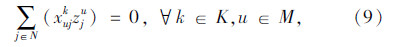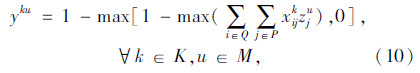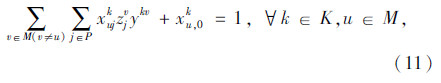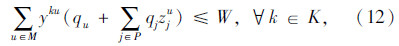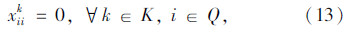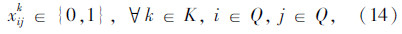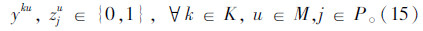2015, Vol. 32扩展功能
文章信息
- 覃运梅, 毛海军, 黑秀玲
- QIN Yun-mei, MAO Hai-jun, HEI Xiu-ling
- 基于自动快递机的快递配送车辆路径优化研究
- Optimizing of Vehicle Routing for Express Delivery Based on Automatic Parcel Machine
- 公路交通科技, 2015, Vol. 32 (10): 134-140
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 32 (10): 134-140
- 10.3969/j.issn.1002-0268.2015.10.022
-
文章历史
- 收稿日期: 2014-08-15
2. 广西科技大学 汽车与交通学院, 广西 柳州 545006
2. School of Automobile and Transportation, Guangxi University of Science and Technology, Liuzhou Guangxi 545006, China
快递需求量的增长对当前的快递派送模式提出了新的挑战。国家邮政局的数据表明，近3年我国的快递业务量年均增长率在50%以上，快递量的急剧增长对快递业的服务能力提出了更高的要求；而消费者的有效申诉年均增长1倍以上，远高于快递量的增长速度，且申诉类别集中在延误和投递服务方面，表明快递业的服务水平远跟不上快递量的增长需求。研究新的快递派送模式，提高快递配送效率和服务水平成了迫在眉睫的课题。
传统的快递派送模式是由快递员把快件送至其所负责区域的客户家门口并通知客户取件，若客户不在则需进行二次派送。经研究发现，造成快递服务效率不理想的主要原因是交接快件的时间和地点的对接约束以及配送模式的缺陷，若能够固定快递的交接地点而分离交接时间，并优化配送路线方案，则可以使快递配送的服务效率得到实质性的提高。因此，本文提出了基于自动快递机(简称快递机)的快递派送模式，通过在快递客户需求点附近布设自动快递机，当客户同意把快件放到快递机时，快递员把快件送到快递机后离开，客户收到信息通知后自主安排时间到快递机自助提取快件。利用快递机取件解决了客户取件时必须与快递员在时间和地点达到一致的问题，减少了交接快件的时间及其带来的麻烦，有效提高快递服务效率和服务水平，同时降低成本、节约资源。
目前，相关学者对物流快递有了一定的研究。文献[1]研究了基于随机时间和需求的快递路线和调度安排的方案制订和实时调整的模型，并设计启发式算法求解。文献[2]研究了城市快递路径和调度问题，构造带硬时间窗的多目标模型，提出了一种多目标分散搜索框架。文献[3]建立了规划模型和实时调整模型来解决快递公司面临不确定需求进行的快递路线和日程安排问题。文献[4] 研究一种随机车辆路径问题，建立机会约束规划模型和随机规划模型，并设计了基于禁忌搜索的启发式算法来求解模型。文献[5]分析了基于网络中值问题的设施选址问题。文献[6]分析了有时间窗的快递动态取、送件问题的等候策略问题，定义并比较了4种策略。文献[7]考虑地理约束和偏好行为建立了快递网络模型。文献[8]提出了两阶段混合算法来解决带时间窗取、送货的多车辆路径问题，第一阶段用一个简单的模拟退火算法来减少线路的数量;第二阶段使用大型邻域搜索来减少行驶总成本。文献[9]用蚁群算法来解决同时取、送货的车辆路径问题，提出了使用构造规则以及2个多路径局部搜索方案，该算法也可以解决回程的车辆路径问题和混合负载问题。文献[10]提出优化整合正向配送和反向收集物流服务，并开发有效的启发式算法来解决这个问题。文献[11, 12, 13, 14]对物流配送网络及调度优化进行了较深入的研究。
以上文献是对配送网络及路径的优化及相关优化算法的研究，但这些文献都没有考虑到目前随着电子商务快速发展而带来的快递物流的多元化发展问题，尤其是当前自动快递机已经尝试性地出现在一些大城市的物流快递的配送业务中，而相关的应用模式及其理论方法仍未有系统的研究。本文在相关优化研究的基础上，把快递派送的系统优化问题表述为多目标模型，采用带启发式知识的元胞遗传算法对模型进行求解，对快递配送车辆的路径进行优化。
1 数学模型 1.1 问题描述考虑传统快递配送模式与人们的收件习惯，基于快递机的快件配送要与传统模式有效融合。在寄件人寄件时、或者电子商务模式下客户在下订单时选择“送件上门”、或者“送件到快递机”2种模式之一。若选择了“送件到快递机”模式，则在送件时直接把该快件送到客户指定的快递机地址(当客户不指定快递机时，由系统直接分派到最近的快递机)。若客户选择“送件上门”或者不做选择时，则按照传统模式送件上门，当送件到门时客户不在的时候，经与客户协商同意则把快件送到最近的快递机，否则进行重新派送。
基于快递机的快件配送与传统配送不一样，在送件的过程中，有可能原来要求送件上门的客户临时情况有变而需要改为送到最近的快递机。因此在送件线路的制订时，对于归属于同一个快递机的所有客户，应该先到达需要送件上门的客户点，最后再到达快递机，以便把签收失败的快件经过客户同意后放进所属的快递机，然后再进入下一个快递机所服务的客户。
1.2 问题假设(1)物流公司派件的车型统一，车辆来源足够。
(2)同一个快递机及其所属客户点的所有快件由同一辆车派送，不拆分给不同车辆。
(3)派件车辆从快递公司配送中心依次送件到客户需求点和快递机，完成运输任务后返回原地。
1.3 模型建立 设M={1,2,…,M}为配送范围的快递机集合；N={M+1,M+2,…,M+N}为需要送件上门的客户点集合；P=M∪N={1,2,…,M,M+1,…,M+N}为所有待送件的快递机和客户点的集合；O={0}为配送中心；Q=O∪M∪N={0,1,2,…,M,M+1,…,M+N}为配送中心、所有待送件的快递机和客户点的集合；K={1,2,…,K}为配送车辆的集合；dij为从i到j的运输距离；W为车辆的装载能力；qj为j点(含快递机和客户点)待配送的快递量。
执行配送任务的车辆数最少的目标：
配送车辆总的行驶里程最小的目标：
设派出一辆车的固定使用成本为c1，单位距离运输费率为c2，转化为单一目标，建立模型如下：
式中,z1为执行配送任务的车辆数;z2为配送车辆总的行驶里程;z为将配送车辆的固定使用成本和车辆行驶的运费转化得到的总成本。
模型中，式(3)表示所有车辆的总费用最小的目标；式(4)表示客户点归属于最近的快递机，取整精度为“m”，当j=u时zuu=1表示快递机归属于它本身；式(5)表示同一个客户只归属于一个快递机；式(6)表示车辆均从快递公司配送中心出发；式(7)表示车辆行驶线路的连贯性；式(8)表示车辆服务完快递机u所属的其他客户点后最后驶入快递机u，若快递机u没有其他所属的客户点需要送件上门时，则直接从上一个快递机或配送中心直达快递机u；式(9)表示车辆到达快递机u后，不再返回该快递机所属的其他客户点；式(10)中当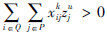
时，得到yku=1，表示车辆k为快递机u及归属于快递机u的客户点服务；式(11)表示车辆服务快递机u后驶入下一个快递机v所属的客户点j(包含快递机v及其所属的其他客户点)或者回到配送中心；式(12)表示车辆配送总量不超过车辆的装载能力；式(13)~式(15)表示变量的取值范围。本模型与一般车辆路径问题的最大不同之处是限定了快递机及其所属客户点之间的行驶次序。
同时为快递机和需要送件上门的客户送件问题是NP难题，随着快递机数量和客户点数量的增加，问题的求解难度加大，求解时间将呈指数增加。遗传算法(GA)是求解这类难题比较有效的方法，但它同时存在容易“早熟”收敛以及求解速度不够快的问题[13]。针对解的特点，本文采用元胞遗传算法(Cellular Genetic Algorithm,CGA)[14, 15]对问题进行求解，算法将元胞自动机作用机理和遗传算法进行有机结合，将单个的元胞视为种群中的个体，将种群中的个体按照一定的拓扑结构分布，借助元胞自动机模型中的邻居结构实现遗传算法的操作。
2.1 元胞邻域结构及种群分布一般的遗传算法中，种群中的个体以离散形式分布；而在元胞遗传算法中，种群中的个体按照一定的拓扑结构分布。本文采用最为常用的Moore型邻域结构[14]，每个中心元胞有8个邻居元胞，每个个体仅与邻居个体之间进行遗传操作，有效降低了算法的选择压力，提高搜索效率。种群分布如图 1所示。
|
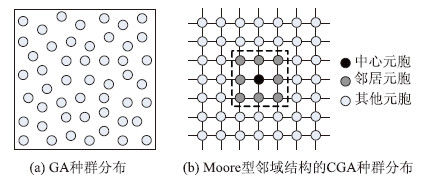
| 图 1 种群分布示意图 Fig. 1 Schematic diagram of population distribution |
采用十进制编码方法。一个可行解可编成长度为K+M+N+ 1的个体，根据问题的假设条件，K最大可能值为M，故编码长度也可表示为2M+N+1。编码取值范围为[0,M+N]且为整数，其中，“0”为快递配送中心;[1,M]为快递机编号;[M+1,M+N]为需要送件上门的客户点的编号。一个染色体中两个相邻的“0”之间的数列就是车辆依次为客户及快递机送件的行驶路线，染色体编码串(0,4,9,1,7,5,2,0,6,8,10,3,0,0)对应的解码为：x0,41，x4,91，x9,11，x1,71，x7,51，x5,21，x2,01，x0,62，x6,82，x8,102，x10,32，x3,02的取值为“1”，其他为“0”。
2.3 适应度函数由于模型的目标函数是最小化问题，且问题的特性决定了目标函数值为正值，故适应度函数可以采用目标函数值z的倒数，设第j个染色体对应的目标函数值为 z(j)，则适应度可以表达为 fj=1/z(j)。 当染色体不满足所有约束条件时，令适应度函数值为一个极小值。适应度函数值越大，表示方案的总费用越小，该染色体个体被遗传到下一代的概率就越大。
2.4 基于启发知识的初始种群产生根据配送过程先到达需要送件上门的客户点，再到达客户所属的快递机的特性，构造基于启发式知识产生初始群体个体的方法为：根据zju划分客户点归属于对应的快递机，将每个快递机及其所属的客户点视为分派车辆的一个“单元”。设置M+1个“0”，以单元1为开始，加上最近的其他单元的快件量，依次累加直到超出车辆运载能力，则把最后考虑的单元作为第2辆车的开始任务，之前的单元作为车辆1的运输任务，对于车辆1所负责的各个单元，先排列快递机所属的客户编号，再到快递机编号，此时得到第1个染色体个体；再分别以单元2，单元3，…，单元M为开始获得第2个，第3个，…，第M个染色体。若M≥R，则取前R个染色体作为初始种群；若M＜R，则按照下述方法继续寻找新的染色体：保持染色体中“0”以及表示快递机编号的1~M的数字的位置不变，任取一个单元内表示客户点位置的编号顺序进行随机更改，则获得一个新的染色体，直至得到R个染色体，初始群体产生。按照这个方法得到的初始群体保证了解的可行性，且适应度值较高。
2.5 算法实现过程(1)算法初始化，进行染色体编码，设置群体规模R、遗传操作的交叉概率Pc、变异概率Pm以及最大重复选择次数Tmax，算法最大迭代次数T，初始化过程包括：
①用基于启发知识的方法产生包括R个染色体的初始群体。
②计算初始群体中各个染色体的适应度值，选择适应度值最高的个体作为历史最佳个体。
(2)重复以下遗传操作，直到满足算法终止条件。
① 选择操作
本文将基于排名的选择方法和轮盘赌选择法进行综合改进，以解决基于排名的选择方法有可能导致局部收敛的问题和轮盘赌选择法误差较大有可能导致适应度较高的个体也未被选上的问题。具体方法如下：
(a)令当前染色体i被选择进入下一代的次数为ti=0，将当前染色体按照适应度函数值从高到低取前(1/3)R个直接选择被选择进入下一代的操作，并令被选择的染色体i对应的值ti=ti+1，还有(2/3)R个个体将从当前染色体中按照改进的轮盘赌选择法进行选择。
(b) 令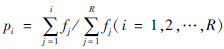 
。
(c)设群体中同一个染色体被重复选择的最大次数为Tmax，产生随机数ξ∈[0, 1]，若pi－1<ξ≤pi，且ti<Tmax，则染色体i被选择进入下一代，令ti=ti+1；否则若ti≥Tmax，染色体i不能再选择，避免同一个染色体被过多次重复选择。重复本步骤，直至得到R个染色体。
②交叉操作
在种群个体构成的二维空间矩阵中，对选定的一个中心元胞作为交叉操作的父代之一，再在邻居结构中选择适应度值最高的一个邻居元胞作为父代之二，对配对好的染色体进行二次交叉，将一般遗传算法中的交叉概率Pc表示两部分，先以Pc/2的概率以“单元”为最小单位进行交叉，再以Pc/2的概率在“单元”内部进行交叉。若交叉产生的新个体优于中心元胞，则用新个体替换中心元胞，否则，不替换。交叉操作如图 2所示。
|
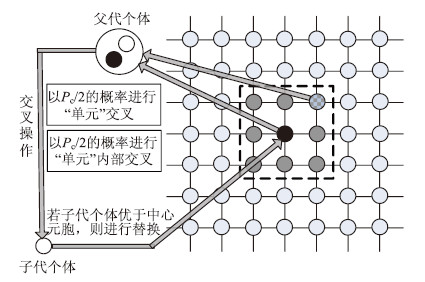
| 图 2 用元胞遗传算法进行二次交叉操作 Fig. 2 Two-step crossover operation by CGA |
依次考虑所有的中心元胞。对交叉得到的新个体，判断是否符合约束条件，如不符合，则令其适应度值为一个极小值，以降低该个体被遗传到下一代的概率。
③变异操作
通过变异操作增加种群的多样性。采用位置插入式变异，即随机选定个体中某一个点的基因插入串中的另一个随机位置上。将变异概率Pm分成两部分依次考虑各个染色体，产生随机数ξ∈[0,1]，若ξ≤Pm/2，则以“单元”为最小单位进行变异;若Pm/2<ξ≤Pm，则在“单元”内部进行变异;若ξ>Pm，则该对染色体不进行变异操作。同样，在变异的过程中若个体不满足所有约束条件，令其适应度值为一个极小值。
④ 对本次遗传操作得到的群体计算适应度值，若群体中的最优适应度值大于历史最优适应度值，则用当前群体的最优适应度值及其对应的个体对历史最优值进行更新，否则不更新。
⑤判断是否达到算法终止条件：(a)算法迭代到最大迭代次数T；(b)有连续Tsame代的最佳染色体相。若满足终止条件，迭代搜索过程结束，输出首次出现历史最优值的迭代位置，最优适应度值以及最佳个体，否则返回步骤①继续迭代优化。
(3)运行算法若干次，比较选取最优解，得到快递配送车辆送件路径的优化方案。
3 算例 3.1 基本数据假设某快递企业对一配送区域内的快件进行配送，各个快递机及客户需求点的坐标值及待配送的快件量如表 1所示，其中1~10编号为快递机，其他点为客户需求点，配送中心的坐标为(0,0)，车辆装载能力W=250 件。
| 序号 | x/km | y/km | qi/件 | 序号 | x/km | y/km | qi/件 | |
| 1 | 0.6 | 1.2 | 50 | 31 | 1.3 | -1.3 | 5 | |
| 2 | 1.5 | 0.8 | 40 | 32 | 1.8 | -0.5 | 7 | |
| 3 | 0.6 | -0.8 | 60 | 33 | -0.4 | -0.9 | 8 | |
| 4 | 1.2 | -0.2 | 70 | 34 | -0.5 | -1.6 | 2 | |
| 5 | 1.7 | -1.5 | 80 | 35 | -0.8 | -0.2 | 6 | |
| 6 | -0.6 | -1.3 | 55 | 36 | -0.9 | -1 | 3 | |
| 7 | -1.5 | -0.8 | 80 | 37 | -1 | -0.5 | 4 | |
| 8 | -0.4 | 0.8 | 90 | 38 | -1.2 | -1.3 | 5 | |
| 9 | -0.9 | 0.4 | 50 | 39 | -0.5 | -1.1 | 6 | |
| 10 | -1.5 | 1 | 60 | 40 | -0.6 | -0.8 | 3 | |
| 11 | 0.4 | 0.6 | 3 | 41 | -1.6 | -0.6 | 8 | |
| 12 | 1.4 | 0.2 | 4 | 42 | -1.7 | -1.5 | 4 | |
| 13 | 0.7 | 1.8 | 5 | 43 | -1.7 | -1.3 | 2 | |
| 14 | 0.7 | 0.9 | 2 | 44 | -1.8 | -0.5 | 3 | |
| 15 | 1 | 1.5 | 5 | 45 | -1.9 | -0.8 | 6 | |
| 16 | 1.1 | 0.7 | 7 | 46 | -0.5 | 0.1 | 5 | |
| 17 | 1.2 | 1 | 6 | 47 | -0.7 | 0.9 | 4 | |
| 18 | 1.3 | 0.8 | 8 | 48 | -0.6 | 0.5 | 8 | |
| 19 | 1.5 | 1.6 | 4 | 49 | -0.9 | 0.8 | 2 | |
| 20 | 1.8 | 1.2 | 3 | 50 | -0.7 | 1.2 | 6 | |
| 21 | 0.3 | -0.8 | 5 | 51 | -0.3 | 0.9 | 3 | |
| 22 | 0.5 | -1.1 | 6 | 52 | -1.2 | 1.5 | 7 | |
| 23 | 0.7 | -0.9 | 2 | 53 | -1.7 | 0.7 | 6 | |
| 24 | 0.9 | -1.4 | 6 | 54 | -0.4 | 1.4 | 1 | |
| 25 | 1 | -1.5 | 4 | 55 | -0.6 | 1 | 6 | |
| 26 | 1.2 | -0.7 | 8 | 56 | -1.6 | 0.6 | 3 | |
| 27 | 1.5 | -1.7 | 3 | 57 | -1.3 | 0.2 | 4 | |
| 28 | 1.6 | -0.6 | 6 | 58 | -1.8 | 1.5 | 8 | |
| 29 | 1.9 | -1.6 | 4 | 59 | -1.9 | 1.6 | 2 | |
| 30 | 1 | -1 | 6 | 60 | -1.9 | 1 | 5 |
本例中配送单元由50个客户需求点、10个快递机和1个配送中心组成，设车辆固定使用成本c1=80元，可变成本c2=5元，种群大小R=49，交叉概率Pc=0.8，变异概率Pm=0.1，迭代终止代数T=500，最大相同最佳染色体代数Tsame=50，染色体最大重复选择次数Tmax=5。
3.2 结果及分析应用CGA算法，用计算机进行编程运算。通过算法运行计算，第23次运行第39次迭代得到的最优解适应度值为f=1.983×10－3，共需要4辆车执行配送任务，目标函数即总成本为z=504.241元，最优解如表 2所示。
| 配送车辆 | 决策变量yku | 决策变量xijk | 行车路径 |
| Vehicle 1 | y1,3,y1,4, y1,2=1 |
x0,211,x21,221,x22,241,x24,301,x30,231,x23,31,x3,261, x26,281,x28,321,x32,121,x12,41,x4,161,x16,171,x17,191, x19,201,x20,181,x18,21,x2，01=1 |
0—21—22—24—30—23—3—26—28—32— 12—4—16—17—19—20—18—2—0 |
| Vehicle 2 | y2,1,y2,8, y2,9=1 |
x0,112,x11,142,x14,152,x15,132,x13,12,x1,542,x54,502,x50,552, x55,472,x47,512,x51,82,x8,482,x48,462,x46,352, x35,572,x57,492,x49,92,x9,02=1 |
0—11—14—15—13—1—54—50—55—47 —51—8—48—46—35—57—49—9—0 |
| Vehicle 3 | y3,7,y3,10=1 |
x0,373,x37,383,x38,423,x42,433,x43,453,x45,443,x44,413, x41,73,x7,563,x56,533,x53,603,x60,583,x58,593,x59,523, x52,103,x10,03=1 |
0—37—38—42—43—45—44—41—7—56 —53—60—58—59—52—10—0 |
| Vehicle 4 | y4,6,y4,5=1 |
x0,334,x33,404,x40,364,x36,394,x39,344,x34,64,x6,254, x25,314,x31,274,x27,294,x29,54,x5,04=1 |
0—33—40—36—39—34—6—25—31—27 —29—5—0 |
| 备注 | 其余为0 | 其余为0 | — |
为了进一步验证本文带启发知识的元胞遗传算法(CGA)的有效性，针对本例提供的数据，采用普通遗传算法(GA)进行对比运算，两种算法的基本参数设置相同，两种算法各随机运算100次，每次运行最大迭代次数为500代。表 3给出了用两种算法分别进行寻优运算100次得到的对比结果。
| 算法 | 平均最优值 | 历史最优值 | 出现最优解 的平均迭代 次数 | ||
| 适应度值/ (×10-3) | 目标函数 值/元 | 适应度值/ (×10-3) | 目标函数 值/元 | ||
| GA | 1.866 | 536.075 | 1.954 | 511.844 | 66 |
| CGA | 1.964 | 509.234 | 1.983 | 504.241 | 12 |
从各自100次的运行结果中，分别选取最优解进行对比，图 3给出了两种算法求得的最优方案行车路径的示意图，图中每一个回路表示一辆车的运行路线。图 4给出了两种算法求得的最优方案的收敛趋势。
|
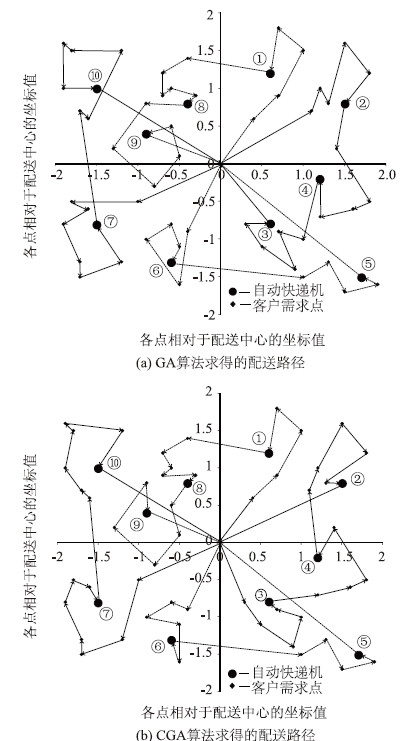
| 图 3 两种算法求得的最优解路径(单位：km) Fig. 3 Optimal routing schemes solved by 2 algorithms(unit：km) |
|
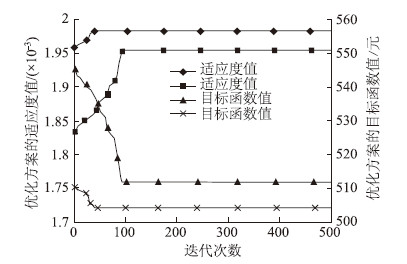
| 图 4 两种算法求得的最优解收敛趋势对比图 Fig. 4 Comparison of convergence trends of optimal solutions solved by 2 algorithms |
由图 2可看出，CGA算法能够更快地收敛于最优解。从表 3中看出，通过100次随机计算，CGA算法平均12次迭代就能获得最优解，而GA算法要多迭代40多代才能得到最优解，而且CGA算法得到的平均最优值优于GA算法5%左右，历史最优值优于GA算法的1.5%。计算结果表明，CGA算法的寻优性能优于GA算法，优化结果更好，收敛速度也更快。
4 结论本文在分析基于自动快递机的快递送件作业特点的基础上，建立了快递送件车辆分派任务及其行车路线的数学模型，模型突出了快递机及其所属客户点之间的行驶次序，并设计了基于模型特点的带启发式知识的元胞遗传算法。通过实例仿真验算了模型和算法的有效性，特别是问题规模较大时算法具有较强的寻优能力，为解决较大规模的快递送件问题提供了有效的决策途径。
| [1] | YAN S Y, LIN J R, LAI C W. The Planning and Real-time Adjustment of Courier Routing and Scheduling Under Stochastic Travel Times and Demands[J]. Transportation Research Part E: Logistics and Transportation Review, 2013, 53(7):34-48. |
| [2] | CHANG T S, YEN H M. City-courier Routing and Scheduling Problems[J]. |
| [3] | GORDON F H, LAI C W, HAMILTON M I. International Express Courier Routing and Scheduling Under Uncertain Demands[J]. |
| [4] | LI X, TIAN P, LEUNG S C H. Vehicle Routing Problems with Time Windows and Stochastic Travel and Service Times: Models and Algorithm[J]. |
| [5] | BERMAN O, KRASS D, MENEZES M B C. Facility Reliability Issues in Network P-median Problems Strategic Centralization and Co-location Effects[J]. |
| [6] | MITROVIC-MINIC S, LAPORTE G. Waiting Strategies for The Dynamic Pickup and Delivery Problem with Time Windows[J]. |
| [7] | YANG H, NIE Y, ZHANG H, et al. Insight to The Express Transport Network[J]. |
| [8] | BENT R, HENTENRYCK P V. A Two-stage Hybrid Algorithm for Pickup and Delivery Vehicle Routing Problems with Time Windows[J]. |
| [9] | GAJPAL Y, ABAD P. An Ant Colony System (ACS) for Vehicle Routing Problem with Simultaneous Delivery and Pickup[J]. |
| [10] | CHANG T S, LIAO Y F. Routing Strategies for Integrating Forward Distribution and Reverse Collection[J]. |
| [11] | 温惠英, 孙博. 基于离散粒子群算法的协同车辆路径问题[J]. 公路交通科技, 2011, 28(1):149-153, 158. WEN Hui-ying, SUN Bo. Resolving Collaborative Vehicle Route Problem Based on Discrete Particle Swarm Optimization[J]. Journal of Highway and Transportation Research and Development, 2011, 28(1): 149-153, 158. |
| [12] | 赵佳虹. 时变条件下应急物流多目标LRP研究[J]. 公路交通科技, 2012, 29(4):137-142, 148. ZHAO Jia-hong. Multi-objective Location-routing Problem in Emergency Logistics as Time Varies[J]. Journal of Highway and Transportation Research and Development, 2012, 29(4):137-142, 148. |
| [13] | 王雅琳, 李开峰, 马杰, 等. 遗传算法在企业铁路取送调车作业优化中的应用[J].系统工程, 2007, 25(3): 94-99. WANG Ya-lin, LI Kai-feng, MA Jie, et al. Application of Genetic Algorithm to Optimal Operation for Placing-in and Taking-out of Wagons at Enterprise Railway[J]. Systems Engineering, 2007, 25(3): 94-99. |
| [14] | 朱大林, 詹腾, 张屹, 等. 基于元胞小生境遗传算法的物流配送路径优化[J]. 组合机床与自动化加工技术, 2013(1):121-125. ZHU Da-lin, ZHAN Teng, ZHANG Yi, et al. Logistics Distribution Route Optimization Based on Cellular Niche Genetic Algorithm[J].Modular Machine Tool & Automatic Manufacturing Technique, 2013(1):121-125. |
| [15] | 陈昊, 黎明, 江泽涛, 等. 处理动态优化问题的演化元胞遗传算法[J]. 系统工程与电子技术, 2013, 35(5):1115-1121. CHEN Hao, LI Ming, JIANG Ze-tao, et al. Evolution Cellular Genetic Algorithm for Solving Dynamic Optimization Problem[J]. Systems Engineering and Electronics, 2013, 35(5):1115-1121. |