扩展功能
文章信息
- 杨春霞, 符义琴, 鲍铁男
- YANG Chun-xia, FU Yi-qin, BAO Tie-nan
- 基于相似性的短时交通流预测
- Short-term Traffic Flow Prediction Based on Similarity
- 公路交通科技, 2015, Vol. 32 (10): 124-128
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (10): 124-128
- 10.3969/j.issn.1002-0268.2015.10.020
-
文章历史
- 收稿日期: 2014-10-24
短时交通流预测是道路交通控制、诱导系统等领域需要解决的关键问题之一,高精度的交通流预测对于缓解城市交通拥堵、避免社会资源浪费具有重要意义[1]。目前,建模预测短时交通流的方法很多[2],常见的模型有:历史平均模型、时间序列模型、卡尔曼滤波模型、神经网络模型等,其中历史平均模型原理简单、运算效率高,但预测精度低,应对突发交通状况的能力差,适用于静态的、对精度要求不高的交通流预测;时间序列模型实时性好、稳定性佳,但预测精度过于依赖样本数量,适用于交通流量波动幅度小的路段;卡尔曼滤波模型对稳态交通流的预测精度高,但预测精度依赖于交通流的线性特征,适用于线性非实时在线交通流预测;神经网络模型自适应学习能力强、实时性好、预测精度较高,但收敛速度慢,适用于复杂、多变、非线性的交通流预测。将小波分析与神经网络相结合的小波神经网络对非平稳信号具有良好的时频局部特性和变焦能力,且收敛速度比一般神经网络速度快,能够更好地实现对短期交通流的预测,因此本文运用小波神经网络理论建立预测模型,并对美国加州高速公路某单点的短时交通流进行预测[3, 4, 5, 6]。
目前,神经网络已被很多学者应用于短时交通流预测,如沈永增[7]的结合混沌粒子群算法和小波神经网络的模型、姚琛[8]的结合粗集和神经网络的模型、杨世监[9]的结合模糊C均值和神经网络的模型在短时交通流预测方面都取得较好的预测效果。他们大多考虑交通流的非线性特征,但较少考虑交通流的其他特性,如相似性。在利用交通流的相似性进行短时预测方面已有一些较出色的工作[10]。这里的相似性一般是指交通流在日、星期、月等尺度上的周期相似性规律,大多数工作都是基于以日为单位的相似性,较少见到基于长时间尺度衡量的相似性方面的工作。基于此,本文利用相似系数和波动系数分析交通流在星期尺度上的相似性,并建立小波神经网络模型进行短时交通流预测,对比常见的基于以日为单位衡量相似性的工作,发现我们的预测精度高。该结果不仅有助于训练样本的选取,还有助于进一步提高预测精度,为缓解城市交通拥堵提供有效依据。
1 相似性判据由于人们工作作息有周期性,故出行产生的交通流就存在以日、星期、月等为单位的周期规律性,即相邻几天或者不同周但同“星期几”的交通流就存在着一定程度上的相似性,一般情况采用下面两个系数[10]衡量其相似程度。
(1)相似系数
以d为单位,将每天k个交通流数据作为一个列向量li=[xi,x2,Λ,xk]T(i=1,2,3,…,n),则n天所有数据构成矩阵L=[l1,l2,l3,Λ,ln]。则相似系数S为各个向量两两间相关系数的平均值,其表达式为:

式中R为矩阵L的相关系数阵,其表达式为:
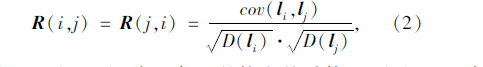
式中,cov(li,lj)为li与lj的协方差系数;D(li),D(lj)分别为li,lj的方差。S的值越大,表明相邻两天交通流的相似性越大。
(2)波动系数
令向量M=[E(l1),E(l2),Λ,E(ln)],即M的每个元素代表相应天的交通流均值。定义波动系数T为:
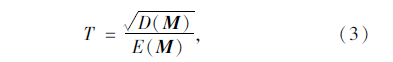
式中,D(M)为M的方差;E(M)为M的均值。T的值越小,表明各天交通总流量变化程度越小。
2 小波神经网络预测模型、算法和评价指标 2.1 小波神经网络预测模型小波神经网络(Wavelet Neural Network,WNN)是在小波分析理论基础上发展的一种新型前馈型神经网络,它兼具小波变换良好的时频局域化、变焦特性和神经网络的自学习能力,具有较强的非线性逼近能力和容错能力[7]。
小波神经网络实质上是由小波理论和神经网络结合产生的。目前被广泛应用的结合方式有两种: 松散型和融合型。本文采用融合型。
图1给出了小波神经网络的预测模型结构,即将神经网络和小波两者直接融合,将常规神经网络隐含层的传输函数用小波函数代替。输入层有n个神经元,隐含层有m个神经元,输出层有1个神经元;wij表示从输入层的第i个神经元到隐含层的第j个神经元之间的权值;w′jk表示从隐含层的第j个神经元到输出层的第k个神经元之间的权值;隐含层节点的传递函数h为小波基函数。隐含层选取的神经元激励函数为Morlet 小波函数,其表达式为:

|
| 图 1 小波神经网络预测模型 Fig. 1Wavelet neural network prediction model |

通过对式(4) 进行伸缩与平移变换,可以得到小波基函数,如式(5)所示。在输入信号序列为xi(i=1,2,3,…,k)时,其表达式为:

式中,oj为隐含层第j个节点的输出值;wij为输入层和隐含层的连接权值;bj为小波基函数的平移因子;aj为伸缩因子;h(·)为Morlet小波基函数。结合小波神经网络的理论知识,其输出量y为:

式中,w′jk为隐含层到输出层的的连接权值;m为隐含层节点个数。
2.2 预测算法采用梯度修正法修正小波神经网络的权值和小波基函数参数,从而使小波神经网络预测输出不断逼近期望输出。小波神经网络算法步骤如下:
(1)初始化网络参数。包括网络阈值、连接权值、小波函数的平移和尺度系数,并根据需要设置网络学习速率。
(2)样本分类。把事先准备好的样本数据分为训练样本和测试样本,训练样本用于训练网络,测试样本用于测试网络预测精度。
(3)预测输出。把训练样本输入网络,计算网络预测输出并计算其与期望输出的误差ε。
(4)权值修正。根据误差ε修正网络权值和小波基函数参数,使网络预测值逼近期望值。
(5)判断算法是否结束,若未结束,返回步骤3。
小波神经网络训练完成后,用测试样本对网络进行预测仿真并评价网络的性能。
2.3 评价指标目前从各个侧面全面反映出所用方法预测能力的常见误差评价指标有[11, 12]:
(1)平均相对误差

(2)均方误差百分比

(3)均等系数

式中,xi为预测输出;x′i为实际输出;n为样本个数;MRE和MSPE值越小,EC值越大,则模型的预测性能越好。
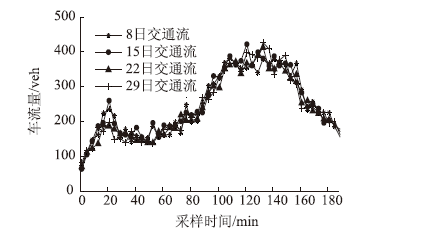
3 预测结果分析 3.1 相似性判断试验采用的交通流数据来源于美国加州高速公路通行能力度量系统(Caltrans Performance Measurement System,PeMS)数据中的某单点2014年4月6:00—23:00时段内的交通流数据,采样间隔为5 min。图2描述的是其4月26日~29日的以日为尺度的交通流,可以看出,4 d的交通流趋势相似,但曲线的拟合度较差。图3给出的是4月8日、15日、22日、29日的以星期为尺度的交通流,可以看出,曲线趋势一致,且曲线拟合度较好,说明不同时间尺度衡量的交通流的相似程度不同。

|
| 图 2 相邻4天的交通流 Fig. 2Traffic flows of 4 adjacent days |
|
| 图 3 四个星期二的交通流 Fig. 3Traffic flows of 4 adjacent Tuesdays |
表1给出了上述两组交通流的相似系数和波动系数,其中R1(26,27)表示第1组26日与27日交通流量的相关系数,S1为第1组数据的相似系数,T1为第1组的波动系数,以此类推。表中第1组任意两天交通流相关系数最高为0.947 4,其余都低于0.9,相似系数为0.845 1,波动系数为0.181 5;第2组任意两天交通流相关系数都大于0.95,相似系数为0.959 7,波动系数为0.012 8。可以看出,同“星期几”交通流的相似性远比相邻几天交通流的相似性大。
| 第1组 | 相关系数 | 第2组 | 相关系数 |
| R1(26,27) | 0.894 6 | R2(8,15) | 0.959 2 |
| R1(26,28) | 0.767 1 | R2(8,22) | 0.960 2 |
| R1(26,29) | 0.810 2 | R2(8,29) | 0.954 9 |
| R1(27,28) | 0.811 7 | R2(15,22) | 0.962 5 |
| R1(27,29) | 0.839 6 | R2(15,29) | 0.955 2 |
| R1(28,29) | 0.947 4 | R2(22,29) | 0.965 9 |
| S1 | 0.845 1 | S2 | 0.959 7 |
| T1 | 0.181 5 | T2 | 0.012 8 |
分别将两组数据作归一化处理。训练神经网络时,若k为当天某任意时刻,第1组试验将相邻前3天的k时刻和当天k-1,k-2,k-3时刻的交通流数据作为输入,当天k时刻的交通流数据作为目标输出。4月25日至28日交通流数据作为训练样本,4月26日至29日交通流数据作为测试样本,预测29日k时刻的交通流;第2组试验将相邻前3周同“星期几”k时刻和当天k-1,k-2,k-3时刻的交通流数据作为输入,当天k时刻的交通流数据作为目标输出。4月1日、8日、15日、22日交通流数据作为训练样本,4月8日、15日、22日、29日交通流数据作为测试样本,预测29日k时刻交通流。
由于隐含层神经元个数的确定直接关系到预测精度的高低,本文采用试凑法来确定隐含层神经元个数。经测试,当隐含层神经元个数为10时,网络的各项指标较好。确定好隐含层节点个数后,再设定输入节点数为6,输出节点数为1,学习效率为0.01,训练目标为0.001,最大训练次数为100 次。图4给出了第1组试验的预测结果,预测曲线和实际曲线趋势大体一致,曲线拟合度一般,绝对误差的绝对值大多低于100 veh,但大多高于50 veh,有个别点高于100 veh。图5给出了第2组试验的预测结果,预测曲线和实际曲线趋势基本相同,曲线拟合度较好,绝对误差的绝对值大多低于50,只有个别高于50。这两组试验的预测性能评价指标如表2所示,它对应星期二的预测分析。

|
| 图 4 第1组预测结和绝对误差 Fig. 4Prediction result and absolute error of 1st group |

|
| 图 5 第2组预测结果及绝对误差 Fig. 5Prediction result and absolute error of 2nd group |
为了使模型预测精度的结果更具说服力,表2中也给出了星期一至星期日的预测性能评价指标。可以看出,以相邻天作为训练样本的MRE,MSPE,EC的平均值分别为13.80%,3.71%,0.916 8;以相邻星期作为训练样本的MRE,MSPE,EC的平均值分别为8.55%,1.32%,0.951 6,后者的MRE,MSPE比前者低,后者的EC比前者高,说明后者预测精度比前者高。结合图4、图5和表2,可发现训练样本的选择对预测精度有很大影响,选取相似性较大的交通流序列作为小波神经网络的训练样本,可提高预测精度。
| 数据样本类型 | MRE/% | MSPE/% | EC | |
| 星期一 | 相邻星期 | 8.84 | 1.77 | 0.953 6 |
| 相邻天 | 20.26 | 6.24 | 0.817 7 | |
| 星期二 | 相邻星期 | 8.48 | 1.25 | 0.955 5 |
| 相邻天 | 15.21 | 2.31 | 0.917 7 | |
| 星期三 | 相邻星期 | 8.11 | 1.08 | 0.952 7 |
| 相邻天 | 11.53 | 2.46 | 0.936 7 | |
| 星期四 | 相邻星期 | 7.00 | 0.85 | 0.954 6 |
| 相邻天 | 10.06 | 2.00 | 0.934 5 | |
| 星期五 | 相邻同星期 | 8.47 | 1.18 | 0.954 2 |
| 相邻天 | 9.91 | 1.87 | 0.947 6 | |
| 星期六 | 相邻星期 | 9.21 | 1.47 | 0.945 0 |
| 相邻天 | 17.55 | 7.41 | 0.926 7 | |
| 星期日 | 相邻星期 | 9.72 | 1.64 | 0.945 5 |
| 相邻天 | 12.46 | 3.69 | 0.936 9 | |
| 平均值 | 相邻星期 | 8.55 | 1.32 | 0.951 6 |
| 相邻天 | 13.80 | 3.71 | 0.916 8 |
本文结合交通流相似性和小波神经网络理论,提出了基于相似性的短时交通流预测,运用相似系数和波动系数研究了美国加州高速公路某单点的交通流,发现交通流在星期尺度上的相似性大于日尺度的相似性,在此基础上,建立了小波神经网络模型。对比这两组不同尺度交通流数据作为训练样本的预测试验,发现前者在预测性能上优于后者,说明选取相似性较大的交通流作为训练样本,能够优化系统预测性能。因此,该方法不仅有助于训练样本的选取,还有助于进一步提高预测精度,具有一定的可行性。
| [1] | CHAN K Y, DILLON T S,SINGH J, et al. Neural-network-based Models for Short-term Traffic Flow Forecasting Using a Hybrid Exponential Smoothing and Levenberg-Marquardt Algorithm[J]. |
| [2] | 陆海亭,张宁,黄卫,等.短时交通流预测方法研究进展[J].交通运输工程与信息学报,2009,7(4):84-90. LU Hai-ting,ZHANG Ning,HUANG Wei,et al. Research Progress of Short Term Traffic Flow Prediction Methods[J]. Journal of Transportation Engineering and Information, 2009, 7(4): 84-90. |
| [3] | LINGRAS P J,SHARMA S C, GOPALAKRISHNAN S. Short-term Traffic Volume Forecasts: Existing and Future Research[C]// Proceedings of Canadian Society of Civil Engineers Annual Conference. Montreal: Canadian Society for Civil Engineering, 1999: 429-438. |
| [4] | YIN H G,WONG S C,XU J M,et al. Urban Traffic Flow Prediction Using a Fuzzy-neural Approach[J]. |
| [5] | STATHOPOULOS A,KARLAFTIS M G. A Multivariate State Space Approach for Urban Traffic Flow Modeling and Prediction[J]. |
| [6] | CLARK S. Traffic Prediction Using Multivariate Nonparametric Regression[J]. |
| [7] | 沈永增,闫纪如,王炜.基于混沌粒子群优化小波神经网络的短时交通流预测[J].计算机应用与软件,2014,31(6):84-90. SHEN Yong-zeng,YAN Ji-ru,WANG Wei. Short-time Traffic Flow Forecast Based on WNN Opitimised by CPSO[J]. Computer Applications and Software, 2014,31(6):84-90. |
| [8] | 姚琛,罗霞,范少伦 H,等.基于粗集和神经网络耦合的短时交通流预测[J].公路交通科技,2010,27(11):104-107. YAO Chen,LUO Xia, VAN ZUYLEN,et al. Short-term Traffic Flow Forecasting Based on Coupling of Rough Set and Neural Network[J]. Journal of Highway and Transportation Research and Development, 2010,27(11):104-107. |
| [9] | 杨世坚,贺国光.基于模糊C均值聚类和神经网络的短时交通流预测方法[J].系统工程,2004,22(8):83-86. YANG Shi-jian,HE Guo-guang. A Short-term Traffic Flow Forecasting Method Based on Combination of Fuzzy C-mean Clustering and Neural Network[J]. Systems Engineering, 2004,22(8):83-86. |
| [10] | 欧晓凌,裘刚,张毅,等.城市交通流信息相似性分析与研究[J].中南公路工程,2003,28(2):4-7. OU Xiao-ling,QIU Gang,ZHANG Yi,et al. Analysis of Similarity for Urban Traffic Volumes [J]. Central South Highway Engineering, 2003,28(2):4-7. |
| [11] | 王娇,李军.最小最大概率回归机在短时交通流预测中的应用[J].公路交通科技,2014,31(2):121-127. WANG Jiao,LI Jun. Application of Minimax Probability Machine Regression in Short-term Traffic Flow Prediction[J]. Journal of Highway and Transportation Research and Development, 2014,31(2):121-127. |
| [12] | 孙占全,潘景山,张赞军,等.基于主成分分析与支持向量机结合的交通流预测[J].公路交通科技,2009,26(5):127-131. SUN Zhan-quan,PAN Jing-shan,ZHANG Zan-jun,et al. Traffic Flow Forecast Based on Combining Principal Component Analysis with Support Vector Machine[J]. Journal of Highway and Transportation Research and Development, 2009,26(5):127-131. |
 2015, Vol. 32
2015, Vol. 32
