扩展功能
文章信息
- 韩雪, 刘英舜, 郭唐仪
- HAN Xue, LIU Ying-shun, GUO Tang-yi
- 城市轨道交通网络中断下的有效路径搜索模型
- A Valid Path Searching Model for Interrupted Urban Rail Transit Network
- 公路交通科技, 2015, Vol. 32 (10): 97-101
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 32 (10): 97-101
- 10.3969/j.issn.1002-0268.2015.10.016
-
文章历史
- 收稿日期:2014-11-26
城市轨道交通是指具有固定线路、铺设固定轨道、配备运输车辆及服务设施等的公共交通设施。近年来,随着我国城市轨道交通的迅速发展,北京、上海、广州、南京等城市的轨道交通已逐步由单线运营向网络化运营转变。然而,由于城市轨道交通网络复杂、指挥运营组织管理集中等特点,一旦发生线路中断,不仅会导致停运车站的乘客滞留,还会因轨道交通网络影响范围广而引起网络中各关联站点的乘客滞留。因此,在地铁线路中断时,能够合理地寻找到替代线路,实现城市轨道交通线路中断下的有效路径搜索就显得尤为重要。
有效路径求解算法是由R.B.Dial于1971年提出的,Dial有效路径[1]是指出行者选用的路径所包含的路段会使其越来越远离起点,且越来越靠近终点。此后,中外学者主要在对传统路径搜索方法进行改进或采用智能优化算法进行路径搜索方面进行了研究。李景等[2]针对现有有效路径搜索所存在的舍近求远、搜索结果与实际情况不符等缺点,引入量化指标对搜索方法进行改进,能够比较真实地反映出最短路径以及随机效用的影响作用。A. Lozano等[3]首次根据不同出行者的不同喜好来确定合理的出行路径,对多路径和可行路径的概念进行定义,为在网络中寻找最短的可行路径定义了一个标号方法。牛学琴等[4]在构建联合公交网的基础上利用Dijkstra算法搜索公交网络路径,进而采用广义费用效用模型完成公交线路的客流预测。
然而在建立公交网络时,文章假设可以满足网络中任意两点间的出行、乘车只选用步行或公交出行,因此存在一定的局限性。魏航等[5]结合Dijkstra与K短路方法求解双目标最短路问题。张小宁等[6]在对起讫点交通量调查的基础上提出了剩余最短路径算法。当确定起讫点间的最短路径后,将交通调查量转移到起讫点对上,从而解决了交通量重复或遗漏的问题。郝光等[7]综合K短路算法与多目标格序决策理论得出了多目标最短路径算法,能够更好地求解出现实生活中的有效路径集。在智能优化算法方面,侯立文[8]采用蚁群算法搜索有效路径进而进行交通分配。由于受到目标函数结构和目标个数的限定,传统的交通分配方法无法精确地模拟交通分配的实际情况。而基于仿生学的蚁群算法则很好地解决了多目标最短路的问题。李志纯等[9]针对交通分配中Dial有效路径、简单路径和有环路径之间的差别,讨论其有效路径搜索方法的不同特点,并进一步改进有效路径的定义,提出了一个用迭代过程求解确定性均衡分配的有效路径搜索算法。张波等[10]采用模拟退火算法解决TSP问题,模拟退火算法在解决NP问题时相对于传统的树形算法能够更准确地求解出最短路径,该方法在交通路径求解中得到了广泛应用。乐逸祥等[11]采用蚁群算法解决VRP问题,根据VRP问题的特点在传统蚁群算法的基础上进行时间窗约束、插点操作、动态改变挥发系数等改进,实现了货物配送路径优化。
目前,学者们在有效路径搜索的研究中主要是针对图论和出行者路径选择的角度方面,但关于城市轨道交通线路中断下列车调度调整方面的研究还较少,相关的理论基础研究还比较薄弱。因此,本文进行线路中断下城市轨道交通有效路径搜索的研究,以提高城市轨道交通系统的应急保障能力,减少灾害带来的损失,保障乘客的人身财产安全。
1 城市轨道交通路网模型城市轨道交通网络可表示为G=(V,E)的有向图,其中E表示网络中的线路,E=(e1,e2,…em),m为网络中线路数量;V表示网络中的各站点,V=(v1,v2,…,vn), n为车站的个数;vi为网络中第i个车站。设S为相邻站点间的区段,S=(s1,s2,…,sq), q为网络中区段的个数;L为网络中的线路,L=(l1,l2,…,lm); Lj为网络中第j条线路。
1.1 普通车站与线路的关系普通车站仅属于一条线路,因此普通车站Vi与线路Lj之间的关系可以表示为:若Vi∈Lj,则车站Vi所属线路LVi=Lj。因此城市轨道交通网络中n个普通车站所属线路集合的表示方法如下:
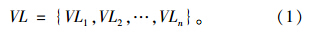
换乘车站作为多条线路的连接点,因此存在多个属于不同线路的前驱节点。设PVit为换乘站TVi在线路Lt上的前驱节点,用PVi表示该换乘车站前驱节点的集合如下:
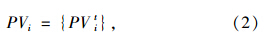

式中,Vit为换乘车站TVi在线路Lt上的前驱节点。若换乘站TVi为Lt的起点,则PVit=∅。
1.2.2 与后继节点的关系与前驱节点类似,换乘车站存在多个属于不同线路的后继节点。设SVit为换乘站SVi在线路Lt上的后继节点,则该换乘车站后继节点的集合SVi可表示为:

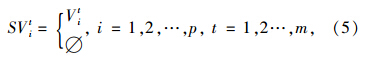
式中,Vit表示为换乘车站TVi在线路Lt上的后继节点。若换乘站TVi为Lt的终点,则SVit=∅。
1.3 区段与线路的关系每个区段都有特定线路与之相对应,即Si∈Lj。定义SLi表示区段Si所属线路,则有SLi=Lj。因此,轨道网络中q个区段所属线路的集合SLi可表示为:
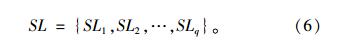
(4)线路之间的关系
两条线路相交可描述为线路Li与Lj存在节点Vi∈Lj,且Vj∈Li,数学模型表示为:
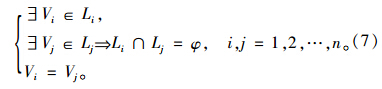
轨道交通线路中断,即轨道网络中存在故障点。故障点可广义地理解为网络中某节点或多节点的故障,某一区段或多个区段的故障,或某一范围内的区域故障。
若区段Si上存在故障点,且Si∈Li,Si仅存在唯一前驱节点SPi和后继节点SHi,即该区段不发生换乘行为,可直接将区段Si在轨道网路中删除,在路径搜索时将不会遍历到该区段,进而满足将区段Si设为故障点的约束条件。若故障点出现在节点Vi,其中Vi∈Li(i=1,2,…,n), 即Vi既可为普通节点也可为换乘节点。可在轨道网络中将节点Vi及所有与Vi相关联的区段Si全部删除,以实现Vi为故障点的条件约束。
2.1.2 换乘次数对有效路径的约束在以往的有效路径定义中,仅以路径不重复为约束条件,在实际应用过程中松散的约束条件会造成大量符合理论依据却不符合实际情况的冗余结果。换乘次数是乘客进行路径选择时最主要的考虑因素之一,其在乘客进行路径选择的决策过程中起着举足轻重的作用,因此将换乘次数引入有效路径的约束条件中可大大提高运算效率,有效地减少冗余。通过对上海地铁乘客进行问卷调查,结果表明59.73%的乘客能够接受的最大换乘次数为2次,26.99%的乘客可以接受3次换乘。
2.2 线路中断下的有效路径定义依据以上对于有效路径约束条件的分析,可将线路中断下的城市轨道交通网络有效路径定义如下:
设起讫点OD之间的第k条有效路径为PkOD,VkOD=(Vk1OD,Vk2OD,…,VknOD)为该有效路径上各节点的集合,SkOD=(Sk1OD,Sk2OD,…,SknOD)为组成该路径路段的集合;ckOD为k路径所需的广义费用;最小广义费用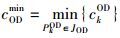 ,其中JOD表示OD间所有有效路径的集合;xk为k路径所需的换乘次数。则路径k需满足以下条件:
,其中JOD表示OD间所有有效路径的集合;xk为k路径所需的换乘次数。则路径k需满足以下条件:
(1) ∀SiOD,SjOD∈SkOD,SiOD≠SjOD;
(2) ∀ViOD,VjOD∈VkOD,ViOD≠VjOD;
(3) ∀ViOD,ViOD≠Va,其中Va为故障节点;
(4) ckOD≤cODmax(1+fmax(1)),且ckOD≤cODmin+fmax(2),fmax(1)≥0,fmax(2)≥0;
(5) xk≤Nmax,Nmax={2,3}。
条件(1)与条件(2)共同保证了有效路径中不存在区段和节点重复。条件(4)中引入相对系数fmax(1)和绝对系数fmax(2)两个概念,在以往的研究中认为在城市轨道交通网络中fmax(1)取0.2~1.8,fmax(2)取9~27较为合理。条件(5)则对轨道交通网络中的最大换乘次数进行限制,普遍认为换乘2~3次是乘客可以接受的。
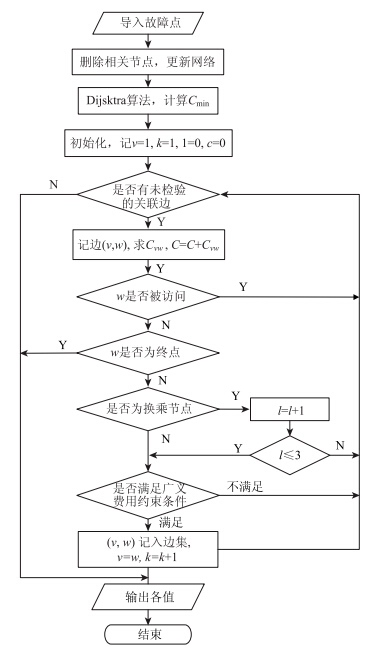
2.3 基于深度优先的城市轨道有效路径搜索算法在深度优先算法的基础上,结合线路中断下轨道交通网络的自身特点对城市轨道交通有效路径搜索算法做了以下改进:
(1)导入故障点,在图网中删除相应的节点和边,确定中断线路,更新图网数据。
(2)引入广义费用和换乘次数动态更新函数,即每将一条边划入有效路径集时,都会对目前路径所需广义费用及路径换乘次数进行判断。
改进后的有效路径搜索算法流程如下:
设开始搜索的顶点标号为1,S为有效路径区段集,以k为序号,v为正在检查的节点,w为待检查的节点,l为换乘次数,c为广义出行费用。
Step1:导入故障点,在网络中删除相关联的节点和边,更新网络。
Step2:采用Dijsktra算法计算OD间最短路径,计算最小广义费用cODmin。
Step3:初始化。记v=1,k=1,l=0,c=0。
Step4:寻找没有检验的关联边。
(1)取与v相关联的第1条没有被检验的边,设为(v,w),计算该边广义费用cvw,记c=c+cvw,转到下一步。
(2)若与顶点v相关联的边都被检验过,转到step8。
Step5:检验w是否被访问。
(1)若w是已被访问过的点,回到v,转到step4;
(2)若w是未被访问过的点,转到下一步;
Step6:节点类型判断。
(1)若w为终点D,转到step8;
(2)若w为普通节点,转到下一步;
(3)若w为换乘节点,l=l+1。如果l≤3,转到下一步,否则转到step4。
Step7:广义费用判断。
(1)若c≤cODmax(1+fmax(1)),且c≤cODmin+fmax(2),将(v,w)存入边集S,令v=w,k=k+1,转到step4;
(2)若不符合该条件,转到step4。
Step8:结束算法,输出各值。
算法流程如图 1所示。
|
| 图 1 基于深度优先的有效路径搜索算法流程图 Fig. 1Flowchart of valid path searching algorithm based on depth-first |
通过对上海轨道交通网络的数据调查,目前上海城市轨道交通中共有12条线路,287座车站(其中换乘车站34个),279个区段,线路间的换乘时间如表 1所示。
| L2 | L3 | L4 | L5 | L6 | L7 | L8 | L9 | L10 | L11 | L13 | |
| L1 | 1 | 5 | 5 | 1 | 9 | 1 | 1 | 3 | 9 | 9 | 9 |
| L2 | 1 | 1 | — | 3 | — | 5 | 1 | — | 5 | — | |
| L3 | 1 | — | 3 | 1 | 4 | 3 | 1 | 4 | 2 | ||
| L4 | 1 | 1 | 1 | 1 | 2 | 4 | 2 | ||||
| L6 | 1 | 1 | 1 | — | — | — | |||||
| L7 | 1 | 1 | — | — | — | ||||||
| L8 | 1 | 1 | — | — |
依据上一节有效路径算法流程的基本思想,采用面向对象的C#语言可对上海城市轨道交通网络有效路径搜索进行程序设计。以上海西站和浦东国际机场为起讫点,当人民广场站(换乘车站)发生线路中断时。将人民广场站设为故障点,设fmax(1)=0.4,fmax(2)=15,Nmax=3,可以搜索出5条符合条件的有效路径, 每条路径的换乘次数、途经站点、所需时间、所需费用等信息如表 2所示。
| 路径 |
换乘 次数 |
运行时 间/min |
费用/ 元 | 换乘站点 | 运行线路 |
| 1 | 2 | 79 | 7 | 曹杨路、世纪大道 | L11-L4-L2 |
| 2 | 3 | 88 | 7 |
曹杨路、上海火车 站、世纪大道 | L11-L3-L4-L2 |
| 3 | 3 | 93 | 7 |
曹杨路、宝山路、 世纪大道 | L11-L3-L4-L2 |
| 4 | 3 | 98 | 7 |
江苏路、静安寺、 龙阳路 | L11-L2-L7-L2 |
| 5 | 3 | 98 | 7 |
曹杨路、海伦路、 南京东路 | L11-L4-L10-L2 |
本文利用图论的基本原理对城市轨道交通线路中断下的路网结构和数据存储等方面进行了分析研究,并结合轨道交通线路中断的具体情况建立起路网模型,对网络中各节点、区段、线路间的相互关系进行了描述。
本文还依据线路中断下轨道交通网络的自身特点,引入故障点约束、广义费用约束、最大换乘次数约束等限制条件,对城市轨道交通网络线路中断下的有效路径进行了重新定义,进而提出了基于深度优先的有效路径搜索算法,并利用C#语言编写程序设计出城市轨道交通网络有效路径查询系统。该系统可以通过导入城市轨道交通网络信息和约束条件,实现满足各约束条件有效路径的搜索。
| [1] | DIAL R B. A Probabilistic Multi-path Traffic Assignment Model Which Obviates the Need for PATH Enumeration[J]. |
| [2] | 李景, 彭国雄, 臧亦文, 等. 改进型多路径分配模型及算法设计[J].系统工程理论与实践, 2001, 21(9):130-134. LI Jing, PENG Guo-xiong, ZANG Yi-wen, et al. An Improved Multi-path Assignment Model and Algorithms Design[J]. Systems Engineering-Theory & Practice, 2001, 21(9):130-134. |
| [3] | LOZANO A, STORCHI G. Shortest Viable Hyper Path in Multimodal Networks[J]. |
| [4] | 牛学勤, 王炜. 基于最短路搜索的多路径公交客流分配模型研究[J]. 东南大学学报: 自然科学版, 2002, 32(6):917-919. NIU Xue-qin, WANG Wei. Study on the Model of Transit Network Multi-path Assignment Based on Shortest Path Search[J]. Journal of Southeast University: Natural Science Edition, 2002, 32(6):917-919. |
| [5] | 魏航, 蒲云, 李军, 等. 一种求解双目标最短路的方法[J]. 系统工程, 2005, 23(7):113-117. WEI Hang, PU Yun, LI Jun, et al. An Approach to Biobjective Shortest Path[J]. Systems Engineering, 2005, 23(7):113-117. |
| [6] | 张小宁, 林航飞, 陈小鸿, 等. 剩余最短路径算法应用于起讫点交通调查统计[J]. 同济大学学报: 自然科学版, 2006, 34(10):1335-1339. ZHANG Xiao-ning, LIN Hang-fei, CHEN Xiao-hong, et al. An Application of Residual Shortest Route Algorithm in Traffic OD Survey[J]. Journal of Tongji University: Natural Science Edition, 2006, 34(10):1335-1339. |
| [7] | 郝光, 张殿业, 冯勋省, 等. 多目标最短路径模型及算法[J]. 西南交通大学学报, 2007, 42(5):641-646. HAO Guang, ZHANG Dian-ye, FENG Xun-sheng, et al. Model and Algorithm for Shortest Path of Multiple Objectives[J]. Journal of Southwest Jiaotong University, 2007, 42(5):641-646. |
| [8] | 侯立文, 蒋馥. 一种基于蚂蚁算法的交通分配方法及其应用[J]. 上海交通大学学报, 2001, 35(6):930-933. HOU Li-wen, JIANG Fu. Method of Traffic Allocation Based on Ant Algorithm and Its Application[J]. Journal of Shanghai Jiaotong University, 2001, 35(6):930-933. |
| [9] | 李志纯, 黄海军. 随机交通分配中有效路径的确定方法[J]. 交通运输系统工程与信息, 2003, 3(1):28-32. LI Zhi-chun, HUANG Hai-jun. Determining the Efficient Paths in Stochastic Traffic Assignment[J]. Journal of Transportation Systems Engineering and Information Technology, 2003, 3(1):28-32. |
| [10] | 张波, 叶家玮, 胡郁葱, 等. 模拟退火算法在路径优化问题中的应用[J]. 中国公路学报, 2004, 17(1):79-81. ZHANG Bo, YE Jia-wei, HU Yu-cong, et al. Application of Optimizing the Path by Simulated Annealing[J]. China Journal of Highway and Transport, 2004, 17(1):79-81. |
| [11] | 乐逸祥, 周磊山, 乐群星, 等. 求解物流配送路径优化问题的一种改进蚁群算法[J]. 计算机集成制造系统, 2006, 12(6):905-910. YUE Yi-xiang, ZHOU Lei-shan, YUE Qun-xing, et al. Improved Ant Colony Algorithm for Logistics Distribution Routing Problem[J]. Computer Integrated Manufacturing Systems, 2006, 12(6):905-910. |
 2015, Vol. 31
2015, Vol. 31
