扩展功能
文章信息
- 安朗, 张昕然
- AN Lang, ZHANG Xin-ran
- 整体吊装钢管混凝土系杆拱桥施工风险非线性模糊评判
- Nonlinear Fuzzy Evaluation of Construction Risk of Integral Hoisting CFST Tied Arch Bridge
- 公路交通科技, 2015, Vol. 31 (10): 91-96
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (10): 91-96
- 10.3969/j.issn.1002-0268.2015.10.015
-
文章历史
- 收稿日期: 2014-11-24
2. 西安市市政设施管理局, 陕西 西安 710016
2. Xi'an Municipal Facilities Authority, Xi'an Shaanxi 710016, China
桥梁工程由于建设环境复杂、施工技术难度大、不安全因素动态变化快以及主体从业人员流动性大等原因,多年来施工安全事故呈现易发、频发、多发等特点[1]。为预防重特大安全事故的发生,有效降低施工风险,交通运输部于2011年5月颁布《公路桥梁和隧道工程施工安全风险评估指南》(试行)(以下简称《指南》)规范全国桥梁施工风险评估工作,要求对施工过程中具有风险的大跨径桥梁、采用新材料和新工艺桥梁、特殊结构桥梁以及施工环境复杂、施工工艺复杂的桥梁进行风险评估[2]。常用的风险评估方法包括:模糊综合评判法、神经网络法、指标体系法、风险矩阵法、基于可靠度的结构失效概率求解法、蒙特卡洛模拟法等。各种方法有其自身的特点,鉴于桥梁施工风险影响因素的模糊性以及认识的局限性,模糊综合评判法在桥梁施工风险评估工作中得到广泛应用,但目前仍存在一定的局限和不足:其一,目前的赋权方法包括主观赋权法[3, 4](例如德尔菲法、层次分析法、模糊统计法等)和客观赋权法[5, 6](例如熵值法、均方差法、关联度分析法),主观赋权法客观性差但解释性强,客观赋权法一般情况下较为准确但有时与实际相悖,两类方法均存在优缺点,影响赋权精度[7];其二,现有的模糊综合评判均是基于线性加权,不能体现评判过程中的非线性特点[8]。因此,应完善原有的模糊评判方法,并将其运用在桥梁施工安全风险评估当中。
整体吊装钢管混凝土系杆拱桥是将钢管拱肋及劲性骨架装配成整体后吊装到设计桥位的施工方法,大幅缩短了封航时间,有良好的经济效益。但是,整体吊装法在国内应用较少,施工过程中存在较大的风险,本文针对整体吊装钢管混凝土系杆拱桥施工全过程,通过建立重视人员安全的层次评价体系,引入主观赋权法与客观赋权法相结合的结构熵权法,采用非线性模糊算子进行施工风险模糊评判,使桥梁施工风险评估方法更具合理性,为制订相应的施工安全风险控制措施奠定基础。
1 施工风险源识别桥梁施工安全风险评估首先应进行施工安全风险源识别,为保证风险源识别全面到位,又避免风险源过于繁杂,应依据施工工序进行识别,采用专家调查法辨识出风险较大的风险源,建立层次评价体系,作为施工风险评估的对象。
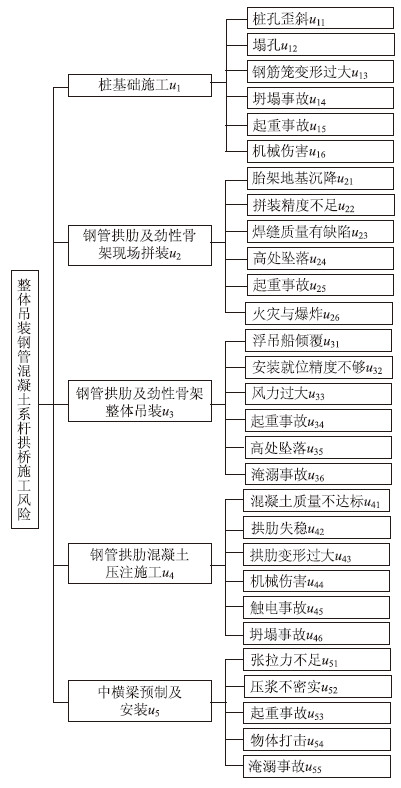
整体吊装钢管混凝土系杆拱桥的施工工序包括:桩基础施工、承台和桥墩施工、钢管拱肋及劲性骨架现场拼装、钢管拱肋及劲性骨架整体吊装、拱脚及端横梁混凝土浇注、钢管拱肋混凝土压注施工、系杆现浇混凝土、吊杆内成品索的安装及张拉、中横梁预制及安装、系杆预应力张拉、行车道板预制及安装、桥面系及附属工程等。经专家小组调查讨论,选取5项施工工序为重大风险源并作为二级风险因素。一级风险因素的选取遵循《指南》重视人员安全的原则,参照《企业职工伤亡事故分类标准》(GB 6441—86)中人员安全事故分类标准[9],同时考虑施工过程中的结构安全,根据各施工工序的不同特点,选取29项风险作为一级风险因素。基于整体吊装钢管混凝土系杆拱桥风险源识别结果,建立相应的层次评价体系,如图 1所示。图 1中的起重事故、坍塌事故、机械伤害、高处坠落、火灾与爆炸、淹溺事故、触电事故、物体打击均为人员安全事故,其余为结构安全事故。
|
| 图 1 整体吊装钢管混凝土系杆拱桥施工风险层次评价体系 Fig. 1 Integral hoisting CFST tied arch construction risk level evaluation system |
采用模糊评判方法进行整体吊装钢管混凝土系杆拱桥施工风险评估必须首先明确因素集U和评价集V[10],对应同一二级风险因素的一级风险因素组成一个因素集,所有二级风险因素组成一个因素集,评价集的构建参照《指南》中的风险等级,V={低度风险,中度风险,高度风险,极高风险}。根据模糊数学理论以及前述层次评价体系,整体吊装钢管混凝土系杆拱桥二级模糊评判计算模型为:
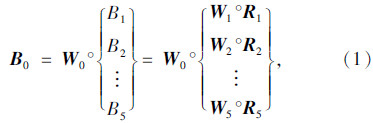
本文采用结构熵权法确定各级风险因素的权向量,结构熵权法基于熵理论,是一种将主观赋权法和客观赋权法相结合的方法[11],具体步骤如下:
(1)收集专家意见,形成典型排序。针对各因素集中的风险因素,采用德尔菲法收集专家对各风险因素的重要性排序意见,即确定同一个风险因素集中风险因素的重要性顺序。
(2)对典型排序进行熵值计算及盲度分析。专家的排序意见常因为数据噪声产生潜在的偏差和数据的不确定性,为减少数据噪声和不确定性,需采用熵值理论计算典型排序中数据的熵值。
设有k个专家参加咨询调查,则得到k种排序结果,每种结果对应的因素集记为{ai1,ai2,…,ain},由k种结果可得典型排序矩阵A(A=(aij)k×n,i=1,2,…,k,j=1,2,…,n),其中aij表示第i位专家对第k个因素的排序意见。
对上述典型排序进行定量转化,定义定性排序定量转化熵函数为:
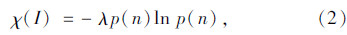
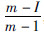 ,取λ=
,取λ=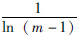 代入式(2)得:
代入式(2)得:
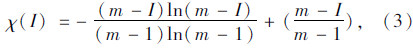
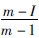 ,令:
,令:

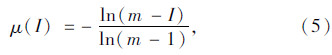
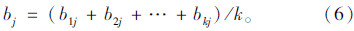
专家zj对因素uj由认知产生的不确定性称为认识盲度,记为Qj:
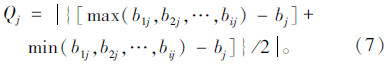
定义k位专家关于某一个因素uj的总体认识度为xj,
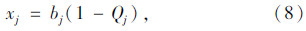
(3)归一化处理。为得到因素uj的权重,对xj进行归一化处理,αj=xj/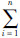 xj,W=(α1,α2,…,αn)即为风险因素集的权向量。
xj,W=(α1,α2,…,αn)即为风险因素集的权向量。
现有的桥梁施工风险模糊评判方法一般采用线性模糊算子进行运算,而桥梁施工过程涉及的风险因素众多,评判过程非线性特征明显,否则无法反映某一风险因素风险过大对整个评判过程的突出影响。因此,非线性模糊算子适用于桥梁施工风险评估,评判结果更加合理。
首先,定义评判因素突出影响程度系数向量Λ,记为Λ=(λ1,λ2,…,λn),其中λi≥1,因素ui(uij)对评判结果的突出影响程度越大,则λi越大。令λ=max{λ1,λ2,…,λn},定义模糊评判模型中非线性模糊算子为[4]:
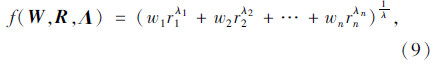

评判因素突出影响程度系数向量Λ应根据工程经验确定,风险因素影响越大,其评判结果从数值上看呈非线性增加,为反映此种规律,根据文献[13]中层次分析法多种标度的比较结果以及λi的取值原则,提出λi的计算公式:
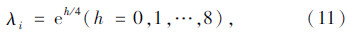
结构熵权法是主观赋权法与客观赋权法的结合,充分发挥了两类赋权方法的优势。采用德尔菲法收集专家意见,对风险因素进行典型排序,体现了主观赋权法的特征。熵作为不确定性程度的度量[14],定义熵函数作为定量转化函数,通过式(2)~式(5)的推导,表明了采用熵函数进行权重计算的有效性。针对熵函数计算结果进行认识盲度分析,消除了专家典型排序阶段对事物认识的不确定性,使专家意见具有一致性收敛,展现了结构熵权法在权重求取方面的独特优势。
非线性模糊评判算法是对传统模糊评判方法的改进,传统模糊评判方法采用的是线性加权,但大量评价实践工作证明,评价工作的不确定性导致了评价的非线性,仅靠增大权重无法体现某些因素对整个评判结果的突出影响。通过引入评判因素突出影响程度系数向量Λ并构造非线性模糊算子,实现了模糊评判的非线性,文献[8]对非线性模糊算子的科学性与合理性做了证明。本文根据桥梁施工经验以及层次分析法的标度特征提出的λi计算公式具有非线性特征,能较好地表示突出影响程度系数,适用于桥梁施工非线性模糊评判。
本文采用基于结构熵权法的非线性模糊评判方法,区别于以往桥梁施工风险评估方法。结构熵权法保证了权重向量求解的精度,非线性模糊评判则突出了评判过程的非线性特点,评判结果与桥梁施工实际风险更加接近。
3 工程应用金塔大桥位于金坛市开发区和白塔镇境内,横跨丹金溧漕河航道,桥梁与航道夹角78.65°,斜桥正做。金塔大桥主桥上部结构采用下承式钢管混凝土系杆拱,计算跨径96 m,矢跨比1/5,矢高19.2 m,拱轴线为二次抛物线,桥面宽30.1 m,设计荷载等级为公路-Ⅰ级。系梁采用箱形截面,拱肋采用哑铃形钢管混凝土,每片拱肋设16根刚性吊杆,风撑采用5道一字形钢管风撑,2道K字风撑,中横梁两侧设牛腿以支撑行车道板。金塔大桥主桥采用将已经拼装好的劲性骨架及钢管拱肋整体吊装至设计桥位的施工方法,是典型的整体吊装钢管混凝土系杆拱桥。
由于金塔大桥是典型的整体吊装钢管混凝土系杆拱桥,金塔大桥施工风险源识别结果以及相应的施工风险层次评价体系参见本文第2节内容。
针对金塔大桥进行施工风险评估,邀请12位专家,每4人分为一组,经过3轮,对各种风险因素的重要性进行排序,采用结构熵权法确定各级风险因素的权向量。钢管拱肋及劲性骨架整体吊装施工阶段对应的一级风险因素的典型排序结果及权向量计算见表 1。
| 风险因素 | u 31 | u 32 | u 33 | u 34 | u 35 | u 36 |
| 专家1组排序数 | 1 | 3 | 6 | 2 | 4 | 5 |
| 专家2组排序数 | 1 | 4 | 5 | 2 | 3 | 6 |
| 专家3组排序数 | 2 | 3 | 5 | 1 | 4 | 6 |
| 平均认识度b j | 0.974 | 0.789 | 0.495 | 0.947 | 0.750 | 0.426 |
| 认识盲度Q j | 0.014 | 0.020 | 0.035 | 0.014 | 0.020 | 0.035 |
| 总体认识度x j | 0.960 | 0.773 | 0.478 | 0.934 | 0.735 | 0.411 |
| 权重 | 0.224 | 0.180 | 0.111 | 0.218 | 0.171 | 0.096 |
采用上述方法计算可得5个二级风险因素及其各自所含一级风险因素权向量W0~W5,具体见表 2。
| 权向量 | 权向量值 |
| W 1 | {0.151,0.096,0.218,0.197,0.213,0.125} |
| W 2 | {0.141,0.224,0.218,0.180,0.140,0.097} |
| W 3 | {0.224,0.180,0.111,0.218,0.171,0.096} |
| W 4 | {0.216,0.162,0.223,0.179,0.125,0.095} |
| W 5 | {0.268,0.259,0.183,0.165,0.125} |
| W 0 | {0.255,0.195,0.264,0.124,0.162} |
根据工程项目的实际风险以及隶属度确定方法,可得钢管拱肋及劲性骨架整体吊装施工对应的一级风险因素的隶属度取值,见表 3,经过式(10)的变换可得模糊评判矩阵。由式(11)可得相应的评判因素突出影响程度系数λi,见表 4。通过表 2中的权向量以及式(9)计算可得钢管拱肋及劲性骨架整体吊装施工对应的一级模糊评判向量B3={0.023,0.294,0.477,0.206}。
| 隶属度 | 低风险 | 中度风险 | 高风险 | 极高风险 |
| u 31 | 0 | 0 | 0.75 | 0.25 |
| u 32 | 0 | 0.4 | 0.6 | 0 |
| u 33 | 0.2 | 0.8 | 0 | 0 |
| u 34 | 0 | 0 | 0.7 | 0.3 |
| u 35 | 0 | 0.5 | 0.5 | 0 |
| u 36 | 0 | 0 | 0.65 | 0.35 |
| 风险因素 | u 31 | u 32 | u 33 | u 34 | u 35 | u 36 |
| λ ij | 3.49 | 4.48 | 1.65 | 2.72 | 2.12 | 1.28 |
采用上述方法计算可得到其他一级模糊评判结果,再根据式(1)以及评判因素突出影响程度系数λi计算得到二级模糊评判结果,各级模糊评判结果见表 5。按照最大隶属度原则处理B0中的评价指标,可得金塔大桥施工风险为高度风险。
| 评判结果 | 评判结果集 |
| B 1 | {0.181,0.433,0.383,0.003} |
| B 2 | {0.107,0.341,0.366,0.186} |
| B 3 | {0.023,0.294,0.477,0.206} |
| B 4 | {0.184,0.256,0.424,0.136} |
| B 5 | {0.172,0.469,0.312,0.047} |
| B 0 | {0.030,0.292,0.473,0.205} |
考虑整体吊装钢管混凝土系杆拱桥施工风险影响因素的模糊性与层次性特征,引入非线性模糊数学理论,对整体吊装钢管混凝土系杆拱桥施工风险评判方法进行了深入研究,由此得出如下结论:
(1)基于施工工序对整体吊装钢管混凝土系杆拱桥施工风险源进行识别,针对重大风险源的识别过程同时考虑人员安全和结构安全,保证了风险源识别的全面性和有效性。
(2)建立的施工风险层次评价体系以及二级模糊评判计算模型能较全面反映各风险因素对整体吊装钢管混凝土系杆拱桥施工安全的影响,且能体现其重要程度的层次性。
(3)采用结构熵权法计算权重,达到了客观赋权法与主观赋权法的统一,提升了权值精度。运用非线性模糊算子进行模糊评判计算,反映了评判过程的非线性特征,可突出高风险因素对评判过程的影响,使评判结果更具合理性。
| [1] | 郑祖恩, 李智勇, 吴欣.基于模糊综合评判法的预应力混凝土连续梁桥悬臂浇筑施工风险评估[J].公路工程, 2013, 38(2):60-64. ZHENG Zu-en, LI Zhi-yong, WU Xin. Cantilever Irrigating Construction Risk Assessment of Prestressed Concrete Continuous Beam Bridge Based on Fuzzy Comprehensive Evaluation Method[J].Highway Engineering, 2013, 38(2):60-64. |
| [2] | 交通运输部. 公路桥梁和隧道工程施工安全风险评估指南(试行)[S].北京:交通运输部, 2011. Ministry of Transport. Bridge and Tunnel Construction Security Risk Assessment Guide (Trial)[S]. Beijing:Ministry of Transport, 2011. |
| [3] | 匡星, 白明洲, 王成亮, 等.基于模糊评价方法的隧道岩溶突水地质灾害综合预警方法[J].公路交通科技, 2010, 27(11):100-103. KUANG Xing, BAI Ming-zhou, WANG Cheng-liang, et al. Research of Comprehensive Warning of Water Inrush Hazards in Karst Tunnel Based on Fuzzy Evaluation Method[J]. Journal of Highway and Transportation Research and Development, 2010, 27(11):100-103. |
| [4] | 陈国华, 吴武生, 徐三元, 等.基于WBS-RBS与AHP的跨海桥梁工程施工HSE风险评价[J].中国安全科学学报, 2013, 23(9):51-57. CHEN Guo-hua, WU Wu-sheng, XU San-yuan, et al. Assessment HSE Risk of during Sea-crossing Bridges Project Construction Based on WBS-RBS and AHP[J]. China Safety Science Journal, 2013, 23(9):51-57. |
| [5] | 高雪磊.高速公路桥梁施工风险评估优化研究[D].西安:长安大学, 2012. GAO Xue-lei.Study on Optimization of Highway Bridge Construction Risk Assessment[D]. Xi'an:Chang'an University, 2005. |
| [6] | 邱菀华, 谷晓燕. 工程管理熵学及其应用[J].中国工程科学, 2011, 13(8):73-79. QIU Wan-hua, GU Xiao-yan. Engineering Management Entropy Research and its Applications[J]. Engineering Science, 2011, 13(8):73-79. |
| [7] | 程启月.评测指标权重确定的结构熵权法[J].系统工程理论与实践, 2010, 30(7):1225-1228. CHENG Qi-yue. Structure Entropy Weight Method to Confirm the Weight of Evaluating Index[J]. Systems Engineering-Theory & Practice, 2010, 30(7):1225-1228. |
| [8] | 张晓慧, 冯英俊.一种非线性模糊综合评价模型[J].系统工程理论与实践, 2005, 25(10):54-59. ZHANG Xiao-hui, FENG Ying-jun. A Nonlinear Fuzzy Comprehensive Assessment Model[J]. Systems Engineering-Theory & Practice, 2005, 25(10):54-59. |
| [9] | GB 6441-86, 企业职工伤亡事故分类标准[S]. GB 6441-86, The Classification for Casualty Accidents of Enterprise Staff and Workers[S]. |
| [10] | 方志耕, 刘思峰, 朱建军, 等.决策理论与方法[M].北京:科学出版社, 2009. FANG Zhi-geng, LIU Si-feng, ZHU Jian-jun, et al. Decision-making Theory and Method[M].Beijing:Science Press, 2009. |
| [11] | 石黎.基于结构熵权-灰关联的绿色供货商评价与选择研究[J].计算机应用研究, 2012, 29(3):923-926. SHI Li. Research on Evaluation and Selection of Green Supplier Based on Structure Entropy-grey Correlation[J]. Application Research of Computers, 2012, 29(3):923-926. |
| [12] | 曹文贵, 翟友成, 张永杰.新奥法隧道施工风险非线性模糊评判方法[J].土木工程学报, 2010, 43(7):105-112. CAO Wen-gui, ZHAI You-cheng, ZHANG Yong-jie. Nonlinear Fuzzy Judgment Method of Construction Risk for NATM Tunneling[J]. China Civil Engineering Journal, 2010, 43(7):105-112. |
| [13] | 骆正清, 杨善林.层次分析法中几种标度的比较[J].系统工程理论与实践, 2004, 24(9):51-60. LUO Zheng-qing, YANG Shan-lin. Comparative Study on Several Scales in AHP[J]. Systems Engineering-Theory & Practice, 2004, 24(9):51-60. |
| [14] | 蔡萌, 杜海峰, 任义科, 等.一种基于点和边差异性的网络结构熵[J].物理学报, 2011, 60(11):165-173. CAI Meng, DU Hai-feng, REN Yi-ke, et al. A New Network Structure Entropy Based Node Difference and Edge Difference[J]. Acta Physica Sinica, 2011, 60(11):165-173. |
 2015, Vol. 31
2015, Vol. 31
