扩展功能
文章信息
- 于天来, 黄巍
- YU Tian-lai, HUANG Wei
- 基于遗传算法的体外预应力钢丝绳加固RC梁抗剪承载力计算方法
- Calculation Method of Shear Bearing Capacity of RC Beam Strengthened with External Prestressing Steel Wire Ropes Based on Genetic Algorithm
- 公路交通科技, 2015, Vol. 31 (10): 82-90,96
- Journal of Highway and Transportation Research and Denelopment, 2015, Vol. 31 (10): 82-90,96
- 10.3969/j.issn.1002-0268.2015.10.014
-
文章历史
- 收稿日期: 2014-03-31
在既有桥梁中,梁端受剪破坏是一种常见的破坏形式,主要表现为主拉应力裂缝数量多,宽度超限,斜裂缝向跨中发展,严重影响结构的安全。造成受剪破坏的原因主要有抗剪承载力不足、材料性能退化、车辆超载等。目前,对抗剪能力加固,主要有粘贴钢板、粘贴高强复合材料、复合砂浆钢筋网加固、增大截面等加固方法[1, 2, 3, 4]。它们各有优点,但是局限性也十分明显。钢丝绳抗剪加固技术是一种新型的体外预应力加固技术,主要的加固工艺为:将钢丝绳固定在梁体外侧后,张拉钢丝绳至指定预紧力锚固,锚固后外喷一层聚合砂浆防腐。该项技术具有加固效果明显、操作简单、耐久性好等优点,最早由韩国的S.Y.Kim等人研究提出。该项加固技术在我国也有所应用,自2009年,论文作者所在的课题组通过19片梁的试验对钢丝绳抗剪加固技术进行了较为系统的研究。其中,文献[5]通过5根钢丝绳体外预应力抗剪加固的钢筋混凝土梁和2根对比梁的试验,研究了矩形梁体外钢丝绳的竖向布置和斜向布置、T形梁体外钢丝绳不同的锚固方式对试验梁抗剪加固效果的影响;文献[6]通过不同带载水平的钢丝绳体外预应力加固钢筋混凝土梁的试验,研究了带载水平对钢丝绳体外预应力加固的钢筋混凝土梁抗剪承载能力的影响,认为随带载水平的提高,加固梁的抗剪承载能力降低;文献[7]通过不同损伤度的钢丝绳体外预应力加固钢筋混凝土梁的试验,研究了原梁损伤度对钢丝绳体外预应力加固的钢筋混凝土梁抗剪承载能力的影响,认为总体上随原梁损伤度的增大,加固梁的抗剪承载能力降低;文献[8]利用22片梁的加固试验梁抗剪承载能力试验结果,基于拱-桁架理论研究了钢丝绳体外预应力加固的钢筋混凝土梁的抗剪承载能力的计算方法,但在当时限于不同损伤度及带载水平试验梁的数量有限,在承载能力计算公式中,未考虑加固时原损伤度及恒载带载水平对加固梁抗剪承载力的影响。而实际上,桥梁抗剪加固时,梁总是带有一定损伤。同时,一般也很难完全卸载,总是在一定恒载水平条件下进行加固的。因此,在加固梁的抗剪承载能力计算时,应考虑原梁损伤程度及恒载带载水平的影响,否则会过高地估计加固梁的抗剪承载能力。
本文在文献[5, 6, 7, 8]中的试验结果基础上,采用混凝土损伤理论采用ANSYS软件对加固梁进行仿真分析,共仿真分析了不同损伤度及带载水平梁45片,再加上原来的22片梁,样本总数为67片。然后,基于遗传算法对损伤度及带载水平对加固梁的抗剪承载能力影响系数进行了研究。最后,将遗传算法得到的损伤度及带载水平影响系数与统计分析的结果进行了对比分析,以验证遗传算法得到的影响系数的可靠性。
1 试验概况 1.1 试验设计试验梁为矩形梁,截面尺寸b×h=20 cm×40 cm,梁长300 cm,计算跨径280 cm。试验梁梁长300 cm,计算跨径为280 cm,横截面尺寸b×h=20 cm×40 cm。混凝土强度等级为C25,C30,C40。箍筋(构造筋)采用R235,直径为φ8;纵向受拉主筋采用HRB335,直径为φ12,φ16,φ20,φ22和φ25;架立钢筋采用R235,直径为φ10。设计的各试验梁的情况见表 1。
| 编号 | 剪跨比 | 原梁配筋率/% | 混凝土强度等级 | 原梁配箍率/% | 原梁损伤程度/% | 预应力布筋间距/mm | 预加力/MPa | 目的 |
| D1 | 1.3 | 2.0 | C30 | 0.35 | — | — | — | 基准梁 |
| B2 | 1.3 | 1.0 | C30 | 0.35 | 70-卸载 | 250 | 822 | 原梁配筋率的影响 |
| B3 | 1.3 | 1.5 | C30 | 0.35 | 70-卸载 | 250 | 822 | 原梁配筋率的影响 |
| B4 | 1.3 | 2.0 | C30 | 0.35 | 70-卸载 | 250 | 822 | 原梁配筋率、混凝土标号的影响 |
| B5 | 1.3 | 2.7 | C30 | 0.35 | 70-卸载 | 250 | 822 | 原梁配筋率的影响 |
| B6 | 1.3 | 2.0 | C25 | 0.35 | 70-卸载 | 250 | 822 | 混凝土标号的影响 |
| B7 | 1.3 | 2.0 | C40 | 0.35 | 70-卸载 | 250 | 822 | 混凝土标号的影响 |
| D2 | 2 | 2.0 | C30 | 0.35 | — | — | — | 基准梁 |
| B10 | 2 | 2.0 | C30 | 0.35 | 70-卸载 | 250 | 822 | 原梁配箍率、原梁损伤程度、布筋间距的影响 |
| B11 | 2 | 2.0 | C30 | 0.20 | 70-卸载 | 250 | 822 | 原梁配箍率的影响 |
| B12 | 2 | 2.0 | C30 | 0.50 | 70-卸载 | 250 | 822 | 原梁配箍率影响 |
| B13 | 2 | 2.0 | C30 | 0.35 | 50-卸载 | 250 | 822 | 原梁损伤程度的影响 |
| B14 | 2 | 2.0 | C30 | 0.35 | 80-卸载 | 250 | 822 | 原梁损伤程度的影响 |
| B15 | 2 | 2.0 | C30 | 0.35 | 60-卸载 | 250 | 822 | 原梁损伤程度的影响 |
| B16 | 2 | 2.0 | C30 | 0.35 | 70-卸载 | 150 | 822 | 预应力布筋间距的影响 |
| B17 | 2 | 2.0 | C30 | 0.35 | 70-卸载 | 200 | 822 | 预应力布筋间距影响 |
| B18 | 2 | 2.0 | C30 | 0.35 | 70-卸载 | 300 | 822 | 预应力布筋间距影响 |
| B19 | 2 | 2.0 | C30 | 0.35 | 60-不卸载 | 250 | 822 | 带载水平的影响 |
| B20 | 2 | 2.0 | C30 | 0.35 | 50-不卸载 | 250 | 822 | 带载水平的影响 |
| B21 | 2 | 2.0 | C30 | 0.35 | 70-不卸载 | 250 | 822 | 带载水平的影响 |
| D3 | 2.7 | 2.0 | C30 | 0.35 | — | — | — | 基准量 |
| BJ | 2 | 2.0 | C30 | 0.35 | 70-卸载 | 250 | 822 | 钢丝绳布置方式的影响 |
本次试验选取直径为φ4.8 mm钢丝绳,单根钢丝绳截面面积Aps=10.83 mm2,加固用钢丝绳的技术性能指标见表 2。试验梁的图纸配筋情况见文献[5, 6, 7, 8]。
| 钢丝种类 | 抗拉强度设计值 f pd/MPa | 弹性模量 E p/MPa |
| 镀锌软钢丝 | 1 397 | 120 000 |
裂缝封闭材料采用型号JN-F封口胶和JN-L低黏度灌封胶,具体的技术指标要求见表 3。
| 性能项目 | 性能指标 | |
| 胶体性能 | 抗拉强度 | ≥20 |
| 抗拉弹性模量 | ≥1 500 | |
| 抗压强度 | ≥50 | |
| 抗弯强度 | ≥30,且不得呈脆性破坏 | |
| 钢-钢拉伸抗剪强度标准值 | ≥10 |
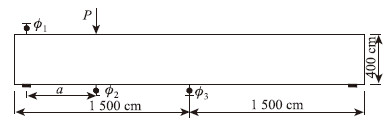
试验加载方式见图 1,施加荷载P试验使用油压千斤顶单点手动,基准梁单调分级加载至破坏,在接近开裂荷载和极限荷载时,适当地加密荷载分级。带载加固试验梁的加载过程主要分为3个阶段:预裂阶段、持荷加固阶段和加固梁试验阶段。在预裂阶段采用单调等级加载,加载至该梁的带载水平时,停止加载。然后维持荷载不变,对预裂的试验梁进行注胶处理,等待3 d之后待胶体强度达到要求以后再张拉竖向体外预应力筋进行加固处理。加固后,继续进行手动单点分级加载,当压力传感器的数据显示接近预测的加固梁的开裂荷载及加固后的极限荷载时,适当加密荷载分级;对于非带载梁,先加载至预压荷载,然后卸载至0,再修复裂缝,进行抗剪加固,重新加载至破坏。
|
| 图 1 加载方式及挠度测点布置图 Fig. 1 Loading mode and arrangement of deflection measuring points |
基准梁及加固试验梁的破坏形态均为剪压破坏模式。当试验荷载达到开裂荷载时,基准梁及加固梁开始出现斜裂缝。随着荷载的增大,斜裂缝长度及宽度逐渐增大,并形成一条主裂缝;当荷载接近极限荷载时,斜裂缝延伸至加载板下,直至斜裂缝顶端(剪压区)的混凝土被压碎而破坏。加固梁与基准梁的破坏形态未见差异,主要区别是加固梁的开裂荷载及极限荷载增大。在同级荷载作用下,裂缝宽度、箍筋应力及挠度减小。基准梁及加固梁破坏时的形态分别见图 2、图 3。

|
| 图 2 基准梁破坏特征 Fig. 2 Failure characteristics of reference beam |

|
| 图 3 加固梁破坏特征 Fig. 3 Failure characteristics of strengthened beam |
钢筋混凝土梁抗剪承载力的实质就是混凝土和其内钢筋共同抵制裂缝发展的过程。对于钢丝绳加固梁,钢丝绳可以从以下几个方面来提高梁的抗剪承载力:钢丝绳能限制和延缓裂缝向剪压区发展,使这部分混凝土能承担较大一部分外荷载;与裂缝相交的钢丝绳与体内的箍筋共同承受荷载,使纵向钢筋未出现撕裂破坏,从而使纵向钢筋的销栓作用得以更充分的发挥;钢丝绳限制裂缝的发展,从而提高骨料咬合力。因此,钢丝绳对抗剪承载力提高的作用机理与腹筋相似。
基准梁与各加固梁的加固前后的屈服荷载和极限荷载如表 4所示。表中数据表明,加固梁较基准梁的屈服荷载和极限荷载均有不同幅度的提高,提高最大值为60%和48.64%。
| 编号 | 试验值 | |||||
| 屈服荷载/kN | 提高值/% | 极限荷载/kN | 提高值/% | |||
| 加固前 | 加固后 | 加固前 | 加固后 | |||
| D1 | 300 | — | — | 370 | — | — |
| B1 | — | 460 | 53.33 | 530 | 43.24 | |
| B2 | — | 320 | 6.67 | — | 420 | 13.51 |
| B3 | — | 400 | 33.33 | — | 450 | 21.62 |
| B4 | — | 420 | 40 | — | 490 | 32.43 |
| B5 | — | 480 | 60 | — | 550 | 48.64 |
| B6 | — | 380 | 26.67 | — | 450 | 21.62 |
| B7 | — | 420 | 40 | — | 520 | 40.54 |
因损伤度梁及带载水平试验梁的试验样本有限,为扩大分析样本,采用非线性有限元方法增加损伤度及带载水平梁的样本。
2.1 有限元计算模型利用ANSYS有限元分析软件进行分析,在模拟分析中,其中基本假设为:梁体混凝土采用SOLID65单元模拟;支座和加载垫块采用SOLID45单元;体外筋和箍筋采用LINK8单元;采用等效荷载法实现预应力的施加;混凝土的本构关系采用我国《混凝土结构设计规范》(GB 50010—2010)中提出混凝土单向受压的应力-应变关系;破坏准则采用WILLAM-WARKE五参数混凝土准则;钢筋采用双折线模型,考虑钢筋强化[9, 10]。
当εc≤ε0时:
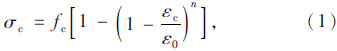

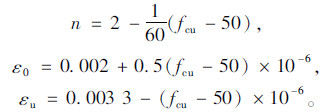
混凝土单元划分为20 mm单元网格,钢筋划分为20 mm单元网格;求解方法采用增量法,收敛精度取0.035。
2.2 模拟试验梁为扩大分析样本,本文在试验梁的基础上,设计了6组共45个有限元计算模型,每组模型都单独改变某一影响因素参数,其他设计因素不变,例如研究带载水平对承载力的影响时,带载水平设计从0到85%的10个等级,而其他如损伤度、配箍率、混凝土强度等级、体外筋间距等设计参数保持不变,共设计10个仿真模型,通过计算分析来研究带载水平对极限承载力的影响。模型具体设计参数见表 5。
| 研究目的 | 梁的设计参数 | 模型数量 | |||||
| 带载水平/% | 损伤度/% | 配箍率/% | 配筋率/% | 混凝土强度 | 体外筋间距/mm | ||
| 带载水平对承载力的影响 | 0,10,20,30,40,50,60,70,80,85 | 70 | 0.35 | 2.0 | C30 | 250 | 10 |
| 原梁损伤程度对承载力的影响 | 0 | 0,10,20,30,40,50,60,70,80,85 | 0.35 | 2.0 | C30 | 250 | 10 |
| 配箍率对承载力的影响 | 0 | 70 | 0.2,0.25,0.3,0.35,0.4,0.45,0.5,0.55,0.6 | 2.0 | C30 | 250 | 9 |
| 配筋率对承载力的影响 | 0 | 70 | 0.35 | 1.0,1.5,1.7,2.0,2.3,2.7 | C30 | 250 | 6 |
| 混凝土强度对承载力的影响 | 0 | 70 | 0.35 | 2.0 | C25,C30,C35,C40 | 250 | 4 |
| 体外筋间距对承载力的影响 | 0 | 70 | 0.35 | 2.0 | C30 | 100,150,200,250,300,350 | 6 |
采用9根加固梁的试验结果对有限元模型进行了验证,结果表明有限元模型计算的屈服荷载、极限荷载试验数据吻合良好,所有试件的模拟极限荷载误差在10%以内,对比情况见表 6。数据表明仿真模型是有效的,扩大的样本数可作为试验梁进行分析。
| 梁编号 | 屈服荷载/kN | 误差/% | 极限荷载/kN | 误差/% | ||
| 试验值 | 有限元计算值 | 试验值 | 有限元计算值 | |||
| B2 | 320 | 300 | 6.25 | 420 | 395 | 5.95 |
| B3 | 400 | 380 | 5 | 450 | 410 | 8.89 |
| B4 | 420 | 405 | 3.57 | 490 | 460 | 6.12 |
| B5 | 480 | 465 | 3.13 | 550 | 560 | 1.8 |
| B6 | 380 | 360 | 5.26 | 490 | 450 | 8.16 |
| B7 | 420 | 400 | 5.27 | 520 | 525 | 0.96 |
| B10 | 360 | 350 | 2.28 | 450 | 450 | 0 |
| B11 | 340 | 330 | 2.94 | 400 | 370 | 7.5 |
| B12 | 380 | 350 | 7.89 | 440 | 435 | 1.13 |
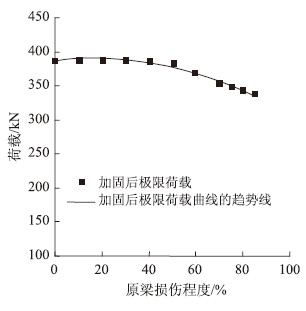
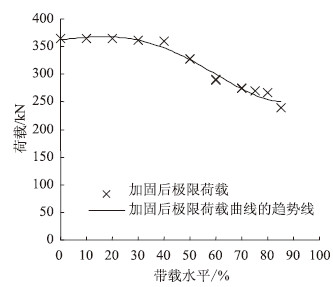
图 4为损伤度对加固梁抗剪承载力的影响,当损伤在50%以内时,加固梁的极限承载力变化不大;当损伤大于50%时,承载力随着损伤程度的增加而减小。图 5为带载水平对加固梁抗剪承载力的影响,随着带载水平的增大,加固梁的抗剪承载能力逐步减小,即加固效果的提高程度逐渐降低。
|
| 图 4 损伤度对加固梁抗剪承载力的影响 Fig. 4 Influence of damage degree on shear bearing capacity of strengthened beams |
|
| 图 5 带载水平对加固梁抗剪承载力的影响 Fig. 5 Influence of load level on shear bearing capacity of strengthened beams |
根据钢丝绳加固梁抗剪破坏机理,参照文献[7, 13],钢丝绳加固钢筋混凝土梁的抗剪承载能力可采用拱-桁架模型来计算,加固梁的纵向受拉钢筋相当于下弦拉杆,箍筋和钢丝绳为受拉腹杆,混凝土相当于受压斜腹杆。
(1)桁架模型
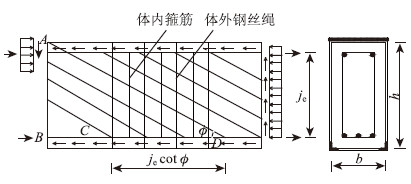
桁架模型的计算简图以及加固模式见图 6、图 7。
|
| 图 6 桁架模型及加固模式简图 Fig. 6 Schematic diagram of truss model and reinforcement model |
|
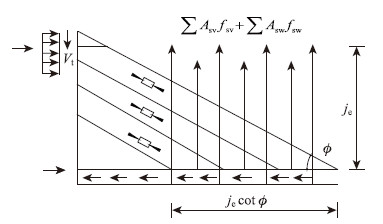
| 图 7 桁架模型的剪力平衡图 Fig. 7 Shear equilibrium diagram of truss model |
桁架模型所承担的抗剪强度为:
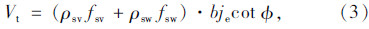
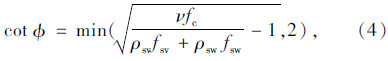
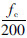 。
。
(2)拱模型
因为按照桁架模型建立的抗剪强度,随着配筋率的减小而降低,当无箍筋时抗剪强度为0,所以引入拱模型的概念,为了简化计算,将实际拱模型视为斜压杆,计算模式如图 8所示。
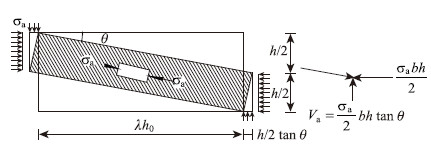
|
| 图 8 拱模型计算简图 Fig. 8 Calculation diagram of arch model |
由平衡条件得到拱模型中混凝土所承担的抗剪承载力为:
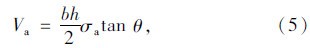
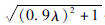 -0.9λ。
-0.9λ。
(3)拱-桁架模型
加固梁的抗剪承载力由桁架作用和拱作用叠加,计算公式为:
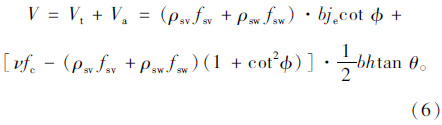
经对16个测点体外钢丝绳达到充分发展时的抗拉强度与设计强度对比发现,体外钢丝绳实际抗拉强度均达到或略高于设计值,利用统计分析取保证率为95%时,求得置信区间为1.125 5~1.214 5。理论上,设计强度可适当提高,但从安全及与规范相统一的角度,钢丝绳强度发挥系数应取1.0,即η1=1.0;在加固试验中,混凝土的带载水平和损伤程度对加固梁的承载力有明显影响,计算公式中引入带载水平和损伤程度的抗剪承载力因素。假设η2为混凝土的损伤调整系数,η3为混凝土的带载水平调整系数,加固梁抗剪承载力最终公式为:
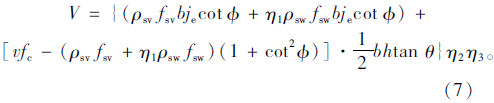
遗传算法是模拟达尔文的遗传选择和自然淘汰的生物进化过程的仿生计算方法,它用数学方法模拟了生物物种在繁衍生息的过程中优胜劣汰的遗传进化过程,将对问题的求解转化为对一群“染色体”(一般用二进制码串表示)的一系列操作,通过群体的进化,最后收敛到一个最适应环境的染色体上,从而实现在问题中搜索寻求最优解的目的。与其他优化方法比较,遗传算法不需要其他导数、空间知识等工具,直接以影响搜索方向的目标函数和相应的适应度函数为搜索信息,使用概率搜索方法在解空间内进行直接、充分、多点搜索信息并进行优化分析,具有鲁棒性强、全局搜索性强等特点,被广泛运用到工程技术优化应用中[11, 12]。
(1)数据样本的选择
利用遗传算法,确定η2为损伤调整系数、η3为带载水平系数时,首先应选择样本。分析η2时,试验梁样本在裸梁状态下损伤度为0,10%~85%,共14个样本,分为3组,损伤度分别为0~50%,50%~70%,70%~85%;分析η3时,选择损伤70%(典型状态)下,带载水平为裸梁、10%~85%,共14个样本,分为3组,带载水平分别为0~40%,40%~70%,70%~85%,数据样本见表 7。
| 分析裸梁状态下损伤系数 η2 | 分析损伤70%状态下带载系数η3 | ||||||
| 序号 | 梁号(模型编号) | 损伤度/% | 极限承载力/kN | 序号 | 梁号(模型编号) | 带载/% | 极限承载力/kN |
| 1 | Model1 | 0 | 389 | 15 | Model12 | 裸梁 | 365 |
| 2 | Model2 | 10 | 389 | 16 | Model13 | 10 | 364 |
| 3 | Model3 | 20 | 389 | 17 | Model14 | 20 | 364 |
| 4 | Model4 | 30 | 388 | 18 | Model15 | 30 | 362 |
| 5 | Model5 | 40 | 387 | 19 | Model16 | 40 | 360 |
| 6 | Model6 | 50 | 386 | 20 | B20 | 50 | 328 |
| 7 | B15 | 60 | 370 | 21 | Model17 | 50 | 327 |
| 8 | Model7 | 60 | 368 | 22 | B19 | 60 | 290 |
| 9 | B16 | 70 | 353 | 23 | Model18 | 60 | 289 |
| 10 | Model8 | 70 | 354 | 24 | B21 | 70 | 275 |
| 11 | Model9 | 75 | 348 | 25 | Model19 | 70 | 274 |
| 12 | B14 | 80 | 344 | 26 | Model20 | 75 | 270 |
| 13 | Model10 | 80 | 343 | 27 | Model21 | 80 | 266 |
| 14 | Model11 | 85 | 340 | 28 | Model22 | 85 | 260 |
(2)遗传算法的实现
确定适应度函数公式为:
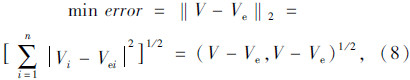
在遗传分析中,遗传算法的种群数量为100;交叉概率为0.8;变异概率为0.1;最大遗传代数为500;计算精度为1e-100。
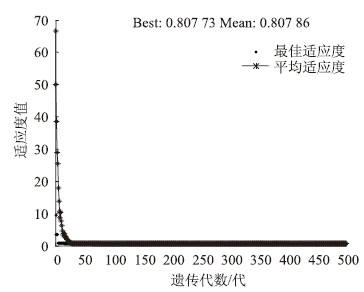
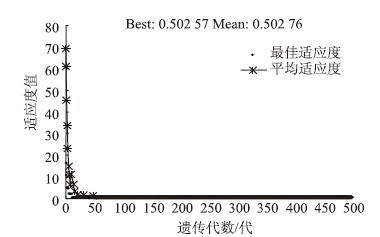
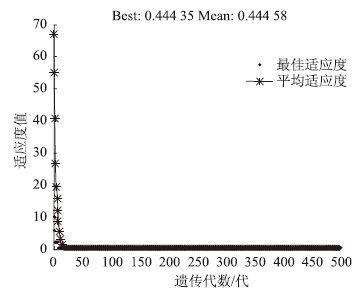
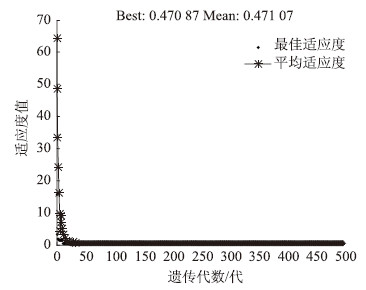
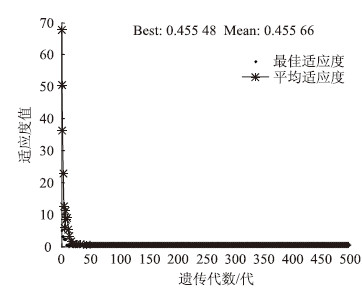
采用MATLAB的GA遗传算法模块,轮盘赌法计算选择概率,各组进行寻优。搜索过程如图 9~图 14所示,适应度的最终值分别为5.231 7×10-6,7.160 8×10-7,7.969 7×10-3,2.582 5×10-6,9.461 3×10-6,5.885×10-6,说明构造的计算适应度公式可以较好地逼近样本数据,满足收敛精度要求[14]。
|
| 图 9 裸梁损伤在50%以内的适应度函数变化曲线 Fig. 9 Adaptation function curve of bare beam with damage less than 50% |
|
| 图 10 裸梁损伤在50%~70%的适应度函数变化曲线 Fig. 10 Adaptation function curve of bare beam with damage within 50%-70% |
|
| 图 11 裸梁损伤大于70%的适应度函数变化曲线 Fig. 11 Adaptation function curve of bare beam with damage greater than 70% |
|
| 图 12 损伤70%且带载0~40%的梁的适应度函数变化曲线 Fig. 12 Adaptation function curve of beam with damage of 70% and load within 0-40% |
|
| 图 13 损伤70%且带载40%~70%的适应度函数变化曲线 Fig. 13 Adaptation function curve of beam with damage of 70% and load within 40%-70% |
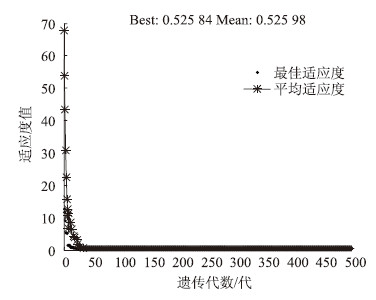
|
| 图 14 损伤70%且带载70%~85%的适应度函数变化曲线 Fig. 14 Adaptation function curve of beam with damage of injury in 70% and load within 70%-85% |
经遗传分析得出不同带载水平和损伤程度区间的调整系数,如表 8所示。在裸梁的状态下,损伤程度在50%以下时,损伤对加固梁抗剪承载力影响很小,损伤程度调整系数η2取1.0;损伤程度在50%~70%之间时,损伤程度调整系数η2均取0.9;损伤程度在70%以上时,损伤程度调整系数η2均取0.88。
| 影响因素 | 损伤度水平/% | ||
| 0~50 | 50~70 | 70~85 | |
| 裸梁状态下损伤调整系数 η 2 | 1.0 | 0.9 | 0.88 |
| 影响因素 | 带载水平/% | ||
| 0~40 | 40~70 | 70~85 | |
| 损伤70%状态下带载水平调整系数 η 3 | 1.0 | 0.87 | 0.85 |
在损伤70%状态下,带载水平在40%以下时,η3取1.0;带载水平在40%~70%之间时,η3均取0.85;带载水平在70%以上时,η3均取0.85。
3.5 遗传算法结果的可靠性分析为分析遗传算法确定的损伤系数和带载系数的可靠性,假定带载水平与损伤水平是独立的,互不影响。对各损伤度组及各带载水平组的样本进行统计分析,取统计均值加二倍的方差做为统计分析结果,统计结果的保证率达95%。分析结果见表 9。表中结果表明,遗传算法确定的损伤系数、带载水平系数与统计法确定95%保证率值十分接近,且等于或略大于统计值,说明遗传算法确定的损伤系数和带载系数是安全可行的。
| 影响因素 | 损伤度水平/% | |||||
| 0~50 | 50~70 | 70~85 | ||||
| 裸梁状态下损伤调整系数η 2 | 遗传 | 统计 | 遗传 | 统计 | 遗传 | 统计 |
| 1.0 | 0.99 | 0.9 | 0.88 | 0.88 | 0.87 | |
| 影响因素 | 带载水平/% | |||||
| 0~40 | 40~70 | 70~85 | ||||
| 损伤70%状态下带载水平调整系数 η 3 | 遗传 | 统计 | 遗传 | 统计 | 遗传 | 统计 |
| 1.0 | 1 | 0.87 | 0.82 | 0.85 | 0.73 | |
通过本文对体外预应力钢丝绳加固钢筋混凝土抗剪性能的研究,得出以下结论:
(1)揭示钢丝绳体外预应力加固钢筋混凝土梁的抗剪破坏机理,其抗剪能力可按拱-桁架模式计算。
(2)研究了损伤度及带载水平对的影响。当损伤在50%以内时,加固梁的极限承载力变化不大;当损伤大于50%时,承载力随着损伤程度的增加而减小;当带载水平在40%以内时,对加固梁的极限承载力影响不大;但当带载水平大于40%时,随带载水平的增大,加固梁的抗剪承载能力逐步减小,即加固效果的提高程度逐渐降低。
(3)给出了加固梁抗剪承载能力的损伤系数和带载水平系数η2,η3。在裸梁的状态下,损伤程度在50%以下时,损伤对加固梁抗剪承载力影响很小,损伤程度调整系数η2取1.0;损伤程度在50%~70%之间时,损伤程度调整系数η3均取0.9;损伤程度在70%以上时,损伤程度调整系数η3均取0.88。在损伤70%状态下,带载水平在40%以下时,η3取1.0;带载水平在40%~70%之间时,η2均取0.87;带载水平在70%以上时,η3均取0.85。
(4)遗传算法确定的损伤系数、带载水平系数与统计法确定95%保证率值十分接近,且等于或略大于统计值,说明遗传算法确定的损伤系数和带载系数是安全可行的。
| [1] | 罗利波.高性能复合砂浆钢筋网抗剪加固混凝土梁试验研究[J].建筑科学, 2013, 29(5):52-55. LUO Li-bo. Experimental Research on Shear Strengthening of RC Beams with HPFL[J]. Building Science, 2013, 29(5):52-55. |
| [2] | 杨军民, 郭子雄, 黄群贤.预应力钢丝绳箍加固钢筋混凝土梁抗剪承载力计算方法[J].华侨大学学报:自然科学版, 2011, 32(4):422-426. YANG Jun-min, GUO Zi-xiong, HUANG Qun-xian. Method for Calculating Shear Capacity of RC Beams Strengthened with Prestressed Wire Stirrups[J]. Journal of Huaqiao University: Natural Science Edition, 2011, 32(4):422-426. |
| [3] | 王景全, 戚家南. 有腹筋与无腹筋钢筋混凝土梁抗剪承载力统一计算方法[J]. 土木工程学报, 2013, 46(7):47-57. WANG Jing-quan, QI Jia-nan. Unified Shear Strength Computation Model for Reinforced Concrete Beams with and without Stirrups[J].China Civil Engineering Journal, 2013, 46(7):47-57. |
| [4] | 金锐光. PUFA材料用于钢筋混凝土梁抗剪加固的试验研究与理论分析[D].哈尔滨: 哈尔滨工业大学, 2013. JIN Rui-guang. Experimental Study and Theoretical Analysis of PUFA Material for Shear Strengthening in Reinforced Concrete Beams[D]. Harbin: Harbin Institute of Technology, 2013. |
| [5] | 于天来, 史伟卓, 于国语, 等.钢丝绳布置方式对抗剪加固性能影响的试验研究[J].武汉理工大学学报, 2012, 34(8):113-118. YU Tian-lai, SHI Wei-zhuo, YU Guo-yu, et al. Experimental Study on the Influence of Wire Rope Arrangement with the Shear Strengthening[J].Journal of Wuhan University of Technology, 2012, 34(8):113-118. |
| [6] | YU Tian-lai, TIAN Lei-lei, MA Qiang. The Shear Resistant Effect of RC Beam Strengthened with SWR External Prestressing under Dead Load Level when Strengthening[C]//Advanced Materials Research. Zurich, Switzerland: Trans Tech Publications, 2011:5576-5581. |
| [7] | 于天来, 侯宪斌, 田蕾蕾.原梁斜裂缝宽度对钢丝绳体外预应力抗剪加固效果的影响[D].哈尔滨:东北林业大学, 2012. YU Tian-lai, HOU Xian-bin, TIAN Lei-lei. Influence of Cracking Width of Original Beam on Shear Resistant Effect of RC Beam Strengthened with SWR External Prestressing[D]. Harbin: Northeast Forestry University, 2012. |
| [8] | YU Tian-lai, MA-Qiang, TIAN Lei-lei.The Ultimate Shear Bearing Capacity of RC Beam Strengthened with SWR External Prestressing[C]//Advanced Materials Research. Zurich, Switzerland: Trans Tech Publications, 2011:5571-5575. |
| [9] | 袁超, 张涛, 孙留颖. 基于ANSYS的钢筋混凝土桥梁结构有限元分析[J]. 山西建筑, 2014, 40(21):158-159. YUAN Chao, ZHANG Tao, SUN Liu-ying. Finite Element Analysis of Reinforced Concrete Bridge Structure Based on ANSYS[J]. Shanxi Architecture, 2014, 40(21):158-159. |
| [10] | 王新敏. ANSYS工程结构数值分析[M].北京:人民交通出版社, 2007. WANG Xin-min. Numerical Analysis of Engineering Structure by ANSYS[M].Beijing: China Communi-cations Press, 2007. |
| [11] | 汤迎红, 刘忠伟.MATLAB基础知识及工程应用[M].北京:国防工业出版社, 2014:137-151. TANG Ying-hong, LIU Zhong-wei. Basic Knowledge of MATLAB and Its Application in Engineering[M]. Beijing: National Defence Industry Press, 2014:137-151. |
| [12] | 盛仲飙. 遗传算法在函数优化中的应用[J]. 渭南师范学院学报, 2013, 28(2):17-19. SHENG Zhong-biao. Application of Genetic Algorithm in Function Optimization[J].Journal of Weinan Normal University, 2013, 28(2):17-19. |
| [13] | 贾平一, 李延涛, 王立军.基于桁架拱模型的抗剪承载力计算方法[J].河北建筑工程学报, 2001, 19(1):7-9. JIA Ping-yi, LI Yan-tao, WANG Li-jun. Calculation Methods of Shear Strength on Truss-arch Model[J].Journal of Hebei Institute of Architectural Engineering, 2001, 19(1):7-9. |
| [14] | 黄巍. 体外预应力钢丝绳加固RC梁受剪性能的研究[D]. 哈尔滨:东北林业大学, 2014:35-38. HUANG Wei. Research on Shear Behavior of RC Beams Strengthened with External Prestressing Steel Wire Rope[D]. Harbin: Northeast Forestry University, 2014:35-38. |
 2015, Vol. 31
2015, Vol. 31
